直接法框架下的模态灵敏度算法的研究进展

王 娜，黄 威，于 澜

(1.长春工程学院教务处，长春 130012； 2.吉林省公安厅网络安全保卫总队，长春 130005；3.长春工程学院理学院，长春 130012)

0 引言

自1965年发展至今，有关对称系统实或复模态向量一阶导数的计算无论从算法[1-3]到应用都已相当成熟，相应的模态向量的一阶泰勒展开式也随之得到发展和应用。但非对称系统的实或复模态向量的一阶及二阶导数问题一直没有很好的解决方案[4]。针对模态的灵敏度分析算法大致可分成直接法、代数法和模态法3种类型。3类方法都需对动力特征方程求导后得到灵敏度支配方程，它的系数矩阵至少降一个秩，这是由系统的特征值是否是重复的以及重特征值的重数来决定的[5]。直接法是对支配方程的系数矩阵进行非奇异化处理，从而直接求解模态灵敏度。代数法是把灵敏度支配方程与规范化条件方程求导后的方程联立，化为代数方程组，其未知向量由频率灵敏度和模态灵敏度联合构成，通过解方程组来同时求得频率及模态灵敏度。模态法是指首先构建完全的特征空间基底，在灵敏度支配方程中将模态灵敏度表示成全部基底的某一线性组合形式，最后利用各种方法来计算组合系数，从而确定模态灵敏度。目前的研究显示，系统特征对灵敏度分析必须与特征向量的规范正交化条件相关联[6-7]。

1 处理单频问题的Nelson算法与ojalvo算法

如果说，Nelson算法是将特征向量导数的灵敏度分成两部分，还需依赖特征向量所满足的规范化条件求那个特殊的线性组合系数，而Ojalvo算法不需求解那个特殊的线性组合系数，但它的增补方程仍然是特征向量所满足特征方程的求导式，那么可以说在这两种技术线路下的直接法都不可避免地需要考虑特征向量的规范化条件作为技术适用性的背景。

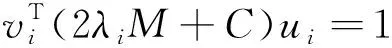
2 涉及重频问题的相关算法

Dailey[15]和Curran[16]的算法是针对重特征值的导数不同的情况，Shaw[18]和Friswell[19]推广了Dailey和Curran的算法至重特征值的导数也是相同的情况，Shaw的算法可以求重特征向量的二阶导数，而Friswell的算法只能求其一阶导数。

吴柏生等[20]在求特解V时，推广了Nelson的方法，该方法也假定重特征值的导数全不相同，使得调整后的支配方程的系数矩阵的条件数相对较小。文献[21]～[22]在求特解V和vi时所使用的技术与Ojalvo处理单频问题时的方法相类似，不像Nelson方法那样置换一些元素，而是通过在支配方程组中增补规范化方程来实现求解特解。吴柏生等[23]考虑某个重特征向量的导数问题时，还提出了求解特解vi的迭代算法，更适合大规模有限元分析。张德文等[24-28]提出了动柔度法、高精度动柔度法，实用动柔度法及混合移频动柔度法等。动柔度法或称逆直接法，避免了转换m个约束到特征导数支配方程中，代之以广义逆技术或直接扰动技术求解单或重特征问题在直接法框架下的特解。Tang和王文亮[29]提出了直接法和模态法的联合方法，求解重特征向量的二阶导数，章永强等[30-32]讨论了重特征向量导数的存在性，以及在以灵敏度矩阵方程型模型修正框架下，用广义逆技术等计算灵敏度矩阵的逆，称之为逆灵敏度方法。除了文献[21]和[29]是针对非对称广义重特征问题以外，其余都是对称广义重特征问题(无阻尼对称系统)的特征导数的计算方法。

3 结语

综上所述，模态灵敏度的直接法，近年来有了较大发展，但它仍存在如下问题尚需解决：

1)在Nelson提出的直接法主要框架中，在求特解vi时，关于支配方程的系数矩阵的调整策略，只是给出相对合理的解释，在理论上并非强有力的支撑。它们更偏重算法介绍，而数值结果的精度分析和比较有所缺失，而近年来的直接法文献在求特解V或vi时则偏重于迭代技术、扰动技术和广义逆技术等数值方法的融合，因此，类似的直接法在使用时就必须考虑精度和收敛性，而对一般的使用者而言这种问题的讨论存在一定的难度。

2)对单特征问题，直接法框架下的ci的确定依赖于所要求导的那阶模态所满足的某种规范化条件，对重特征问题，算法中的C或ci的确定也依赖于重特征向量所满足的不同的规范化条件，这既是一种约束，也是未来算法发展的潜在空间。