大型单摆式游乐机械设备动力学建模研究
2019-03-16陈金舰吴婷婷
陈金舰,吴婷婷
(湛江幼儿师范专科学校 岭南师范学院基础教育学院信息科学系,广东 湛江 524000)
0 引言
大型单摆式游乐机械设备广泛应用在大型游乐场中,单摆式游乐机械设备的转动力学控制是保障设备安全稳定运行的关键。对单摆式游乐机械设备的优化力学控制模型进行研究,采用自适应力学建模方法进行单摆式游乐机械设备的优化参数调节,建立单摆式游乐机械设备的动力学模型,可以提高单摆式游乐机械设备的稳定性控制能力。[1]对单摆式游乐机械设备的建模是建立在力学参数采样基础上的,结合机械部件的耦合控制,进行单摆式游乐机械设备的力学参数分析,提高单摆式游乐机械设备的力学输出稳定性。在传统方法中,大型单摆式游乐机械设备的动力学建模主要采用是模糊PID建模方法[2]进行大型单摆式游乐机械设备运行的控制律设计,但该方法的控制稳定性不高,多轴调节和力学稳定性控制的效果不好。针对上述问题,提出基于非线性多刚体动力学分析的大型单摆式游乐机械设备的动力学建模方法,构建大型单摆式游乐机械设备的转向动力学模型以及动力学参量自适应调节模型,采用模糊自适应律进行大型单摆式游乐机械设备的自适应控制,和非线性多刚体动力学分析模型,实现大型单摆式游乐机械设备动力学建模。最后进行仿真测试,得出有效性结论。
1 大型单摆式游乐机械设备的动力学模型及参量调节
1.1 大型单摆式游乐机械设备的动力学模型
为了实现大型单摆式游乐机械设备的动力学建模,以输出转向力矩和负载力矩等为约束参量,进行机械设备的机械式变刚度柔性调节,采用陀螺仪、加速度计为敏感元件进行大型单摆式游乐机械设备的参数采集[3],大型单摆式游乐机械设备核心结构如图1所示。
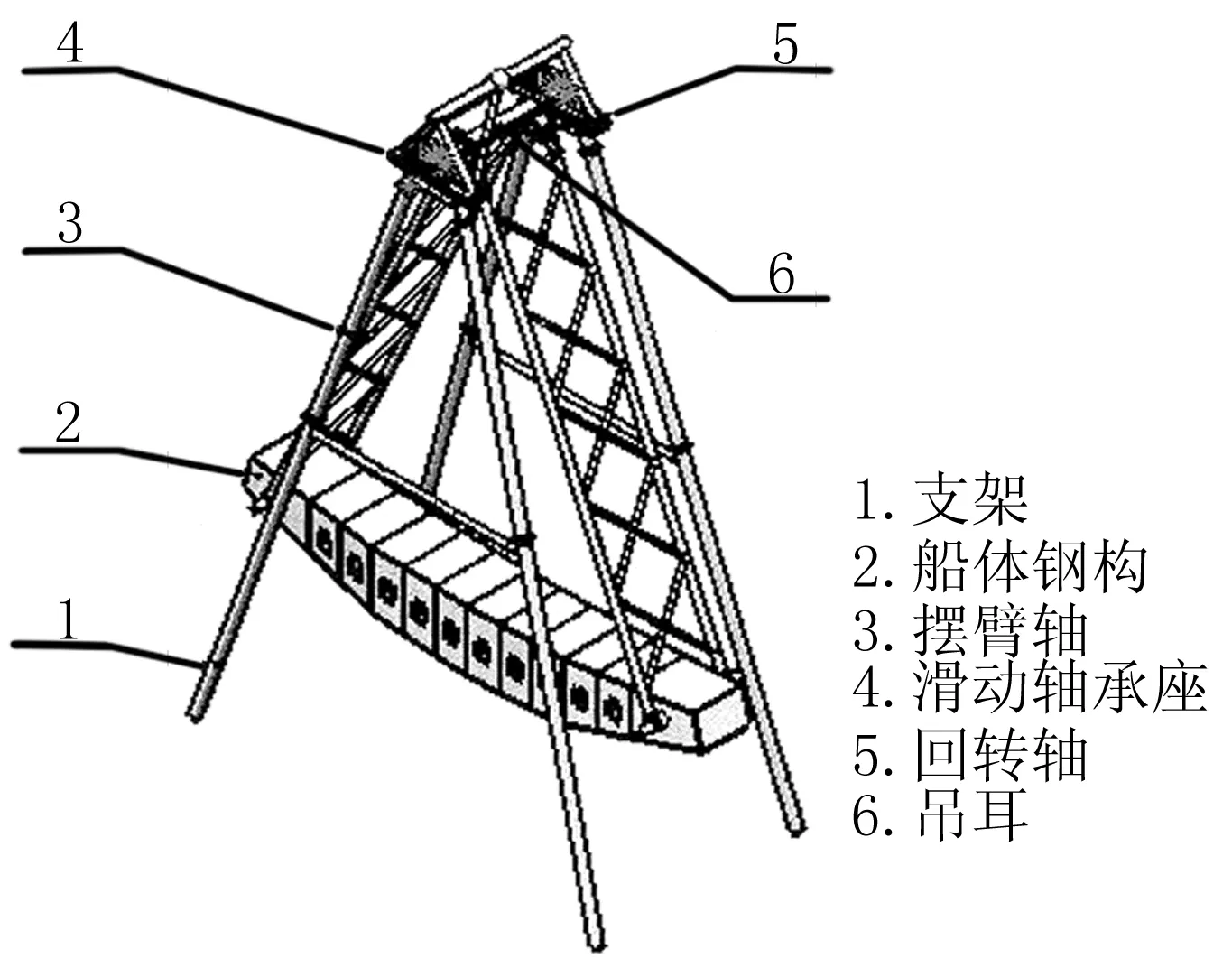
图1 大型单摆式游乐机械设备核心结构
采用拉力和刚度稳态调节方法,进行大型单摆式游乐机械设备动力学参数融合处理,实现多自由度并联柔性参数的自适应融合,结合Kalman滤波融合方法[4],进行大型单摆式游乐机械设备的多轴转向参数调节,在不确定性干扰作用下,构建大型单摆式游乐机械设备在各个方向的运行动力学方程(图2~3)。
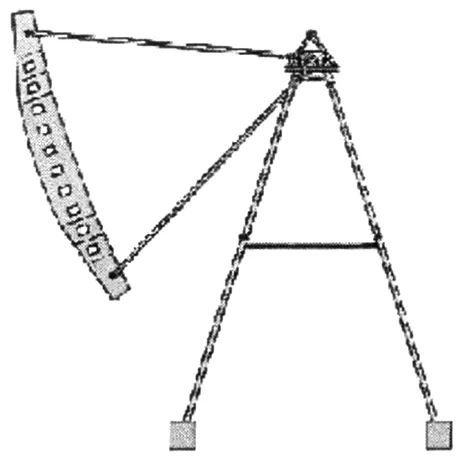
图2 大型单摆式游乐机械设备纵向运动

图3 大型单摆式游乐机械设备侧向运动
纵向运行动力学方程为
(1)
侧向运行动力学方程为
(2)
式中:m为大型单摆式游乐机械设备的质量;V为大型单摆式游乐机械设备的转向速度矢量(Ox2轴)与水平面间的转矩;Fy为整个单摆旋转过程中的输入惯性矩;Jz为单摆式游乐机械设备的绳索驱动转矩;Mz1为多自由并联柔性驱动力矩;θ为变刚度装置结构的倾角;α为侧向力。
对大型单摆式游乐机械设备的输入惯性力矩进行扰动调节,采用分段力学控制方法[5],得到大型单摆式游乐机械设备的运动学模型描述为式(3)的非线性方程组:
(3)
式中:P为转向力矩;SM为动、定滑轮间绳索长度;lR为大型单摆式游乐机械设备对体坐标系Oz1的惯性积;q为后阶段永磁体间磁力。
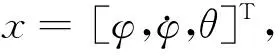
1.2 力学参数调节
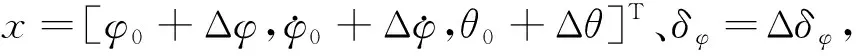

(4)
式中:α为驱动电动机的输出动力;Fgr表示单摆式游乐机械设备电机的电枢电流;JR表示电枢电感;Mgr表示操作臂的刚度阻尼系数,考虑不同位置与刚度的耦合特性,构建状态量约束方程,得到大型单摆式游乐机械设备的动力输出控制约束参量分布模型为:
(5)

根据上述分析,构建大型单摆式游乐机械设备的转向动力学模型,以输出转向力矩和动力负载为约束参量,实现力学参数调节[7]。
2 机械设备动力学建模的优化设计
2.1 大型单摆式游乐机械设备的自适应控制
在上述构建大型单摆式游乐机械设备的转向力学参数调节模型的基础上,进行机械设备动力学建模的优化设计,提出基于非线性多刚体动力学分析的大型单摆式游乐机械设备的动力学建模方法,大型单摆式游乐机械设备模态参数识别输出:
(6)
式中μMCMA代表轴向位置度,结合各精度指标的误差数据进行变刚度装置自适应参量修正,得到大型单摆式游乐机械设备在转动过程中的优化参数调节输出为:
(7)
操作臂重力与绳索拉力存在一个静力平衡关系,以大型单摆式游乐机械设备比例调节参量为输入,构建反馈跟踪调节模型,操作臂上引入转动量,得到自适应调节函数为:
(8)
在线性观测模型下,刚度与位姿解耦控制的反馈增益为:
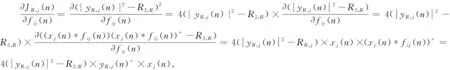
(9)
采用非线性多刚体动力学分析模型,实现大型单摆式游乐机械设备动力学建模及惯性调节方法,构建大型单摆式游乐机械设备的控制律,实现位置与刚度的耦合调节[8]。
2.2 大型单摆式游乐机械设备动力学建模
采用模糊自适应律进行大型单摆式游乐机械设备的自适应控制,采用非线性多刚体动力学分析模型及多模控制方法,得到大型单摆式游乐机械设备动力学误差函数为:
eR,j=(|yR,j(n)|2-R2,R)×yR,j(n)*。
(10)
构建大型单摆式游乐机械设备动力学建模的迭代方程为
fij(n+1)=fij(n)+μMCMA×((|yR,j(n)|2-R2,R)yR,j(n)*+j(|yI,j(n)|2-R2,I)yI,j(n)*)×xj(n)。
(11)
采用模糊自适应律进行大型单摆式游乐机械设备的自适应控制,得到观测器观测误差函数为
(12)
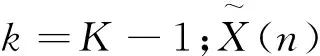
(13)
式中B=[b1(θ1),b2(θ2),...,bq(θq)]T,根据大型单摆式游乐机械设备的压力波动变化,得到输出状态参量为θi和扩展角σi,综上分析,得到大型单摆式游乐机械设备的动力学参量调节矩阵R定义为
R=X(n)XT(n)=
(14)
动力学反馈状态方程为
(15)
其中:
(16)
(17)
(18)
(19)
综上设计,实现了大型单摆式游乐机械设备的动力学建模。
3 仿真实验与性能分析
为了验证本文方法在实现大型单摆式游乐机械设备在动力学建模和优化控制方面的应用性能,进行仿真试验分析,单摆式游乐机械设备的电动势系数为0.056 V·s/rad,传动效率为0.34,机械设备等效阻尼系数为0.012 N·ms/rad,杆件转动惯量为2.35,自适应调节系数b1=0.1,b2=-14.6,b3=14,根据上述仿真环境和参数设定,进行单摆式游乐机械设备的动力学建模分析,得到单摆式游乐机械设备的力学参数仿真分析结果如图4所示。
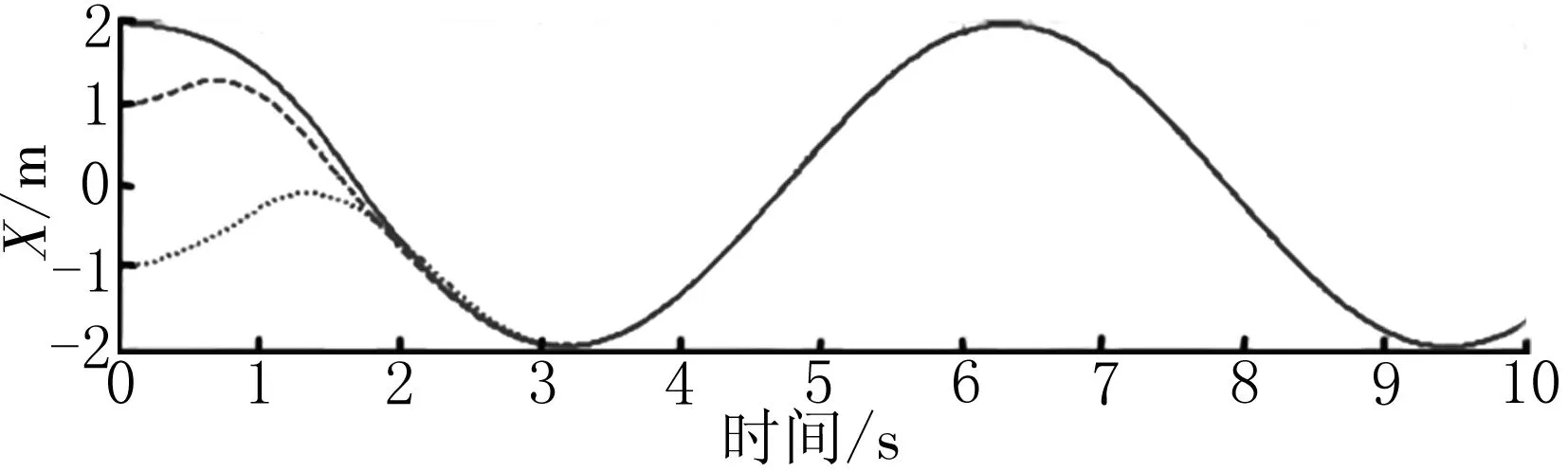
图4 单摆式游乐机械设备的力学参数仿真分析结果
以图4的单摆式游乐机械设备的力学参数分布为研究对象,进行大型单摆式游乐机械设备的优化控制,得到控制输出如图3所示。
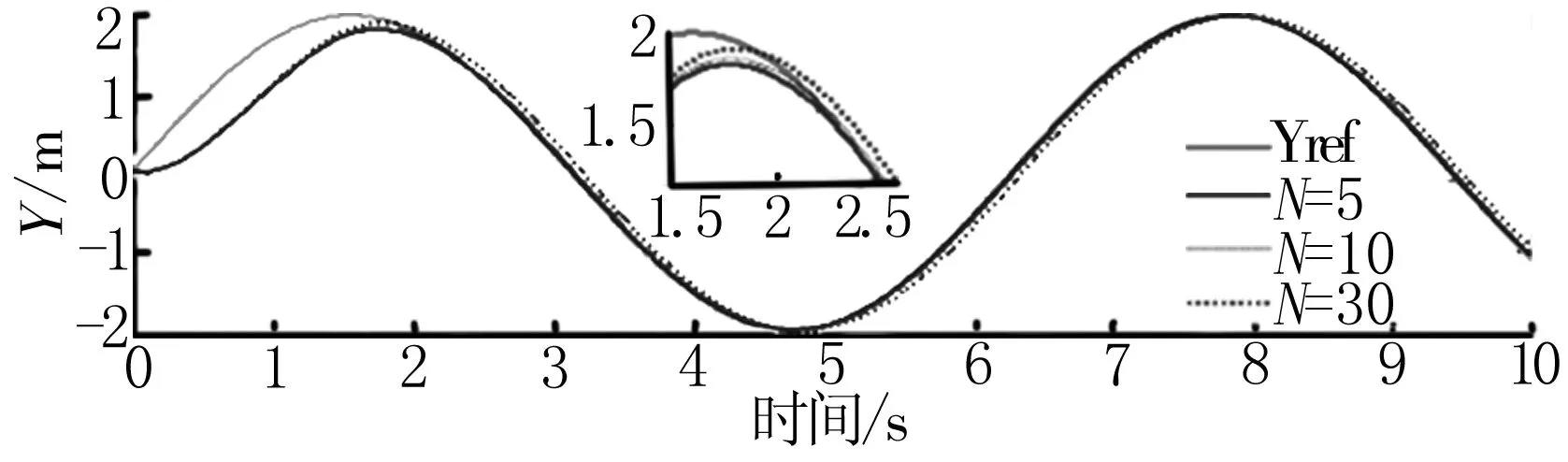
图5 控制输出
分析图5得知,采用本文方法进行大型单摆式游乐机械设备控制的输出自适应性较好,力学建模的稳定性较好。为了验证本文方法的有效性,对本文建模方法、模糊PID建模方法和积分建模方法的控制误差进行对比分析,得到对比结果见表1。
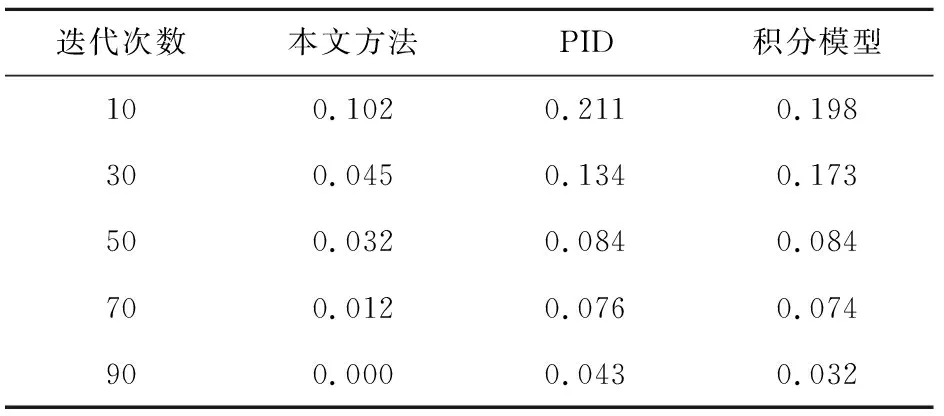
表1 误差分析
分析表1得知,随着迭代次数的增长,3种方法进行大型单摆式游乐机械设备的动力学建模的误差逐渐减少,本文方法的大型单摆式游乐机械设备的动力学建模误差最低为0,比模糊PID建模方法和积分建模方法的控制误差小,说明本文方法进行大型单摆式游乐机械设备的动力学建模的误差小,收敛性较好。
为了进一步验证本文方法的有效性,对本文建模方法、模糊PID建模方法和积分建模方法的模型计算时间进行对比分析,对比结果如图6所示。
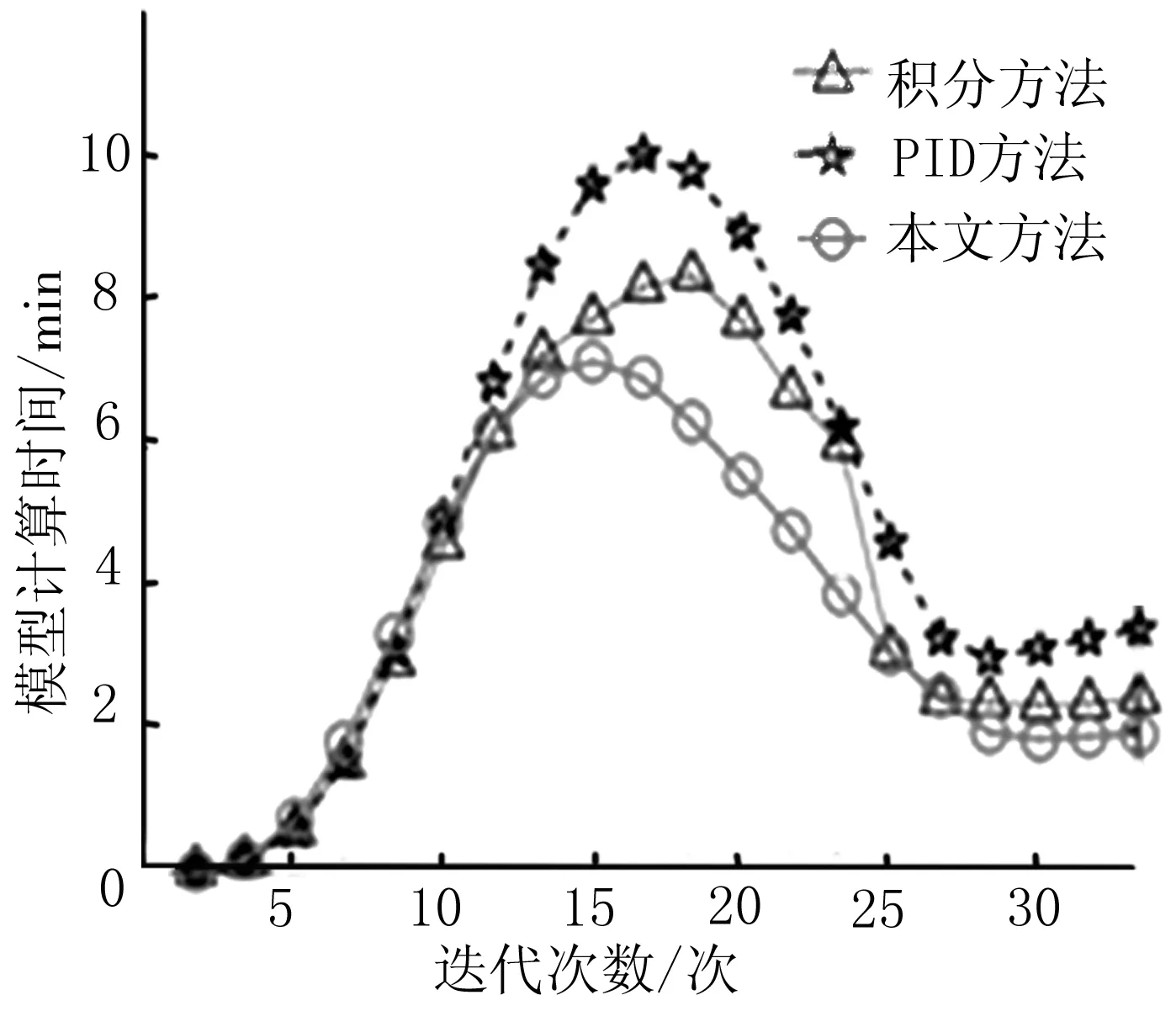
图6 3种方法的模型求解时间对比
根据图6可知,本文建模方法的单摆式游乐机械设备的动力学模型计算时间最高为7 min,比模糊PID建模方法和积分建模方法的模型计算时间短,说明本文方法的建模时间较快。
4 结语
采用自适应力学建模方法,进行单摆式游乐机械设备的优化参数调节,建立单摆式游乐机械设备的动力学模型,从而可以提高单摆式游乐机械设备的稳定性控制能力。本文提出了基于非线性多刚体动力学分析的大型单摆式游乐机械设备的动力学建模方法,构建大型单摆式游乐机械设备的转向动力学模型,进行了大型单摆式游乐机械设备动力学控制模型设计,构建大型单摆式游乐机械设备的动力学参量自适应调节模型,采用模糊自适应律进行大型单摆式游乐机械设备的自适应控制,采用非线性多刚体动力学分析模型,实现了大型单摆式游乐机械设备动力学建模。分析得知,运用改进的方法进行大型单摆式游乐机械设备动力学建模的输出其稳定性较好,误差较小,具有很好的力学建模能力。
