大坝下游河床潜流带温度场的影响因素研究
2019-03-15刘豪杰
任 杰,刘豪杰
(西安理工大学 水利水电学院, 陕西 西安 710048)
河流中大坝建成后,坝前后的河流水位及流速发生改变,坝前水位抬升引起水温呈现垂直分层现象,分层水温通常为上层水温高,下层水温低[1]。水库下泄水温与天然河流水温存在显著差异,对河床潜流带内水热交换有一定影响。水温也是影响河流及其邻近地区(如河岸带、洪泛区和潜流带)的水生生态系统重要的因素之一[2]。因此,越来越多的研究学者认识到地表水-地下水相互作用的重要性。陈孝兵等[3]构建了循环式水槽装置,基于扩散模型,研究了不同河床地形的潜流交换与地表水动力及河床渗透特性之间的关系。刘东升等[4]以新安江大坝下游为研究对象,对比分析了该水库下游河岸带冬夏季潜流交换特征及温度场分布规律。陈斌等[5]揭示了渗流仪的不同装置结构对潜流交换的影响。李英玉等[6]研究了新安江大坝下游河岸带温度场时空分布特征,并基于一维瞬态解析模型对地下水流速进行了求解。国外专家,Norman等[2]构建了循环式水槽装置,研究了3种河床地形、3种水流流量和2种渗透特性情况下河床潜流带热流传输规律。Mamer等[7]通过构建一个循环式水槽装置,并利用一维瞬态解析模型对地下水和地表水的相互作用进行了量化,结果表明一维瞬态解析模型方法在精细尺度上能够准确定位和量化潜流交换通量。Sawyer等[8]使用了实验室水槽试验和数值模拟两种方法对潜流和热交换进行了量化。上述大都是针对单一因素影响下河床潜流带的规律研究,并未针对多种因素共同影响下河床潜流带的温度场影响规律变化问题进行研究分析。
本文构建一个概化水槽模型,并以水温作为一种示踪剂,基于雷诺平均方程(RANS)和k-ω湍流模型,利用商业有限元软件CFD-Fluent和COMSOL Multiphysics进行求解,并对模型参数进行Morris全局灵敏度分析,研究大坝下游河床潜流带内温度场在水流流速、河道水位、沙坡高度和河床渗透系数等单因素和多因素影响下的变化规律。
1 数学模型
1.1 流体控制方程
Patel等[9]和Yoon等[10]通过二维水槽试验与数值模拟对比了相同边界条件下沙波上方流速分布、漩涡大小、阻力系数等特征因素,结果显示k-ω湍流模型对刻画沙波上方紊流结构具有较好的适用性。
对于不可压缩流体,雷诺平均方程为[11-12]:

(1)
(2)
(3)

雷诺应力与湍流动能k比率耗散系数ω有关,其计算式为:
(4)
vt=k/ω
(5)
式中:式中δij为克罗里克符号。
湍流动能k方程为:
(6)
耗散系数ω方程为:
(7)
1.2 多孔介质渗流控制方程
河床饱和多孔介质中渗流连续控制方程为[13]:

(8)
式中:ρf为水体密度,kg/m3;v为渗流速度矢量,m/s。
1.3 多孔介质温度场控制方程
河床多孔介质中的温度传播采用对流传热方程,其计算式为[14]:
(9)
式中:εp为多孔介质孔隙率;cw为水体导热系数,J/(kg·℃);ρs为多孔介质密度,kg/m3;cs为多孔介质导热系数,J/(kg·℃);Tw为水温,℃;λij为多孔介质导热系数,W/(m·℃);QT为热(汇)源项。
2 计算模型
参考Norman等[2]的室内水槽物理模型,河床为5.0 m(长)×0.7 m(高),床面有9个沙坡,沙坡有效范围为0~4.5 m。单个沙坡0.5 m(长)×0.05 m(高)。地表水水位为0.1 m。地表水-地下水数值模型的概念模型如图1所示。以2.0 m~3.5 m之间的区域作为研究对象,研究区域内河床监测点布设5行×7列,如图2所示。地表水模型采用CFD-FLUENT建模并求解,共划分1 058 125个网格单元;地下水模型采用COMSOL Multiphysics建模并求解,共划分97 158个网格单元。


2.1 边界条件
水力边界:河流水位ac边为定水头边界,bd边为自由出流,ab为对称边界,cd边界为不可移动的墙边界;cd边界为压力边界,ce、ef、df边界均为不透水边界。
温度边界:多孔介质模型中,ce、ef、df边界均为绝热边界,cd边界温度与水体温度相同。
初始条件:初始流速为0.14 m/s,水深为0.1 m。水流水温为10℃,河床底质渗透系数k和初始温度分为0.033 m/s和20℃。
2.2 模型参数
模型所需的水力及热力学特性参数从文献[2,14-15]中进行选取,模型参数见表1。

表1 模型参数
2.3 全局灵敏度分析
考虑到所建立的模型参数灵敏度对输出结果的影响,本文选取Morris方法[15]对河床潜流带温度场的影响因素进行全局灵敏度分析,具体计算步骤参考文献[15]。本文选取坡高h,流速v,沉积物渗透系数k和水深H等4个因素,进行灵敏度分析。数值计算时,各因素按照20%增加进行求解,模拟时间为24 h。
3 结果分析
3.1 全局灵敏度分析
根据各因素排列方式得到10种因素组合,并进行数值求解,结果如表2所示。由表2可知:
(1) 针对单一因素分析,流速v和水深H是影响河床潜流带温度场的主要因素,但从流速v和水深H对河床温度场作用的幅度来看,流速v对河床潜流带温度场的影响是负相关的,而水深H对河床温度场的影响是正相关的。
(2) 针对多因素分析,组别7、8、10河床潜流带温度场的影响较大,均呈现负相关。组别9影响最小。
(3) 考虑这10组因素组合,单个因素变化或因素组合变化均会影响河床潜流带的温度场。
3.2 温度场分析
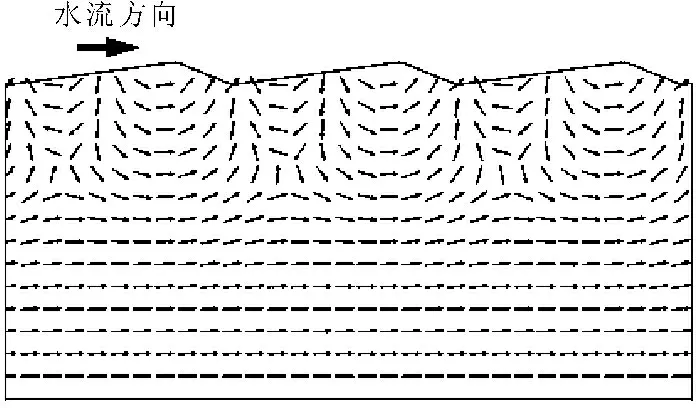
由图3可知,研究区域内的温度场等值线在模拟结束时均会在沙坡下面会出现一个半圆型的低温区域。结合图4和图5可知,迎水面压力大于背水面,导致地下水从压力大处向压力小处运动,使沙坡下出现一个半圆的低温区域。由图3(a)、图3(b)可知,当流速v增大时,研究区域内温度场等值线均有所向下降的趋势。图3(c)是流速v、水深H、河床底质渗透系数k和沙坡高度h等4个因素均发生变化情况下的河床研究区域内的温度场变化情况,相比额定温度场(见图3(a))和流速v发生变化(见图3(b))情况而言,多因素共同变化对河床影响的更为明显,说明考虑多因素共同影响更能反映河床真实状态下的温度场变化规律。

表2 全局灵敏度分析因素组合及温度变幅
4 结 论
本文基于雷诺平均方程(N-S方程)、k-ω湍流模型,并利用CFD-Fluent及COMSOL Multiphysics软件,构建地下水-地表水耦合模型;通过Morris全局灵敏度分析方法探讨单因素影响及多因素影响下河床潜流带内温度场变化规律,结论如下:流速v、水深H、河床底质渗透系数k和沙坡高度h等。


(1) 针对单一因素,河床潜流带温度场受水流流速v、河道水位H的影响最为明显,其次为沙坡高度h和河床渗透系数k;针对组合因素,坡高h和渗透系数k组合、流速v、水位H和坡高h组合以及流速v、水位H、坡高h和渗透系数k组合等3个组合对河床潜流带温度场影响较大。
(2) 河床潜流带的温度场受河床表面压力分布影响,且在沙坡下会出现一个半圆的低温区域;在多因素共同影响下,河床潜流带温度变化较为明显。
