发育软弱结构面土坡破坏细观机理研究

2019-03-15郑泽松熊传祥

水利与建筑工程学报 2019年1期

郑泽松，熊传祥，王涛

(1.福州大学环境与资源学院，福建福州 350116； 2.中化地质矿山总局福建地质勘查院，福建福州 350013)

边坡稳定性一直是岩土界关心的问题，由于环境地质条件的差异，导致其破坏过程和影响因素复杂多变，坡体的变形、失稳从本质上是坡体为了自身达到平衡状态的自我调整过程。目前对节理软弱面的研究多集中在岩质边坡，如李馨馨等[1]、潘皓等[2]、Jiang等[3]、杜光勤等[4]、Su等[5]、曾海艳等[6]对多节理岩质边坡稳定性进行了模拟分析。但对土坡中裂隙软弱面研究的较少，因此本文选取福建安溪县深厚的花岗岩残积土为研究对象，分析发育多组软弱面土坡的破坏机理。

离散单元法是一种模拟非连续介质大变形的数值模拟方法，目前广泛应用于岩石力学、土力学等领域的数值模拟。目前，ITASCA公司的颗粒流模拟软件PFC3D是基于离散元理论的优秀商业软件之一，其原理是将非连续介质集合体离散成独立的颗粒单元，反复运用牛顿第二定律更新各颗粒的运动状态，并结合力-位移定律，建立每个颗粒的运动方程，通过循环运算，采用显式中心差分法求解方程[7]。该方法只需定义颗粒的接触关系即可，跳过了给土体定义本构模型的复杂步骤，便于模型的建立。利用离散元理论，苗晨曦等[8]、任刚等[9]、李晓锋等[10]、黄玉祥等[11]、史旦达等[12]、朱德福等[13]分别研究了土工格栅材料的复合性能、结构面岩质高边坡失稳预测、类节理岩石直剪试验力学特性、深松土壤扰动行为、饱和砂土自由场地地震液化特性以及破碎岩体压实特性，结果均与试验较为符合，验证了其在数值分析方面所具有的优越性。由于土是特定的自然地质环境中形成的松散堆积物，基于离散元理论的PFC3D通过考虑土体材料本身的不连续性，从细观角度对土坡破坏的整个过程进行模拟。

1 研究区软弱面描述

安溪县地层以中生界侏罗系火山岩分布最广，其中以燕山期形成的各类花岗岩为主，出露面积约998 km2，约占全县总面积的1/3[14]。这为发育疏松、深厚的基岩风化壳提供了良好的物质基础，由于花岗岩原岩中存在大量原生和构造结构面，这些结构面相互切割穿透，随着花岗岩风化成土，花岗岩残积土内部也残存了部分花岗岩的结构和构造特征，使花岗岩风化壳中存在大量的软弱结构面，并且在风化过程中还将产生次生节理和卸荷裂隙等软弱面。由于这些结构面的存在，使花岗岩残积土风化剧烈，且往往是地下水富集区，导致岩土力学性质变差[15]，相应地，坡体的破坏往往会追踪这些软弱面。若忽略这些结构面影响是不切合实际的，因此，本文根据花岗岩残积土中结构面特点，分析花岗岩残积土中存在软弱结构面时边坡的破坏机理。

某公路段穿过深厚的花岗岩残积土层，地层以残积砂土层为主，底部为碎块状强风化。经现场调查发现，软弱面产状主要存在4个明显的优势面，即238°∠79°、115°∠74°、323°∠23°、338°∠47°的优势面。随着人工开挖边坡，其内部发育的软弱结构面暴露于地表，不良地质结构面组合对边坡稳定性有直接影响，尤其是顺倾的软弱面，因此本文将对此开挖边坡进行仿真模拟，研究软弱结构面对土坡破坏机理造成的影响。

2 建立计算模型

2.1 边坡模型尺寸的选取

本文参照福建省安溪县某一典型开挖边坡，为简化数值模拟工作，本文模型材料选用单一的花岗岩残积砂土层作为研究对象，模型概化后，取单位宽度进行分析。模拟区域长15 m，高13 m，其中坡高为10 m，坡顶宽度为8 m，坡底宽度为11 m，坡率为1∶0.33，具体尺寸如图1所示。

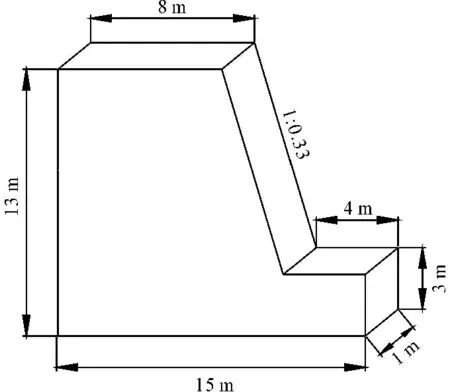
2.2 细观参数的选取

PFC3D模拟要求数值模型的力学特性与实际材料相符，而对于颗粒大小并不要求与实际一致，且若颗粒大小取用与实际土颗粒大小一致，计算量将极其浩大，由于本论文主要是讨论多组裂隙发育情况下边坡的破坏机理，而非具体量值，因此模拟所用颗粒大小取自数值三轴试验，其物理力学性质与地基土相符合。通过建立PFC3D数值三轴试验模型，并与室内三轴试验应力应变曲线拟合，最终获得花岗岩残积土的细观参数，具体见表1。

表1 残积砂土的细观参数

2.3 软弱面的生成及属性设置

在PFC3D中，通过JSET命令来设置岩土体内部的软弱结构面，能够很好地模拟颗粒组间的滑移和分离[16]。但只有在颗粒间存在法向接触力的情况下，才能够设置节理面接触，因此，节理面需在模型颗粒生成并达到平衡后才能执行。JSET命令可以单独生成一条或者一组软弱结构面，通过配合Dip和Origin关键词，能够在指定位置生成软弱结构面，其中Dip是指结构面的倾角，Origin是指软弱面所经过的某一点的坐标。最后，采用PROPERTY命令赋予节理面属性。根据崩岗坡体内部软弱结构面的胶结和充填情况，将其细观参数设置为坡体颗粒连接强度的二分之一，软弱结构面的细观参数见表2。

表2 软弱结构面细观参数

2.4 建立边坡模型

本文PFC3D建立的坡体模型由两个长方体和一个三棱柱组成，且各自在x、y、z方向的尺寸分别为1 m×15 m×3 m，1 m×8 m×10 m和1 m×3 m×10 m。

模型由8道墙面限制外边界，其中在3个区域内不重叠、随机生成的颗粒粒径范围在0.12 m～0.16 m,生成颗粒总数为7 047，模型孔隙率为0.40。生成颗粒时，先生成1/2粒径的颗粒，然后再将粒径扩大2倍，以使前后生成的颗粒不发生重叠。模型采用接触粘结，首先进行先期土体自重平衡计算，运行计算9 000时步，使颗粒平均不平衡力与平均接触力的之比小于0.1%，即可认为坡体模型达到初始稳定[17]，方能进行后续计算。由于顺倾软弱面对坡体的稳定性影响更大，选取两组顺倾结构面进行分析。此时通过JSET命令对模型进行软弱结构面设置，两组结构面倾角分别为20°、45°，间距均取1.5 m，具体模型见图2。

3 模拟结果分析

3.1 坡体破坏形态分析

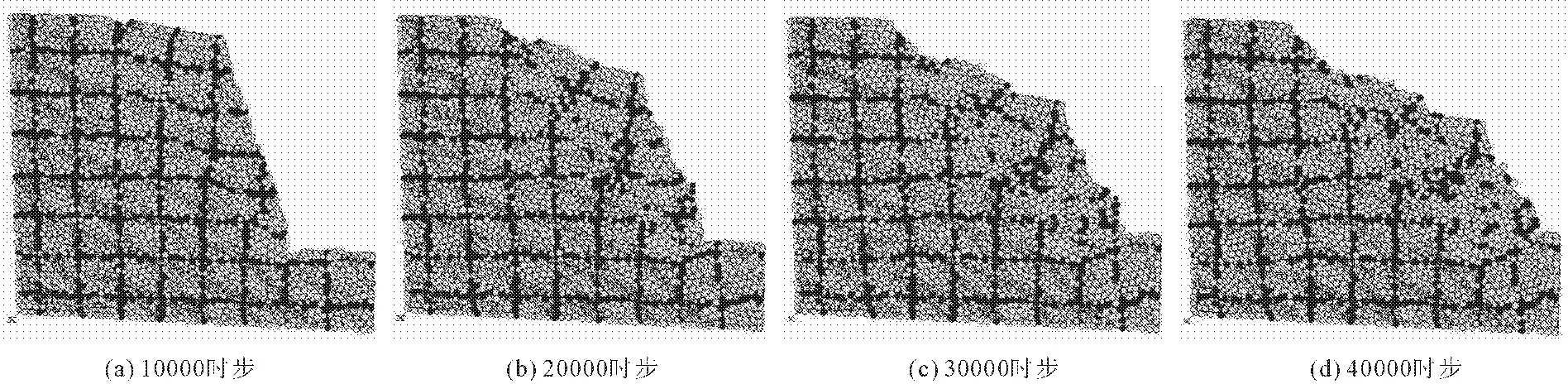
用深色网格将模型划分成不同区域，以便于坡体破坏形态观测(见图3)。模型计算到10 000时步时，坡顶在y=4 m处附近沿着节理面出现一条张裂缝，坡体在坡脚处附近沿节理面出现微小的隆起，坡体内部颗粒沿着软弱面有微小错动，坡肩有少量的沉降变形(见图3(a))。计算到20 000时步时，坡体沿着最危险滑动面发生滑移，滑塌体表明有少量颗粒发生剥落，坡底受到挤压，产生向上的隆起现象(见图3(b))。计算到30 000时步时，坡体变形量增大，滑动面后缘与软弱面重合，坡底颗粒向上隆起量增大(见图3(c))。计算到40 000时步时，滑塌体内部结构较为破碎，堆积于坡底(见图3(d))。

3.2 坡体应力分析

通常情况下，在分析连续体介质力学性质时，计算的是应力和应变，但在离散介质中却难以计算应变。离散介质是由一定数量的颗粒组成，其中各个颗粒会发生平动和转动，从而极大地影响到整个颗粒集合体的力学性质，因而可对此颗粒集合体给出一个平均的应变[18]的概念，即将岩土体视为由众多颗粒集合体所组成的材料，并在代表性部位设置测量区，取测量平均值作为岩土体的应力和应变。PFC3D在模型中可以设置测量圈，每个测量圈内包含一定数量的颗粒，可以记录不同情况下以及不同运算时步下测量圈内的孔隙率、应力和应变等变化规律。

为了获得初始强度条件下崩岗坡体的应力等值线图，可以在边坡内部设置足够多的测量圈(见图4)，利用自编FISH程序，把测量圈的应力数据导出，通过Surfer绘图软件能将边坡的应力等值线画出。

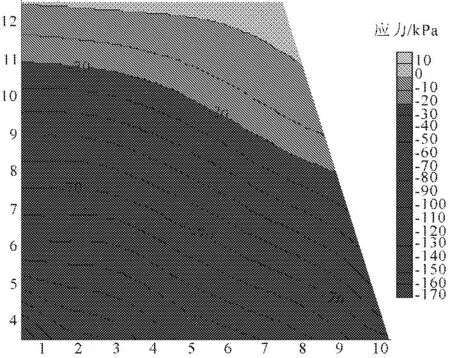
由于边坡发生较大的变形破坏，颗粒沿最危险面朝坡底移动，坡体内部应力重新分布，两个方向的应力都沿临空面方向有偏移。在原坡肩部位附近颗粒发生滑移，此处测量圈内部没有颗粒存在，实际上应力数值为0 kPa，但由于边坡应力是通过Surfer软件自动填充完成，因此与实际情况略有差异，但此附近颗粒应力等值线特别疏松。y方向最大压应力在坡底中部位置，数值为65 kPa(见图5)。z方向最大压应力在坡体左下角，数值为170 kPa(见图6)。结果基本符合实际边坡中水平与竖向应力的关系，即水平应力等于竖向应力乘以侧压力系数。

3.3 边坡位移分析

坡体位移等值线如图7、图8所示，y方向颗粒最大位移在滑塌体最前沿位置，数值范围在3.85 m～4.62 m之间，位移等值线并不光滑，呈锯齿状，滑动面总体呈圆弧面。z方向颗粒最大位移在滑塌体中上部位置，即原坡肩附近，数值范围在4.25 m～5.10 m之间，z方向位移等值线呈块状，具有明显的锯齿形，且比y方向位移等值线更明显。从图中可以推断出，坡体内大量软弱面对坡体的滑移变形有较大影响。

3.4 速度矢量分析

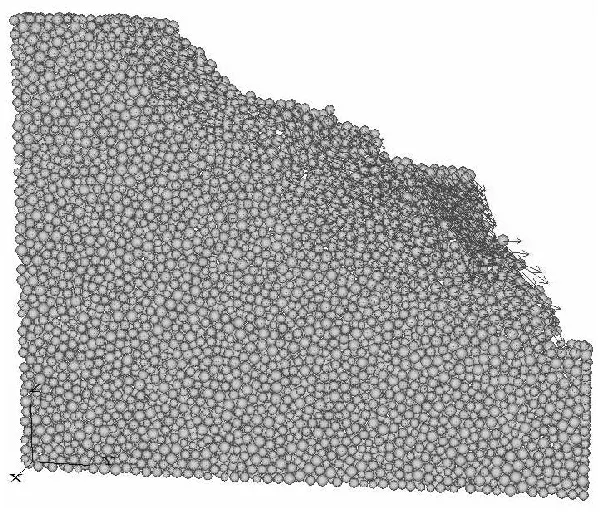
从坡体的颗粒的速度矢量图可以看出(见图9)，颗粒的最大速度为0.641 9 m/s2，速度矢量在原坡肩位置附近最大，愈往坡体内部速度愈小。滑塌体主要速度矢量方向超坡底往下，当在滑动面附近速度矢量方向较杂乱，各个方向都有，这是由于滑动面附近颗粒由于颗粒发生滚动的原因。

图7 y方向位移等值线图

3.5 微裂缝发展情况分析

由于边坡计算为接触粘结模型，通过FISH语言编程，可以记录颗粒间的接触开裂情况，只要接触被破坏就判定为发生一个微裂缝，边坡内部微裂缝发展情况下：开始时，坡体内部微裂缝增加速率较快，曲线较为陡峭；随着边坡开始发生滑移，微裂缝发生增加速率逐渐趋于平缓。坡体内部一共有32 987个接触粘结，当模型运行40 000时步时，微裂缝发展数量为6 847个，可以看出坡体发生滑移后，粘结破坏数量占总数的20.76%。

通过统计微裂缝发展个数、观察微裂缝的发展变化，可以推测出，当微裂缝数量足够多时，在重力作用下，容易在边坡中逐渐形成连续贯通面，导致坡体发生滑移破坏。