均布荷载作用下变截面波形钢腹板组合箱梁剪应力的分布与计算

2019-03-15冀伟，魏源，罗奎

水利与建筑工程学报 2019年1期

冀伟，魏源，罗奎

(兰州交通大学土木工程学院，甘肃兰州 730070)

波形钢腹板组合箱梁是用波形钢腹板取代了传统混凝土箱梁腹板的一种钢-混组合结构，它充分利用了钢材的抗拉性能与混凝土的抗压性能，以充分发挥材料各自的优点[1]，显著改善该组合结构的力学性能并且提高了经济型，大大降低了桥梁上部结构的自重[2]，使得桥梁的跨越能力达到了一个新的水平，这种结构的桥梁具有许多优点，包括避免了传统混凝土腹板宜开裂的弊端、提高了预应力效率、力学性能突出、结构简单、外形美观、施工方便、经济效益显著[3-9]等，由于波形钢腹板的褶皱效应，其腹板几乎不抵抗轴向力[10]。自从波形钢腹板PC组合箱梁出现，许多国家修建了这种类型的桥梁，1986年法国建成了世界上第一座组合箱梁桥——Cognac高架桥，日本于1993年修建了日本首座波形钢腹板PC简支箱梁桥——新开桥，近年来，随着制造工艺、施工技术和波形钢腹板PC组合箱梁设计理论的逐渐成熟，波形钢腹板箱梁桥在现代大跨度桥梁中具有显著的竞争力，考虑到经济和技术的合理性，梁一般采用变截面梁。

现有文献中，国内外许多学者对波形钢腹板钢-混组合梁桥的剪应力等性能进行了研究：Hassanein等[11]研究了波形钢腹板的临界剪切屈曲应力。Wang S等[12]研究了波形钢腹板组合梁的抗剪强度、剪切刚度和破坏模式。Qiao P等[13]基于手风琴效应研究了不同尺寸参数对扭转变形应力的影响。乔朋等[14]研究了单箱多室波形钢腹板组合箱梁的腹板剪应力，提出单箱多室波形钢腹板组合箱梁的钢腹板剪应力计算应包括弯曲剪应力、扭转剪应力以及局部畸变产生的剪应力。李杰等[15]考虑变截面效应，研究了变截面波形钢腹板组合箱梁腹板剪应力的实用计算方法，提出了变截面梁的梁高和底板厚度的变化对剪应力有较大影响。邓文琴等[16]以某单箱五室波形钢腹板组合梁斜拉桥为研究对象，分析了施工阶段应力叠加作用下各腹板的剪应力分布和剪力分配比例。武海鹏等[17]考虑梁高、底板厚度的变化，推导了钢腹板剪应力计算公式及剪力传递效率，得出变截面波形钢腹板梁中的剪应力除了由截面剪力Q引起外，还包括有截面弯矩M和轴力N引起的附加剪应力以及剪力传递效率与所选取的截面位置、荷载作用方式和大小有关。周茂定等[18]运用比拟杆法，推导了波形钢腹板简支梁在荷载作用下的正应力计算公式。

从国内外的研究可以看到许多学者对剪切屈曲应力研究较多，并且通过实验的方法和有限元方法对剪应力的分布通常趋向于定性分析，但对变截面梁的剪应力研究还是相对匮乏，然而变截面梁作为一种最为经济的结构形式在大跨度桥梁中得到了广泛的应用。由于变截面的影响，变截面梁的剪应力计算公式和分布规律与等截面有所不同。因此，对这一问题的研究不仅具有理论意义，而且具有实践价值。本文对均布荷载作用下变截面波形钢腹板组合箱梁剪应力计算公式进行了推导，并对混凝土顶、底板和波形钢腹板中剪应力的分布规律进行了分析，本文的研究成果能为类似波形钢腹板连续箱梁剪应力分布与计算研究提供参考依据。

1 剪应力公式推导

(1) 基本假定

① 波形钢腹板梁与混凝土板截面在变形前后分别符合平截面假定。

② 波形钢腹板梁与混凝土板均为各项同性的弹性体，即应力-应变关系为线性关系，可应用叠加原理求解，混凝土在整个受力阶段未开裂。

③ 组合梁的竖向纤维无挤压，不考虑混凝土翼板的掀起，假定组合波形钢腹板梁与混凝土两者的挠曲位移完全相等，不考虑组合梁的横向变形，忽略波形钢腹板梁与混凝土板间的剪切滑移。

④ 在小变形条件下材料变形应服从Hooke定律。

⑤ 组合梁截面应力拉伸为正、压缩为负，弯矩以梁底受拉为正，受压为负。

(2) 变截面波形钢腹板剪应力分析

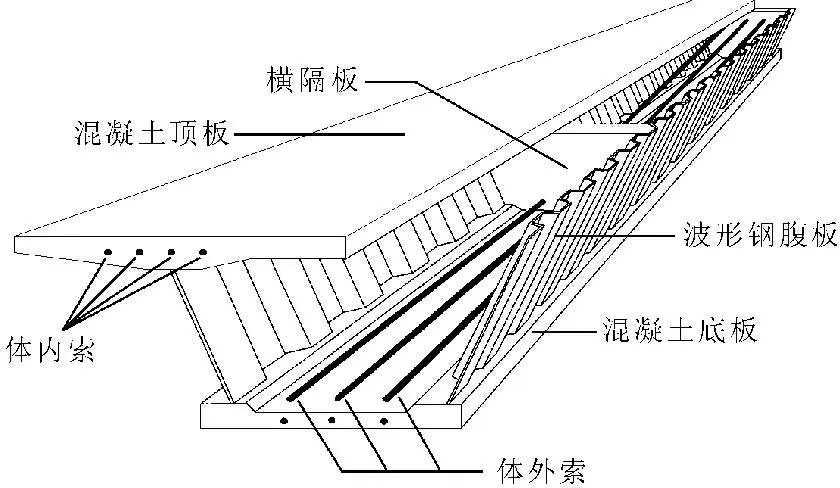
某一波形钢腹板组合箱梁典型截面如图2所示，设波形钢腹板顶板宽度b1、顶板厚度t1和底板宽度b2保持不变；在长度方向高度h、底板厚度t2、重心轴到顶板表面的距离zc是变化的。

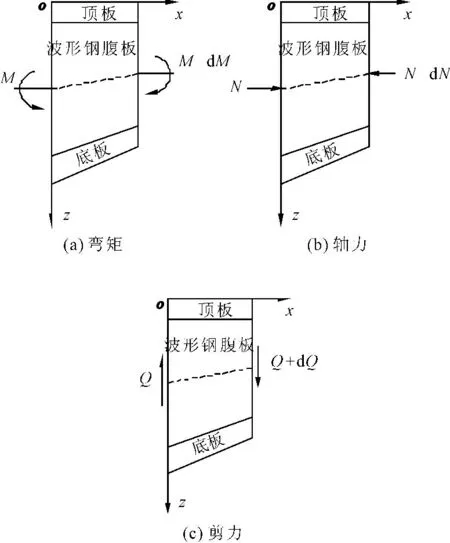
取一微段为研究对象，平面直角坐标系原点O取在顶板的上表面处，M、N、Q和q分别为作用在截面上的弯矩、轴力、剪力和均布荷载，图3(a)中两端横截面重心连线的水平倾角为θ，梁底的倾角为φ，变截面微段受力如图2所示，其中b1为顶板宽度，b2为底板宽度，t1为顶板厚度，t2为底板厚度，zc为微段上梁顶到重心轴的距离，z为任意位置距梁顶的距离，h为梁高。

由力矩平衡条件，可得：

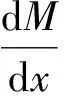
(1)

由假定①，根据材料力学公式可得微段横截面上距梁顶距离为z处的正应力表达为：

(2)

式中：A为微段横截面面积；I为微段横截面惯性矩。

规定式(1)、式(2)中底板受拉则弯矩为正，反之为负；如果剪力使微段有顺时针转动的趋势，则剪力Q为正，反之为负；如果微段处于压缩状态，则轴力N为正，反之为负；如果水平轴x沿顺时针旋转向中心线则θ为正，反之则为负。

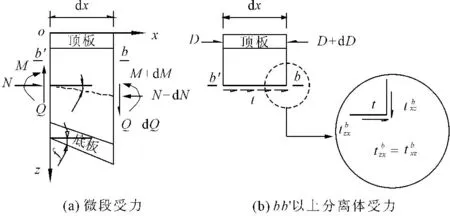
为计算横截面上任意一点b处的剪应力τ，取图3(b)所示的分离体作为研究对象，由x方向受力平衡可得：

(3)

式中：b(z)为计算点处的横截面宽度；D为计算点处以上部分所受的水平合力。

水平合力D作用于顶板上，其表达式为：

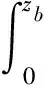
(4)

将公式(2)带入公式(4)得以下表达式：

(5)

式中：Aa为计算点以上部分的横截面面积；zb为梁顶到计算点之间的距离。

对公式(5)进行整理得：

zcAb-cAb=Sb

(6)

式中：c为面积Ab的重心到梁顶的距离，c≤zc；Sb为面积Ab对重心轴的静面距。

将公式(6)代入公式(5)得：

(7)

将公式(7)代入公式(3)中，结合偏微分方程，公式(1)和公式(7)中的轴向力N假定为常量。

(8)

公式(8)即为均布荷载作用下任意变截面梁剪应力计算的一般公式，可以看出变截面波形钢腹板箱梁剪应力由三部分组成：剪力引起的剪应力、轴力引起的剪应力和弯矩引起的剪应力，这三部分可简化为：

τ=τO+τN+τM

(9)

式中：τO为剪力引起的剪应力；τN为轴力引起的剪应力；τM为弯矩引起的剪应力。

(3) 截面几何参数的微分表达式

实际工程中波形钢腹板的厚度约为10 mm，由于折叠效应使得钢腹板的厚度对几何参数的计算影响很小，所以横截面上的A，I和zc可以写成：

A=b1t1+b2t2

(10)

(11)

(12)

忽略波形钢腹板的影响，假设顶板厚度不变，则A的变化率为：

(13)

(14)

令：

(15)

(16)

(17)

则式(14)可简化为：

(18)

计算阴影部分面积Ab与其静距Sb沿x轴的变化率时，须分以下三部分计算：

① 当剪应力计算点b位于顶板时(0≤z≤t1)

(19)

② 当剪应力计算点b位于腹板时(t1≤z≤h-t2)

(20)

③ 当剪应力计算点b位于底板时(h-t2≤z≤h)

(21)

(4) 变截面梁剪应力特性分析

从推导结果可以得到，均布荷载q作用下变截面波形钢腹板梁剪应力由剪力Q、轴向力N和弯矩M引起，实际剪应力是三部分叠加产生，以下对其进行单独分析。

① 弯矩M引起的剪应力分析(见图5(a))

将τM沿着截面高度进行面积分得：

(22)

将表达式(19)—式(21)代入式(22)，整理可得：

(23)

由式(23)知由弯矩M单独作用下产生的附加剪应力沿截面高度的积分为零，即弯矩产生的附加剪应力对总的剪应力没有影响。

② 轴向力N引起的剪应力分析(见图5(b))

将τN沿着截面高度进行面积分得：

(24)

将表达式(19)—式(21)代入式(24)，整理可得：

(25)

由式(25)知由轴力单独作用下产生的附加剪应力沿截面高度的积分为零，即说明轴力产生的附加剪应力对总的剪应力没有影响。

③ 剪力Q引起的剪应力分析(见图5(c))

将τQ沿着截面高度进行面积分得：

(26)

将表达式(19)—式(21)代入式(26)，整理可得：

(27)

由式(27)知剪力Q单独作用下剪应力沿截面高度的积分即为截面的剪力。

2 变截面悬臂梁算例分析

(1) 悬臂梁参数。选取文献[19]中一变截面波形钢腹板组合悬臂梁为研究对象，跨径为30 m，混凝土顶、底板宽度分别为4 m和2 m，腹板厚度为0.01 m，梁高从悬臂端部的2 m线性变化至悬臂根部的4 m，顶板厚度为0.3 m，底板厚度从悬臂端部的0.3 m按线性变化到悬臂根部的0.5 m，顶板上作用有q=300 kN/m的均布荷载，如图6所示，分别选择距悬臂端根部1 m、10 m、20 m、29 m处截面作为考察截面，依次标记为1#—4#号截面，如图6所示，材料参数见表1。

表1 材料参数表

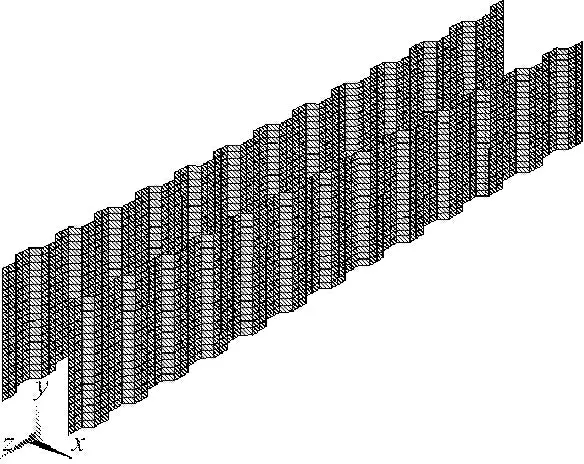
(2) 有限元模型的建立。采用大型有限元计算软件ANSYS 15.0建立上述变截面波形钢腹板组合梁的三维有限元模型，其中混凝土顶、底板采用实体单元Solid 45进行模拟，波形钢腹板采用壳单元Shell 63模拟，不考虑顶、底板与波形钢腹板间的层间滑移效应，波形钢腹板与混凝土顶底板间的连接采用MPC(多点约束方程)连接，该连接法可以不需要交接处的节点一一对应就能将不连续、自由度不协调的单元网格连接起来[20-21]，使得建模工作量大大减小，建模时先在实体单元表面建立Target 170单元，再在壳单元一侧建立Contact 175。悬臂梁根部约束梁体的竖向、纵向和横向3个方向的位移，有限元模型如图9—图11所示。

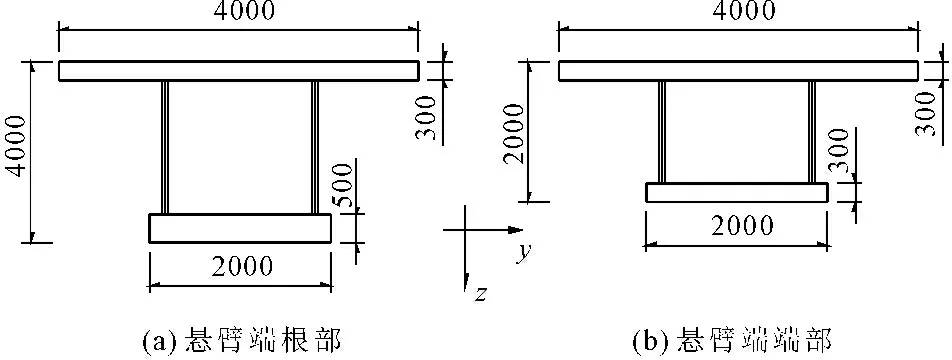
图7 截面图(单位：mm)

3 有限元结果与解析计算结果对比

将推导的变截面波形钢腹板剪应力公式计算所得结果与ANSYS有限元值进行对比，结果如表2所示。

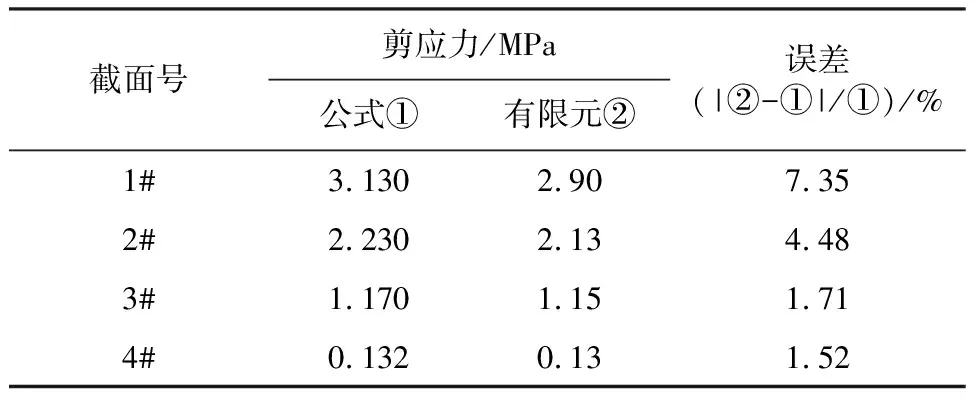
表2 各计算截面处波形钢腹板上的剪应力结果对比

由表2可知，本文公式计算所得的剪应力理论解与ANSYS三维有限元解吻合较好，说明了本文所推导的解析解的正确性，可以用于实际工程中变截面波形钢腹板组合箱梁剪应力的计算。

分析变截面波形钢腹板组合悬臂梁1#—4#截面的剪应力大小随箱梁截面到混凝土顶板上边缘的距离的关系，变截面波形钢腹板组合箱梁的剪应力用本文公式求得的理论解与ANSYS三维有限元值吻合较好。在中性轴以上区域剪应力的的变化规律先增大后趋于稳定，在中性轴以下先趋于不变后减小，中性轴以下的极值比中性轴以上的极值大。变截面波形钢腹板组合箱梁的剪应力的最大值出现在中性轴以下的某一点。

将1#—4#截面中性轴上下两侧的剪应力的极值进行对比，对比结果如表3所示。

从表3可以看出，变截面波形钢腹板组合悬臂梁1#—4#截面中性轴两侧的剪应力的理论解均大于ANSYS三维有限值。剪应力最大值的理论解和ANSYS三维有限元值在悬臂梁的固定端最大，从固定端到自由端依次减小。理论解在2#截面中性轴上下两侧剪应力极值的差值最大，达到了1.75%；ANSYS三维有限元值在1#截面中性轴上下两侧剪应力极值的差值最大，达到了8.39%。