装配式桁架钢筋混凝土叠合板-圆孔蜂窝组合扁梁力学试验研究

李维松，杨 睿，张九营，孟 娟，马全明

(1.徐州中国矿业大学 建筑设计咨询研究院有限公司， 江苏 徐州 221008； 2.徐州中国矿业大学 力学与土木工程学院， 江苏 徐州 221116)

建筑工业化和住宅产业化是世界性的大潮流和大趋势，也是我国改革和发展的迫切要求。装配式钢结构住宅自重轻、承载力高、抗震性能优越，建造周期短，钢材可回收利用，绿色节能环保[1]，符合住宅产业化的需要，是国家大力提倡的住宅发展方向。目前针对装配式钢结构住宅中的梁柱、梁板连接节点，国内外学者做了大量的试验和模拟[2-9]，提出了相应的计算方法和施工工艺。然而目前梁板节点施工时需要大量现场焊接、钢筋绑扎和混凝土浇筑等作业，降低了施工效率，组合梁翼板作用在钢梁上翼缘，降低了建筑净高，且钢梁外漏，防火防腐处理复杂，因此研究新型梁板连接节点具有重要意义。桁架钢筋混凝土叠合板广泛应用于装配式混凝土结构中，相关图集标准健全，生产技术成熟，是国家大力推广的技术。蜂窝钢梁具有力学性能良好、用料节省、外形美观以及经济效益显著等特点，在工业与民用建筑中用途较广。将叠合板与蜂窝梁组合，叠合板作用在钢梁下翼缘形成装配式桁架钢筋混凝土叠合板-蜂窝组合扁梁(如图1所示)，由于钢梁开孔能够节约钢材、减轻自重又方便管线、楼板钢筋的穿越，组合扁梁能增加楼层净高，提高组合结构的整体性能和耐火、耐腐蚀性能。

本文通过两组装配式桁架钢筋叠合板——蜂窝组合扁梁试件的力学试验，对其承载能力、变形能力、破坏规律等方面进行分析和研究，为装配式桁架钢筋叠合板-蜂窝组合扁梁的设计和工程应用提供理论依据。

1 试验概况

1.1 试件设计

叠合板配筋参考图集《桁架钢筋混凝土叠合板(60 mm厚底板)图集》[10](15G366-1)，预制底板厚60 mm，现浇叠合层厚70 mm，标志跨度4 000 mm，标志宽度2 400 mm，底板跨度方向配筋为Φ8@150。参照文献[11-12]，兼顾叠合板的力学性能、加工和运输条件，综合确定组合扁梁的有效翼缘宽度为800 mm，叠合板的宽度为325 mm。蜂窝梁选取两种较常用的截面，高度分别为200 mm(SD1)和250 mm(SD2)，上翼缘宽度150 mm，下翼缘宽度200 mm，断面图如图2所示，侧视图如图3所示。叠合板混凝土等级为C30，钢筋均为HRB400级，钢梁及其他钢构件均为Q345。

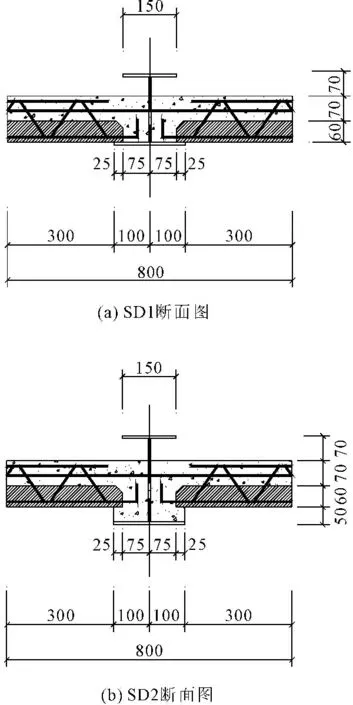
组合扁梁两端支座处及集中力加载点处设置加劲肋，支座处加劲肋兼具防止蜂窝梁与混凝土板滑移的作用。为增强混凝土板与蜂窝梁的协同工作，防止界面滑移，在蜂窝梁孔内布置负筋和构造钢筋，穿过蜂窝梁孔的负筋及构造钢筋分别为Φ10@200和Φ8@200。

1.2 加载装置和加载方案

装配式桁架钢筋叠合板-蜂窝组合扁梁两端简支，压力机(作动器)作用在跨中，通过分配梁将两个竖向荷载传递到试验梁，竖向荷载作用在试验梁三分点处，在梁加载点上翼缘放置滚轴和固定支座。放置试件、分配梁和支座时注意与作动器以及支墩的中心线对中，避免分配梁或者试件偏移或两端不对称，防止加载过程中过早发生平面外失稳或局部失稳，影响试验效果。加载采用分级加载的形式，第一级从15 kN开始，此后每级递增15 kN，为保证所施加荷载充分传递到试件上，每级荷载加载持续5 min，达到加载值时持荷3 min，进行读数，在接近混凝土板开裂荷载时减缓加载速率，采用半级加载，观测混凝土裂缝和试件变形的发展，直至试件破坏(当荷载下降到试件极限荷载的85%或板上部混凝土被压碎或板钢筋拉断时，即认为构件破坏)。

1.3 量测方案

荷载测量：组合扁梁上荷载通过其内置传感器记录，并在控制台显示器上实时显示。裂缝测量：在试件混凝土出现裂缝后，利用裂缝观测仪观察裂缝的数量、宽度和变化，裂缝出现后每一级加载后记录裂缝最大宽度，并在试件上用红色记号笔描绘裂缝变化，标明荷载级别。挠度测量：在组合扁梁的钢梁上沿长度方向上4等分点共放置5个位移计以量测组合扁梁各点实时挠度。其中为防止支座沉降对试件挠度值产生影响，在两端支座处上翼缘各放置一个位移计，用以观测支座位移，5个位移计从左至右依次编号1—5。在叠合板端部预制部分和现浇部分截面中点各布置一个位移计，用以监测加载过程中叠合板和现浇层界面的滑移量，位移计布置如图4所示。应变测量：应变片及应变花的布置参考文献[13]进行布置，见图5。(1) 在两根蜂窝梁支座附近沿梁截面高度等距(SD1标距80 mm，SD2标距100 mm)布置3个电阻应变片记录沿梁截面高度方向的应变变化；(2) 弯剪段加载位置右侧第一个孔周围45°及135°方向上布置4个45°直角电阻应变花，记录加载过程中应变变化数值，用于计算相应位置处的主应力；(3) 由于纯弯段仅有正应力产生，仅在跨中纯弯段的孔上部各布置一个电阻应变片，用以记录试验过程中的应变变化情况。混凝土板应变片参考文献[2,11]在跨中截面两侧混凝土板的顶面沿板宽度方向等距布置3个应变片，用以记录混凝土板沿宽度方向的应变变化情况布置，见图6。

2 主要试验结果

试件SD1、SD2的破坏过程基本相似，SD1破坏过程如图7所示，SD2破坏过程如图8所示。首先当输出荷载较小时，试件的跨中挠度呈线性变化，处于弹性阶段，试件没有明显变形和裂缝。当荷载逐渐增大，在钢梁没有明显变形的情况下，叠合板跨中底部首先出现裂缝，且裂缝逐渐增多并向叠合板侧边发展，试件挠度逐渐增大，且幅度逐渐加快，当荷载达到某一数值后，作动器显示器上力-位移图像开始由直线转为曲线。当叠合板发生破坏时，立即暂停加载，试件承载力还没有下降，但混凝土板已经破坏，试件没有明显的局部变形和扭曲、失稳，叠合板与现浇层的裂缝连续，界面没有发生肉眼可见的滑移，但混凝土板与钢梁两端部下侧连接界面可见少部分脱开，出现缝隙。试验结束时SD1、SD2荷载显示分别为554.9 kN、765.6 kN，叠合板跨中底部最大裂缝宽度分别为7.04 mm、7.54 mm，跨中最大挠度分别为92.77 mm、91.09 mm。

3 试验分析

3.1 荷载-应变曲线

利用GBD3816应变数据采集仪采集试验过程中梁截面各处的应变数据，并绘制出蜂窝钢梁荷载-应变曲线图，见图9、图10。结果表明，在加载的弹性阶段，两组试件的应变值呈线性增长，当预制叠合板组合扁梁构件屈服之后，虽然作动器输出荷载增长速度减缓，但荷载-应变图像呈现曲线增长，应变值增长加快。沿梁高度方向的应力和应变呈现中间小，向两端增大的变化趋势。由于叠合板的作用，组合扁梁中和轴下移，弹性阶段SD1试件2号应变片数值为负，表明此处为压应力。SD2试件由于叠合板基本上位于钢梁中间位置，中和轴位置变化不大，故2号应变片数值很小。叠合板上表面沿宽度方向荷载-应变曲线见图11，在弹性阶段，混凝土翼板上表面的应变增长缓慢，试件屈服之后，叠合板应变增长加快。沿板宽度方向应变分布较均匀，内部较大外部较小，但差值不大，有效翼缘宽度选取比较合理。

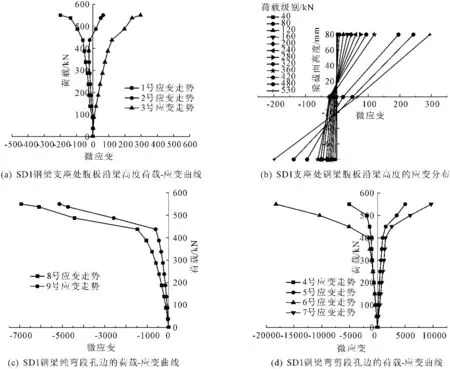
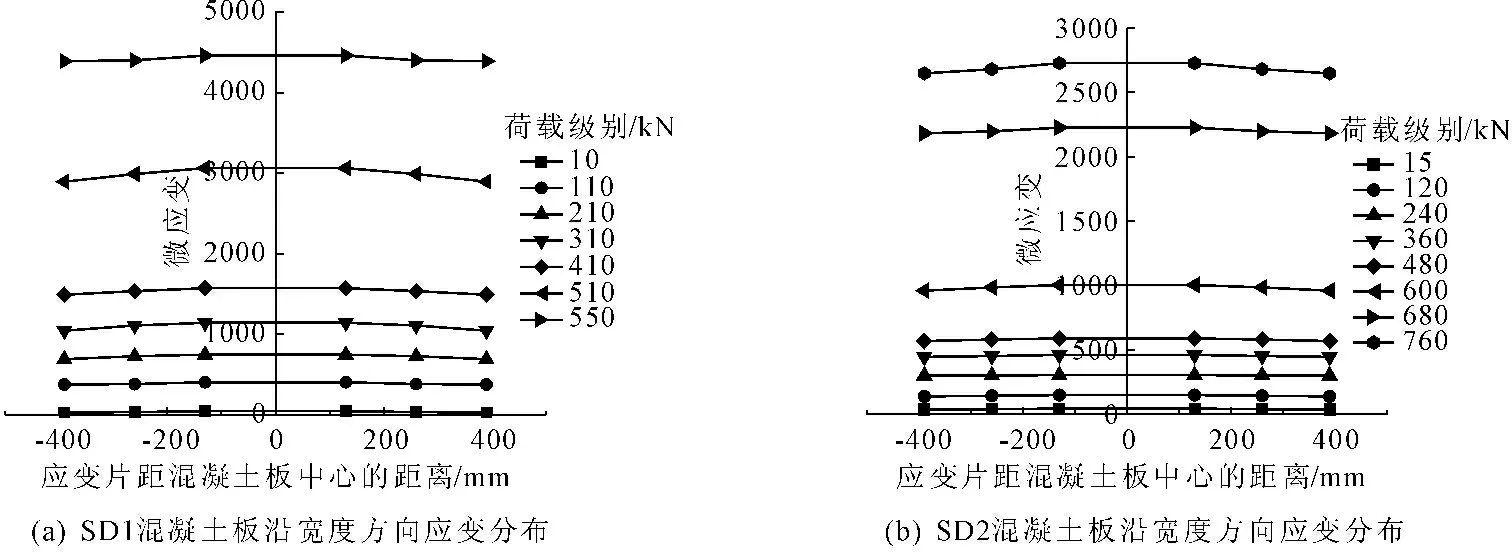
图11 SD1、SD2试件混凝土翼板沿宽度方向应变

3.2 承载能力分析

两组组合扁梁试件的屈服荷载、破坏荷载对比如图12所示。

根据文献[14]所给出的式(1)、式(2)、式(3)计算蜂窝梁弯矩和剪力设计值，其中弯矩设计值取公式(1)、式(2)计算结果的较小值，计算值与试验值对比如表1所示。

(1)

M≤fhzAt

(2)

(3)

式中：M，V为蜂窝梁截面弯矩及剪力设计值；W1为梁墩处实腹截面模量;f、fv分别为钢材抗弯、抗剪强度设计值；h2为桥部上下T形截面的重心距；At为桥部T形截面面积；S、I为支座截面对中和轴的面积矩和惯性矩；tw为钢梁腹板厚度。

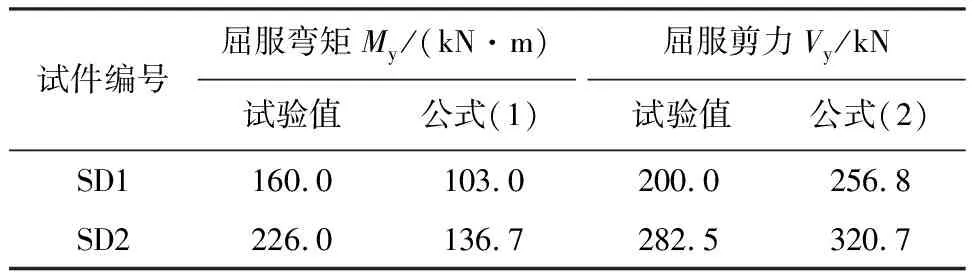
表1 SD1、SD2试件试验值与理论值对比

由表1数据可知，钢梁屈服时，试验所得弯矩值分别要比公式计算值提高了20%、60%，由于组合扁梁的混凝土包裹住钢梁的部分腹板，填充了腹板的孔洞，且翼板的受压区混凝土和钢筋与钢梁共同作用，比蜂窝梁具有更好的抗弯能力。钢梁屈服时，剪力试验值比公式计算值分别要小21.1%、13.2%，约为其计算值的0.8倍，组合扁梁的屈服由抗弯承载力控制，此时的剪力并未达到屈服极限。

《混凝土结构设计规范》[15](GB 50010—2010)3.4.5条，一类环境下混凝土板裂缝缝宽度限值为0.30 mm。根据试验，SD1试件在跨中弯矩达到72 kN·m、SD2试件在跨中弯矩达到132 kN·m时，板最大裂缝仍未超过限值。

3.3 荷载-跨中挠度曲线

SD1、SD2试件的屈服荷载、破坏荷载及相应的位移如表2所示，荷载-跨中挠度曲线如图13所示。从图13中可以看出，两个试件在加载弹性阶段，荷载-跨中挠度曲线都保持较好的线性，进入屈服之后，荷载增长开始缓慢，挠度却加速增加，图像开始由线性变为曲线，斜率不断减小，但直到试件叠合板部分破坏，两个试件都未达到承载力极限。通过位移计读取结果，可以直观地看出各加载阶段SD1、SD2试件的受弯变形情况，如图14所示。

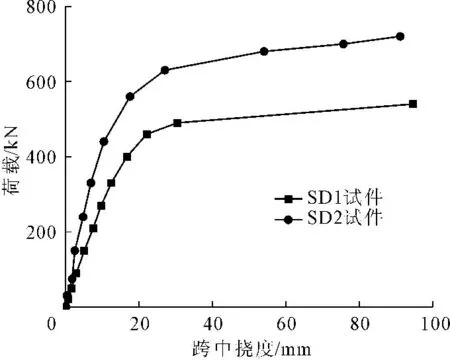
表2 SD1、SD2试件的屈服荷载、破坏荷载及相应的挠度

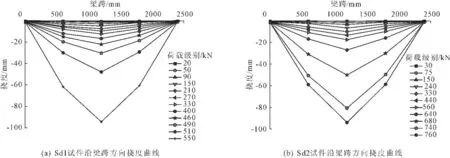
图14显示了试验梁在加载各个阶段各点的挠度变化情况，在试件跨中左右两侧的挠度为对称关系。在弹性阶段，两组试件挠度增长幅度较小，且变化比较均匀，试件屈服之后，梁中各点的挠度开始迅速增加。整个加载过程中试件两端支座处位移计很小，影响可以忽略不计。在叠合板端部预制部分和现浇部分截面中点各布置的位移计在加载全过程的差值始终未超过0.18 mm，可以认为叠合板与现浇层界面没有明显滑移，连接可靠。

根据文献[14]，蜂窝梁挠度计算公式见公式(4)。

(4)

式中：Mkmax为跨中最大弯矩标准值；l为蜂窝梁的跨度；E为钢材的弹性模量；I0为当量实腹梁截面惯性矩；η为考虑空腹截面影响的增大系数，其经验取值为1.4，SD1和SD2试件的试验挠度结果与原实腹组合梁公式计算结果的对比如见表3。

表3 公式计算与试验结果对比

分析得知，两组组合扁梁试件的试验实测的挠度值均比蜂窝钢梁理论计算的挠度值小，这是由于组合梁混凝土翼缘板的有利作用，假定α为考虑组合扁梁翼缘板影响的挠度折减系数，由表3计算得知该折减系数为0.5。本试件的挠度容许值[16][v]=l/400=6 mm，从试验结果可知，试件SD1在所受荷载达到150 kN、SD2试件达到240 kN时才接近限值。

3.4 延性

构件或者整体结构从屈服到极限承载能力或到达以后而承载能力还没有明显下降期间的变形能力，称为延性。本文中试验结束时试件承载力还未下降，但叠合板已经破坏，实质上已经达到极限承载力，故仍采用位移延性系数μΔ=Δu/Δy分析两组组合扁梁试件的截面延性，计算结果如表4所示。

表4 SD1、SD2试件位移延性系数

试验表明，组合扁梁具有相当好的延性，整个加载过程中，由于梁板组合作用使得试件保持良好的整体性和稳定性，避免了试件局部屈曲和失稳，且钢梁与混凝土界面、预制叠合板与现浇层界面没有明显滑移、脱离，组合结构整体变形一致，混凝土板裂缝贯通，上下连续，没有发生脆性破坏，试件拥有良好的变形能力。

4 结 论

(1) 试件SD1、SD2的破坏过程都经历了弹性、弹塑性、塑性三个阶段，叠合板破坏时，SD1、SD2试件的承载力还在继续上升。

(2) 在钢梁屈服之前，两组组合扁梁上沿截面高度方向上的应变基本沿梁高度方向直线分布。

(3) 组合扁梁屈服时，弯矩试验值比公式计算值提高了约20%～60%，组合扁梁比蜂窝梁具有更好的抗弯能力。剪力试验值约为公式计算值的0.8倍，组合扁梁的屈服由抗弯承载力控制，此时的剪力并未达到屈服极限。组合扁梁的试验实测的挠度值比蜂窝钢梁理论计算的挠度值小，计算得出考虑组合扁梁翼缘板影响的挠度折减系数α为0.5。

(4) 蜂窝梁与叠合板通过钢筋和现浇层连接成一体，翼板给钢梁提供稳定的侧向支撑和约束，且各项构造措施效果良好， SD1、SD2试件在整个加载过程中几乎没有出现局部屈曲、平面外失稳以及现浇层与叠合板之间的脱离和滑移的现象，裂缝贯穿和发展都比较连续，有较好的整体性和变形能力。