椭圆加密算法的改进算法研究与分析

王玲丽

摘要：随着移动互联网技术、物联网、电子商务等各种应用的急速发展，针对计算机安全、网络安全、信息安全的威胁越来越严重，信息安全的重要性越来越得到人们的重视，椭圆曲线加密技术目前在TLS、PGP和SSH等中应用广泛，在有限域 GF（p）上包括椭圆曲线点加法运算及其可视化，在有限域 GF（p）上椭圆曲线标量乘法运算及其可视化，椭圆曲线点对实数域 R的加法运算及其几何意义，都将在本论文中展开研究。

关键词：椭圆曲线;椭圆曲线加密;可视化工具;加密与解密

中图分类号：TP311      文献标识码：A      文章编号：1009-3044（2019）01-0054-03

本文主要是研究在安全性、计算效率方面有很大优势的一种公钥密码[1]体制——椭圆曲线加密算法及其应用。其研讨工作主要有以下几个方向：HTML5+ jQuery框架 Web前端开发技术，椭圆曲线加密算法与数学有着密切的关系，尤其是对在有限域上的椭圆曲线形成的循环子群[2]、生成元的生成算法进行了详细的研究，因为它们对于实际的 ECC加密算法的实现非常关键。相关的算法和实现细节也在论文中进行了展示;并改进了双点计算的方法[9]，从而提高了椭圆曲线密码的加密和解密过程的速度。点nP的标量运算的时间复杂度从O（n）提高到log（n）。

1 椭圆曲线群运算及可视化工具开发

椭圆曲线加密一直都广泛地在TLS、PGP和SSH中运用。椭圆曲线加密算法在数学领域中也可以灵活运用，例如椭圆曲线几何、集合论、阿贝尔群、有限域等。这些运算不仅抽象，而且计算量也很大。故本文利用HTML5和css、jQuery框架等相结合的想法，利用研究有限域椭圆曲线的可视化工具进行开发研究。

1.1 椭圆曲线的可视化工具的开发

为了更好地理解椭圆曲线上的点的各种操作及其几何意义，有必要直观地理解椭圆曲线，例如奇异曲线。 因此，本文开发了实际场和有限域中的椭圆曲线可视化工具软件。 b的值在真实场上给出了各种不同的椭圆曲线。

1.2 椭圆曲线Abel群的定义及几何意义的可视化

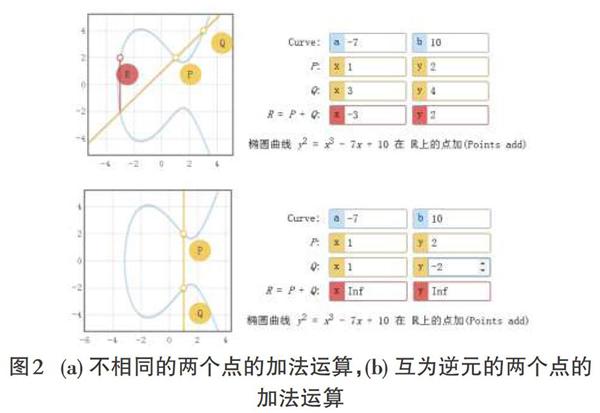
为了点加运算更加清晰地展现出来，本文开发了可视化工具软件显示其代数计算的结果以及其几何意义：椭圆曲线连接到两个不同点P和Q的和，并且PQ的延长线和曲线相对于x轴的交点称为椭圆的切线。 图1-2（ a）是椭圆曲线上的两个点 P（1，2）， Q（3， 4）相加得到点 R（-3，2）以及其几何意义，点 R（-3， 2）是 PQ延长线和椭圆曲线的交点（-3，-2）的对称点。 图1-2（a）还验证了椭圆曲线下的组的定义： 在椭圆曲线上，三个非单位点 P， Q，- R以直线连接，并且它们的和为 P+ Q+ （- R）= O.图1-2（ b）说明了在椭圆曲线上定义组的另一个规则： 若 P、 Q互为逆元，即 P与 Q关于 x轴对称或者说 Q=- P，则 P+ Q= O，它也表达了一个无限点。

标量乘法也称为双点运算，即计算。当变量n很大时，计算的时间复杂度也会变大。 图1-3（a）是椭圆曲线上不相同的两个点的相加; 图1-3（ b）显示了两个相互反向元素的点的相加，即通过该点的椭圆的正切，切线和椭圆曲线交点处的对称点是添加两个相同点的结果; 图1-3（ b）和1-3（ c）表示添加两个相同的点（ P+ P）具有点 P的双标量乘法（2 P）的结果在几何上是一致的。

1.3 有限域GF（p）上椭圆曲线群点集的计算

假设有椭圆曲线[E97（2，3）：y2=x3+2x+3（mod97）]，其上有 P（3，6），如果在 P上执行标量乘法计算，你会发现结果只有五个不同的值（ O， P，2 P，3 P，4 P），并且循环出现。 可以证明的是纯量乘法在加法运算下是出于封闭状态下的，换句话说，通过在有限域上的椭圆曲线的点 P上迭代地执行标量乘法而获得的一组点构成循环子组。 P称为循环子群的生成元（ generator）或基元（ base point）。

子群的阶：由P生成的椭圆曲线上的子群的阶是指一个最小的正整数n，满足nP=O。例如在图1-4中，椭圆曲线[E97（2，3）：y2=x3+2x+3（mod97）]上的一个点P（12，3）生成的子群的阶是50。

因此，在有限域上GF（p）上橢圆曲线两个点相加P+Q=R的几何意义是：首先由P、Q确定斜率为m的一组平行线（满足线性方程y=mx+c （mod p）），如果椭圆曲线的点集合中的某个离散点R落在某一条平行线上，则R关于x轴的对称点R就是P+Q的计算结果。例如在图1-5中，椭圆曲线C上的两个点P（16，20）， Q（41，120）进行点加运算，计算斜率C，c=83，得到满足方程C的一组平行线，在点集合中容易验证R=（86， 46）满足该方程，则R的逆元R=（86， -46）=（86，-46+127）=（86， 81）即为点P与Q相加的结果。

2 椭圆曲线加密算法的改进与优化

2.1 对椭圆曲线群纯量乘法的优化与改进过程

除了进行点加法之外，还有另外一种运算叫点乘运算[4]：cP=P+P+...+P，其意义为计算cP需要执行n-1次加法，其点乘运算的时间复杂度为O（n）。如果用k位二进制表示，即c=bk-1…b1b0，则算法的时间复杂度为O（2k），可以利用倍加运算（double and add operations.）进行快速计算，如果n表示为二进制，则该二进制表示可以转化为2的幂和。然后，我们取n的每一个二进制数，乘以它的2次方。

[n=i=0…k-1bi?2i]

（1） 若倍加操作的运算为O（1），则该算法的复杂度为O（logn），运用此优化改进之后其复杂度O（n）。计算151P，则将151用二进制表示则为100110111，151P=（1*27+0*26+0*25+1*24+0*23+1*22+1*21+1*20）P，最终计算出151P的结果需要通过7次的“加倍运算”与4次“相加运算”即可实现，运算的时间复杂度明显降低。

（2） 给定一个有限域椭圆曲线，要利用其实现椭圆曲线加密算法，那么椭圆曲线群生成元P的选择及其阶的计算至关重要。本文中采用的方法不是首先选择一个生成元，然后计算基于该生成元的子群，而是寻找一个生成元使其生成的循环子群具有高阶。所采用的方法如下：

① 选择一个椭圆曲线Ep（a，b）： y2=x3+ax+b mod p;

② 计算该椭圆曲线的阶N;

③ 如果G=hP是单位元O，则转到第（4）步重新选择一个点P，否则就找到了一个具有阶n和辅因子h的循环子群的生成元G=hP。

（3） 例如，根据本文在第4章开发的可视化工具的计算，椭圆曲线y2=x3?x+3 （mod 37）的阶为N=42，N的因子有n=1 ， 2， 3， 6， 7， 14， 21，42，选择n=7（素数）作为子群的阶，随机选择椭圆曲线的一个点P=（2， 3），h=N/n=42/7=6，计算hP=6P=（2，34）≠O，因此得到用于椭圆曲线加密的循环子群，其生成元是G（2， 34），阶为n=7。

2.2 椭圆曲线加密解密算法

2.2.1 ECC的密钥生成算法

假如通信双方为A，B，发送方为A，接收方为B，要生成一个用户B的公钥、私钥对的算法如下：

（1） 选择一个椭圆曲线E：y2=x3+ax+b（mod p），构造一个椭圆Abel群Ep（a， b）;

（2） 在Ep（a， b）中挑选生成元G=（x0，y0）， G应使得满足nG=O的最小n （n是G的阶）是一个非常大的素数;

（3） 选择一个小于n的整数nB作为私钥，公钥为PB=nBG， 即：

用户B的public key=（n， G， PB， Ep（a， b））。

用户B的secure key=nB（小于n）。

2.2.2 AàB实现保密通信，发送端A的加密算法

step1：将明文消息编码成一个数m<p，将m镶嵌到曲线上得点Pm=（xm，ym），再对点Pm做加密变换。

step2：在[1， n-1]内选取一个随机整数k， 计算点P1=kG。k是保密的，但接收端无须知道。

step3：根据B的公钥PB， 计算点P2=kPB。

step4：A端传送加密数据Cm={P1， Pm+P2}，其为2个点。

2.2.3 AàB实现保密通信，接收端B的解密算法

step1：接收方B接收到的是2个点kG， Pm+kPB ，其用自己的私钥nB做如下计算：Pm+P2- nBP1即可解密，因为Pm+kPB- nBkG= Pm+knBG- nBkG=Pm。

step2：根据Pm，接收端再根据发送方的明文编码的镶嵌方法即可得到明文编码m，进一步得到明文。

2.3 椭圆曲线加解密算法的实现与结果分析

椭圆曲线密码体制是基于有限域GF（89）上的E89（-1，0）： y2=x3-x mod 89，根据文献 [3]中的Schoof算法计算该椭圆曲线群的阶为N=80，N的所有因子为n=1， 2， 4， 5， 8， 10， 16， 20， 40， 80。对于N的每个因子n=1， 2， 4， 5， 8， 10， 16， 20， 40， 80，计算nP。

1P=（68，4）， 2P=（21，42）， 4P=（68，85）， 5P=O， 8P=（21，47）， 10P=O， 16P=（68，4）， 20P=O， 40P=O， 80P=O。

易知，满足nP=O的最小的n=5且其为素数，计算其协因子h=N/n=16。随机选择椭圆曲线上一个P（12，5）且满足hP=16P=（68，85）≠O，则选择G=（68，85）作为用于椭圆曲线加密的循环子群的生成元。很显然其阶为n=5，因为nG=5G=5*16P=80P=O。

选择小于n的整数dB=3作为接收端B的私钥（Private Key），计算B的公钥（Public Key）PB=dBG=3（68，85）=（21，42）。

發送端A加密时选择一个秘密整数k=2，对明文消息“hello！”的加密过程及加密结果（密文）如下：

[明文 编码 分组m 将m映射到椭圆曲线上的点Pm（xm， ym）， 取r=30， j=0…r-1 加密结果={P1，P3}，k=2.

P1=kG=2（68，85）=（21，47）， P2=kPKB=2（21，42）=（68，85）

P3=Pm+P2=Pm+（68，85） h 68 26 （77， 8）， j=9 {（21，47），（15，45）} e 65 06 （12， 5）， j=10 {（21，47），（51，41）} l 6c 21 （17， 1）， j=10 {（21，47），（72，55）} l 6c 44 （1， 0）， j=16 {（21，47），（15，45）} o 6f 27 （37， 8）， j=28 {（21，47），（65，66）} ！ 21 06 （12， 5）， j=10 {（21，47），（51，41）} 60 （37， 8）， j=17 {（21，47），（65，66）} 33 （25， 5）， j=14 {（21，47），（32，42）} 密文{（P1，P3）} （21，47）（15，45），（21，47）（51，41），（21，47）（72，55），（21，47）（15，45），（21，47）（65，66），（21，47）（51，41），（21，47）（65，66），（21，47）（32，42） ]

一个明文分组映射为椭圆曲线上的点加密之后的密文是两个椭圆曲线的点，因此椭圆曲线加密传输的效率为50%。

3 结论

虽然还有很多不足，并且已经提出了大量的隐私保护方法，但仍然需要更多的研究，有许多挑战需要克服。其中最重要的可能是对用户隐私的适当保护的ECC算法。因此，本文提出改进了ECC的精确度，并使得椭圆曲线密码的加密和解密过程的速度得到提高、点的纯量乘法nP的计算时间复杂度提高，并力争达到工业级别的ECC加解密教学演示系统、数字签名教学演示系统。

参考文献：

[1] Carron， L.P.， Morse Code： The Essential Language. Radio amateur's library. Vol. 69. 1986： American Radio Relay League.

[2] 于伟. 椭圆曲线密码学若干算法研究[D].中国科学技术大学，2013.

[3] R. Schoof： Elliptic Curves over Finite Fields and the Computation of Square Roots mod p. Math. Comp.， 44（170）：483–494.Available at http：//www.mat.uniroma2.it/～schoof/ctpts.pdf

[4] 陈少云.拉格朗日中值定理的应用实例[J].河南教育学院学报（自然科学版），2017，26（3）：54-57.

[5] Chengwei Wang. Linear singular blending rational spline curve[P]. Computing， Control and Industrial Engineering （CCIE）， 2011 IEEE 2nd International Conference on，2011.

[6] 劉建成，杨晓静，张玉.基于改进欧几里德算法的（n，1，m）卷积码识别[J].探测与控制学报，2012，34（1）：64-68.

[7] 刘丽涛，王刃峰.基于JavaScript+jQuery的网站设计与实现[J].电脑编程技巧与维护，2018（8）：40-41+53

[8] 易泽顺. 基于Web的数据可视化工具设计与实现[D].华中师范大学，2017.

[9] 李明. 椭圆曲线和超椭圆曲线上标量乘的快速计算[D].山东大学，2012.

[10] 张晓军.基于HTML5+CSS3.0+jQuery在移动电商APP开发中的应用[J].通讯世界，2015（6）：57.