一种基于形态分量的多聚焦图像融合算法
2019-03-14张杰敏
陈 杰,茅 剑,张杰敏
(集美大学计算机工程学院,福建 厦门 361021)
0 引言
图像融合是以图像为对象的信息融合的研究方向,其目的是将多个不同或相同类型的传感器在同一时间或不同时间获取的关于某个场景的多幅图像信息加以综合,从而产生新的有关此场景解释的信息处理过程。通过对多幅传感器图像的融合可克服单一传感器图像在几何、光谱和空间分辨率等方面存在的局限性和差异性并提高图像的质量,有利于对物理现象和事件进行定位、识别和解释[1]。
由于镜头景深的限制,当所拍摄的物体与镜头的距离相差较大的情况下,现有的摄像头无法聚焦所拍摄的所有物体。多聚焦图像融合是解决当前问题的方法之一。多聚焦图像融合能将对聚焦在不同位置的图像融合成为一幅图像,从而提供更为清晰的图像,以此表示更准确和可靠的内容,便于人的观察或机器的后续处理。图像融合为人或机器后期的图像处理提供了便利的条件,因而在遥感图像、航天航空、公安安防、工业设计等领域中获得了越来越多的应用[1-2]。
目前,图像融合算法主要分为空域和变换域两大类。空域融合算法的主要特点是将带融合的图像进行分块并逐块比较或逐像素点比较,通过空间频率、拉普拉斯能量、梯度算子等检测分块的清晰度,从而选择具有较高清晰度的图像分块或像素点用于融合后的图像[3]。变换域图像融合算法基本是对图像进行变换,然后对不同的变换系数采用不同的融合规则进行融合,最终得到融合后的图像。目前,变换域多聚焦图像融合算法主要有基于DCT变换[4-5]、小波变换[6-9]、curvelet变换[10-12]、contourlet变换[13-14]、金字塔分解[15-16]等方法。
当前主要的多聚焦图像融合算法都是将图像作为单一分量来进行表示,这也意味着它们在表示图像内容信息的时候具有一定的局限性。如果能将图像分解成多个不同的分量,那么图像内容的表示将会更有效和更完整。
稀疏表示[17]是指一幅图像可由一个过完备字典中少数几个原子图像来线性表示。使用稀疏表示可以使图像的能量集中在少数的原子图像上,而这些原子图像同时也反映了待表示图像的主要特征和基本结构。curvelet变换是一种基于多尺度的图像分析工具,与小波变换相对比,由于curvelet变换的基支撑区间具有各向异性的特点,因而curvelet变换可用能量更加集中的稀疏的系数来表示图像边缘、纹理等细节信息,特别是能够对奇异曲线进行最优的稀疏逼近表达,因此可以更方便地对图像特征进行分析[18-20]。curvelet因其良好的特性使其在去噪、图像增强、图像恢复等许多领域都得到了广泛的应用[21-23]。Starck等[24-25]提出的形态分量分析(morphological component analysis,简称MCA)就是采用curvelet对图像进行分解的,他们认为图像的低频和高频可以用不同字典来稀疏表示,是一种对图像进行分解的方法。
本文根据稀疏表示的特点,使用迭代分解的方法将待融合的源图像进行分解,得到源图像的低频分量和高频分量。随后,对分解后的低频分量和高频分量根据不同的特点制定不同清晰度以便判定,并用于最终的融合,最后将融合后的低频分量与高频分量合并,以期得到真正融合后的结果。
1 稀疏表示与curvelet变换
设x是n维信号,
(1)
其中Φ={φ1,φ2,…,φn}称为字典,α={α1,α2,…,αn}是Φ的系数表示。若x是n维向量,L≫n,则称Φ={φ1,φ2,…,φn}是一个过完备字典。找出信号x的最稀疏表示,即α中非零元最少的情况:
(2)
以多分辨率为核心的小波变换克服了傅里叶变换在图像处理上的不足,因此得到了广泛的应用[26]。但是由于二维的小波变换是由一维的小波变换所推广得到的,因此小波变换图像上仍然只能描述图像的点奇异性,而无法描述线奇异和面奇异等高维信号特征。此外,由于小波描述的是水平、垂直和对角线三个方向的特性,而对于边缘等多方向的图像特征无法得到较好的描述[17]。
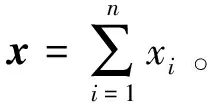
x=xC+xT=ΦCαC+ΦTαT。
(3)
2 基于形态分量的图像融合算法
2.1 图像融合框架
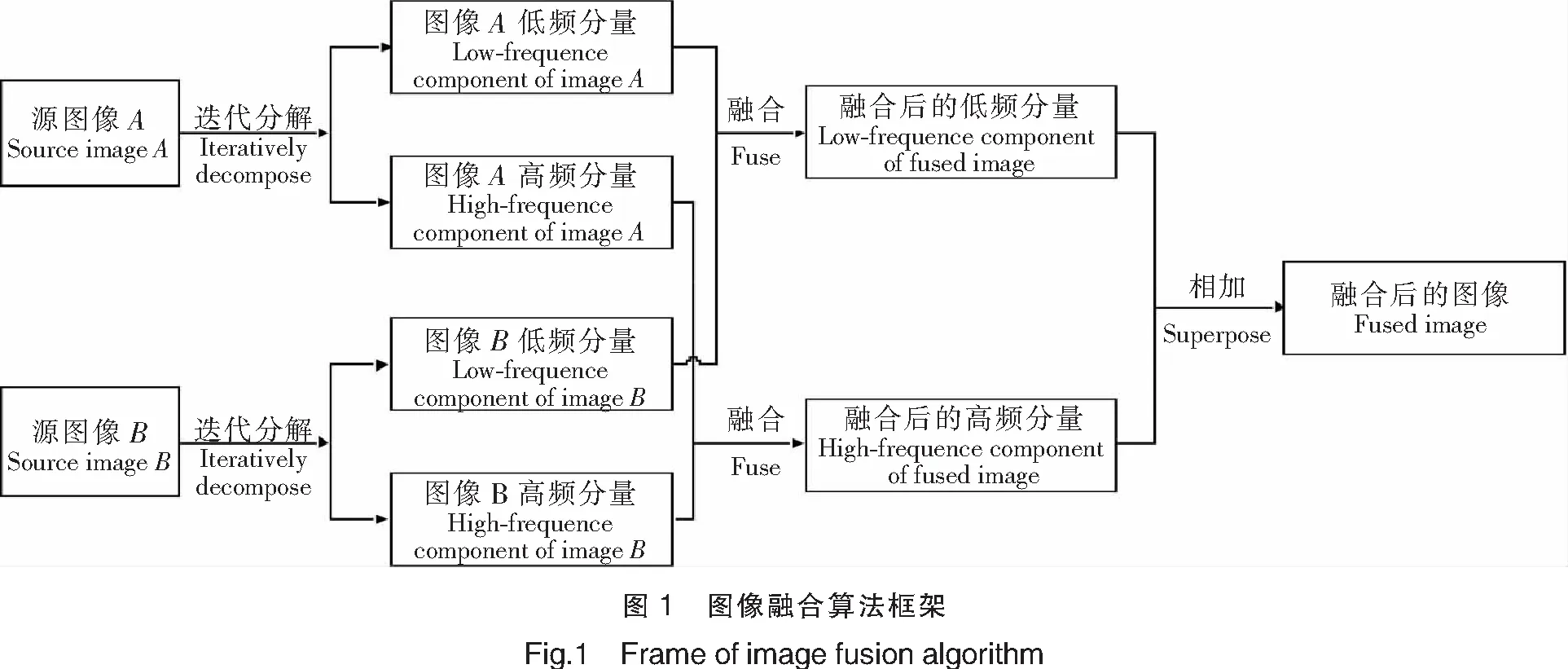
本文图像融合算法的过程主要由“分解—融合—相加”三个部分组成。融合算法框架如图1所示。
分解:基于稀疏表示的特点,将待融合的源图像迭代分解,并使用字典表示分解后的低频分量,同时将原图像减去低频分量,得到高频分量。
融合:根据低频和高频分量的不同特点,定义不同的清晰度规则,并将其用于融合处理,从而得到新的低频分量和高频分量。
相加:将新的低频分量和高频分量合并,得到最终的融合后的图像。
2.2 迭代分解
图像的迭代分解使用Starck等[24-25]的思想方法,使用curvelet变换和滑动重叠窗口的局部离散余弦变换分别作为低频分量和高频分量所表示的字典,具体分解算法如下:
输入 原始图像I0

输出 图像低频分量I1,高频分量I2
Step1 定义最大阈值λmax和最小阈值λmin,低频系数融合规则,初始化I0为原始图像,I1=0,I2=0,初始化迭代次数N,阈值δ=λmax
Step2
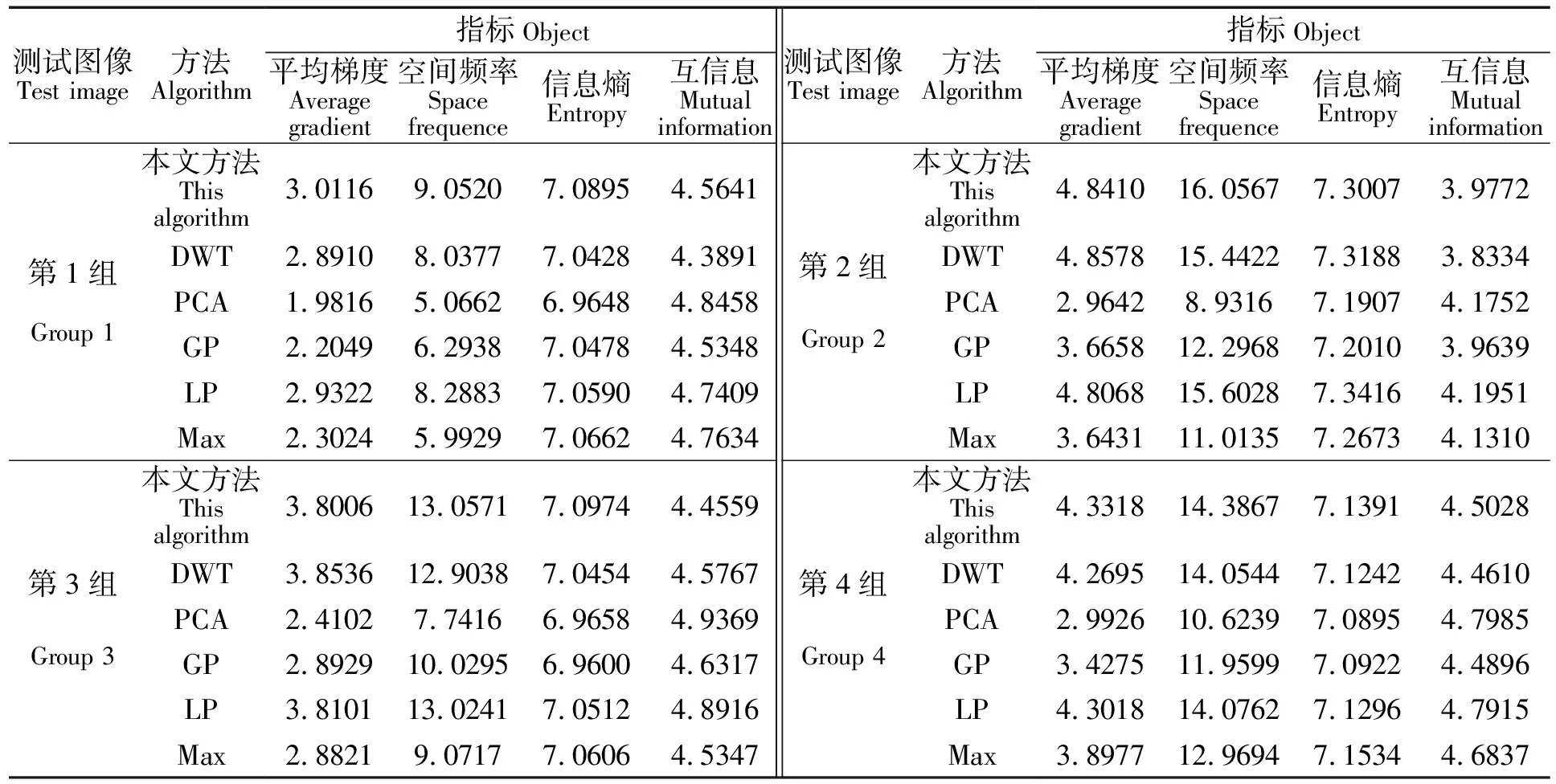
whilei { fork=1 to 2 { 计算r=I0-I1-I2; 对Ik+r做变换Tk,得系数α1; } δ=δ-(λmax-λmin)/N; i=i+1; } 迭代结束完毕,即可获得低频分量I1和高频分量I2,且I0≈I1+I2 如图2所示,a、b分别为原始的左聚焦和右聚焦图像,c、e分别为a经分解后得到的低频分量和高频分量,d、f分别为b经分解后得到的低频分量和高频分量。 由于分解后的低频系数保留了大量的原始图像整体特征的信息和部分边缘信息,因此在融合过程中需要选取较为清晰的部分。由于图像中清晰的部分往往体现出较高的对比度,每个像素点与其相邻的像素点的差值相对较大,即图像清晰程度由区域内像素共同决定。因此在光滑部分的融合中需要充分体现其细节信息,细节信息越丰富的部分,图像就越清晰。Jiang等[27]认为图像分解后的系数的绝对值体现了细节信息的保留程度,因此建议分解后采用绝对值最大法进行融合。为了能进一步评价低频分量中的点特征活跃度,本文使用高斯差分模板[28]作为低频点特征活跃度的算子,由此来定义低频系数的融合规则。 故高斯差分算子F定义为: (4) 由于高斯模板滤波是对图像进行平滑处理,两个高斯模板滤波后相减即把图像中灰度值变换比较平坦的区域给消除掉了,故高斯差分模板可以作为边缘检测和特征提取的算子[29-30]。本文对低频分量使用高斯差分算子作为细节特征活跃度的衡量标准。 定义2 特征活跃度fa(x,y)=F*f(x,y),在融合过程中,fa(·)的值越大,代表该点能够体现的细节信息和特征越多,表明该像素点与其邻域的对比越大,即表明该点的清晰度越大,因此低频分量的融合规则为: LF(i,j)=αij×LA(i,j)+(1-αij)×LB(i,j), (5) 其中αij=faA(i,j)/(faA(i,j)+faB(i,j))。 由于高频分量是在原图像中去除了低频信息,其主要保留的是图像中的细节信息,因此在融合过程中需要选取较为清晰的部分。由于图像的每一个像素点与其相邻的像素点都是相关的,图像清晰与否由区域内像素共同决定,因此在决定高频分量融合时,需要充分考虑与其相邻像素的关系。为了体现像素点的清晰度,本文在纹理部分采用加权边缘信息用于判断像素点的清晰度。本文定义细节信息(details information)作为高频分量融合的标准。 定义3 细节信息 (6) 其中,细节信息窗口大小为(2s+1)×(2t+1)。 本算法的高频信息的融合规则为 (7) 为了对上述算法进行验证,本文使用了图3的四组测试图像进行实验仿真,采用Matlab R2015b进行仿真实验,分解迭代次数为60次。同时对基于离散小波变换的融合算法(记为DWT)、基于PCA的融合算法(记为PCA)、基于金字塔的融合算法(梯度金字塔(记为GP)和拉普拉斯金字塔(记为LP))和使用系数的绝对值最大法的融合算法(记为Max)等五种算法进行了仿真实验。实验结果如图4所示。 图4显示了六种图像融合的算法,可以看到,本文方法的融合算法与绝对值最大法、基于DWT、基于PCA、梯度金字塔和拉普拉斯金字塔方法的融合算法在视觉效果上看差不多。 为能进一步说明本算法,本文同时进行客观评价指标的评价。客观评价指标有: 1)平均梯度 (8) 其中,Gx(i,j)和Gy(i,j)分别为像素点(i,j)在x方向和y方向的一阶差分。 2)空间频率 (9) 其中,FR和FC分别表示图像的行频率和列频率, 3)熵 (10) 4)互信息 MIAB/F=MIAF+MIBF, (11) 其中 pAF(i,k)与pBF(i,k) ,i,k=0,1,…,L-1分别表示源图像A与融合后图像F的联合直方图和源图像B与融合后图像F的联合直方图。 从表1可见:从平均梯度上看,本文所提出的算法在实验数据上比大多数的融合算法都要好,仅仅在第2组中稍弱于DWT方法;从空间频率上看,本文提出的图像融合算法均比传统的融合算法来得更好;在信息熵方面,本算法在第1组和第3组中也表现出比其他融合效果更好的指标,在第2组中仅稍弱于DWT方法与拉普拉斯金字塔方法,在第4组中仅稍弱于系数绝对值最大法。说明该方法在从源图像获取梯度信息、边缘保护等方面要优于其他算法。但本文的方法也存在一定的不足,那就是在互信息的指标上显得相对较弱。 表1 测试图像的客观评价指标 本文根据稀疏表示的特点,使用迭代分解的方法,提取图像的不同形态分量。在低频分量,本文使用高斯差分算子来定义图像的特征活跃度,并以此作为融合规则;而在高频分量中使用加权模板定义细节信息,并相应作为融合规则。最后将融合后的低频分量和高频分量叠加得到最终的融合图像。实验结果表明,该方法在主观评价中有着较好表现,同时,在客观评价中大多数指标优于其他图像融合算法。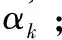
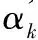
2.3 低频系数融合规则
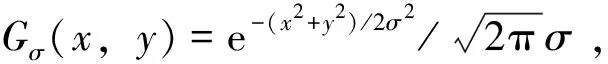
2.4 高频系数融合规则
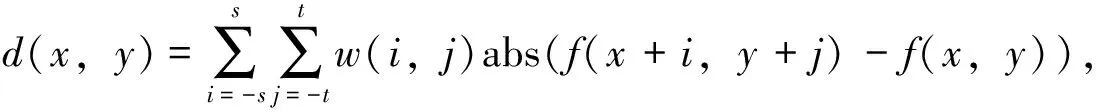
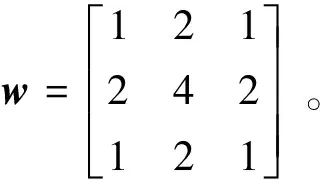
3 实验结果与分析


4 结论
