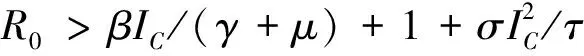一类具有媒体报道的传染病模型

陈 娟，戴斌祥，李文秀

(1.集美大学理学院，福建 厦门361021；2.中南大学数学与统计学院，湖南 长沙 410083；3.湖南大学数学与计量经济学院，湖南 长沙 410082)

0 引言

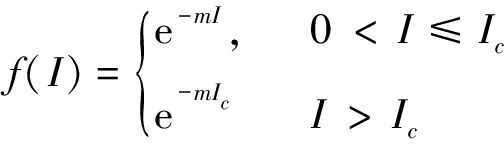
(1)

然而，媒体报道与传染率不单呈指数递减趋势，媒体报道量与染病者的数量以及前期媒体报道的多少有关。文献[9]引入了媒体报道量随着时间变化的函数M(t)，建立了一个非线性传染病模型并进行了理论分析。

本文将媒体报道量M视为时间t的函数，利用分段连续函数β/(1+εMI)来刻画媒体报道对感染率的影响，其中ε如式(1)所定义，建立了一个与媒体报道有关且具有分段感染率的传染病模型，并对其进行动力学分析，以此来研究媒体报道对传染病模型的影响。

1 模型的建立

首先将人群划分为易感者S(t)和感染者I(t)，M(t)表示t时刻的媒体报道量，用β/(1+εMI)来表示媒体报道对疾病传染病的消减作用，则可得到如下的传染病模型：

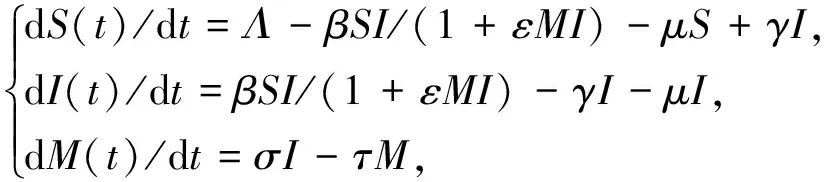
(2)

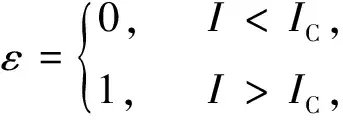
系统(2)是分段光滑系统，可将其分为两个系统，令H(Z)=I-IC，其中Z=(S,I)T，当H(Z)<0时得到的系统称为FG1；当H(Z)>0时得到的系统为FG2。故系统(2)可写成如下的分段光滑系统：

(3)

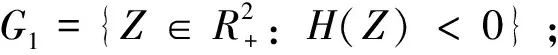
定义1 对于分段光滑系统(3)，若点Z*满足FG1(Z*)=0，H(Z*)<0或者FG2(Z*)=0，H(Z*)>0，那么称点Z*为系统(3)的真平衡态；如果点Z*满足FG1(Z*)=0，H(Z*)>0或者FG2(Z*)=0，H(Z*)<0，那么称点Z*为系统(3)的假平衡态。

2 模型的分析

对于系统FG1和FG2，解得其无病平衡点均为E0=(Λ/μ,0，0)，基本再生数均为R0=Λβ/(μ(γ+μ))。当R0>1时，系统FG1的正平衡点为：E1=((γ+μ)/β,(Λβ-μ(γ+μ))/(βμ),σ(Λβ-μ(γ+μ))/(τβμ))；系统FG2的正平衡点E2满足：

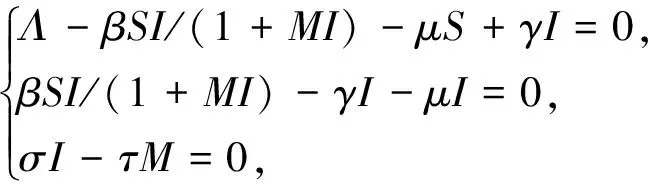
(4)

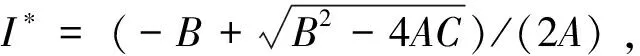
计算出平衡点之后，根据感染者数目I和临界值IC的关系，以下分两种情况讨论。

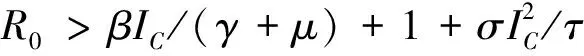
2)在IβIC/(γ+μ)+1时，E1是系统FG1的假平衡态；当1

定理1 对于子系统FG1，当R0<1时，无病平衡点E0是局部渐近稳定的；当R0>1时，正平衡点E1是局部渐近稳定的。

当R0<1时，βΛ/μ-γ-μ=[βΛ-μ(μ+γ)]/μ<0，故E0是局部渐近稳定的。

定理2 对于子系统FG2，当R0<1时，无病平衡点E0是局部渐近稳定的；当R0>1时，正平衡点E2是局部渐近稳定的。

证明由定理1和定理2可知，正平衡点E1和E2分别是局部渐近稳定的，由Poincare-Bendixon定理，只需证明系统不存在极限环即可。

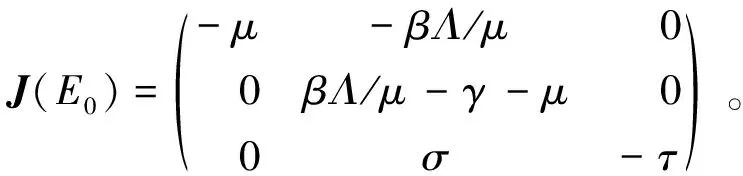
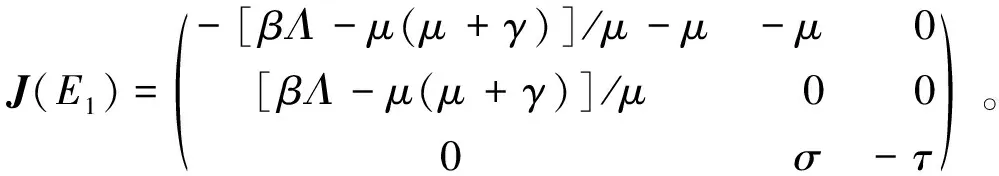
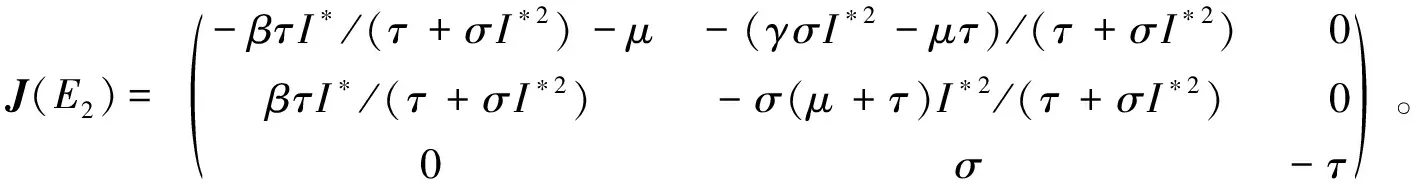
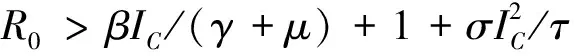
取Dulac函数B=1/(SI)，则有：BF=Λ/(SI)-β/(1+εMI)-(μ/I)+(γ/S)，BG=β/(1+εMI)-(γ/S)-(μ/S)，可得：当IIC时，∂(BF)/∂S+∂(BG)/∂I=-Λ/(S2I)-γ/S2-βM/(1+MI)2<0。故由Dulac准则知系统(2)不存在极限环。 所以，在给定条件下，E1和E2分别是全局渐近稳定的。定理3证毕。

3 结论