四旋翼飞行器有界输出控制
2019-03-14师五喜李康利
师五喜,李康利
(天津工业大学 电气工程与自动化学院,天津 300387)
近年来,四旋翼飞行器由于其结构简单且具有垂直起降、定点悬停、侧飞、倒飞等高机动性的特点而被广泛关注,其中控制器的设计是一个研究热点,各国学者都在设计不同的控制器对四旋翼无人机的位置、姿态进行控制。目前对四旋翼飞行器的控制方法主要有 PID 控制[1]、反步法控制[2-3]、动态面控制[4-5]、滑模控制[6-7]、自抗扰控制[8]等。虽然这些方法有效地实现了四旋翼飞行器的稳定控制,但鲜有考虑其有界输出问题。对四旋翼飞行器来说,其位置、姿态的有界输出控制有助于改善其动态性能,且能够有效保证四旋翼飞行器和操作人员的安全。
目前实现有界输出控制的方法主要有:基于不变集和允许集的控制[9-10]、模型预测控制[11-12]、参考设定法[13]。然而,以上方法要么依赖于数值计算要么所提出的算法相当复杂,很难应用到实际系统中。一些学者应用障碍Lyapunov函数(barrier Lyapunov function,BLF)方法实现了有界输出控制,文献[14]针对一类严格反馈非线性系统,将BLF和反步控制方法相结合来设计控制器来保证输出有界。文献[15]在文献[14]的基础上提出了一种时变BLF,使得输出值的约束是随时间变化的。在文献[16]针对一类含有Bouc-Wen迟滞模型的输出受限非线性系统,将BLF和反步控制方法相结合来设计控制器,解决了系统输出有界问题。文献[17]针对海洋表面船只系统的输出受限问题,利用BLF结合反步法设计控制律,并用神经网络来逼近未知模型参数和干扰项。但是基于BLF函数的非线性系统反步控制中,存在控制器结构复杂、约束量初值选取区间小等问题,针对以上问题文献[18]提出了一种基于非线性映射的自适应反步控制方案,增加了系统初值选取,降低了控制器设计的复杂性。文献[19]提出采用切换控制方法,通过滑模控制将系统约束量控制到BLF的收敛域之内,然后采用BLF和反步法设计控制器,实现输出有界控制。文献[20]针对一类具有未建模动态的非线性系统,提出一种基于BLF和自适应动态面的控制方案,采用动态面的控制方法相较于反步法,降低了控制器设计的复杂性,但是反步法和动态面控制方法需要对控制对象进行精确建模,抗干扰能力较差。由文献[2-7]可知,与反步法和动态面控制方法相比,滑模控制器设计更为简单,具有较强的鲁棒性,抗干扰能力较强。因此本文提出了一种BLF结合滑模变结构的方法设计四旋翼飞行器的控制器,该方法不仅能使系统的实际输出跟踪期望输出,而且能够保持在预先设定的有界区间内,最后通过仿真和实验证明了该方法的有效性。
1 系统建模和问题描述
四旋翼飞行器的简化模型如图1所示。
图1中定义了2个坐标系:机体坐标系{B}和地面坐标系{E},满足右手定则,规定y轴正方向为飞行器飞行的正方向。Fi(i=1,2,3,4)为飞行器4个旋翼产生的升力,旋转方向如图1所示,φ、θ、ψ分别为滚转角、俯仰角和偏航角。
忽略陀螺效应、参数摄动等模型不确定影响及外部干扰,采用牛顿欧拉公式推导,四旋翼飞行器简易的动力学模型为[7]:
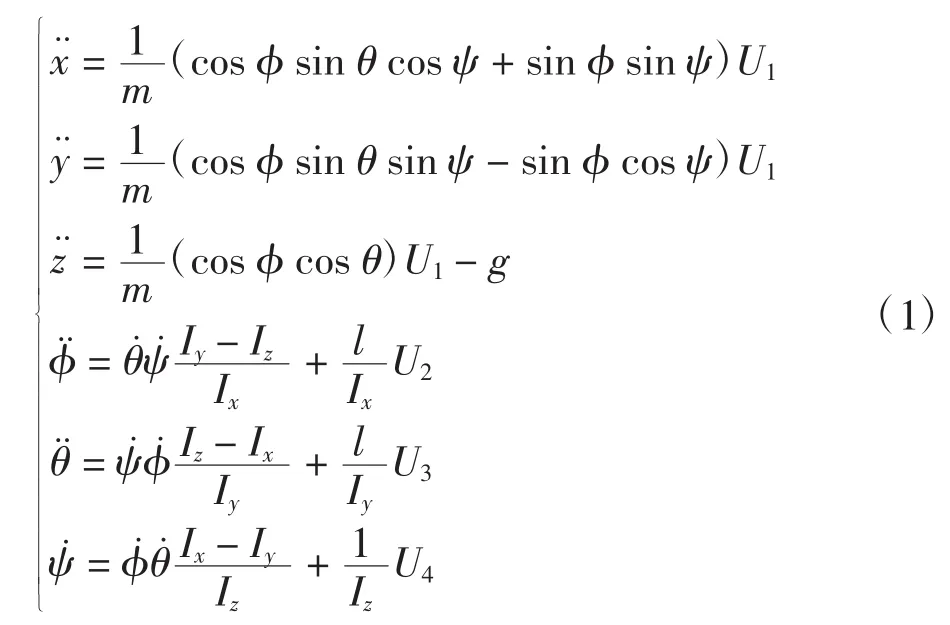
式中:m为四旋翼飞行器质量;φ、θ和ψ分别为滚转角、俯仰角和偏航角;Ix、Iy、Iz分别为关于 x、y、z轴的转动惯量;l为力臂;U1、U2、U3、U4为中间控制输入。

式中:F1、F2、F3、F4分别为4 个电机的升力;τ1、τ2、τ3、τ4分别为4个电机产生的反扭矩。
将式(1)改写为:
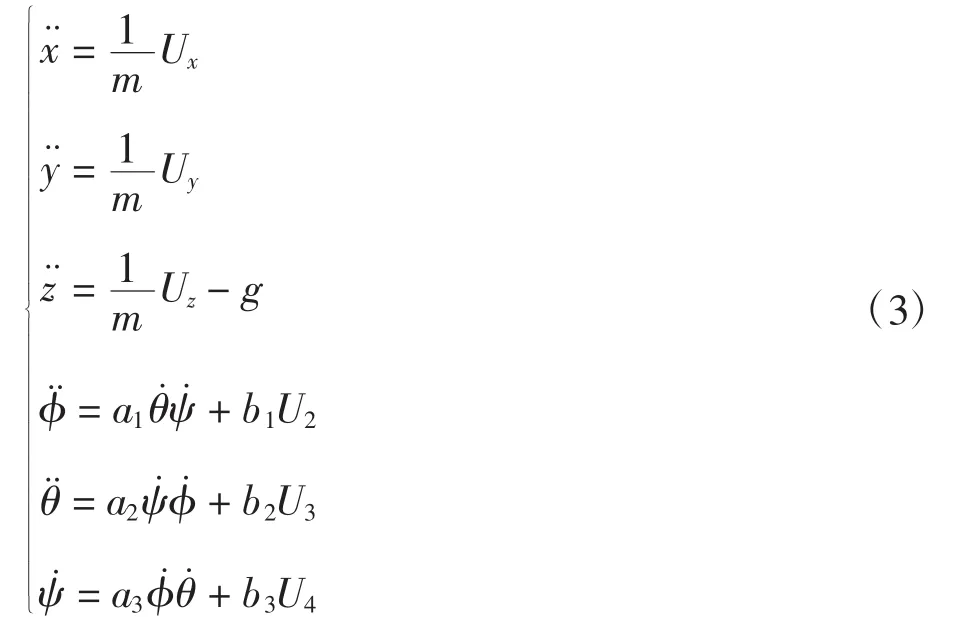
式中:a1=(Iy-Iz)/Ix;a2=(Iz-Ix)/Iy;a3=(Ix-Iy)/Iz;b1=l/Ix;b2=l/Iy;b3=1/Iz;Ux、Uy、Uz为:
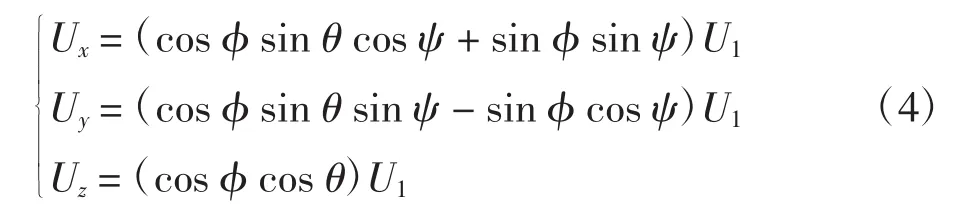
由上式可知,四旋翼飞行器动力学模型6个通道,每一个通道都可以写成如下形式的二阶系统:

式中:x1、x2为状态变量;f(x)∈R为模型已知部分;b为模型已知参数;u∈R为系统的控制输入;y1∈R为系统的输出。
本文的控制目标是设计一种基于BLF和滑模控制的控制器,使得式(5)所描述的四旋翼飞行器系统的输出y1能跟踪期望输出y1d,同时保证闭环系统的所有信号半全局一致终结有界,且满足|y1|<kc的约束条件,其中kc>0,为设定的常值界限。

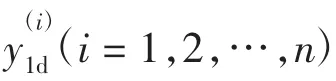
为了保证四旋翼飞行器系统的输出值有界,本文提出以下引理:
引理1:对于任意正常数λθ考虑如下滑模面


成立,则有输出值|y1|< kc,∀t≥0,其中 kc> 0。
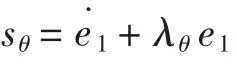

由于|sθ|< λθ(kc-A0),所以
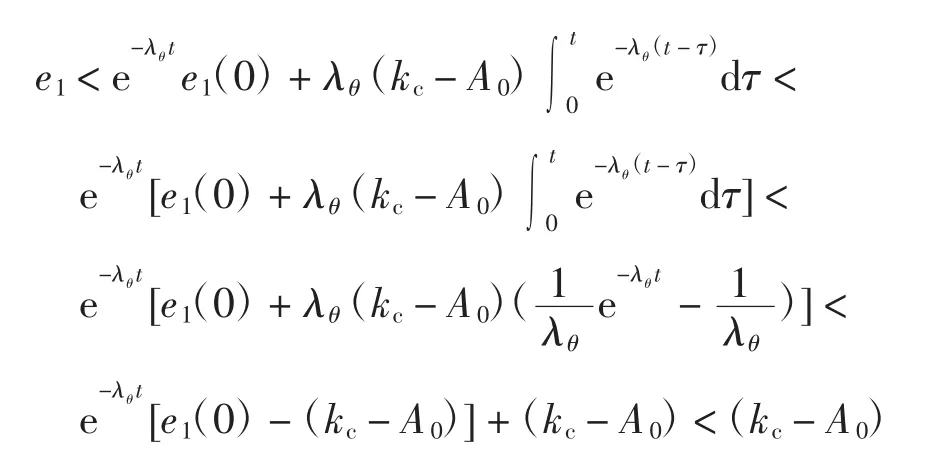
所以
y1<y1d+kc-A0<kc
同理可得
y1>-kc
综上所述,若|sθ|<λθ(kc-A0)且满足|e1(0)|<kc-A0的约束条件时,则有系统的输出值|y1|<kc。
2 障碍Lyapunov函数
由引理1可知,要保证四旋翼飞行器输出值有界,必须先要保证滑模面有界,令 kb= λθ(kc-A0),本文定义了如下的障碍Lyapunov函数(BLF):

引理 2[11]:对于任意正常数 kb,δ:={x1∈R:|δ|< kb}⊂R和N:=Rl×δ⊂Rl+1和为开集,考虑系统

取 η :=[ω,δ]T∈N,h:R+× N→Rl+1在定义域内是关于 t分段连续且满足局部一致Lipschitz条件的。假设存在函数U:=Rl→R+和V1:δ→R+在各自的定义域连续可导且正定,并满足
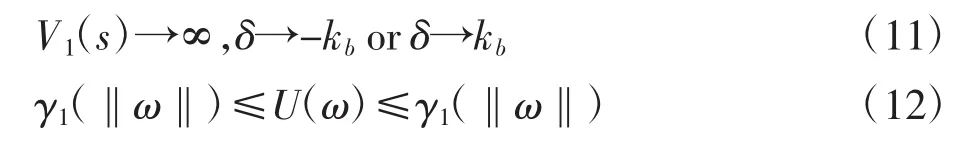
式中:γ1、γ2属于无穷大κ类函数。令V(η):=V1(δ)+U(ω),δ(0)在集合 δ∈(-kb,kb)内,若不等式

成立,则有 δ∈(-kb,kb),∀t∈[0,∞)。
由引理2可知,若采用式(9)所示的障碍Lyapunov函数(BLF),只要满足V˙≤0和|sθ(0)|<kb的条件,就会得到|sθ|< kb,∀t≥0,即|sθ|< λθ(kc-A0)。
3 控制系统设计
3.1 四旋翼飞行器的双闭环控制
根据四旋翼飞行器模型的特点,设计双闭环控制回路,内环为姿态控制,外环为位置控制,如图2所示。
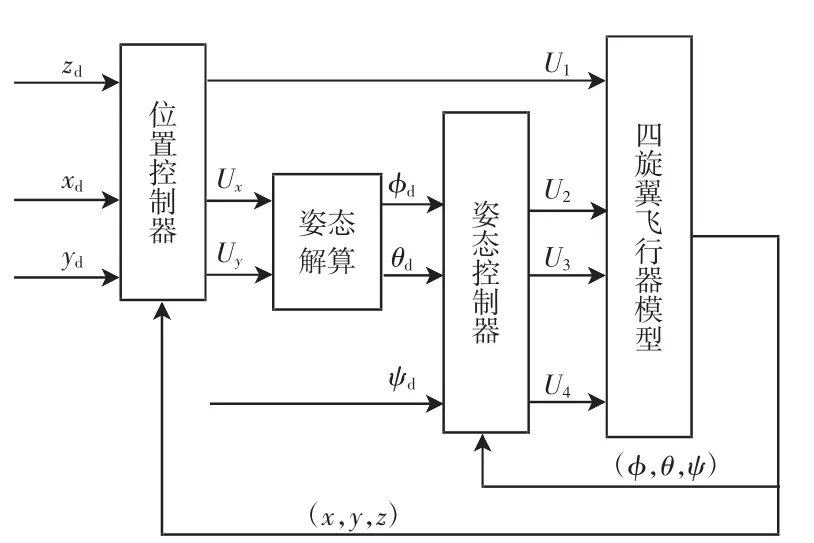
图2 四旋翼飞行器的双闭环控制Fig.2 Double closed loop control of quadrotors
由于四旋翼飞行器姿态和位置之间存在着藕合关系,俯仰角和滚转角的期望值是通过姿态解算模块得到的。
在实际飞行中,由于俯仰角和滚转角都很小,故对其进行小角度假设,即 sin φ≈φ,cos φ≈1,sin θ≈θ,cos θ≈1。
由式(4)可得

反解算得到φd和θd
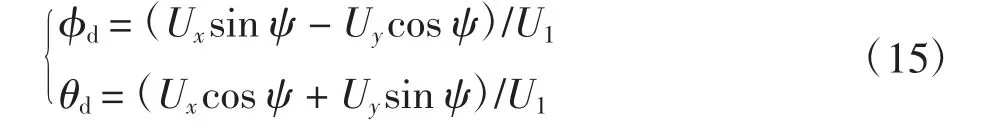
3.2 控制器设计
为了保证所有的输出值有界,本文内外环控制器都采用BLF和滑模相结合的方法设计控制器,下文以俯仰通道为例进行设计。

结合式(5)可得

选取指数趋近律,所以设计如下形式的趋近律

其中k1、k2为正常数。
结合式(16)—(18)设计如下控制律

定理1针对控制对象(5)所描述的四旋翼飞行器系统,若采用(19)式的控制律且满足|eθ|<(kc-A0和|sθ(0)|<kc时,则可使四旋翼飞行器系统的输出y1跟踪期望输出y1d,同时保证|y1|<kc。
证明:定义式(9)所示的障碍Lyapunov函数,并对其求导,将式(17)和式(19)代入可知
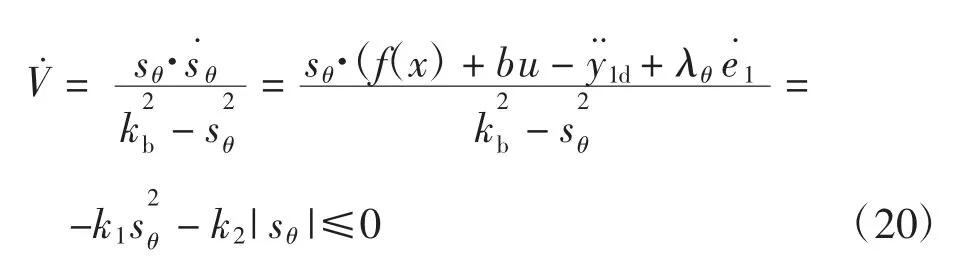
由引理1和引理2可知,定理1成立。
同理可得到其他通道的控制器:
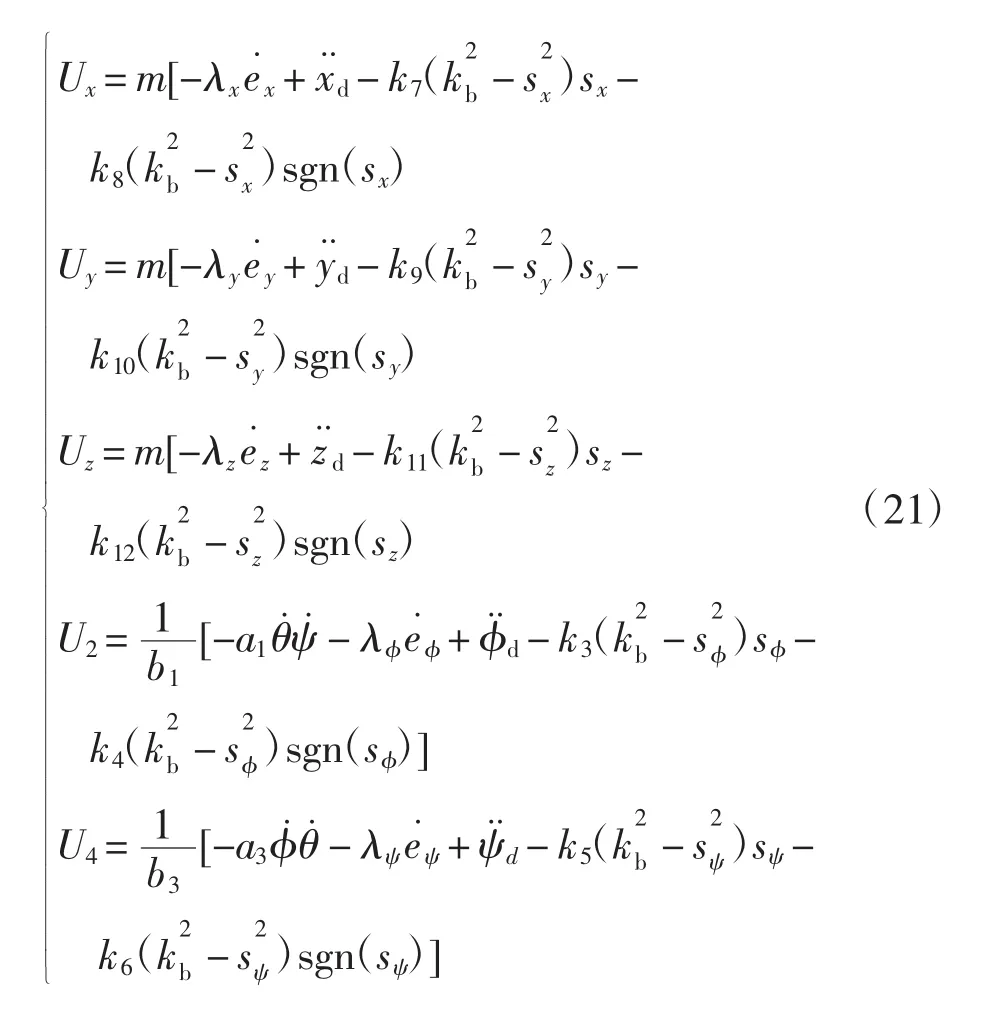
4 仿真和实验
4.1 仿真
本文通过Matlab/Simulink仿真来验证所设计控制器的有效性,将本文所提方法(SMC+BLF)与传统滑模控制方法(SMC)进行了对比仿真,两种情况初始值、期望值和所使用的滑模面相同。
四旋翼飞行器的初始值为
期望值为(xd,yd,zd,ψd)=(0.5,0.5,0.3,0)。
四旋翼飞行器输出值的界限可以根据实际飞行环境进行设定,经过查阅四旋翼飞行器实物飞行实验资料可知,飞行器飞行过程中滚转角和俯仰角在飞行过程中不能超过40°(弧度约为0.698),否则很容易产生飞行事故,因此,本文仿真中位置和姿态的输出界限分别设为kc1=1.1 m,kc2=0.6 rad,以俯仰通道为例,kb=λθ(kc-A0)=0.6λθ,eθ(0)=0,sθ(0)=e˙θ(0)+λe(0)=0,满足|sθ(0)|<kb,|eθ(0)|<kc-A0,的条件,同理易知四旋翼飞行器的所有通道都满足初始条件。
四旋翼飞行器的参数为
m=1.79 kg,g=9.81 m/s2,l=0.2 m,Ix=Iy=0.03 kg·m2,Iz=0.04 kg·m2。
控制器参数选择为:λx=λy=1.41,λz=λθ=λψ=3,ki=0.5(i=1,3,5,7,9,11),kj=5(j=2,4,6,8,10,12)。
仿真结果如图3和图4所示。
由图3和图4可知,四旋翼飞行器在传统滑模控制器的控制下,输出值有较大的超调,都达到或超过所设定的界限,需要较长的时间跟踪上期望值,在本文设计控制器的控制下,相对于传统滑模控制器的控制,输出值全局都在预先设定的界限之内,超调值和跟踪时间都大大减小,输出值在两种控制器的控制下,控制效果非常接近是由于这两个通道与其他通道不存在串级控制、控制模型较为简单而且仿真为理想环境造成的。
4.2 实验
本文利用加拿大Quanser公司开发的四旋翼无人机实验平台进行实验验证,整个Quanser无人机系统的实验环境包括:1架Qball2四旋翼无人机、6个Optitrack摄像头、1台PC主机、内嵌实时控制软件QUARC的Matlab/Simulink和Wifi无线通信,实验环境如图5所示。

图4 姿态环仿真结果Fig.4 Simulation results of attitude loop

图5 实验环境示意图Fig.5 Diagram of experimental environment
由于四旋翼飞行器姿态和位置之间存在着藕合关系,其水平位置的变化,是通过改变姿态角的来实现的,可以说姿态角的控制是实现四旋翼飞行器稳定飞行的前提和基石,本文仅进行了姿态实验验证。
本文以俯仰通道为例,用本文所提方法(SMC+BLF)与传统滑模控制器(SMC)进行角度跟踪对比实验,两种方法采用相同的初始值和期望值,初始值约为0.4°,期望值为10°,设置的界限为21°,易知本实验初始时刻的状态满足初始条件的要求,具体结果如图6和图7所示。其中图6为传统滑模(SMC)控制结果,图7为本文所提方法(SMC+BLF)控制结果。
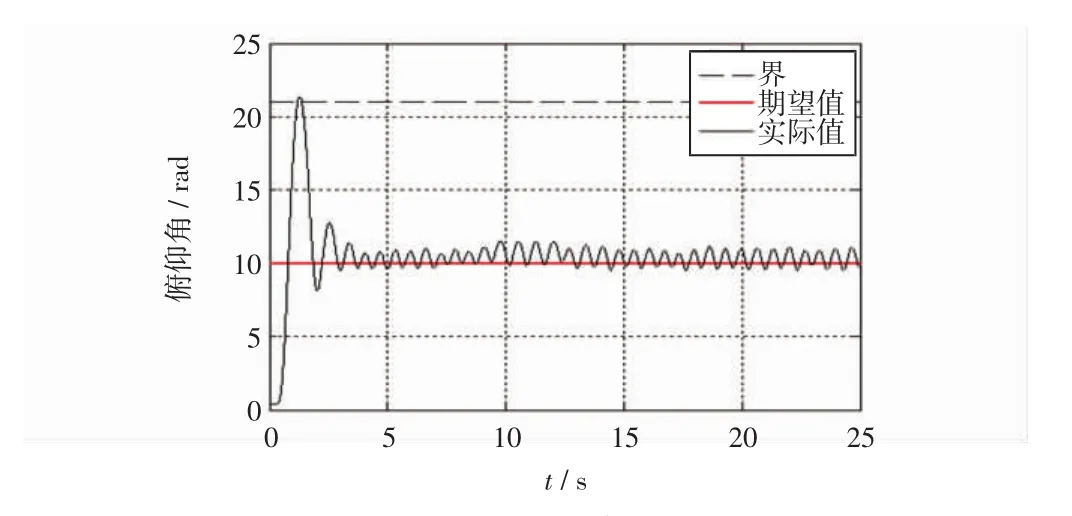
图6 SMC实验结果Fig.6 Experimental results of SMC
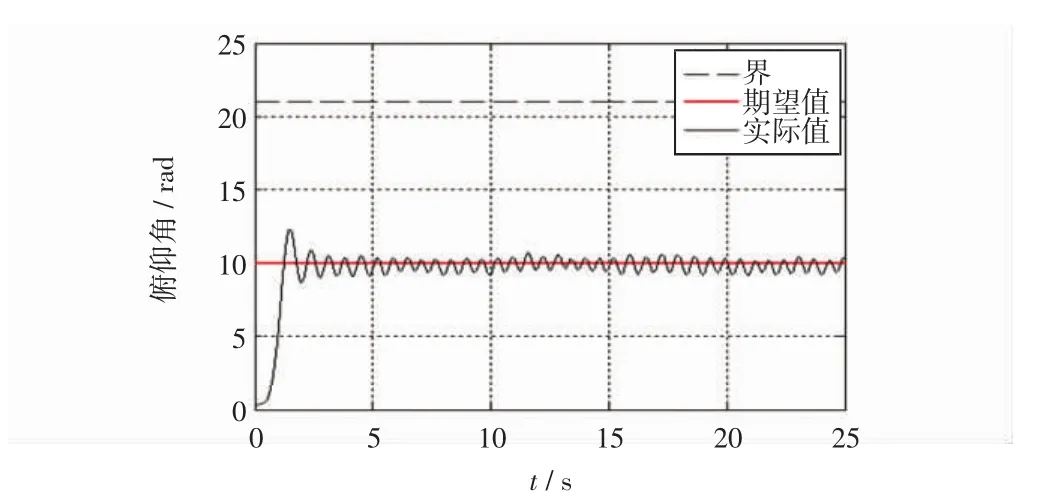
图7 SMC+BLF实验结果Fig.7 Experimental results of SMC+BLF
由图6和图7实验结果可知,两种控制器都能快速跟踪上期望值,然而传统滑模控制器的输出值超过了预先设定的界限,本文控制器的输出值则没有,从而验证了本文方法的有效性。
5 结论
本文针对四旋翼飞行器实际起飞时超调过大问题,提出了一种基于BLF的有界输出控制方法,该方法利用障碍Lyapunov函数将传统滑模面约束在一定的范围内,从而使输出值始终保持在安全的范围内。通过与传统滑模方法的仿真和实验对比研究发现:
(1)传统滑模方法能使系统的实际输出能跟踪期望输出,但是实际输出的超调较大,超出了安全范围。
(2)本文所使用的方法不仅能使系统的实际输出能跟踪期望输出,还能够使实际输出值始终保持在预先设定的安全范围内,从而能保证四旋翼飞行器和操作人员的安全。
