香港地区大气加权平均温度建模与研究
2019-03-14王皓赵兴旺
王皓,赵兴旺
(安徽理工大学 测绘学院,安徽 淮南 232000)
0 引 言
GPS技术经过30多年的发展,在很多相关的领域都得到了应用与拓展,其中在气象学领域GPS技术就发挥了重要的作用,衍生出了地基GPS气象学[1].地基GPS气象学最核心的原理就是当GPS信号穿过大气到达地面GPS接收机时受到大气中水汽的影响会产生延迟,利用这种延迟与沿信号传播路径上的大气水汽的总含量的正比关系,使用公式将湿延迟转变成大气可降水量(PWV).而这两种物理量之间的转换必须使用到大气加权平均温度,因此为了能够提高反演PWV计算结果的精度,需要建立更加适用于当地的加权平均温度计算模型,来降低或消除加权平均温度计算时的误差,以此推动地基GPS水汽反演技术的进一步发展[2].
如何提高大气加权平均温度计算精度,国内外都进行了大量的研究,Bevis首先分析出地表温度Ts与加权平均温度Tm的线性关系,并提出了适用于中纬度地区的Bevis经验回归公式[3].Ross等[4]通过对全球53个探空站23年的探空数据研究,总结出地理位置与季节的变化对于Tm与Ts的相关关系的影响.李建国等人[5-10]分别利用不同地区的探空资料建立了本地化大气加权平均温度模型.王晓英等[11]利用香港探空站2003-2009年数据建立了香港地区的Tm回归方程,并且分析了Tm回归方程随季节变化的规律.姚宜斌等[12]提出了一种可以直接通过测站三维坐标和年积日来对全球加权平均温度Tm进行计算的新模型GWMT.鉴于加权平均温度的重要性,本文将利用回归分析的方法,对2007-2016年香港探空数据进行建模,并从整体计算结果精度对比、季节影响和昼夜影响三个方面进行分析.
1 香港加权平均温度模型建立
1.1 水汽反演的基本原理
地基GPS气象学中,PWV可以通过GPS信号在天顶方向上的湿延迟(ZWD)进行转换,转换公式为[13]
PWV=∏·ZWD.
(1)
其中无量纲水汽转换系数∏为
(2)
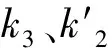
(3)
Tm是局地气柱中考虑了水汽压权重的垂直积分平均温度.因为e和T的数值会随着时空的改变而改变,所以式(3)得出的Tm也具有时空变化特性.
由公式(2)以及公式(1)可以得出Tm的精度决定了转换系数∏的精度,进一步影响着水汽反演得到最终结果PWV的精度.
1.2 加权平均温度模型的建立
因为香港探空站(站号45004)数据充足,获取方便,层数较多,所以本文利用香港京士柏探空站2007—2017年逐日数据进行数据分析,通过MATLAB计算出2007—2017年的加权平均温度Tm.在水汽反演过程中,加权平均温度至关重要,然而,加权平均温度Tm与地面温度Ts,露点温度Td,湿度Es以及水汽压Ps的相关性关系决定了我们加权平均温度回归模型建立的方式,并最终影响着水汽反演的精度,故先分析Tm-Ts、Td、Es、Ps线性关系,如图1和表1所示.
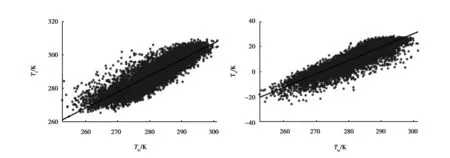
(a)Tm-Ts线性关系图 (b)Tm-Td线性关系图
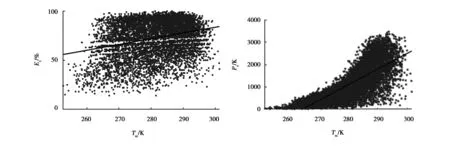
(c)Tm-Es线性关系图 (b)Tm-Ps线性关系图图1 Tm-Ts、Td、Es、Ps线性关系图

因素Tm-TsTm-TdTm-EsTm-Ps 相关系数0.890 10.895 20.281 30.772 4
由图1和表1可以得出Tm与Ts、Td、Es、Ps都具有非常高的相关性,并具有良好的线性关系,在此基础上,统计分析并建立香港地区的本地加权平均温度计算模型,具体结果如表2所示.
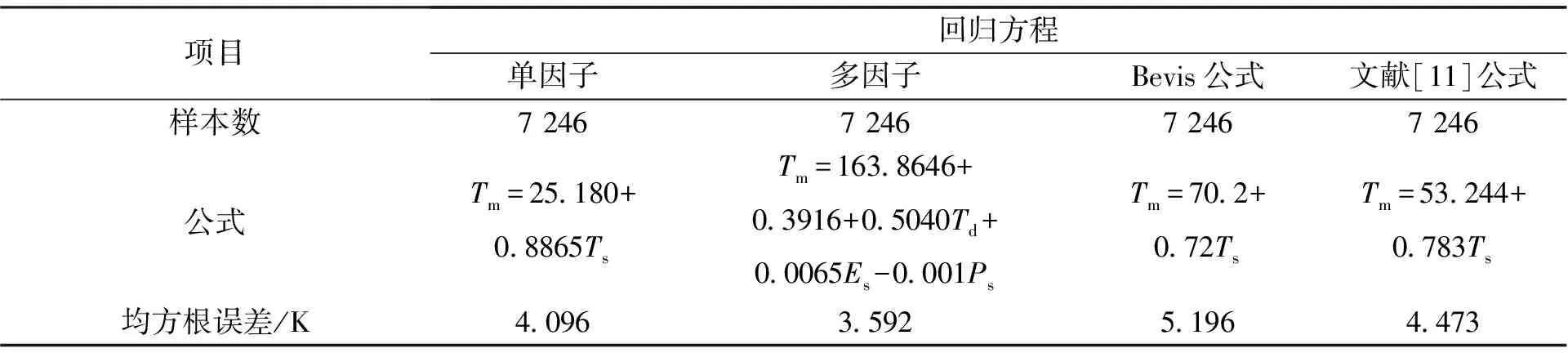
表2 香港地区2007—2016年探空数据回归分析结果
文中利用多年的探空数据反演出了单因子以及多因子的回归方程,并且通过均方根误差可以看出,单因子和多因子回归方程的计算结果经度要远高于Bevis公式以及文献[11]公式.
2 实验分析
为了验证本文模型的适用性,将两种模型2017年的Tm预测值在整体精度进行对比、季节影响和昼夜影响三个方面进行分析.
2.1 本地化模型的效果检验
利用前文得到的本地化单因子和多因子计算模型,将香港地区2017年的探空资料代入到计算模型,得到Tm的回归预测值,与真值进行对比分析,得到两种本地化模型、Bevis公式和文献[11]公式的偏差分布直方图,如图2所示.
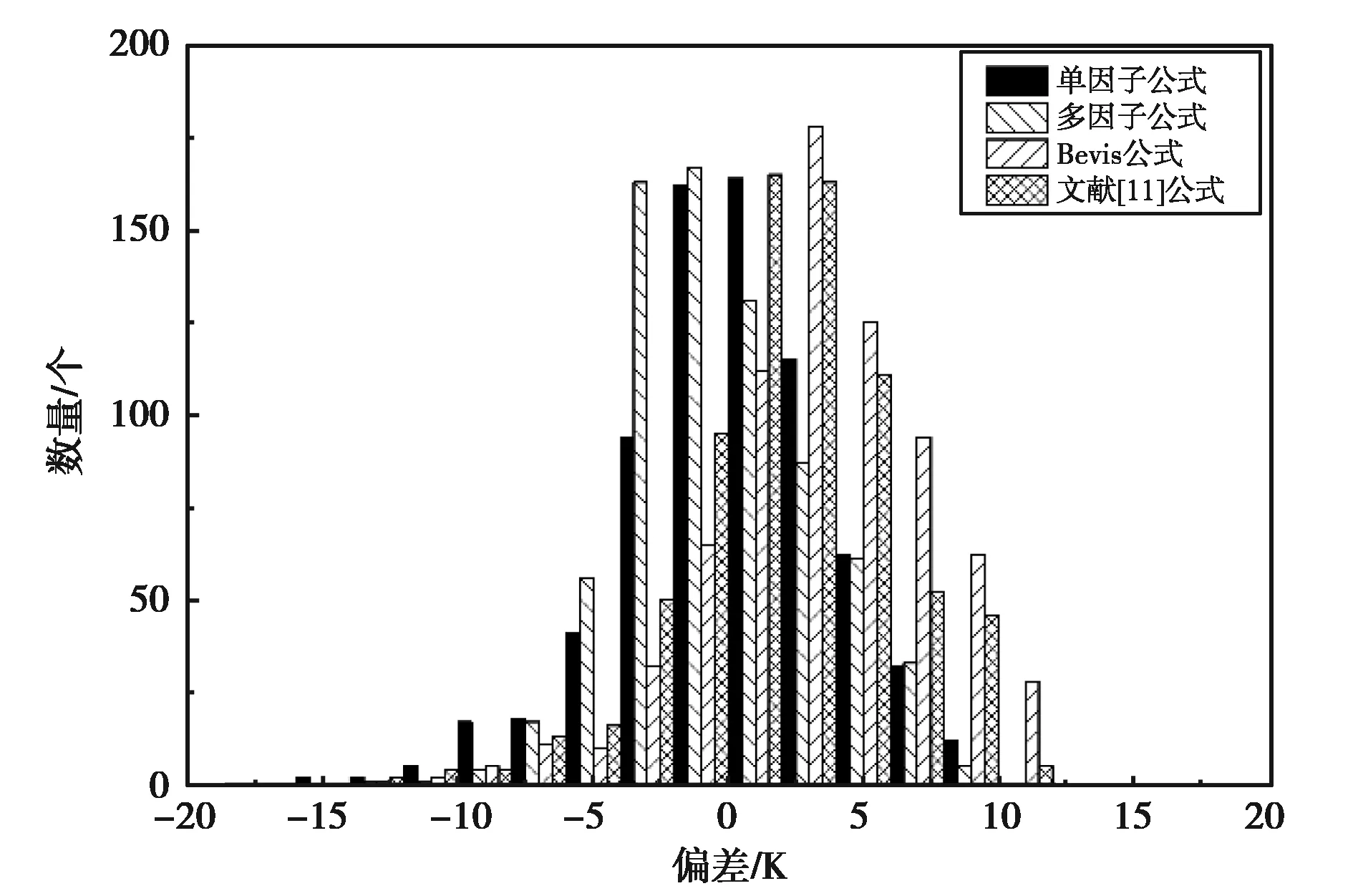
图2 2017年预测值偏差分布图
由图2可知,单因子公式预测值与真值的偏差在—5~5 K的个数所占比例达到80.72%,多因子公式的预测值与真值的偏差在-5~5 K的比例达到85.26%,Bevis公式的预测值与真值的偏差在—5~5 K的比例为64.05%,5~10 K的比例为28.37%,文献[11]公式预测的结果与真值的偏差在—5~5 K的比例达到73.97%,5~10 K的比例为20.39%.由此可见本文得到的单因子及多因子公式的预测结果均优于Bevis公式和文献[11]公式得到的预测结果,并且多因子公式精度更高.
为了对本文得到的两种本地化模型的精度进行进一步的检验,将单因子以及多因子模型得到的2017年Tm预测值与Bevis经验公式和文献[11]公式得到的估计值以及探空计算得出的真值在绝对误差、均方根误差和相对绝对误差等方面进行对比,得到表3所示的结果.
表3中的计算结果表明,两种本地化计算模型算出的Tm与Bevis公式以及文献[11]公式估算的结果相比,绝对误差、均方根偏差以及相对绝对误差都得到了明显的减小,本地化模型预测的结果与真值明显更加接近,计算结果的精度得到显著的提高.
在单因子与多因子模型预测结果进行比较时,两者之间的绝对误差差值为0.015 9 K,均方差差值为0.385 6 K,相对绝对误差差值为0.02 K,由此可以得出虽然多因子模型的精度更高,但提高得并不明显,因此在对精度要求不高的水汽反演计算中完全可以使用单因子模型代替多因子模型.

表3 单因子和多因子本地化方程、Bevis公式、文献[11]公式与真值的对比检验
2.2 Tm回归模型季节影响统计分析
为了分析Tm回归方程与季节变化之间的关系,将香港京士柏探空站2007—2016年的数据按春夏秋冬进行分类,并按季节建立春夏秋冬的Tm回归方程,并预测2017年的结果,如表4所示.

表4 分季节回归方程统计结果
从表4中可以看出春夏秋三个季节反演出的回归方程的a,b值非常接近,冬季的方程与其他三个季节的差距较大;同时未分季节的方程拟合出来的结果与真值的均方根误差与分季节的拟合结果差距并不大,甚至在春夏秋三季中,使用单因子方程拟合的结果要好过于分季节方程的结果,因此可使用单因子回归方程来代替分季节回归方程.
2.3 Tm回归模型时间影响统计分析
在使用探空气球探测高空气象数据时,由于技术、资金等原因,一天只探测了世界时0:00和12:00两次的实时数据.为研究昼夜变化对加权平均温度的影响,本文利用2007—2016年的探空数据分别建立0:00和12:00的回归方程,并预测2017年的结果,如表5所示.

表5 分日夜方程统计结果
从表5可以看出按0:00、12:00分别建立的回归方程拟合出的结果与真值的均方根误差与未分时间拟合的结果之差甚至大于2 K,所以在最后解算大气可降水量时,如果对结果精度要求较高时,还是需要按0:00、12:00分别建立回归方程.
3 结束语
通过香港京士柏探空站2007—2017年探空数据分析与研究,得到以下的结论:
1)Tm与地面温度,露点温度,水汽压以及湿度都具有较好的线性关系,加权温度与地面温度,露点温度和湿度呈现出正相关,与水汽压呈现出负相关.
2)单因子和多因子模型计算结果与真值的偏差在-5~5 K分别占比80.72%和85.26%,远远高于Bevis公式的64.05%和文献[11]公式的73.97%,并且单因子与多因子模型预测结果的绝对误差差值为0.015 9 K,均方差差值为0.385 6 K,相对绝对误差差值为0.02 K,可以得出本文得到的单因子及多因子公式的预测结果均优于Bevis公式和文献[11]公式,但单因子和多因子模型在计算PWV时不会造成显著差异.因此在一般的计算中完全可以使用单因子模型代替多因子模型.
3)按季节线性回归的方程拟合出的结果与全年方程拟合的结果差异值小于0.1 K,由此可见季节方程拟合结果与全年方程拟合结果具有一致性,可用全年方程代替季节方程进行计算.按0:00、12:00分别建立回归方程拟合出的结果与全年方程拟合的结果差异值均大于1 K, 0:00的差异值甚至大于2 K,因此为了提高最终解算PWV精度还需对0:00、12:00分别建模.
在水汽反演的计算中,利用长期气象资料建立适用于当地的加权平均温度计算模型,能够有效提高GPS反演大气水汽计算结果的精度,并对地基GPS气象学的发展具有重要意义.
