基于网络效用最大化理论的分布式车联网拥塞控制策略

谭国真，韩国栋，张福新，丁男，刘明剑

（1. 大连理工大学计算机与科学技术学院，辽宁 大连 116024；2. 山东科技大学计算机科学与工程学院，山东 青岛 266590；3. 大连海洋大学信息工程学院，辽宁 大连 116023）

1 引言

协同车辆安全性系统（CVSS, cooperative vehicle safety system）[1]作为车联网中最具挑战性的车辆安全应用之一，依赖周期性广播的单跳数据分组来追踪周围车辆。数据分组中包含车辆的基本状态信息（如速度、加速度、位置等信息），CVSS依赖这些数据分组追踪邻居车辆的位置，从而避免车辆之间的碰撞[2]。由 IEEE设计的 802.11p协议和1609.x协议组成的WAVE通信架构专门用于车联网通信，被美国和欧洲所采用[3]。基于这些协议，CVSS能够通过车车通信探测到潜在的危险，并且通过及时告警避免车辆之间的碰撞。协同车辆安全系统在车联网安全应用中发挥着重要作用，据统计，该系统可以减少一个国家75%的交通事故[4]。

能否精确地追踪车辆的位置决定了CVSS的性能。本文用追踪精度来表示车辆的真实位置和通过数据分组信息计算得到的上一次车辆的位置之间的误差[5]。当数据分组的数量超过信道最大负载时，数据分组间的碰撞将会增加，从而导致数据分组的接受率下降[6]。由于车辆追踪依赖于周期性广播的数据分组，信道拥塞会严重影响CVSS的追踪性能。为了解决该问题，需要相应的信道拥塞控制策略避免信道拥塞。信道拥塞控制策略主要有3种：1）调节数据分组的发送速率；2）调节传输功率；3）同时调节数据分组发送速率和传输功率[7]。上述的 3种方式都可以将信道负载降到最大信道负载（MBL,maximum beaconing load）以下。由于CVSS中的每辆车依赖周期性数据分组追踪邻居车辆，因此必须满足信道资源分配的公平性，公平性确保每辆车均可以获取有限的信道资源与周围车辆进行有效通信[8]。传统的信道拥塞控制策略[9-15]致力于为每辆车分配相同的信道资源，并没有考虑单个车辆在不同交通场景下的服务需求，因此无法做到信道资源的按需分配。文献[16-17]在信道拥塞控制中考虑了车辆的安全需求，但是所提出的安全权重无法准确描述车辆的安全需求，同样无法做到信道资源的按需分配，且在真实的交通场景下，每辆车的安全需求并不相同。为了保证CVSS能够精确追踪车辆，应该为危险的交通场景下的车辆分配更多的信道资源，否则由于信道资源分配的不合理，车辆之间可能会因无法及时有效通信而发生碰撞。

为了根据车辆安全需求按需分配信道资源，本文提出了一种基于网络效用最大化理论的分布式信道拥塞控制策略。首先，针对 CVSS提出了VANET下信道资源分配的网络效用最大化模型，并且在该模型中提出了反映车辆安全需求的效用函数；然后基于该模型建立了发送功率固定条件下无线信道资源分配的优化问题，该优化问题以实现所有车辆的效用之和最大化为目标；最后为了求解该优化问题，设计了分布式拥塞控制 UBRCC。UBRCC算法在避免信道拥塞的同时，实现了面向单个车辆安全需求的信道资源分配。本文的工作主要体现在以下3个方面。

1）针对CVSS提出了VANET下无线信道资源分配的网络效用最大化模型，并在该模型中提出了反映车辆安全需求的效用函数。

2）基于该模型建立了发送功率固定条件下无线信道资源分配的优化问题，该优化问题以实现所有车辆的效用之和最大化为目标，即最大化满足所有车辆的安全需求。

3）设计了分布式拥塞控制算法UBRCC，解决了无线信道资源的优化问题，在避免信道拥塞的同时满足车辆的安全需求。

2 信道拥塞策略相关研究

对于传统的信道拥塞控制策略，Torrent-Moren等[9]提出了轻量级信道拥塞控制算法D-FPAV。该算法中优先级高的数据分组会被优先发送，可以有效地避免信道拥塞。但是信道最大负载不能自适应于特定的网络环境，且该算法不能根据车辆的安全需求调整传输功率。Khorakhun等[10]提出了一种基于信道占有率的功率调节算法，每辆车根据所测量到的信道占有率调节其传输功率。如果信道占有率超过了门限值，传输功率会被调低，但是准确测量信道占有率非常困难，如果信道占有率测量不准确，算法的可靠性和性能会受到严重影响。Guan等[11]提出了一种基于反馈的功率调节算法，该算法中每辆车根据其邻居车辆的传输功率来调节自身的传输功率。Bansal等[12]提出了基于线性调节的拥塞控制算法LIMERIC，该算法中，每辆车根据单跳传输范围内邻居车辆的数据分组发送速率对自身的数据分组发送速率进行线性调整。Tielert等[13]提出了拥塞控制算法PULSAR，该算法根据单跳及两跳传输范围内邻居车辆的数据分组发送速率调节其发送速率，从而实现全局公平性。Bansal等[14]提出了基于车辆追踪精度的拥塞控制算法EMBARC，当追踪精度超过门限值时，数据分组发送速率将会被提高，然后再根据LIMERIC算法将信道负载控制在MBL以内。Sepulcre等[15]提出了拥塞控制算法 INTERN，该算法将数据分组发送速率跟传输功率结合起来，首先将传输功率设置为所需的最小值，当信道负载超过门限值时根据LIMERIC算法降低数据分组的发送速率。

上述拥塞控制算法[9-15]主要依赖信道的状态信息调节数据分组发送速率或者传输功率来控制信道拥塞，然而这些算法存在2个缺点：1）只有检测到信道拥塞之后才能够采取措施控制信道拥塞，信道拥塞控制存在一定的滞后性，在信道负载从拥塞状态恢复之前，CVSS追踪车辆的误差可能会很大，导致CVSS的性能受到严重影响；2）这些算法主要关注网络层的性能，没有考虑单个车辆的安全需求，因此信道不拥塞时，无法确保每辆车的安全需求得到满足。

近年来，国内外学者对于控制信道拥塞时考虑车辆的安全需求也进行了一定研究。Zhang等[16]引入车辆安全权重的概念来描述交通场景的危险级别，并设计了拥塞控制算法DNUM，其中，安全权重通过两辆车之间的相对速度和相对位移来计算。该算法基于安全权重还提出了效用函数，通过网络效用最大化理论计算最优数据分组发送速率，但该效用函数没有考虑车辆的驾驶方向, 无法准确描述车辆的安全需求，例如两辆车行驶在不同的车道上，虽然安全权重很大，但实际中的交通场景并不危险，因此无法保证车辆的安全需求得到满足。Joerer[17]建立了交叉口场景下的车辆碰撞概率模型，该模型使用两辆车的位移、速度、加速度等来计算碰撞概率，如果碰撞概率超过某个门限值，数据分组发送速率将会增加。然而两辆车之间的碰撞概率很难被精确计算，且文献[17]中提出的计算方法是否精确有待验证。

针对上述拥塞控制策略存在的问题，本文提出了分布式拥塞控制算法UBRCC。UBRCC算法将单个车辆的安全需求考虑在内，在避免信道拥塞的同时公平地按需分配信道资源。与传统的拥塞控制策略相比，UBRCC算法可以保证在危险的交通场景下车辆与周围邻居车辆之间的有效通信。

3 CVSS下的网络效用最大化模型

3.1 VANET网络效用最大化模型

车联网中，每辆车发送数据分组占用的信道资源被该车传输范围的所有车辆共享。本文使用数据分组的发送速率表示每辆车分配的信道资源，通过调节数据分组的发送速率来控制信道拥塞，将信道负载控制在 MBL以内。文献[18]表明，当信道占有率（CBP,channel busy percentage）达到0.6～0.7时，CVSS的吞吐量最大，网络性能最佳，因此将CBP设置为0.6.

用V表示车辆集合，每辆车v以每秒传输rv个数据分组的发送速率广播数据分组，用n（v）表示车辆v的所有邻居车辆，信道负载为每辆车及其邻居车辆的数据分组发送速率之和，通过将该值控制在Cmax（MBL）之下来避免信道拥塞。

车联网下的网络效用最大化问题可以用式（1）来表示。

约束条件为

其中，Uv（rv）表示车辆v的效用函数。式（1）代表每辆车的效用函数之和的最大值。为了实现比例公平性，单个车辆的效用函数如式（4）所示[19]。

其中，权重wv表示车辆v的安全需求，式（2）将信道负载限制在Cmax（MBL）以下，式（3）将数据分组的发送速率限制在之间。通过求解式（1）满足最大值时的数据分组发送速率，实现按照车辆的安全需求公平地按需分配信道资源。

3.2 车辆安全需求

为了表示安全权重wv，需要计算两辆车之间的预计碰撞时间，本文考虑车辆在3种交通场景下的碰撞时间[20]，这3种交通场景分别是车辆跟随场景、车辆相向场景和交叉口场景，基本包含了现实中所有可能的交通场景。针对这3种场景分别给出了车辆可能发生碰撞的条件以及预计发生碰撞的时间。

1）车辆跟随场景

该场景下两辆车A和B相互跟随，如图1所示。Aθ和Bθ分别为车A与车B的驾驶角度，δ表示车A与车B驾驶角度差值的绝对值，当δ足够小时，可以认为θA≈θB。通过判断车A与车B是否按照相同方向行驶，两车之间的安全距离为

其中，dmin表示两辆车之间的预计最小可接受距离，tr为人的反应时间，vf、vl为车A和车B的速度，af、al为车A和车B减速时的最大加速度。

图1 车辆跟随场景

2）车辆相向场景

该场景下两辆车A和B驶向对方，如图2所示。θA和θB分别为车A与车B的驾驶角度，通过判断两车是否往相反的方向行驶，当δ足够小时，可以认为车A和车B驶向对方，车A与车B之间的安全距离可以表示为

图2 车辆相向场景

3）交叉口场景

该场景下两辆车A和B通过交叉口，Aθ和Bθ分别为车A与车B的驾驶角度，vA和vB分别为车A和车B的速度，如图3所示，首先通过碰撞预测法[21]判断两辆车A和B的行驶路径是否平行，如果不平行，则两辆车的行驶路径存在交叉点P。通过交叉点P来计算两辆车预计到达交叉点P的时间如式（7）和式（8）所示。

图3 交叉口行驶场景

其中，rn代表向量（xn,yn），函数sign（⋅）用来判断一辆车是否已经驶离交叉点。如果则两辆车A和B预计大约同时到达交叉点，A与B之间将会发生碰撞，其中，λ取决于车的尺寸、速度或者其他因素[21]。A与B之间的安全距离可以表示为

其中，dmin表示两辆车之间的预计最小可接受距离，tr为人的反应时间，vn为车A和车B的速度，an为车A或车B减速时的最大加速度。

对于每辆车v,Cv={c1,c2,c3…} 表示可能与车v发生碰撞的车辆集合。在车辆跟随场景下，对于必须满足以下条件：1）车与车v同方向行驶；2）车与车v行驶路径有重叠；3）车与车v之间的距离小于dsafe_follow；4）vf＞vl，其中，vf为车的速度，vl为v的速度，da为两车间的距离。该场景下车与车v的预计碰撞时间为

在车辆相向行驶场景下，对于∈Cv，必须满足以下条件：1）车与车v反方向行驶；2）车与车v行驶路径有重叠；3）车与车v之间的距离小于dsafe_opposite。该场景下车与车v的预计碰撞时间为

对于每辆车v，使用车v与车vˆ的最小预计碰撞时间来描述车辆在该交通场景下的安全需求，显然碰撞时间越小，交通场景越危险，车辆的安全需求也就越大。

3.3 效用函数

如3.2节所述，对于每辆车v，存在一个集合Cv表示可能与车v发生碰撞的车。假设集合Cv存在x辆车，用Tvvˆ={Tcol1,Tcol2, … ,Tcolx}表示车v与车vˆ之间的预计碰撞时间，用作为安全权重表示交通环境的危险程度。显然对于每辆车v，wv越大则交通场景越危险。为了保证CVSS能够精确地追踪邻居车辆，如果wv越大则应该分配给车辆v更多的信道资源。根据比例公平性[19]，每辆车的效用函数如式（13）所示。

其中，rv为车辆v的数据发送速率，wv为车辆v的安全权重，V为所有车辆的集合，Cv为可能与车v发生碰撞的车辆集合。

由式（13）可知，对于车辆v来说，显然数据分组发送速率rv越大，Uv（rv）越大。因此根据 CVSS信道资源分配的网络效用最大化模型，得到如式（14）～式（16）所示的优化问题。

式（14）是车辆v与其邻居车辆的效用函数之和的最大值，本文优化的目标是求解每辆车的最优数据分组发送速率，满足所有车辆的效用函数之和最大，从而满足车辆的安全需求，使得每辆车在危险的交通场景下可以有效地与周围邻居车辆进行通信，从而精确地追踪邻居车辆并及时发起碰撞预警，确保CVSS的性能。式（15）中的Cmax表示车辆v与其传输范围内邻居车辆的数据分组发送速率之和，用Cmax表示当前的信道负载，rv′为每辆车的数据分组发送速率，n（v）为车辆v传输范围内的邻居车辆的集合。式（15）作为约束条件，将任意车辆v所处无线网络的信道负载限制在Cmax之下，从而避免信道拥塞。为了避免车辆间的数据分组发送速率相差太大，式（16）作为约束条件将数据分组的发送速率限制在之间。

4 分布式拥塞控制算法UBRCC

本节介绍基于效用函数最大化理论避免信道拥塞的UBRCC算法，该算法使用对偶分解来求解方程式（14）中的效用函数最大化问题，为了消除式（15）和式（16）中的约束，首先构造如式（17）所示的拉格朗日方程。

其中，λv是用于消除约束的拉格朗日乘子，可以被看作车v占用信道资源支付的拥塞“价格”。在车联网中，该拥塞“价格”反映了信道的拥塞状态，如果车辆v所处网络的信道负载超过Cmax，则拥塞“价格”vλ增大，反之拥塞“价格”减小。给定一组非负价格，最优的信道资源分配可以表示为

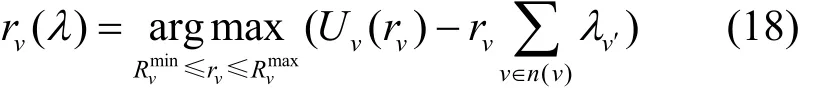
从式（18）可以看出，对于每辆车v，为了计算其最优数据分组发送速率，需要该车的效用函数Uv（rv）以及其邻居车辆的拥塞价格λv′。显然式（17）是带有线性约束的凹函数，根据库恩-塔克条件[22]可知，该方程一定存在最优解，因此一定存在一组最优价格对应式（12）中的最优解。如果能找到最优价格，由式（13）可以根据最优价格求解最优的数据分组发送速率。寻找最优价格的问题可以用如式（19）所示的对偶问题表示。

式（19）被称为对偶方程。由于式（17）是严格的凹函数，所以式（19）也是严格的凹函数，根据库恩-塔克条件存在唯一的一组最优价格。对于唯一的一组最优拥塞价格，存在唯一的一组数据分组发送速率的最优解，此求解最优数据分组发送速率的问题转化为求解最优拥塞价格的问题。

为了计算最优的数据分组发送速率，每辆车需要向其单跳传输范围内的邻居车辆广播拥塞价格。每辆车根据单跳传输范围内邻居车辆的拥塞价格更新数据分组发送速率和拥塞价格。通过梯度下降法反复迭代更新车辆的拥塞价格，直到得到最优的拥塞价格，从而得到最优的数据分组发送速率，如式（20）所示。

基于式（20），本文设计了 UBRCC算法，用来描述拥塞“价格”与数据分组发送速率迭代更新至最优的过程，具体如算法1所示。

算法1UBRCC算法

步骤 1迭代次数k=0：设定每辆车的初始价格为，数据分组的发送速率为。

步骤2第k次迭代：每辆车接收到邻居车辆的拥塞“价格”），然后更新数据分组的发送速率为

其中，算子的分子为车辆v的安全权重，分母为车辆v传输范围内所有邻居车辆的拥塞价格之和。

步骤 3对于第k次迭代：每辆车v更新其拥塞价格为

步骤4反复进行步骤2和步骤3，直到步骤3中拥塞“价格”不再更新时，则得到最优拥塞“价格”，进而根据式（20）得到最优数据分组发送速率，迭代终止。

UBRCC算法中vλ表示车辆v的拥塞“价格”，用来表示信道的拥塞状态，如果当前的信道负载大于信道最大负载Cmax，则拥塞“价格”变大，反之则减小。通过应用梯度下降法反复迭代更新车辆的拥塞“价格”和数据分组发送速率，直到得到最优的拥塞“价格”时，通过式（15）得到最优的数据分组发送速率。wv将数据分组的发送速率与单个车辆的安全权重关联，用来描述交通场景下车辆v的安全需求。选用作为w，即本文只关注车辆vv与v′∈Cv的最小碰撞时间，并用wv表示车辆v所处交通环境的危险级别，wv越大则表示车辆v所处的交通环境越危险。为了保证CVSS能够准确追踪邻居车辆，车v的wv越大则应该分配更多的信道资源。为了避免车辆的数据分组发送速率差别太大，在仿真实验中将车辆的碰撞时间限制为[1,10]之间，因此安全权重wv被严格限制为[0.1,1]之间。参数β用来控制数据分组发送速率的收敛速度。在 UBRCC算法中，β必须被设置得足够小，否则可能导致拥塞价格λ为负值；如果β过大则会导致数据分组发送速率发生振荡。β的界限值在文献[23]中进行了指定。

5 实验仿真与性能分析

5.1 实验条件设定

本节通过在 NS3[24]中进行仿真实验以验证UBRCC算法的性能。在仿真实验中，车辆的速度每2 s变化一次，所以两辆车之间可能会发生碰撞。

在仿真实验中，车辆均匀分布在500 m长的四车道公路上。如图4所示，初始车辆数为100辆，在第20 s时车辆数由100辆增加到200辆，即车辆密度由0.2辆/m增加到0.4辆/m。每辆车使用80 dBm（传输距离为 500 m）的恒定传输功率发送数据分组，所以每辆车都在彼此的传输范围之内。最大信道负载设置为3 Mbit/s，数据分组的大小为512 B，所以信道最大负载可以表示为Cmax=732数据分组/s。仿真参数的设置和算法参数的设置分别如表 1和表2所示。

图4 车辆密度的变化

5.2 实验结果及分析

本节通过对比UBRCC算法与DNUM算法的实验结果以验证算法的性能。DNUM算法首先通过车辆的相对位置xi,j和相对速度vi,j计算出安全权重w，如式（23）所示。

表1 仿真参数

表2 算法参数

然后基于该安全权重通过网络效用最大化理论计算出最优的数据分组发送速率。

1）信道占有率

信道占有率的收敛过程如图5所示，2种算法均可以有效控制信道拥塞。在仿真初期由于数据分组发送速率较低，因此信道占有率也较低。在算法的调节下，数据分组的发送速率增大，信道占有率逐渐保持在0.6左右，信道资源得到充分利用。在第20 s时，由于车辆密度由0.2辆/m增大到0.4辆/m，信道占有率迅速增长，在算法的调节下数据分组的发送速率降低，信道占有率逐渐降低到0.6左右。从图5可以看出，UBRCC算法的稳定性优于DNUM算法，且信道占有率略高于 DNUM 算法，因而信道资源能够得到更充分的利用。

图5 信道占有率的收敛过程

2）追踪精度

本文通过所有车辆追踪其邻居车辆的平均追踪精度来衡量安全应用的性能。2种算法下的跟踪精度如图6所示。从图6可以看出，从0 s到20 s，车辆密度为0.1辆/m，UBRCC算法与DNUM算法均可以将追踪误差保持在0.25 m以下，可以满足安全应用的需求。第20 s时，车辆密度由0.1辆/m增加到0.2辆/m，DNUM算法的追踪误差迅速变大至1 m以上，安全应用的性能受到严重影响；而UBRCC算法始终将追踪误差保持在0.25 m左右。另外，DNUM算法中的安全权重没有考虑车辆的行驶方向，无法准确描述车辆的安全需求，因而无法保证信道资源按照车辆的安全需求公平分配；而UBRCC算法中的安全权重充分考虑了车辆的行驶方向；安全距离等因素，能够更加准确描述车辆的安全需求，因而可以实现信道资源的按需分配，满足车辆的安全需求。

图6 2种算法下的平均追踪精度

3）数据分组递送率

从图7可以看出在仿真初期，由于车辆密度不是很大，2种算法下的数据分组递送率均保持在90%以上。在第20 s时，由于车辆密度的增加，数据分组的递送率开始下降。对于 DNUM 算法，数据分组递送率降至90%之下，无法保证数据分组的可靠传输，安全应用的性能受到影响。而本文的UBRCC算法始终将数据分组递送率保持在90%之上，能够保证数据分组的可靠发送，确保车辆能够将状态信息实时广播给邻居车辆，从而满足车辆的安全需求。

图7 2种算法下的数据分组递送率

4）消息传输时延

从图8可以看出，在仿真初期由于车辆密度不是很大，2种算法下的消息传输时延均保持在25 ms以下，从而满足安全应用的需求。在第20 s时，由于车辆密度变大，消息传输时延随之增加。与DNUM算法相比，UBRCC算法始终将消息传输时延保持在30 ms以下，从而保证车辆及时接收到邻居车辆的数据分组，确保车辆安全应用的性能不受影响。

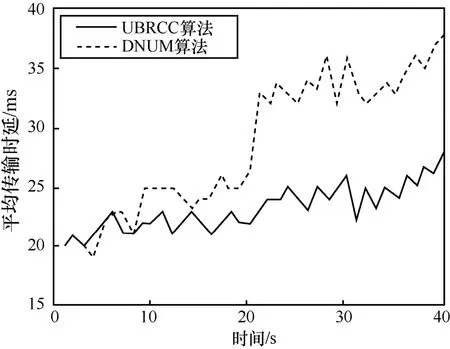
图8 2种算法下的消息传输时延

5）消息产生率

如图9所示，在2种算法的调节下，信道资源根据车辆的安全需求按需分配，数据分组产生率最终收敛至最优。从0 s到20 s，数据分组产生率收敛为7 packet/s。第20 s时，由于车辆密度增大，为避免信道拥塞，消息产生率最终收敛为4 packet/s。从图9可以看出，与DNUM算法相比，在UBRCC算法调节下，数据分组产生率能够更快地收敛至最优，因此性能略优于DNUM算法。

图9 2种算法下的消息产生率

6）算法的收敛性

根据网络效用最大化理论，当目标函数值即效用函数之和最大时，可以求得每辆车的最优数据分组发送速率，从而满足每辆车的安全需求。从图10可以看出，对于 DNUM 算法，目标函数值大约在13次迭代之后收敛至最优，而在UBRCC算法下，目标函数值大约在8次迭代之后收敛至最优，因而性能优于DNUM算法。

图10 目标函数值的迭代过程

6 结束语

在VANET中，信道拥塞会严重影响CVSS的性能。传统的拥塞控制算法依赖信道状态信息将信道负载控制在理想范围之内，没有考虑车辆的安全需求，因而无法做到根据车辆的安全应用需求按需分配信道资源。为了解决这个问题，本文提出了基于网络效用最大化理论的分布式拥塞控制策略。首先，提出了车联网下信道资源分配的网络效用最大化模型，并在该模型中提出了反映车辆安全需求的效用函数；然后，基于该模型，建立了在传输功率固定条件下无线信道资源分配的优化问题，该优化问题以实现所有车辆的效用之和最大化为目标；最后，为了求解该优化问题设计了分布式拥塞控制算法UBRCC。

与控制信道拥塞算法相比，UBRCC算法更加看重单个车辆的安全需求，所以实际信道负载与理想负载之间有时可能会发生偏差。未来工作是设计一种更加顽健的算法来避免这些偏差。另外，下一步的工作会将数据分组发送速率调节与传输功率调节结合起来，重构网络效用最大化模型，提出一种更加综合的信道拥塞控制策略。