基于均方根信息滤波状态空间模型的制造业PMI季节调整

邓光明，詹 婷

（桂林理工大学a.理学院；b.应用统计研究所，广西 桂林 541004）

0 引言

采购经理人指数（PMI）是一套月度发布的且具备综合性的经济监测指标体系，由五个扩散指数即订单、生产、雇员、配送、库存加权而成，是通过对采购经理的月度调查汇总得来的指数，用来反映经济的变化趋势、分析和预测经济走势。作为判断经济扩张与收缩的晴雨表，PMI已广泛应用于相关政策制定、企业活动决策和宏观经济分析等过程，其之重要性不言而喻。制造业采购经理人指数，由于囊括新订单、产量、雇员、供应商配送、库存、价格、进口等多个商业活动方面，在一定程度上受到季节因素的影响，呈现出相应的季节性特征[1，2]。

为了更加准确地揭示指标自身的基本发展趋势、及时反映经济序列短期变化，就必须将季节因素从经济时间序列中剔除，即进行季节调整。季节调整方法主要分为两大类[3]：一类基于模型，另一类基于过滤器。其中，基于结构时间序列模型的季节调整方法，是将结构时间序列模型表示为状态空间模型形式，通过估计模型中的状态向量，最终直接求解出经济时间序列的趋势循环分量、季节分量及不规则分量。该模型特点在于，分解出的各未知成分均具有明确的实际经济含义，且对分量的设定较为灵活、清晰，可解决较为特殊的季节性问题。除了陈飞和高铁梅[4]、侯德鑫[5]、桂文林和韩兆洲[6]分别对GDP、社会消费品零售总额、货币供应量、消费率等宏观经济变量进行了季节调整以外，现阶段国内利用结构时间序列模型对经济时间序列进行季节调整的相关研究并不是很多。

为了剔除季节因素影响，更清晰的反映经济时间序列自身变动规律，本文使用状态空间季节调整模型对我国制造业采购经理人指数进行季节调整研究，在原本Kalman滤波算法的基础上利用均方根信息滤波的方法，对2008年1月至2016年12月我国制造业采购经理人指数序列进行分解，得到制造业PMI的趋势特征、季节效应等成分，并使用Hodrick-Prescott滤波对得到的季节因素进一步分解。

1 均方根信息滤波

均方根信息滤波[7（]SRIF）最早由JPL的学者提出，是Kalman滤波的进化版本，由于均方根信息滤波采用平方根矩阵，其计算元素字长仅需其他算法的一半，并能保证协方差矩阵的对称性及正定性，故具有数值精度高、稳定性强等特点。由于均方根信息滤波理论原理较为冗长，故在此不再赘述。

基于均方根信息滤波的分解可由R软件当中的DECOMP程序包实现。程序命令示例：

Decomp(x,log=TRUE,frequency=12,diff=1,trend.order=1,ar.order=3,seasonal.order=1,trade=TRUE,year=2008,month=1,miss=0,omax=99999.9,plot=TRUE)

其中，x为被分解序列，log为是否对数变换，frequency为一周期内季节数，diff表示差分数，trend.order为趋势阶数，ar.order为AR模型阶数，seasonal.order为季节阶，trade为交易日调整，year为序列初始年，month为初始月，miss表示是否考虑缺失值，omax为数据最大值，plot为分解成分绘图。

2 制造业PMI的季节调整

2.1 数据来源

本文研究样本数据来源于东方财富网（http://www.eastmoney.com/），选取指标为我国2008年1月至2016年12月的我国制造业采购经理人指数，共108个时间点。图1为我国制造业采购经理人指数2008年1月至2016年12月时序图。由图1可看出，PMI指数在2008年经历了一次剧烈的震荡，2009年回升至53.5点后三年内一直呈现持续波动状态。2013年后，波动趋势基本减缓，并于2016年逐步呈现回暖态势。数据区间及样本量已满足季节调整需求，本文季节调整通过R软件实现。

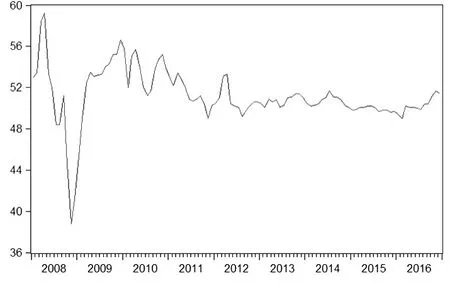
图1 制造业PMI时序图

2.2 交易日模型选择

首先研究SRIF季节调整模型中，考虑交易日影响情况下，不同阶数AR成分的差异性。表1中显示在对应不同的AR模型阶数下，得到的对数似然值LLh、AIC值，作为判断模型优劣的指标，以及σ2、τi(i=0，1，2，3，4)、AR(i)(i=1，2，3，4)的超参数估计结果。

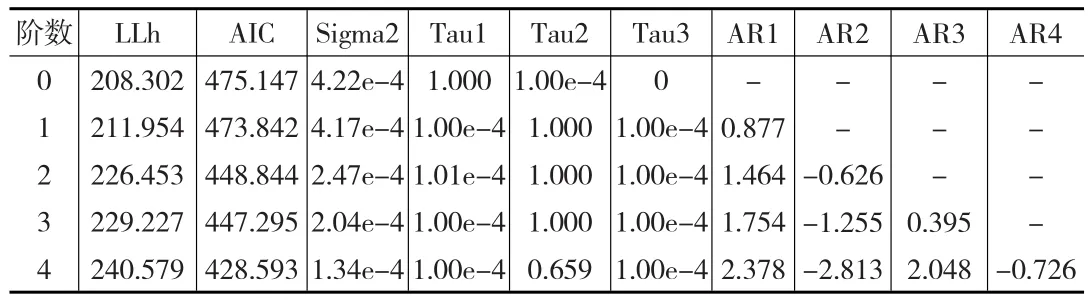
表1 基于SRIF的状态空间季节调整模型AR成分阶选择

由表1可知，当模型中AR成分的阶数为4时，AIC值达到最小为428.593，比不包含AR成分模型（即AR成分阶数为0时）的AIC值小46.554，且此时对数似然函数值取得最大，为240.579。故在考虑交易日影响的情况下可选择4阶AR成分对应的模型，此时模型最优。

2.3 无交易日模型选择

其次，研究SRIF季节调整模型中，考虑AR模型阶影响的情况的情况下，受交易日效应影响及不受交易日影响的差异性。

表2显示在不受交易日效应影响下，对应的不同AR成分阶时的模型结果。对比表1和表2，当AR成分阶数相同时，不受交易日效应影响模型的AIC值比受交易日影响的值更小，且AR成分阶分别取0～4时，两者间的差值分别为13.697、13.821、12.39、12.248、10.494。总体来看，不受交易日效应影响的季节调整模型更优，交易日效应对我国制造业采购经理人指数的影响不甚显著。

表2 基于SRIF的状态空间季节调整模型交易日成分选择

可见，我国制造业采购经理人指数更适合于无交易日季节调整模型，且AR模型阶为4时，模型最佳，对应的AIC值为418.099，对数似然函数值为239.825，模型总体拟合效果较好，通过了所有检验。季节调整后的趋势特征、季节特征如图2、图3所示。

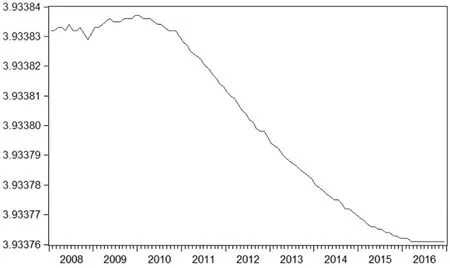
图2 制造业PMI趋势特征图

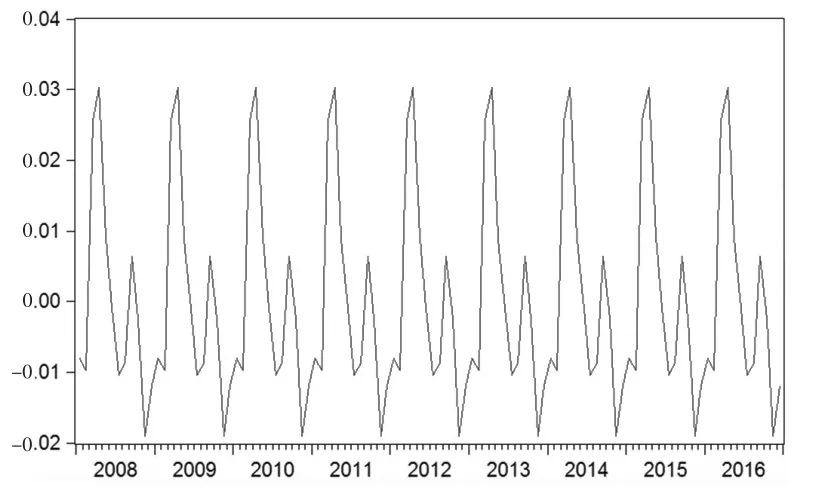
图3 制造业PMI季节特征图

2.4 PMI调整后趋势特征

由图2可见，自2008年1月至2016年12月这一区间内，我国制造业采购经理人指数经季节调整后的整体走势呈现匀速缓慢下降趋势，趋势特征波动区间介于3.93376～3.93384点之间，虽变化值细微，但同样能反映整体波动趋势。

2008年一整年PMI趋势呈现震荡波动趋势，由于受到世界金融危机影响，9月起急转直下，于11月达到这一年的最低点。随着政府出台相应政策来缓解危机影响，如扩大内需、适度放宽货币政策等，使得经济情势有所缓解，PMI趋势短期内逐步震荡回升，于2009年12月达到最最高点，持续一个月。

由于经济危机冲击了我国国内金融、出口贸易、投资需求、房地产市场等方面，在一定程度上阻碍了我国经济的健康快速发展，使得经济增速放缓，在2010—2015年这一段时间内PMI呈现了匀速缓慢下降趋势。2016年3月后，PMI趋势特征保持平稳一直持续到年底。

2.5 PMI调整后季节特征

剔除趋势循环因素及不规则因素之后，可得到2008年一季度至2016年四季度我国制造业采购经理人指数的季节性因素。由图3可看出，我国制造业采购经理人指数的季节特征明显，总体季节性因素对我国制造业PMI指数每年特定季节的影响程度基本相同，从一季度至四季度总体呈现先升后震荡下降的趋势。

一季度快速上升至0.026点，二季度持续减速上升一个月后迅速下降0.031个点，三季度继续下降0.009个点后少量回升，四季度震荡下降，于11月触底后反弹0.007个点。这种季节性影响程度以一年为周期，呈现周期性波动。

1月份至2月份季节趋势下滑主要与春节因素有关，出口订单及库存指标均支撑经济。随后受春节效应影响，旺季将至，群众购买力增强，商品需求量极速扩张，刺激了制造业多个方面，故2、3月份季节效应呈现快速正向影响。二季度延续春节效应的余力，增长效率明显放缓，仅持续了一个月，后开始下降。三季度由于受天气因素影响，强降雨等天气现象影响我国大部分省市，尤其长江中下游部分地区易受洪涝灾害影响严重，对相关地区的生产、运输等造成较大影响。

制造业采购经理人指数季节因素的绝对值环比变化趋势如图4所示，可知季节因素绝对值环比变化同样呈周期性波动，波动幅度基本相同，周期为1年，且保持在-23%～24%之间波动。

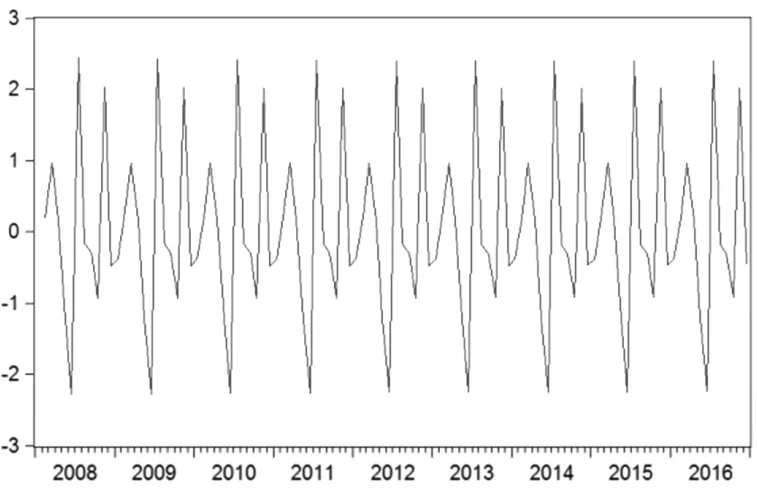
图4 制造业PMI季节因素绝对值环比变化趋势

2.6 PMI季节因素分解

对经季节调整分解后得到的制造业采购经理人指数季节因素使用Hodrick-Prescott滤波来分解，可得到季节性因素的趋势项因素及循环因素，由于是月度数据，所以此处λ=14400，分解后得到的趋势项因素及循环因素如图5所示。

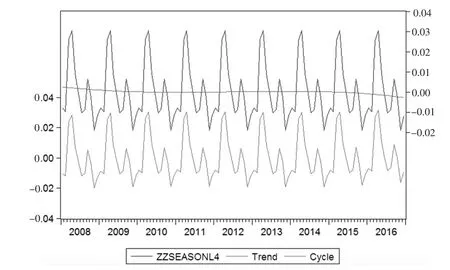
图5 制造业PMI季节因素分解的趋势与循环成分图

由图5可看出，制造业采购经理人指数季节因素的趋势项趋于平滑，表明制造业PMI季节因素保持稳定状态，再次说明每年受到的季节效应影响基本相同。而经HP滤波分解出来的循环因素呈现以一年为周期的波动性，且波动趋势与制造业PMI季节因素的波动趋势相似，表明制造业PMI季节因素变化主要受到循环因素影响。

2.7 与卡尔曼平滑法比较

将制造业采购经理人序列改写成为n阶多项式的状态空间模型，确定季节因子周期，并采用卡尔曼平滑法[8]对序列进行分解得到趋势项及季节因素成分。

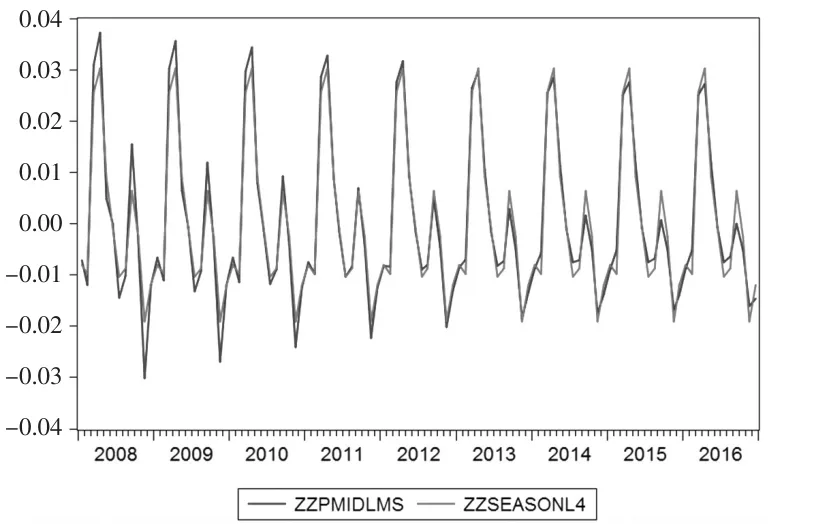
图6与卡尔曼平滑法季节成分对比

图6 为均方根信息滤波分解得到的季节成分与卡尔曼平滑法分解得到的季节成分对比图，由图6可知分解得到的两季节成分波动规律大体相同，但卡尔曼平滑法的季节因素影响呈现由强到逐渐减弱的状态，表明季节因素对制造业PMI的影响程度从2008年开始至2016年是逐渐减弱的。由均方根分解得到的季节成分自2013年起，每年的2月份都会有一个小幅回落，而卡尔曼平滑得到的季节成分并未检测到这一变化。总体看来，均方根分解得到的季节成分精度更高，更稳定。

3 结论

本文对2008年1月至2016年12月的我国制造业采购经理指数序列构建了基于状态空间模型的季节调整模型，在Kalman滤波的基础上采用均方根信息滤波对状态空间季节调整模型进行分解，将我国制造业PMI序列有效分解成趋势、季节、噪音及AR成分，有效估计了模型中的超参数，拟合效果良好。并构造了制造业PMI季节因素绝对值环比增长率。接着，采用Hodrick-Prescott滤波对分解得到的季节性因素进行进一步分解，得到季节效应的趋势项因素及循环因素。通过以上研究，得到如下结论：

（1）总体来看，交易日效应对我国制造业PMI影响不显著，无交易日因素且AR成分阶数为4时，模型最优。

（2）经均方根信息滤波分解，得到的制造业PMI趋势特征呈现波动—短期上升—匀速下降—平稳的状态。且2008年波动较为频繁，2009年少量回升后于2010—2015年持续下降，2016年趋于平稳。

（3）分解得到的季节效应特征明显，以年为周期呈现周期性波动，一季度受春节效应影响，三季度受天气因素影响。

（4）对季节性因素进一步分解，得到季节效应的趋势项因素平稳，循环因素具有波动性，且制造业PMI季节效应主要受循环因素影响。

（5）对比均方根信息滤波及卡尔曼平滑法分解得到的季节成分，可知均方根信息滤波分解得到的成分更稳定，效果更精确。