追问，让数学思维出彩——例谈小学数学教学中的有效追问

⦿蓝雪敏

追问，简单的说就是追根究底的问，是教师根据学生的答问结果及时进行追根溯源的提问。有效的追问是对主问题的补充与深化、延伸与拓展，可以引发学生的再次思考，促进学生再次产生认知冲突和探究的欲望，使学生的思维更深入、更出彩。

一、追问析“错”——拨正思维

教学中，学生出错是常有的事，究其原因大多与数学思维脱不了干系。当学生解答出错、认知出现困惑、理解出现偏差时，教师应及时洞察，以巧妙的追问，找出学生思维出错的原因，探寻学生最真实的原有思维。之后从学生思维的“错”点处入手，及时设计追问，促进学生深入理解知识本源与本质，使学生真正理解掌握。

【案例点击】《分数意义》教学片断：

师：同学们手里有12根小棒，请根据题目要求，取出相应的小棒。

(有的学生拿出了1根小棒；有的学生不知所措；有的学生则充满信心。)

师：你怎么想到拿出1根小棒的？

生1：分子是表示所取的份数，分子是1，就是取出1根。

生2：因为这里的分母并没有告诉我们是多少，所以无法取出小棒。

师追问道：这里的分子1，就是指1根吗？

生：分子表示取的份数。这里是指取1份。这一份是多少根，是要根据把12根小棒平均分成几份来确定的。

师继续追问：是不是真的无法取出小棒？

生1：我认为可以。如果把12根小棒平均分成2份，那么其中的1份就取6根小棒。如果把12根小棒平均分成3份，那么其中的1份就取4根小棒。以此类推。

生2：我也认为可以。关键就是看我们把12根小棒平均分成几份。

上述这两个追问都源于学生认知中出现的混淆与困惑，通过这样的追问，有利于促进学生深入思考，使学生加深对分母、分子表示意义的本质理解。

二、追问激“思”——拨动思维

教学中，教师不仅要做学生学习的铺路架桥者，更要善于激活学生的思维因子，激发他们的求知欲望，促使学生思维不断拓宽、深刻。而追问就是促进学生思维发展的一个触发器，适时有效的追问能拨动学生思维的琴弦，能让学生的思维演奏出美妙的声音。

【案例点击】《正比例的应用》练习

出示：一个打字员计划用1小时打完一份4500字的书稿，她打了15分钟时查看了一下，发现正好打了1230个字，照这样的速度，她能按时完成任务吗？

(学生很快就用正比例求出了实际需要的时间，并得出结论：能按时完成任务)

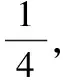
这样的追问，有效地打破了学生的定势思维，激发了学生继续探究的欲望。从而使学生摆脱常规思维的桎梏，尝试着从不同的角度出发，去寻求不同的思维途径，最终拓宽思维广度，促进思维不断深入。

三、追问明“理”——提升思维

教学中，有很多问题学生可能知其然而不知其所以然，因为学生的思维还倾向于感性认知层面。通过有效的追问，能使学生的思维清晰化、明朗化，引发出更深层次的思考。这样学生的思维才会由表及里，实现思维品质的提升。

【案例点击】《认识几分之一》教学片断

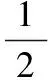
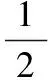
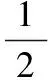
这样的追问，能让学生透过直观形象的感知，将数学思维从直观感性理解的层面，提升到基于知识本质的抽象理解层面，真正实现从思维由浅入深、由表及里的蜕变。

四、追问促“辨”——自纠思维

教学中，易混淆的知识往往容易干扰学生的思维，成为学生思维的障碍点。这种障碍点通过教师的不断讲、反复练，只能短时间内有成效。如果想让学生在理解的基础上掌握，那么设计“辨析比较”环节，在教师不断的追问中，让学生自主纠正原有错误思维，能有效的让学生从根源上杜绝错误的再次发生。

【案例点击】《圆的周长》练习

出示：半圆的周长怎么计算？

(问题抛出，即听到两种声音：大部分认为是圆周长的一半，还有一小部分认为是一条弧加上一条直径。)

针对以上两种声音，老师可追问：这两种想法都正确吗？你们有什么办法可以自己来验证自己的想法？

这一问题抛出后，学生借助画图，将两种想法进行了对比验证。通过验证发现“圆周长的一半就是一条弧，不能围成一个半圆；而圆周长的一半(弧)再加一条直径，就可以围成半圆。”由此得出结论：半圆的周长等于圆周长的一半+直径。

这个过程，学生出现了知识点的混淆，教师并不需要马上介入澄清，而是通过追问，让学生以画图的方式来对比验证，在对比中自主纠正原有思维，达到对知识的理解。这样的追问，既有利于促进学生探究知识本源，又有利于思维明晰可见，使学生能“自识庐山真面目”。

总而言之，有效的追问应以更好地完成教学目标为导向，应以促进学生思维发展为前提，应以引导学生进行有意义的数学活动为目标，其必将使学生的思维之花绚丽绽放！