基于傅里叶级数的潮位优化在加纳特码新集装箱码头项目中的应用
2019-03-12黄亚洲陈金桥
黄亚洲 陈金桥
摘 要:加纳特码新集装箱码头项目处于非洲西部沿海,南面大西洋,施工区海域具有涌浪高度大,周期长的特点。本项目的多波束测量是通过自动验潮站获取潮位,虽然自动验潮站位于防波堤掩护内,但是仍然会受到风浪等外部环境的影响,造成一定的测量误差。本文主要介绍傅里叶法潮位优化在本项目中的应用及分析。
关键词:多波束 傅里叶 潮位优化 Matlab
1.引言
加纳特码新集装箱码头项目工程位于非洲几内亚湾北部加纳港口城市特马(Tema),在首都阿克拉(Accra)以东约26km,大概位置:5°36′45″N,0°0′40″W,成立于2016年7月。本项目中多波束测量时检测各船舶施工效果以及区域回淤及冲刷监测的主要测量手段。而潮位改正作为影响测量结果精度的直接因素,提高潮位数据精度对于多波束测量数据分析具有着重要意义。
加纳特码项目部水深测量中的潮位控制主要采用自动验潮站验潮,为尽量减小风浪等外界因素对潮位测量的影响,自动验潮站被安置于风浪较小的港池内石料出运码头北侧。尽管如此,对自动验潮仪测量的潮位进行分析时,潮位数据依然会有违反涨落潮规律的跳变误差(最大有0.1m以上),分析自动验潮站的潮位获取原理可知,自动验潮仪获取潮位会受船舶航行引起的涌浪、风浪或者回头浪等的影响而造成一定的测量误差。而这种误差亦是不可避免的。为提升多波束测量精度,使测量数据能更加准确反映施工区及其附近海域的水深地形变化,本项目采用了Matlab拟合工具箱中的傅里叶拟合算法对自动验潮站数据进行拟合优化,从而达到减小潮位误差、提高测深成果精度的目的,同时本次试验也采用了Hypack等专业测量分析软件对试验结果数据进行比对分析。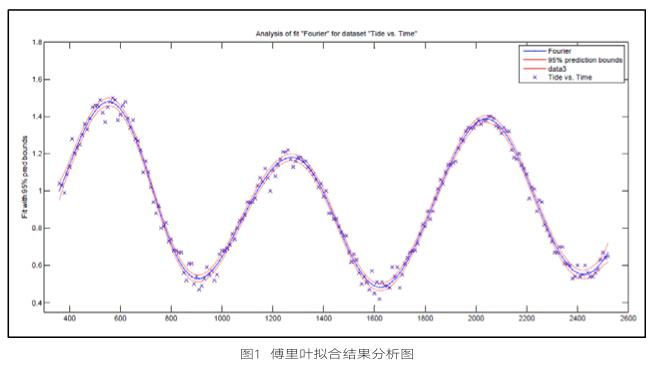
2.潮位获取原理
潮位的获取根据手段的不同,可分为人工验潮、自动验潮站验潮以及 RTK无验潮三种。由于RTK无验潮是在测量过程中实时获取三维坐标信息,并对水深进行实时改正,所以在本文中不予讨论。而本项目采用的验潮方式主要是以自动验潮为主,人工验潮为辅。
人工验潮是一种由验潮员在已知基准点定时测取潮位的手段,人工验潮精度主要受人为读数误差、环境误差的影响。因为受潮汐及涌浪的影响,验潮员验潮时水面经常起伏很大(在近海有掩护的港池内会稍好)。由于以上原因,人工验潮所获取的潮位存在着很大误差,误差的大小主要取决于验潮区域海浪及潮汐的大小。
自动验潮站验潮作为一种无验潮技术之前的主要自动化验潮手段,是通过在已知基准点安装自动验潮仪的方式实时获取并记录潮位。而到目前为止,自动验潮仪的品牌有很多,大致可分为浮子式、压力式和传感式几类(本项目采用传感式验潮仪)。虽然自动验潮仪在设计时一般会通过在一段时间内进行多次采样,并求取平均值的方法来滤除波浪的影响,然而在实际应用中发现,验潮仪所获取的潮位依然存在着一定的误差。

3.潮位数据获取及优化原理
无论是人工获取还是自动验潮站获取的潮位数据都是一种具有潮汐变化特性的离散的时间序列数据,只是当数据获取时由于外界环境或自身(人或验潮仪)的影响,时间节点上的潮位值不可避免得带有测量误差。此时,为了获得更加可靠的潮位数据,需要计算一条既能反映数据整体分布又能反应潮位数据特性的潮位曲线,即采用最小二乘法进行拟合。而因为潮汐的特殊性,选取合适的拟合方法显得尤为重要。
在近海区域潮汐的规律性较强,国内外往往通过对往期潮位数据的分析以及一定的理论研究和计算来获取达到实用化要求的潮汐预报数据。而通过查询特码当地潮汐资料可知,当地潮汐预测使用的是福尔曼算法,潮位预测公式如下: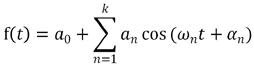
其中a0为平均参考海平面,an为振幅,αn为相位,ωn为角频率。可以看出当地潮位波动可以分解为一系列周期性的三角函数。
而离散傅里叶变换在数字信号处理中起着及其重要的作用。它可以通过对高频扰动信号进行抑制来还原低频的原始信号,具体在本项目中表现为对采集的潮位数据的高频波浪数据进行抑制,从而还原出低频的更接近真实的潮位数据。
而在Matlab拟合工具箱中的傅里叶拟合工具则采用三角形式的傅里叶展开式对数字信号进行拟合。即假设有潮位函数f(t)可展开为如下傅里叶展开式: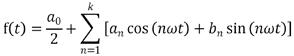
则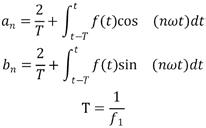
其中f1為基本频率。
4.潮位傅里叶拟合的应用及分析
为提升多波束测量结果数据精度,本项目通常采用Matlab中拟合工具箱中的傅里叶拟合法对潮位进行优化。本文中以两天的潮位为例,对两天的潮位进行优化并分析。所使用潮位数据的时间间隔为10分钟,共217个潮位值,将这些潮位数据按照时间序列导入Matlab数据库中。
在拟合功能模块中,选取傅里叶拟合法对潮位数据进行拟合,在进行算法拟合之后,通过拟合曲线和原始潮位点云分布可看出拟合曲线与原始潮位走势较为符合。优化拟合曲线以及分析结果如图1所示。
将拟合后的潮位与原始潮位进行比对分析,为了进一步更加系统地对拟合优度进行评估,此处采用决定系数R2(R-Square)来进行评估。决定系数表示回归平方和占总离差平方和的比重,用来表示拟合潮位值对实际潮位值的解释程度,即:
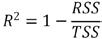
通过上式可知,决定系数正常取值范围为[0,1],越接近1表示该模型对数据的拟合效果越好。但是R2会随样本数量的增多而增大,故进一步采用修正决定系数R12(Adjusted R-Square)来进一步评定:
5.实测多波束数据分析
为了更加直观地分析潮位優化对于多波束测量结果数据的影响,本文将使用同一区域前后两天的多波束测量数据进行处理分析。
具体的比对方法为:在多波束数据后处理过程中分别使用优化前后的潮位数据对两天的多波束数据进行潮位改正。并将得到的两组样本数据通过专业数据分析工具生成三角网并互差后,可得到D1(潮位优化前数据互差)和D2(潮位优化后数据互差)两组差值数据。将两组差值数据进行统计分析后,可得到差值分布图如图3。
由图3中的差值分布图中可以看出优化前后的数据差值都呈正太分布,同时两组差值数据都具有测量误差的有界性(测量误差绝对值有一定的限制,高于限制的概率为零)、聚中性(测量误差越远离期望值概率越低)和对称性(误差呈对称性分布)的特点。然而在经过傅里叶级数进行潮位优化之后,虽然两个差值样本的期望值无明显变化,但是误差样本表现得更为集中,标准差σ更小,精度更高。
经过以上试验发现傅里叶拟合法在潮位优化中的确有着较为显著的表现,不仅潮位曲线拟合度较好,且由经过优化后的潮位对多波束数据进行改正后,测量误差表现得更为集中,测量结果数据的精度有着显著提升。
6.结论
在本项目实际应用中,使用傅里叶潮位优化法对提高测量精度、提升工作效率有着重要的作用。由于误差分布特性,傅里叶潮位优化法在以回淤监测等对精度要求较高的多波束测量中有着尤为显著的作用,去除了潮位扰动的影响,可以更加精确地看出海底回淤或者冲刷的影响。而且在实际应用中发现,傅里叶潮位优化法不仅能滤除高频涌浪误差,还能有效地剔除潮位观测数据中的粗差。
参考文献:
[1]Foreman M G G.Manual for tidal heights analysis and prediction[M].Institute of Ocean Sciences,Patricia Bay,1979.
[2]周玲.MATLAB 在傅里叶变换中的应用[J].运城学院学报,2011(5):29-31.
[3]江海东,费岳军,应岳.使用 MATLAB 拟合工具箱进行潮汐调和分析[J].海洋技术,2012, 31(3):33-36.
