基于差分进化算法的油田开发 二层规划模型求解及应用
2019-03-12侯春华
侯春华
(中国石化胜利油田分公司 勘探开发研究院, 山东 东营 257001)
油气田开发投资高、风险大,需要科学的决策和合理的成本控制,才有可能获得最佳经济效益.文献[1-13]对油田开发规划的数学模型进行了大量的研究,但是,过去的研究主要集中在配产上,以满足市场和国家的需求为主要目标[2-7].由于目前国内大部分油田已进入开发中后期,特别是长期低油价,需要将经营目标从“完成计划生产任务”转变为如何获得最好的经济效益[10-13],这也是一般国际石油公司采取的经营管理模式.Isebor等[8]建立了一个混合整数非线性规划模型来优化开发油田,并通过全局搜索算法来进行求解.
文献[14]建立了一个双层多目标模型来优化油田开发规划的措施结构,但是这个模型并没有被数值求解;王羽等[15]建立一个简单的二层模型来获得最优的配产方案;Vanessen等[16]提出了一个两级战略来提高水驱油田项目的长期经济效益,以实现全周期优化.
在已有的优化模型基础上,本文以工作量和项目投资组合为核心,采用二层规划模型来实现油田中长远开发规划的优化.与传统的单层规划模型或二层规划模型相比,本文针对油田开发规划所采用的二层规划模型、影响因素与评价指标的关联关系是基于油田开发规律的显式表达式,可以更有效地结合油藏工程原理来分析不同层次的指标之间的相互影响.在模型中,上层将投资分配到油田开发的不同开发板块,其目标是实现油田净现值(NPV)最大;下层是在投资和产量约束的条件下,确定最佳工作量组成及最佳项目投资组合.该模型的决策变量包含了整数值和实值变量,因此是一个混合整数非线性二层规划问题,已经证明该问题是一个NP难问题[17].因此,我们引入差分进化算法(DE)设计了一个混合算法来求解该模型.差异进化算法用来估计来自较下层的响应[18],此算法在数值优化中表现出优异的性能.由于从下层到上层的响应的准确性对于算法的有效性是至关重要的,所以文献[19]利用有效集方法和隐式枚举方法来解决下层模型.
1 油田开发二层效益规划模型的建立
二层规划是为了解决分层系统中决策对象的分散决策问题而发展出来的一门学科,它与文献[20-22]提出的竞争模型密切相关.上层决策者被称为领导者,而下层则被称为追随者.不同层次的决策者试图仅通过部分或者完全不考虑其他决策者的目标来实现自身的目标,但是他们对策略的选择却是彼此影响的.以油田开发规划为例,管理者将决定以哪种开发方式进行投资,其目标是以最少的投资获得最大的利润.但是对于采油厂或作业区的决策者来说,他们想获得更多的投资来完成分配的产量目标.这个交互过程可以表述为:
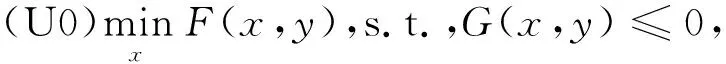
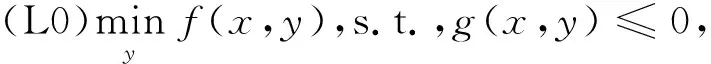
(1)
其中,F,f:Rm×Rn→R,G:Rm×Rn→Rp,g:Rm×Rn→Rq.F(x,y)是上层(U0)的目标函数,x是决策变量的向量.f(x,y)是下层(L0)决策者的目标函数,y是决策变量的向量,并且是每个级别的约束条件.
油田开发规划的二层规划模型可以更明确地反映油田公司不同层级之间(油田公司的管理人员和采油厂或作业区的管理人员)的决策交互作用的过程.
1.1上层模型油田公司由于油藏类型复杂、地面条件多样,一般采用多种开采方式进行开发,如注水、热采和化学驱等.油田开发规划的一个关键问题是确定每种开发方式的投资方式和投资额度.在本文中,油田开发规划二层模型的上层是确定投资的分配,使总净现值最大,并满足生产需求等约束条件.上层规划模型如下:
(2)
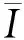
油田计算净现值(NPV)的年限通常取15年评价期,因此来自投资上限为Ii的第i种开发方式的NPV可以通过下面的公式计算:
(1+rd)-t,i=1,2,3,
(3)
其中,P是原油价格,单位为万元/ 107kg,S是商品率,通常为固定的数字0.97,Yi(t)是第t年第i种开发方式的总产量,单位为107kg,Ci(t)是当年第i种开发方式的总成本(万元),Ii(t)是当年对第i种开发方式的实际投资(万元),rd是折现率,Ii(t)应该通过工作量(下层模型)的决策变量,通过(11)和(12)式来计算,而不是Ii.一旦确定了投资分配方案(I1,I2,I3,I4),下层规划应该在第t年不超过Ii的约束下进行建模,如模型(4)所示.
(C1(t)+C1add(t))},
(4)式中的第二个约束条件意味着总产量必须大于最小要求Q.Yi(t)与每年的工作量有关,因此与投资Ii有关,i= 1,2,3,4.第三个约束是指每种开发方式的新增可采储量总量应该满足每年的下限NR.这里NRi与新井数量(即工作量)有关,故也与投资Ii有关.
1.2下层模型基于油田的实际情况,规划对象不同,规划期内投资规模及投入工作量的大小也会不同.如规划对象储量规模小,规划期内新老区产能建设投入项目少,可以提前编制分区块项目方案,由第三方机构对每个项目进行评估(见表1),而开发规划的决策工作是根据所有项目的评价结果决定每年投入哪些项目.对于储量规模大、开发潜力大的项目,规划期内新老区产能建设投入也大,分区块编制项目方案不符合实际,可以根据宏观规律,简化分为新区增量、老区增量,以便管理者在制定开发规划时,注意分配投入、平衡生产任务和可持续发展的要求.由此可见,多项目构成是一个0~1整数规划问题,而新老区增量规划是一个非线性规划问题.
1.2.1新老区增量开发规划模型 油田开发规划中,一般由于水驱及稠油热采油藏储量规模大,规划期内新老区产能建设投入也大,无法提前编制规划期内所有的开发方案,可以分为新区增量、老区增量,按照上级分配的投入,兼顾开发规律和经济指标(净现值、内部收益率等),通过选择适当的决策变量,将开发指标和经济指标关联起来,从而来优化投入构成.对于水驱油藏而言,上述指标都与工作量投入有直接关系,而工作量又可以以新井数量为描述.因此,我们把第t年的新井数量作为模型的决策变量:以u11(t)和u12(t)表示老区的新井数量和新区新井数量水驱油藏.以5年(十三五规划)为一个规划期也可得模型(4).
该模型的目标是获得水驱油田的最大税后利润R1etax.其中P、S的含义同模型(3);老区新井、新区新井、老区老井产量分别为Y11(t)、Y12(t)和Y13(t),于是(2)式中水驱油藏的总产量为Y1(t)=Y11(t)+Y12(t)+Y13(t),这里Y11(t)和Y12(t)与新井数量u11(t)和u12(t)有关,因此与投资有关,但与Y11(t)和Y12(t)不同,产量Y13(t)来自老井,不需要投资.C1(t)是保持水驱油藏正常运行的总费用,参见(24)式计算C1(t).C1add(t)是水驱油田销售税,参见(13)式计算Cadd(t).I11(t)、I12(t)是新钻井u1(t)和u2(t)的计算投资.
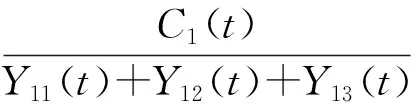
因此,最后一个约束条件的目的是要保证水驱油藏的可持续发展,实现储采平衡.
由于稠油热采的宏观生产规律与水驱油藏类似,因此可以很容易地获得稠油热采的下层开发规划模型:
(C2(t)+C2add(t))},
(5)
(4)式的所有符号(如Y2、u2、I2等)在此模型中具有相同的含义,除了它们是稠油热采油田的变量或参数.C2add(t)是稠油热采油田销售税,104万元,参见(14)式计算C2add(t).不同于模型(4),成本C2(t)包含一个额外的热采成本.
1.2.2多项目构成的开发规划模型 国内大部分油田,如大庆、胜利、长庆、辽河和新疆等,主要以水驱和热力驱为主,兼顾化学驱和气驱等开发方式.化学驱油藏一般投入项目少,已提前编制项目方案,其规划目的是在未来5年内从一批候选项目中获得最佳的项目投资组合.这些候选项目都经过第三方机构进行了准确的评估,如表1所示.
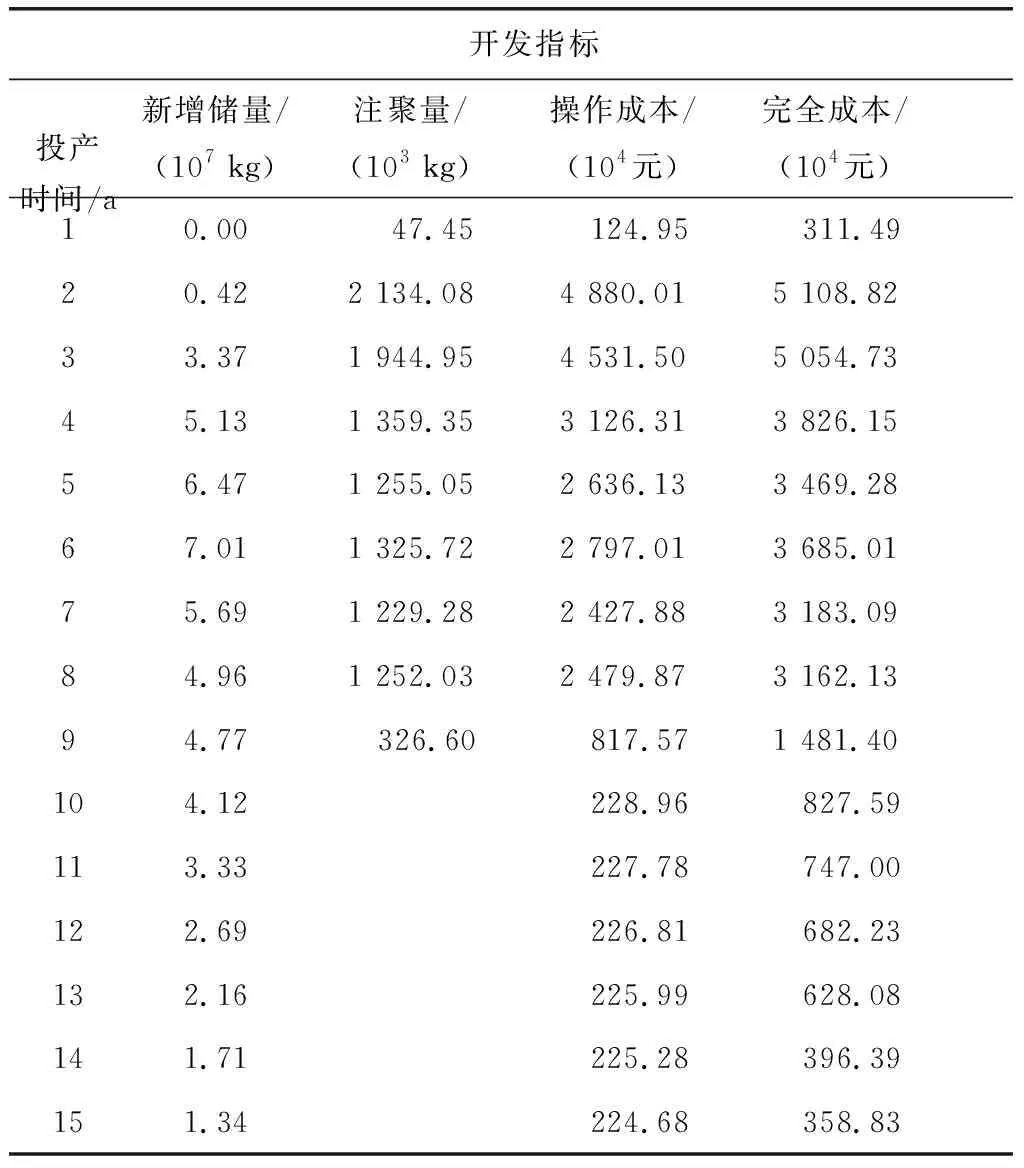
表 1 某油田化学驱项目评价结果简报
注:内部收益率(IRR)为0.77,NPV为28 453.96×104万元,利润为90 893.60×104万元,总投资2 500.00×104万元.
由表1知,按照该化学驱项目的方案进行注聚,可知投产后1~15 a的开发、经济指标情况.其中,第三列表示只在前9 a注入聚合物,后面6 a自然生产,不再注聚;最后一列经济指标全部是按15 a评价期所得的汇总数据.
因此,化学驱油藏开发规划模型实际上是一组0~1规划问题.以xtj(t=1,2,,5,j=1,2,,n)为决策变量,可以得到化学驱油藏的规划模型:
(6)
其中n为化学驱油藏候选项目数.
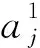
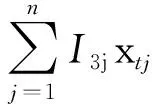
以ytj,t=1,2,,5,j=1,2,,m作为决策变量,可以类似地构建其他类型油藏,如海上板块的规划模型:
(7)
其中m是海上板块候选项目的数量.(7)式的符号具有(6)式相应符号的类似含义.
将模型(2)和(4)~(7)式组合在一起,就可以得到海上开发的二层规划模型.在这个模型中,将上层模型的决策变量I1、I2、I3和I4传递到下层模型成为约束条件.在下层模型中获得的最优解,将反馈给上一层,用以计算目标函数中的NPV.
1.3整体模型求解算法二层规划模型的上层是一个非线性规划问题,其决策变量是实值的.下层模型(4)和(5)式是确定新开采的油井的数量,这是整数,而(6)和(7)式的决策变量是0~1变量,所以该优化模型是一个混合整数非线性二层规划问题,这是一个NP难问题.为了解决这个模型,本节提出了一种混合算法.
差分进化算法(DE)作为一种基于种群的优化算法,具有变异和交叉操作的特点,比遗传算法(GA)更适合解决实值优化问题.采用较常用的DE算法DE/rand/1/bin[23]来解决所给的二层规划问题的上层模型.另一方面,从下层到上层响应的准确性对于有效算法是至关重要的,因此采用有效集方法和隐式枚举方法来解决下层模型(4)~(7)式.这里需要说明的是,虽然(4)和(5)式实际上是一个非线性整数规划问题,但是将其松弛为实值问题所造成的误差,在油田开发规划中是可以接受的.这就是在本文中使用有效集方法来解决(4)和(5)式的原因.于是,可以得到如下混合算法.
步骤1初始化.确定种群大小NP,进化代数T,变异系数F和交叉率CR的值.通过罚函数法将(1)式转化成无约束优化问题.随机生成上层的NP个体Ij=(I1,I2,I3,I4)j;
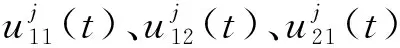
步骤3计算上层的相关变量和适应函数的值.随机选择{Ij1,Ij2,Ij3},进行变异和交叉操作,然后根据文献[23]中的DE/rand/1/bin执行选择步骤;
步骤4如果满足终止标准,则输出结果.否则,请转到步骤2.
2 算例分析
优化的前提是对各项指标的准确性进行预测与计算,对化学驱油藏和海上板块来说,各项目指标都经过了严格评估计算,可以直接使用.但是,水驱和稠油热采则需要结合历史数据分析开发动态,再来进行指标预测.通过对油田开发矿场数据的分析表明,历史拟合的宏观生产规律往往比单井分析更可靠.因为单井生产数据的不确定性在累积过程中会被消除,所以整个油田产量的预测是通过历史数据拟合的各类递减曲线来实现的.以我国东部某油田“十三五”开发规划问题为例,水驱油藏相关指标计算公式如下.
2.1产量预测1) 老区新井的产量
t=1,2,,5,
(8)
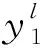
2) 新区新井的产量
t=1,2,,5,
(9)
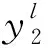
3) 老区老井的产量
i=1,2,,5,
(10)
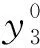
稠油油藏的预测公式具有相同的形式,唯一不同的是递减率λi和初始产量yi的值,i= 1,2,3.
2.2投资的计算1) 老区新井的投资
I11(t)=
(11)
x11是油井的平均深度(m).α11是地面建设成本占投资总额的比例,老区一般为17.6%.
2) 新区新井的投资
I12(t)=
(12)
x11是油井的平均深度(m).α11是地面建设投资总额中的比重,新区一般为18.9%.
稠油油藏的公式形式相同,唯一不同的是井深x2i和地面建设投资总额中的比重α2i的值,i= 1,2.
2.3销售税的计算对于水驱油田和稠油热采油田,销售税率相同,因此C1add(t)和C2add(t)具有相同的形式:
C1add(t)=rs×(Y11(t)+Y12(t)),
(13)
C2add(t)=rs×S×(Y21(t)+Y22(t)),
(14)
其中,rs为销售税率,Y11(t)、Y12(t)分别为水驱油田老区新井产量与新区新井产量,Y21(t)、Y22(t)分别为稠油热采油田老区新井产量与新区新井产量.
2.4完全成本计算水驱油藏水驱油藏的完全成本C1(t)包含3个部分:
C1(t)=电费+折旧/消耗+(手续费+人工成本+杂项费用).
因此,必须逐个计算来获得C1(t):
1) 水驱油藏新钻井的电费(老区为C11p,新区为C12p)
(15)
(16)
其中,d是生产天数,w1i是老区第i年的含水上升率,w2i是新区第i年的含水上升率.
2) 水驱油田新井的折旧/耗损.为了获得折旧/消耗,需要首先计算老、新区的新增可采储量:
NR11(t)=
(17)
NR12(t)=
(18)
因此,老区和新区的新钻油井的折旧/损耗(C11d、C12d)为:
(19)
(20)
3) 水驱油藏(处理费+人工费+杂项费用).老区新井和新区新井的(处理费+人工费+杂费)(C11h、C12h)统一为:
(21)
(22)
这里的积累的起始时间是2001年.
稠油热采的完全成本C2(t)与水驱油藏的形式相同,只是增加了热采成本.对于老区和新区,总热采成本为:
Cs(t)=
cs×TS×(u21(t)+u22(t)),
(23)
其中,cs为吨蒸汽费用(万元/107kg),TS是每年注入蒸汽量(107kg).
综上,水驱、稠油热采的完全成本的计算公式分别为:
C1(t)=
C11p+C12p+C11d+C12d+C11h+C12h,
(24)
C2(t)=C21p+C22p+C21d+
C22d+C21h+C22h+Cs,
(25)
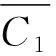
整个油田总投资上限为106万元.海上板块和化学驱板块每年投资的下限分别为2×105万元和6×103万元.有8个海上候选项目和5个化学驱项目.运行上述混合算法,得到以下的整体结果.
表4~6中1、0分别表示该项目在对应的年份投资或者不投资.
从表2可以看出,与水驱开发方式相比,稠油热采的开发效果不如水驱的好,优化结果表明,只有投资的下限分配到稠油板块.化学驱板块情况也是如此,这与该油田实际情况是一致的.表3~6列出了4个下层模型的优化结果.
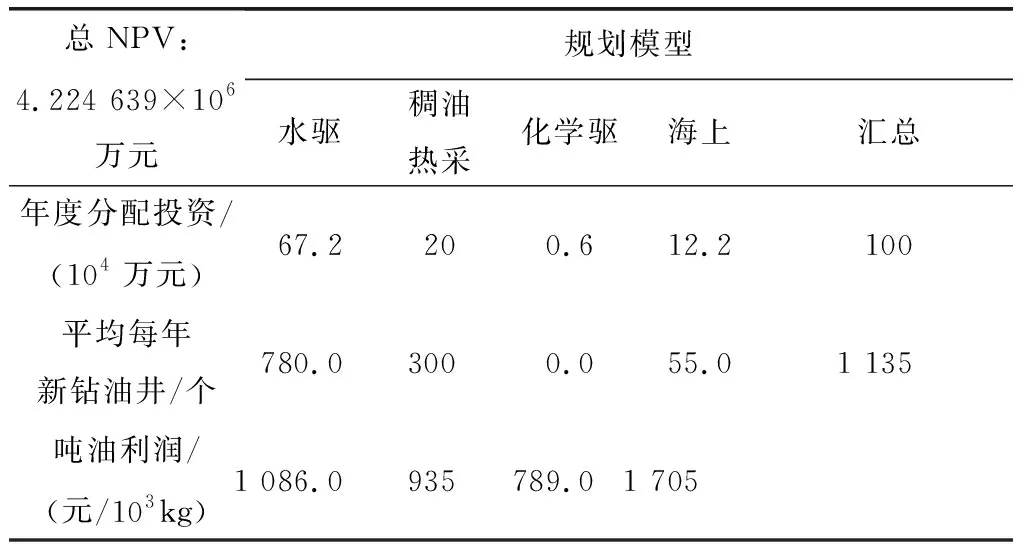
表 2 整体优化结果
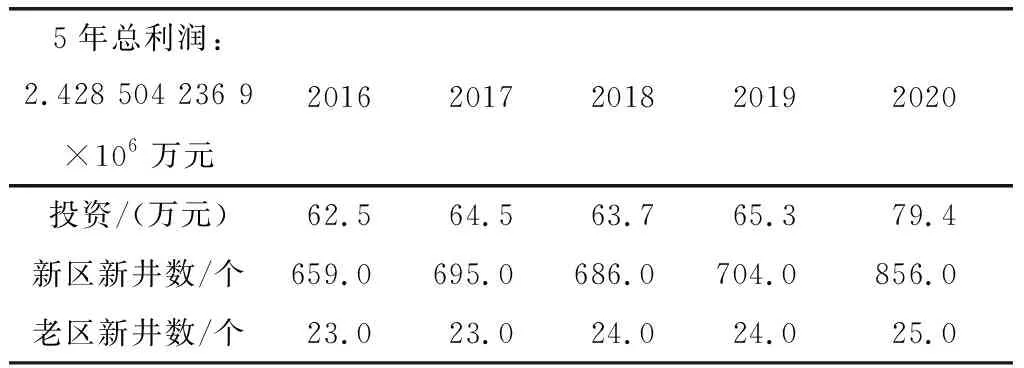
表 3 水驱油藏的下层优化结果
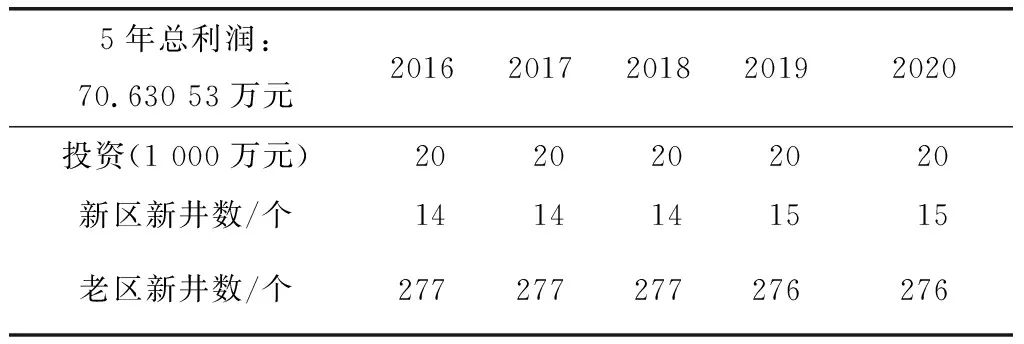
表 4 稠油油藏的下层优化结果
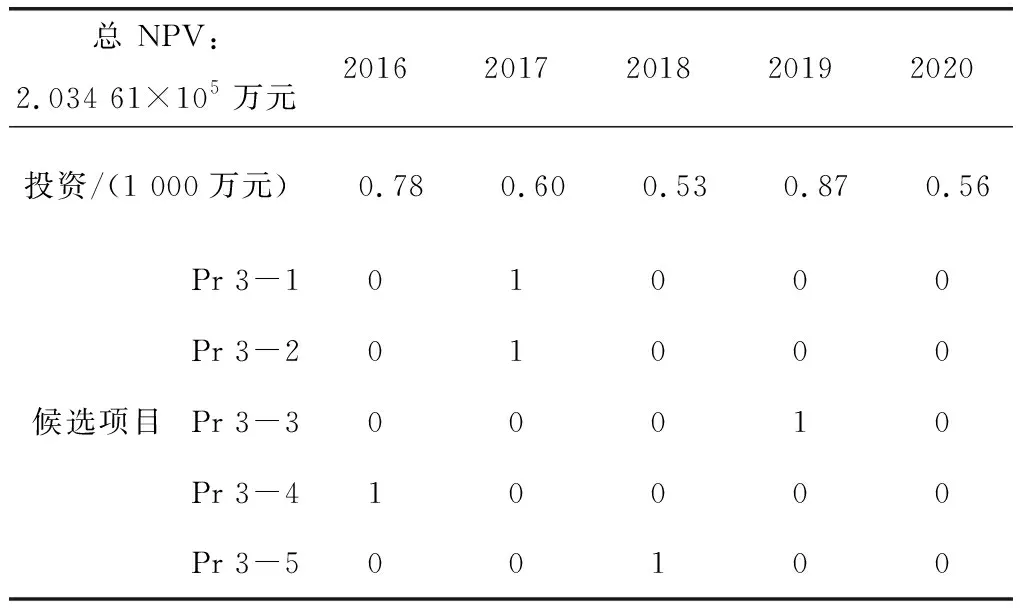
表 5 化学驱油藏的下层优化结果
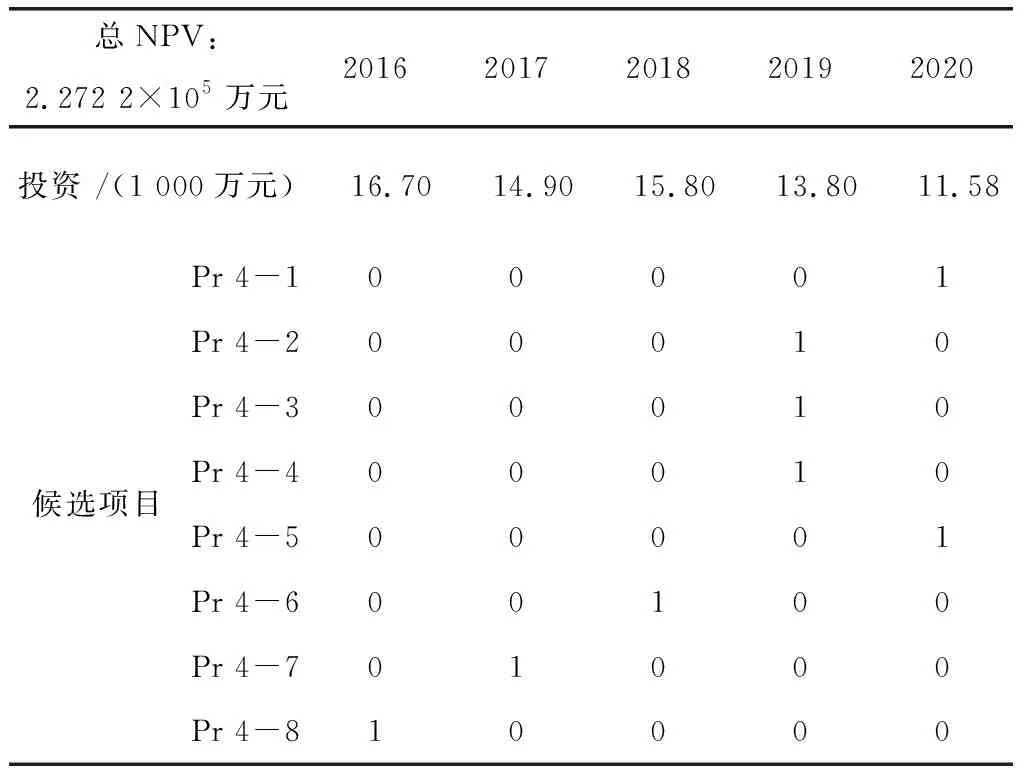
表 6 海上油藏下层优化结果
本文所建模型的敏感性分析可以通过改变优化模型中的参数来完成.值得一提的情况是优化后的水驱油藏NPV和产量对单井投资的敏感性对比,即对新井钻井成本的敏感性分析(见图1).
从图1可以看出,在固定投资限额下,随着单井成本的增加,新开采的油井数量将减少,进而导致总产量下降.但是,NPV却在增加.这意味着新井投资越少,反而效益越好.这一现象说明,水驱油藏的投入产出比开始越来越差,这符合中后期水驱油藏的实际情况.
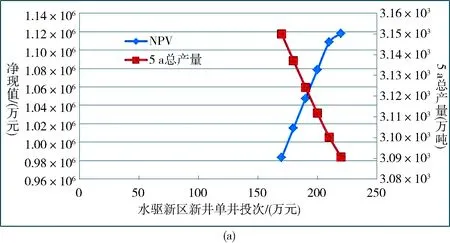
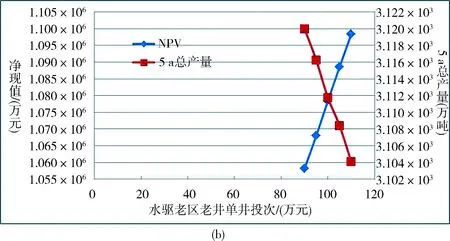
图 1 水驱油藏五年总产量、净现值随单井投资的变化情况
3 结论
本文针对油田开发规划形成了以新老区增量构成和项目构成为底层、以开发方式构成为上层的两层效益规划优化方法, 实现了不同开发方式之间、同一开发方式新、老区增量之间不同对象的整体优化决策.该模型既考虑了油田的整体效益,又考虑了不同开发方式的工作量分配.
1) 多项目构成优化模型可应用于海上、化学驱等多个项目方案编制工作已完成的规划优化,同时可应用于年度产能建设项目的优选.
2) 新老区增量优化模型可用于陆上水驱、稠油热采等规模油田的中、长远开发规划编制, 形成了基于整体规律和关系的新老区增量构成优化方法,实现了宏观规律约束下开发方式内部的优化.
