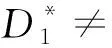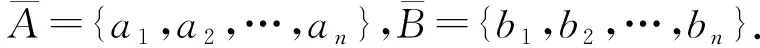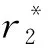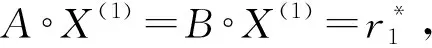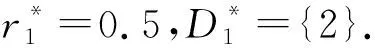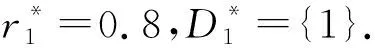max-T合成模糊双线性关系方程的解集
2019-03-12王玉利熊清泉
王玉利, 熊清泉
(四川师范大学 数学与软件科学学院, 成都 四川 610066)
模糊关系在模糊系统的讨论中有着重要的地位,模糊关系方程则是模糊关系研究的主要内容之一.模糊关系方程的求解问题在实际中的应用非常广泛,所以有不少学者对模糊关系方程求解问题进行了深入研究,也得到了丰富的结论.基于对模糊关系方程的研究成果,部分学者也对双线性方程的求解及性质做了研究[1-7].从有限到无限、从单位区间[0,1]到完备格都给出了一些结论.1987年,汤服成[1]首先对max-min合成模糊双线性方程作了详细论述,并且获得了方程在[0,1]上的最大解及解的一些性质.之后研究者开始研究max-min以及max-·合成模糊双线性关系方程.基于汤服成[1]提出的最大解的求法,Li[2]和余布雷等[3]也相继提出了最大解和最大结果的简单算法.1991年,李文议[4]讨论了一类格上的双线性方程,分别讨论当背景格为有限时,求出了方程的全部解;当背景格为无限时,确定了模糊双线性方程的最大解.2005年,余布雷等[5]在[0,1]上讨论了无限双线性方程的性质及其解集.之后,何春花等[6]和张琳[8]对解的一些性质作了拓展.在实际中,模糊关系方程可应用到多个领域.因此确定模糊关系方程的解集不仅在理论上,而且在实际应用中同样重要[9].但一般的max-T合成模糊双线性方程现有文献未作研究.本文围绕[0,1]上max-T合成模糊双线性方程进行讨论,其中T是伪t-模.讨论在有限情况下双线性方程的最大解、极小解的通用形式以及极小解个数和方程的最大解与最大结果的求法.
1 预备知识
为了讨论方便,下面给出一些定义和基本结论.假设L=[0,1],I={1,2,,m},J={1,2,,n}.
定义1.1[10]如果L×L→L上的映射T满足:∀a,b,c∈L,
1) 交换律:T(a,b)=T(b,a);
2) 结合律:T(a,T(b,c))=T(T(a,b),c);
3) 单调性:b≤c⟹T(a,b)≤T(a,c);
4) 有界性:T(a,1)=a,
则称T为L上的t-模.
定义1.2[11](i) 如果L上的一个二元算子T满足∀a,b,c∈L和
(T1) T(1,a)=a,T(0,a)=0;
(T2)b≤c⟹T(a,b)≤T(a,c),
则称T为L上的伪t-模.
另外,如果T还满足下述条件,则称T分别为无限∨-分配伪t-模和无限∧-分配伪t-模:
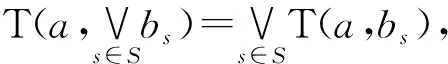
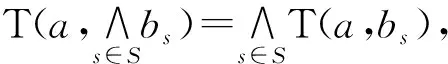
(ii) 如果L上的一个二元算子I满足∀a,b,c∈L和
(I1) I(1,b)=b,I(0,b)=1;
(I2)b≤c→I(a,b)≤I(a,c),
则称I为L上的一个蕴涵.
另外,如果I还满足下述条件,则称I分别为无限∨-分配蕴涵算子和无限∧-分配蕴涵算子:


记T(L)(I(L))为L上所有无限分配的伪t-模T(蕴涵I)构成的集合.如果伪t-模T(蕴涵I)既是无限∨-分配的又是无限∧-分配的,则称伪t-模T(蕴涵I)是无限分配的.
定义1.3[12]设φ:L×L→L,定义Iφ、Lφ如下:
∀a,b∈L, Iφ(a,b)=sup{x∈L:φ(a,x)≤b},
Lφ(a,b)=inf{x∈L:φ(a,x)≥b}.
假定空集的最小上界为0,最大下界为1.
定义1.4[12]设T为有界偏序集(L,≤)上的一个伪t-模,则称部分映射T(a,·)为极大满的当且仅当∀a∈L,{T(a,x):x∈L}=[0,a].
定义1.5[7]设A=(aij)I×J,B=(bij)I×J,X=(xj)J×1,其中aij,bij,xj∈L,称
A∘X=B∘X
(1)
为L上的模糊双线性方程,其中“∘”是max-T合成,T是伪t-模,即
∀i∈I.
注1.11) 记X={X:A∘X=B∘X},称X为A∘X=B∘X的解集.显然X≠∅恒成立.事实上,X=0就是方程(1)的一个解.以下讨论X≠{0}的情况.
2) 令R={r:A∘X=B∘X=r,∃X∈X}.设X∈X,记A∘X=B∘X=r,称r是与X相关的结果.设r∈R,Xr={X:A∘X=B∘X=r}.
显然,设r∈R,方程(1)等价于

(2)
下面假定T∈T(L),∀a∈L,T(a,·)为极大满的且T(1,a)=T(a,1)=a,T(0,a)=T(a,0)=0.
引理1.1[13]设a,b∈L,如果a≤b,则
IT(a,b)=1.
引理1.2[13]设a,b∈L,则
{x∈L:T(a,x)≤b}=[0,IT(a,b)].
引理1.3[13]如果a,b∈L且a≥b,则
{x∈L:T(a,x)≥b}=[LT(a,b),1].
引理1.4[13]如果a,b∈L且a≥b,则
sup{T(a,x):T(a,x)≤b,x∈L}=
inf{T(a,x):T(a,x)≥b,x∈L}=b.
引理1.5[13]∀a,b∈L,
{x∈L:T(a,x)=b}≠∅
当且仅当a≥b.进一步,
{x∈L:T(a,x)=b}=∅
或{x∈L:T(a,x)=b}=[LT(a,b),IT(a,b)].
定理1.1设a,b,c∈L,则以下3个条件等价:
1)b≤c⟹T(a,b)≤T(a,c);
2) T(a,b∨c)=T(a,b)∨T(a,c);
3) T(a,b∧c)=T(a,b)∧T(a,c).
证明1)⟹2) 设a,b,c∈[0,1],因为
b≤c⟹T(a,b)≤T(a,c),
所以T(a,b)∨T(a,c)=T(a,c)=T(a,b∨c).
2)⟹1) 由于T(a,b)≤T(a,b)∨T(a,c)=T(a,b∨c),又因为b≤c,所以T(a,b∨c)=T(a,c),则有T(a,b)≤T(a,c).故1)与2)等价.同理可证1)与3)等价.
以下假设A=(aj)j∈J,B=(bj)j∈J.给定r∈R,令IT(A,r)=(IT(aj,r))j∈J,
IT(B,r)=(IT(bj,r))j∈J
和
IT(A,r)∧IT(B,r)=[IT(aj,r)∧IT(bj,r)]j∈J.
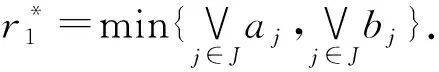

证明假设X=(xj)j∈J为(2)式的解,即
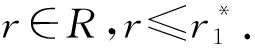

证明由于

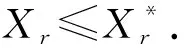
证明设Xr=(xj)j∈J∈Xr,那么


推论1.2设r∈R,则方程


xj∈[LT(aj,r),IT(aj,r)].

xj∈[LT(aj,r)∨LT(bj,r),IT(aj,r)∧IT(bj,r)],






2 双线性方程A∘X=B∘X=r的极小解
下面讨论双线性方程极小解的形式以及极小解的个数.
定义2.1设S为一偏序集P的非空子集,a∈S.若不存在x∈S使x 注2.1由定义2.1,X*∈X是X的极小元当且仅当∀X∈X,X≤X*蕴含X=X*. 注2.2显然r=0时,Xr的极小元为零.下面讨论Xr中的非零极小元. 设r∈R{0},Xr=(xj)j∈J∈Xr,记Nr(Xr)={j∈J|T(aj,xj)=r}和 Mr(Xr)={j∈J|T(bj,xj)=r}, 把Nr(Xr)和Mr(Xr)简记为Nr(X)和Mr(X),把Nr(Xr*)和Mr(Xr*)简记为Nr(X*)和Mr(X*). 定理2.1如果r∈R{0},则Xr都有极小元. 1) 若Nr(X)∩Mr(X)=∅,取s∈Nr(X),t∈Mr(X),定义X*(s,t)=(xj*)j∈J,其中xj*满足 (3) 由引理1.5知T(as,LT(as,r))=r.再由t∈Mr(X)知T(bt,xt)=r,故xt∈[LT(bt,r),IT(bt,r)].又因为Nr(X)∩Mr(X)=∅,则t∉Nr(X),所以T(at,xt) r∨[T(at,LT(bt,r))]=r. 由Nr(X)∩Mr(X)=∅且t∈Mr(X),所以T(at,xt*) r=T(as,xs)=T(as,xs*)=r, 即xs∈{x∈L:T(as,x)≥r}.同理有r=T(bt,xt)=T(bt,xt*)=r,即xt∈{x∈L:T(bt,x)≥r}.由于xs*=LT(as,r)=inf{x∈L:T(as,x)≥r}≤xs且xt*=LT(bt,r)=inf{x∈L:T(bt,x)≥r}≤xt,于是Xr≥X*(s,t).因此Xr=X*(s,t),即X*(s,t)是Xr中的极小元. 2) 若Nr(X)∩Mr(X)≠∅,取k∈Nr(X)∩Mr(X),定义X*(k)=(xj*)j∈J,其中xj*满足 (4) 由引理1.5知T(ak,LT(ak,r))=r,又因为k∈Nr(X)∩Mr(X),则T(ak,xk)=T(bk,xk)=r.由引理1.5有xk∈[LT(ak,r),IT(ak,r)]且 xk∈[LT(bk,r),IT(bk,r)], 所以T(bk,LT(ak,r))=r.进一步有 T(ak,LT(ak,r))∨0=r, =T(bk,LT(ak,r))∨0=r, 即X*(k)∈Xr.设Xr=(xj)j∈J∈Xr且Xr≤X*(k),当j≠k有xj=0.因此仅需证明当j=k时,xk=xk*=LT(ak,r).事实上, 因此r=T(ak,xk)=T(ak,xk*)=r,即xk∈{x∈L:T(ak,x)≥r}.由于 xk*=LT(ak,r)=inf{x∈L:T(ak,x)≥r}≤xk, 于是Xr≥X*(k).因此Xr=X*(k),即X*(k)是Xr中的极小元. 定理2.2如果r∈R{0},则Xr中所有的极小元都有(3)或(4)式的形式. 1) 若Nr(X)∩Mr(X)=∅,取s∈Nr(X),t∈Mr(X),定义X*(s,t)=(xj*)j∈J,其中xj*满足 显然X*(s,t)∈Xr且X*(s,t)≤Xr.因此由Xr的极小性有X*(s,t)=Xr. 2) 若Nr(X)∩Mr(X)≠∅,取k∈Nr(X)∩Mr(X),定义X*(k)=(xj*)j∈J,其中xj*满足 显然X*(k)∈Xr且X*(k)≤Xr.因此由Xr的极小性有X*(k)=Xr. 定理2.3如果r∈R{0},则对任意Xr∈Xr,存在极小元X*∈Xr使得X*≤Xr. 证明设Xr=(xj)j∈J∈Xr,则 1) 若Nr(X)∩Mr(X)=∅,取s∈Nr(X),t∈Mr(X),定义X*(s,t)=(xj*)j∈J,其中xj*满足 显然X*(s,t)∈Xr,由定理2.2知X*(s,t)是Xr中的极小元.下面仅需证明X*(s,t)≤Xr.当j≠s,t有xj*=0,因此仅需证明当j=s时, xs≥xs*=LT(as,r); 当j=t时,xt≥xt*=LT(bt,r).如果j=s,由T(as,xs)=r,即xs∈{x∈L:T(aj,xj)≥r}.因此xs*=LT(as,r)=inf{x∈L:T(aj,xj)≥r}≤xs.同理如果j=t时,xt*≤xt,即证得X*(s,t)≤Xr. 2) 若Nr(X)∩Mr(X)≠∅,取k∈Nr(X)∩Mr(X),定义X*(k)=(xj*)j∈J,其中xj*满足 显然X*(k)∈Xr,由定理2.2知X*(k)是Xr中的极小元.下面仅需证明X*(k)≤Xr.当j≠k有xj*=0,因此仅需证明当j=k时,xk≥xk*=LT(ak,r).如果j=k,由T(ak,xk)=r,即xk∈{x∈L:T(aj,xj)≥r}.因此xk*=LT(ak,r)=inf{x∈L:T(aj,xj)≥r}≤xk,即证得X*(k)≤Xr. 定理2.41) 若Nr(X*)∩Mr(X*)=∅,则(2)式的极小解个数为|Nr(X*)||Mr(X*)|. 根据排列组合共有|Nr(X*)||Mr(X*)|种情况,所以极小解的个数为|Nr(X*)||Mr(X*)|. 2) 不妨假设 Nr(X*)∩Mr(X*)={j1,,jk}, 即有{j1,,jk}⊆J使T(aji,xji)=T(bji,xji)=r,那么极小解X*=(xj*)j∈J在xji处取LT(aji,r),ji∈{j1,,jk},因此有k种取法.在J{j1,,jk}中,与1)同理.所以当Nr(X*)∩Nr(X*)≠∅时,方程A∘X=B∘X=r的极小解个数为 例2.2设A=(1,0.8,0.5,0.3),B=(0.4,0.8,0.3,0.5),r=0.5,求方程A∘X=B∘X=r的极小解与解集,其中“∘”表示“max-Lukasiewicz”合成,即TL(x,y)=0∨(x+y-1). 例2.3设A=(0.6,0.2,0.7),B=(0.9,0.7,0.6),r=0.6,求方程A∘X=B∘X=r的极小解与解集,其中“∘”表示“max-min”合成. 所以方程A∘X=B∘X=r的极小解个数为2,全部极小解为v1=(0.6,0,0)T,v2=(0,0,0.6)T.从而由推论1.3知方程的解集Xr={(0.6,[0,0.6],[0,0.6])T,([0,0.6],[0,0.6],0.6)T}. 由推论1.2知,若方程(2)有解,则一定有最大解.记r*是R中的最大元,X*是Xr中的最大元. 定理3.1A∘X*=B∘X*=r*. 证明因为r*∈R,所以存在X∈X使得A∘X=B∘X=r*.由定理1.4知X≤X*,则有A∘X*≥A∘X=r*,B∘X*≥B∘X=r*,即A∘X*=B∘X*≥r*.又由r*的最大性可知A∘X*=B∘X*=r*. 证明必要性 则 则 由推论1.2知X(1)=X(a)∧X(b)是方程的最大解. (5) (6) 下面给出方程(1)最大结果与其对应的最大解的算法步骤. 例3.1求例2.1中A∘X=B∘X的最大结果与其对应的最大解. 例3.2求例2.2中A∘X=B∘X的最大结果与其对应的最大解. 例3.3设A=(0.7,0.2,0.1,0.3),B=(0.9,0.6,0.3,0.2).求方程A∘X=B∘X的最大结果与其对应的最大解,其中“∘”表示“max-product”合成. X(3)=(IT(0.7,0.3)∧IT(0.9,0.3), (IT(0.2,0.3)∧IT(0.6,0.3),1,1)T= (1/3,1/2,1,1)T.






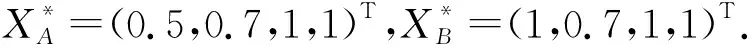

3 双线性方程A∘X=B∘X的最大结果与其对应的最大解