一个具有双线性发生率的随机SIR传染病模型的 动力学性质
2019-03-12李明山张渝曼刘秀敏周效良
李明山, 张渝曼, 刘秀敏, 黄 鑫, 周效良*
(1. 南京航空航天大学 理学院, 江苏 南京 211106; 2. 岭南师范学院 数学与统计学院, 广东 湛江 524048)
1 引言及预备知识
SIR传染病模型在传染病的防控研究当中具有重要作用,自1927年 Kermack等[1]提出SIR模型以来,传染病模型得到长足的发展,许多传染病模型和与其相关的理论被用于分析各种各样的传染病问题[1-28].这些传染病模型大致可以分为2类,即确定模型和随机模型,对于确定模型已有许多优秀成果[2-5,23-25].随机传染病模型在研究传染病传播机理具有重大作用,在现实生活中,环境噪声无处不在,研究环境噪声对传染病传播的影响在传染病的防控中是非常重要的.王克[28]指出传染病模型中的每一个参数都会受到环境的随机干扰,在某种程度上表现为随机波动.例如传染病模型中的接触率和疾病死亡率会受到诸如生物个体的年龄、性别、体质、心情以及气候、季节等因素的随机干扰.而确定模型并没有考虑这些随机因素,只能在一定程度上大致反映传染病传播的真实情况.应用随机微分方程来研究传染病动力学能更好地拟合实际情况,Arnold等[19]和May[20]首先在这方面做出了奠基性工作,随后国内外涌现出大量的研究成果[6-11,13-15].随机传染病模型基本保持了连续传染病模型的基本特征,还可以应用计算机进行模拟,有利于进一步研究传染病的传播机制从而揭示随机传染病模型的动力学性质和生物学意义,为人们预防和控制传染病提供一些理论依据和策略.
文献[21-22]研究了如下具有双线性发生率连续传染病SIR模型
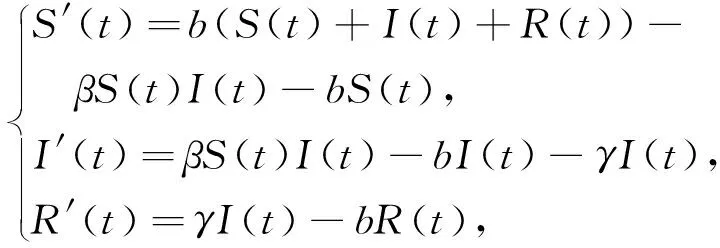
(1)
这里,S、I、R分别代表易感者、染病者、康复者,β>0是感染率,b是出生率并且等于死亡率,γ是康复率.本文将研究SIR传染病模型(1)的随机情形.文献[22]假设—群体总数保持常数N,即
S(t)+I(t)+R(t)=N.
实施尺度变换
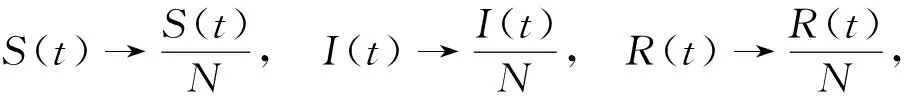
(2)
即对所有的时间t有
S(t)+I(t)+R(t)=1.
(3)
系统(1)可变为
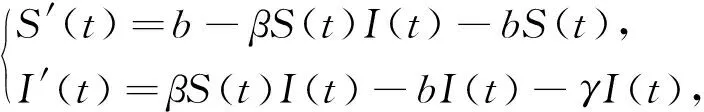
(4)
其中系统(4)有2个平衡点,其中一个是无病平衡点E0(1,0),另外一个是地方病平衡点
用β+σB(t)代替β,这里B(t)表示标准的布朗运动,σ2表示布朗运动的强度.采取标准的布朗运动作为模型的随机扰动是因为标准布朗运动考虑到各种至关重要的数据,同时也因为模型的参数是随着环境的改变而改变的,因此考虑将环境的波动引入模型(4)中,将参数β看成一个随机变量,这样β能够将模型受到环境白噪声的影响体现出来.所以用β+σB(t)代替β,得到如下随机SIR模型
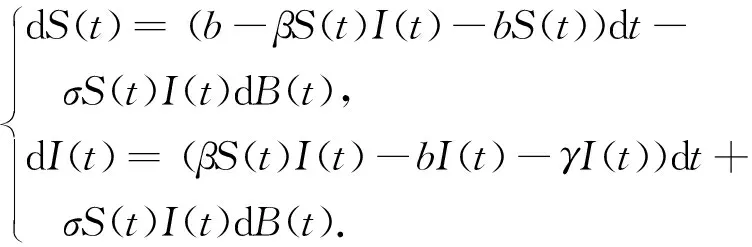
(5)
2 系统(5)正解的存在唯一性
因为S(t)和I(t)分别表示在时刻t易感者和染病者群体的规模,所以它们必须是正的,为了进一步的研究,首先应该给定某些条件使得系统(5)存在唯一的正解.
定理2.1对任意的初值
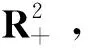
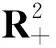
这里τ指的是爆破时间[16].为了证明上述局部解是全局的,只需证明τ=+∞,a.s.,因此定义停时[16]
τ′=inf{t∈(0,τ):S(t)≤0或I(t)≤0},
从τ′的定义易知inf ∅=+∞,可以得到τ′≤τ,如果能够证明τ′=+∞,a.s.,就可以得到τ=+∞,a.s.,由此即可得到
假设τ′<+∞,则存在一个常数T>0,使得
P{τ′
定义C2函数
σI(t)dB(t)+σS(t)dB(t)≥
记
故可以得到
dV(S(t),I(t))≥G(S(t),I(t))dt-
σI(t)dB(t)+σS(t)dB(t).
(6)
在不等式(6)的两边从0到t积分有
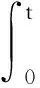
(7)
记(S(τ′),I(τ′))=(0,0),有
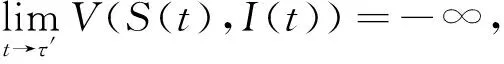
在不等式(7)中令t→τ′,有
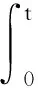
(8)
这就产生矛盾.因此可以得到τ′→+∞,这也证明了S(t)和I(t)不会在有限时间内爆破是依概率1的,定理2.1证毕.基于定理2.1的证明过程可以知道系统(5)的正向不变集为
Π={(S,I):S>0,I>0,S+I≤1}.
因此在下文只需考虑系统(5)在
Π={(S,I):S>0,I>0,S+I≤1}
内的解即可.
3 传染病消亡的充分条件
定理3.1设(S(t),I(t))是系统(5)初值为(S(0),I(0))∈Π的解,有
(9)
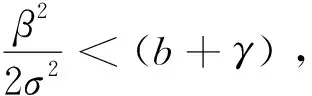
引理3.1设M(t):t≥0是一个具有初值为M(0)=0的局部连续鞅,〈M(t)〉是M(t)的二次变差,令δ>1,γn、τn是2个正项序列,则对几乎所有ω∈Ω,存在一个正整数n0=n0(ω),使得对∀n≥n0有
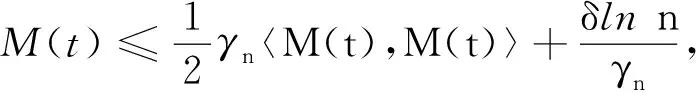
(10)
定理3.1证明对系统(5)应用It公式有
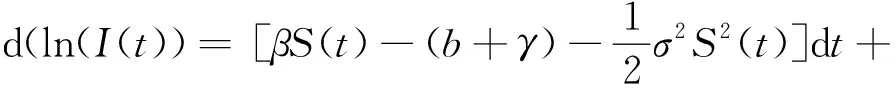
(11)
对(11)式两边从0到t积分得
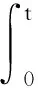
(12)
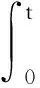
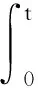
(13)
在引理3.1中选取δ=2,γn=γ和τn=n,对几乎所有的ω∈Ω,存在一个正整数n0=n0(ω)使得对任意的n≥n0有
(14)
由(12)和(14)式可得
lnI(t) (15) = (16) ≤ (17) (18) 故可以得到 (19) 所以对任意的n-1≤t≤n,在不等式(19)两边同除t得到 (20) 令n→+∞,从而t→+∞,由此有 (21) 令γ→0,则有 (22) (23) 由常数变易法有 (24) 定理4.1如果有 (25) 则对任意初值(S(0),I(0))∈Π,系统(5)的解有如下性质 (26) 定理4.1证明 (27) (28) (29) 其中 (30) σS(t)(I(t)+1)dB(t)≥ (31) 对不等式(31)两端从0到t进行积分 (32) 化简得 (33) 由定理2.1可以知道-∞ (34) (35) 故由文献[13]可知,传染病在条件(35)式下在均值意义下是持久的,定理4.1证毕. 根据R0的表达式,可以初步得到以下防控思路和措施:调整R0中的有关参数,使R0尽可能小,为此可以采取下面措施: 1) 研发高效专门传染病疫苗,高效疫苗使得治愈率γ高,R0就越小,传染病的可能性就会变大; 2) 在学校、超市、市场等人口密集地方实施严密监控和防范措施,在火车站、港口和机场等外来人口密集地方设置传染病检测站,防止境外染病者进入,对于染病者采取强制隔离措施以降低接触率β; 3) 降低σ2使得R0<1. 致谢岭南师范学院攀峰计划项目对本文给予了资助,谨致谢意.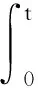

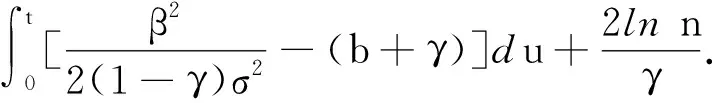
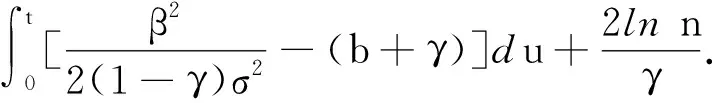
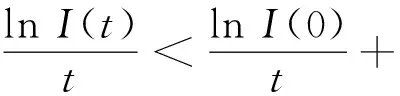

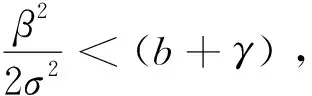
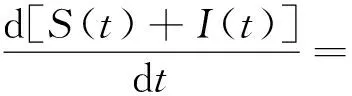
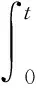
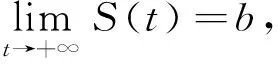
4 传染病在均值意义下的持久性
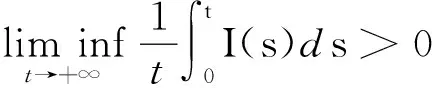
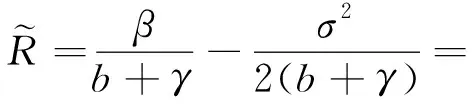
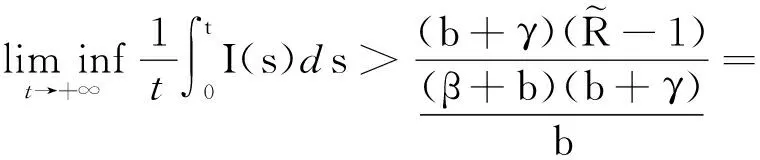
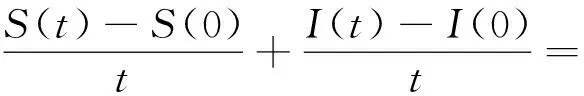
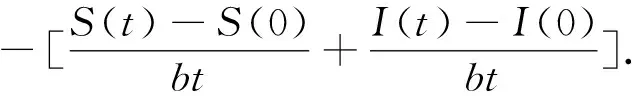
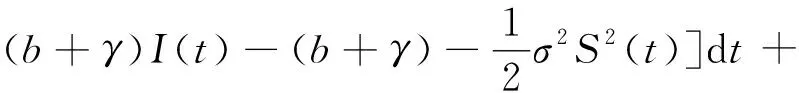
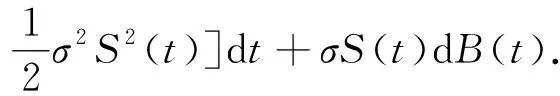
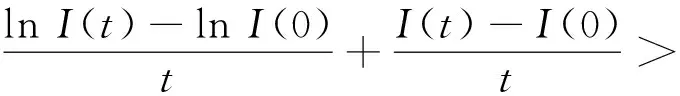
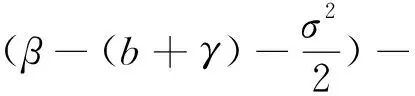
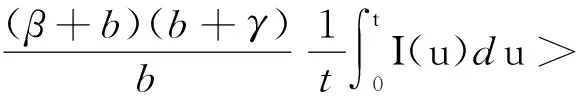
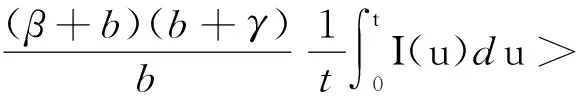
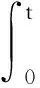
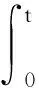
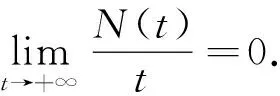
5 系统(5)生物学解释及防控措施
