基于响应面法全液压湿式驱动桥壳可靠性优化

周军超， 杜子学， 王 洁， 廖映华

(1. 四川理工学院 机械工程学院，四川 自贡 643000； 2. 重庆交通大学 轨道交通研究院，重庆 400074；3. 过程装备与控制工程四川省高校重点实验室，四川 自贡 643000)

0 引 言

全液压湿式驱动桥多应用在装载机等工程机械[1]。驱动桥壳作为全液压式驱动桥重要部件，主要作用是支撑并保护主减速器、差速器和半轴等，并支承车架及其以上各总成质量[2]。SHAO Yimin等[3]、刘为等[4]、GAO Jing等[5]、周军超等[6]和YU Xianzhong等[4]分别采用有限元方法对桥壳进行优化设计，对不同工况下桥壳的应力应变进行分析。郭冬青等[8]利用有限元分析技术对驱动桥试验模型和静力学进行了分析和优化。孙忠云等[9]基于静疲劳、静载荷、侧倾强度、紧急制动等条件约束，研究了某驱动桥可靠性优化模型，其结果表明优化效果明显。吕国坤等[10]提出基于二次响应曲面法进行优化设计，确定衬环为距桥壳片外端部时响应优化模型，通过对比桥壳改进前后的有限元分析得出加衬环后驱动桥壳应力明显降低，安全系数提高显著，并通过台架试验验证了改进措施的正确性和有效性。传统优化设计忽略了驱动桥结构参数的不确定性，其最优解只是数学意义的最优解，而实际工作时桥壳不但受到确定性因素影响，还受到诸如边界条件、尺寸波动等不确定性影响。因此对桥壳在确定性优化基础上进行可靠性优化具有重要意义。

响应面法(response surface methodology,RSM)在全局收敛性及优化效率上具有较强优势[11]，近年来已成为热门的优化方法。不少学者将响应面法应用到结构固有频率优化设计中[12]和应用响应面进行结构多目标分析与设计中[13]。比如：路怀华等[14-16]针对转向系结构参数不确定性，将可靠性与响应面结合，对汽车转向系统固有频率进行了优化。

笔者以全液压湿式驱动桥壳为优化目标，为提高驱动桥壳系统优化设计效率和可靠性，减少计算量，采用相应面方法和可靠性技术相结合对桥壳进行优化。首先建立驱动桥壳的有限元模型，通过有限元分析选择轮边板簧座附近，选取此处截面的形状作为优化目标函数，再进行拉丁试验设计，用二阶多项式获取桥壳的响应面近似优化模型，最后基于相应面模型进行驱动桥壳的可靠性优化设计，得到优化后桥壳的参数值与设计点。

1 桥壳有限元分析

笔者在CATIA中建立驱动桥桥壳模型，对有限模型进行处理。将图纸中出现的诸如倒角、圆角等细小特征尽量采取简化措施，最后桥壳模型如图1。将三维模型导入ANSYS软件后进行网格划分[6]，桥壳网格划分使用单元类型为SOLID185。该单元通过8个节点来定义，具有超弹性、应力刚化、蠕变、大变形和大应变能力等特点。有限元模型如下图2，共有331 201单元，166 923节点。

图1 桥壳模型Fig. 1 Axle housing model

图2 桥壳有限元模型Fig. 2 Finite element model of axle housing model

车桥模型单桥满载为7t，其整桥参数详见表1。

表1 车桥参数Table 1 Specific parameters of the axle

桥壳本体材料使用QT600-3，弹性模量为E=1.69×1011Pa，泊松比为μ=0.286。动载系数为3.5，安全系数为1.5。

对整体式桥壳进行满载不平路面行驶、车轮承受最大切向力、车轮承受最大侧向力等3种工况下的有限元分析，分析过程见文献[6]，分析结果如图3。从图3可看出：这3种工况下桥壳最大应力应变出现在轮边截面板簧座附近，选取此处截面形状作为优化目标函数。

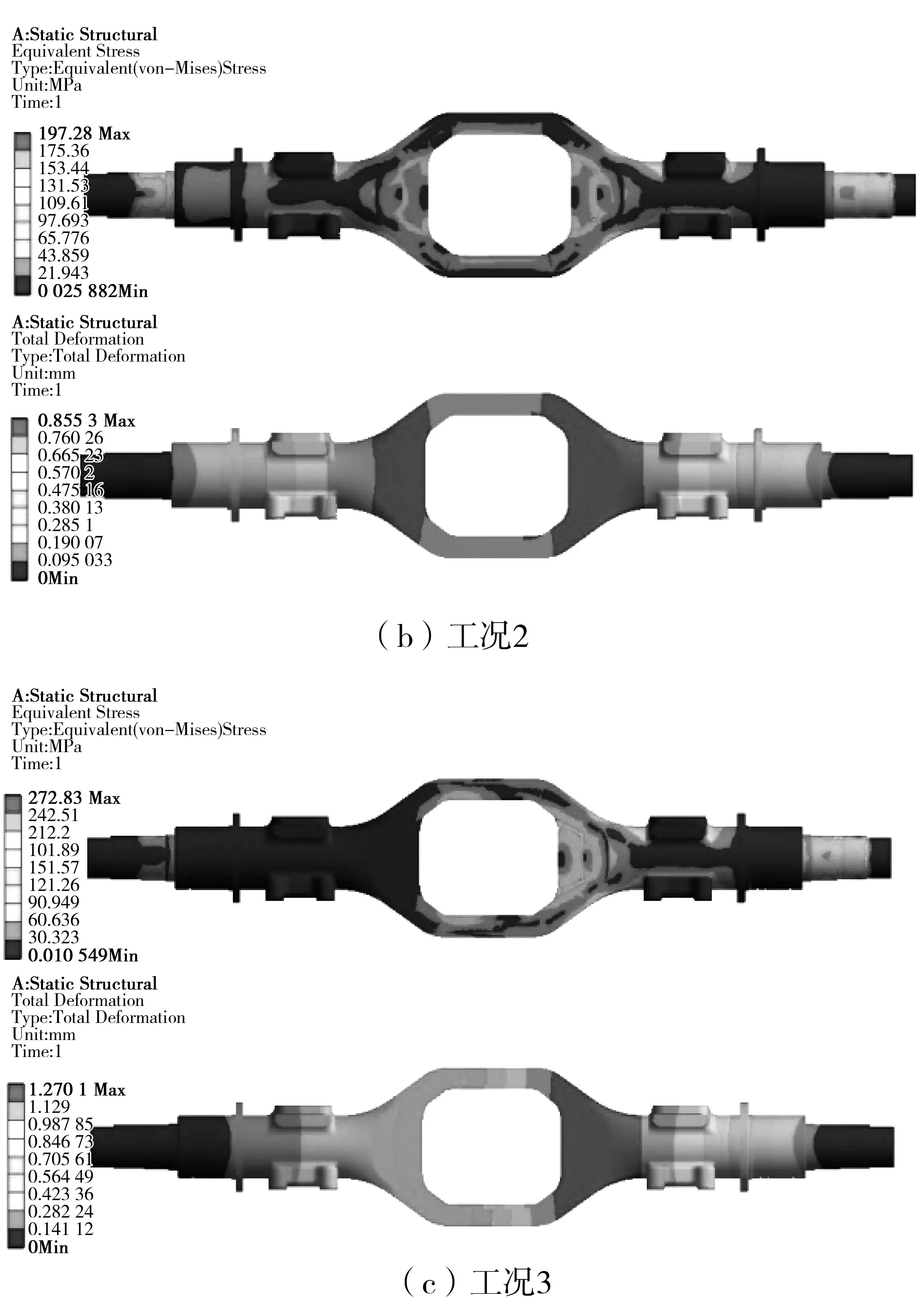
图3 3种工况下桥壳应力变形Fig. 3 Stress deformation of the axle housing under 3 working conditions

2 响应面法

响应面法基本原理是通过构造一个具有明确表达形式的多项式来表达隐式功能的函数[12]。用这个表达式代替实际函数进行复杂运算，因此可快速提高产品结构分析计算和优化设计。响应面法的在工程优化设计中，不仅可得到响应目标与设计变量之间的变化关系，而且可得到优化方案，即设计变量的最优组合，使目标函数达到最优。

假设系统响应Y与设计变量之间关系如式(1)：

(1)

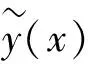
根据工程经验，响应面函数近似二项式表达式如式(2)[9]：

(2)

式中：β为未知系数；k为设计变量的数量；Y为预测响应值；β0为偏移项；βi为线性偏移；βii为二阶偏移系数；βij为交互作用系数。

3 驱动桥壳可靠性优化

可靠性设计原理是将设计变量(如载荷、应力等)视为一定分布规律的随机性变量，用概率方法进行产品可靠性设计[14]。可靠性设计是给定各个设计变量的概率分布函数，将各个确定的设计转化为概率约束。以确定性优化解为均值，取均方差与均值之比为0.01，采用基于响应面法可靠性优化计算。驱动桥壳可靠性优化数学模型如式(3)：

(3)

式中：F为响应面目标函数；P(t,X)为约束函数；R0为可靠度目标；hi(x)为约束条件。

当f(x)>0时，此时结构可靠度Rs如式(4)：

(4)

式中：f(x)为状态函数。

基于响应面法的汽车桥壳可靠性优化步骤如下：

步骤1：确定设计变量及设计目标。通过对驱动桥壳CAE分析可知，在不同工况下，钢板弹簧座附近受载情况最严重。选取该处整个截面作为优化变量。优化变量由宽度B，高度H和桥壳壁厚t这3个变量组成[9]。驱动桥最大应力至少为优化目标。

步骤2：构建响应面模型并验证模型的准确性。驱动桥壳优化目标和设计变量确定后，运用拉丁方试验设计方案，根据最小二乘法建立起桥壳目标函数的二次响应面近似模型。需对响应面模型进行精度验证分析，因此须对其近似值做F检验[17]。若符合工程要求的置信水平，模型是有效的，可利用该近似模型进行优化；反之，需要重新构建新的响应面模型。

步骤3：设定设计变量初始值。利用验证满足精度要求后的近似模型代替实际有限元模型进行分析时，需设定设计变量初始值。

步骤4：利用响应面进行约束函数和函数可靠性分析。首先利用函数面法构建约束函数，然后对约束函数进行可靠性分析。

步骤 5：利用遗传算法对步骤4的响应面模型进行分析，优化收敛则停止优化，获得优化结果。

步骤6：若步骤5无法满足最优解，则需要更新设计变量，回到步骤3，直到获得满意的优化结果。

基于响应面法桥壳可靠性优化流程见图4。

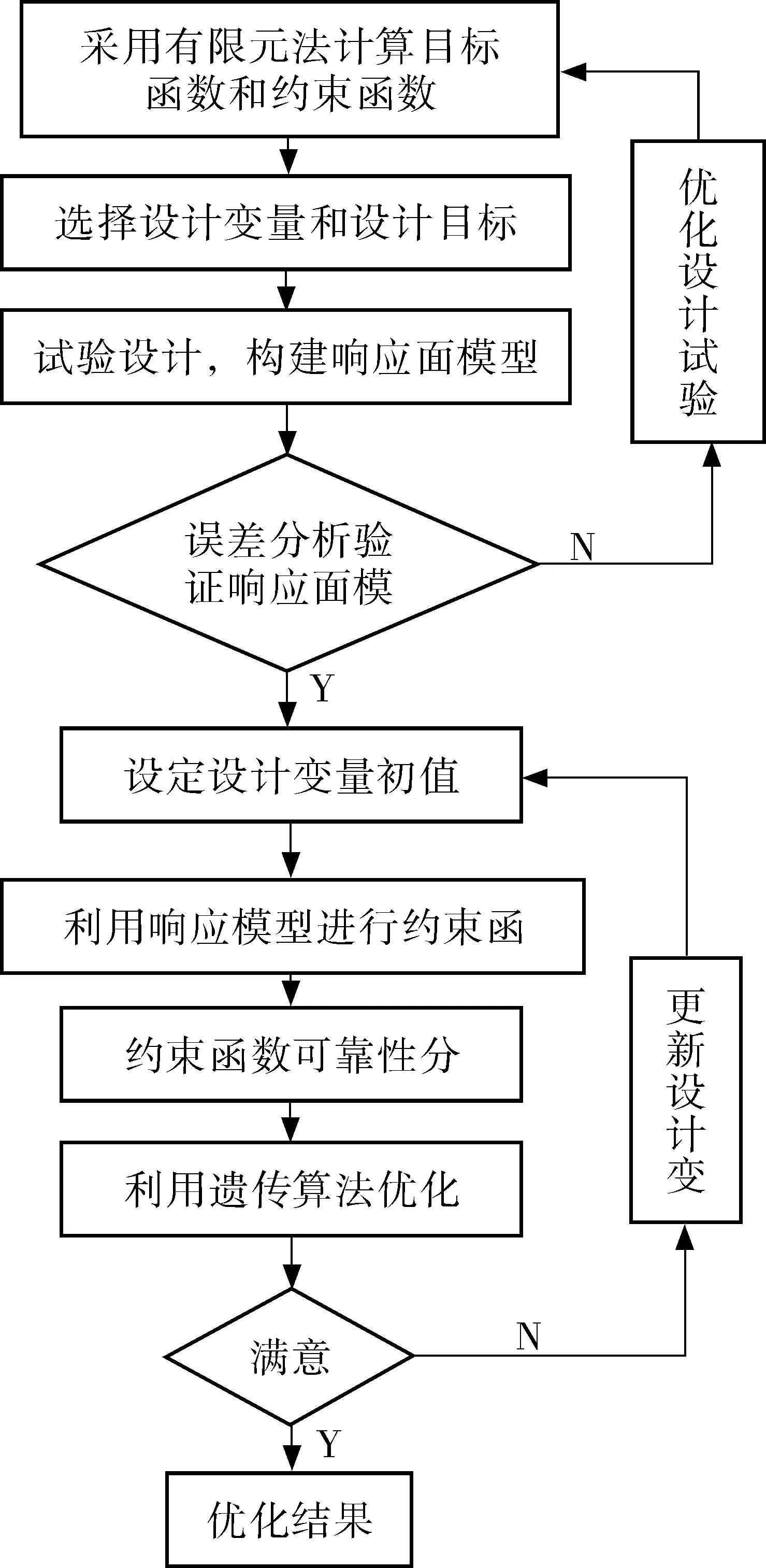
图4 基于响应面法的驱动桥壳可靠性优化流程Fig. 4 Reliability optimization process of drive axle housingbased on response surface method

4 实例分析

为减少试验次数，提高计算效率，笔者采用拉丁方程设计了15次试验，试验实际值和响应值如表2。以3种工况下数值仿真试验最大值作为原始数据点，由二次多项式构建的汽车桥壳响应面模型如式(5)：

(5)

式中：a1、a2、a3均为规范变量。

驱动桥壳结构优化前后结果如表3。由表3可知：优化后的桥壳最大应力降低了10.91%，桥壳质量降低了10.93%，桥壳可靠性提高了49%。对比文献[9]，在保证可靠性同时采取响应面优化具有良好的优化效率和收敛性。由于工程需要，将截面宽度由162.31 mm调整为162 mm，将高度由163.45 mm调整为163 mm，桥壳壁厚由9.78 mm调整为10 mm。

将修改后的优化变量值代入响应面可靠性模型，并与有限元模型进行分析对比，如表4。从表4可知：基于响应面模型预测值与有限元模型计算值相对误差在2%以内，优化结果具有较高的精度，基于响应面模型的优化结果满足设计要求。

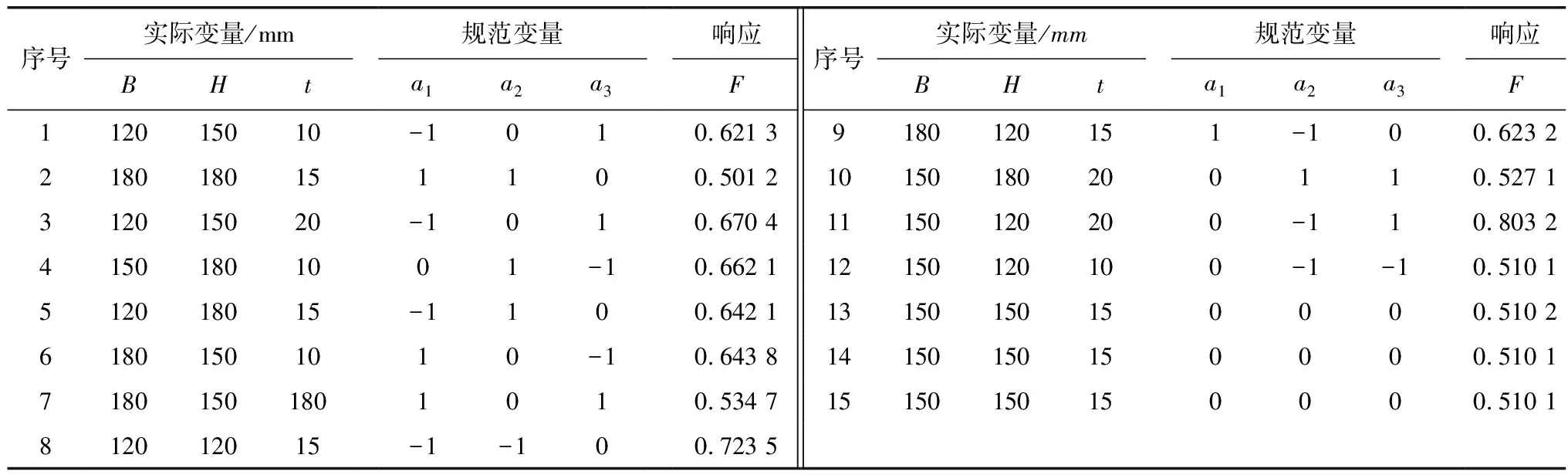
表2 实际值、编码值和相应数据Table 2 Actual value, code value, and corresponding data

表3 驱动桥壳结构优化结果对比Table 3 Comparison of optimization results of drive axle housing structure

表4 优化结果精度对比Table 4 Precision comparison of optimization results

5 结 语

笔者将优化分析与可靠性技术相结合，基于响应面法对桥壳结构参数进行了可靠性优化。并以某驱动桥壳为例，建立了桥壳有限元模型，通过有限元分析得到优化目标区域，结合拉丁试验设计构建了桥壳响应面近似模型。根据桥壳设计参数优化结果，优化后的桥壳最大应力降低了10.91%，桥壳质量降低了10.93%，满足相应强度要求条件能有效降低桥壳质量。与直接有限元模型相比，应用响应面近似模型能快速准确地获得最优值，且能有效解决工程优化时间长、效率低的问题，达到可靠性设计目的，为其他复杂结构优化设计提供借鉴。