基于响应面法的石质路基沥青路面结构优化研究

马士宾， 高建强， 魏建慧， 张晓云

(河北工业大学 土木与交通学院, 天津 300401)

0 引 言

我国是个多山的国家，现阶段，随着高速公路交通量越来越大，重载车辆越来越多，大量的高速公路需要在山区建设，所以不可避免的会采用石质路基的形式。在工程实际中既要充分发挥石质路基承载力强的特点，又要发挥路面结构层使用性能好的优势。为此在路面结构设计时应合理考虑石质路基的强度特性，确定与之相适应的路面结构，这就要求对石质路基路面结构的设计和施工的质量有更高的要求[1]。国外在对石质路基的路面结构设计方面的研究较少，一般对填石路基研究较多，如欧美国家对公路填石或填土石在内的材料作出了规定，但是对填石路基的路面结构研究较少。在国内，尚念宝[2]研究了石质路基条件下的沥青路面结构力学特征，研究发现随着路基模量的增大,路面结构所受最大剪应力也会增大，但所受的最大拉应力会减小，同时研究表明了在石质路基条件下柔性基层的路面结构更合理；郑琦[3]针对山区高速公路石质路堑段，详细地分析了界面条件的改变及超载对路面结构层内和层间应力应变的影响；郜玉兰等[4]分析了交通量及交通组成、交通荷载、长大纵坡、持续高温最不利组合和沥青混合料高温稳定性能不足等对重载交通下的山区高速公路车辙病害的影响，提出相应的车辙预防措施；王学勤[5]研究发现石质路堑段的沥青路面结构为复合式路面和半刚性基层沥青路面适宜用于重交通及特重交通等级路面，柔性基层沥青路面适宜用于中等交通及重交通等级路面；袁玉卿等[6]研究了石质路基路面的内力分布，结果表明路基模量变化对路面结构应力影响不大，路面结构层内一般只有压应力，随着深度增加逐渐产生拉应力，到达一定深度后逐渐趋于0。国内外对石质路基沥青路面结构的研究较少，都是基于材料性能、交通荷载进行研究的，忽略了路面结构组合优化设计。杨锡武等[7]通过建立离心模型研究了不同土石组成、不同容重、不同厚度的岩堆路基沉降变化规律和影响因素；贾学明等[8]采用测量面波速度的方法对土石混填路基进行了评价，结果表明，瑞利波法用于评价强夯施工效果高效、准确。基于以上研究，笔者将以沥青路面结构的各个结构层厚度为考虑因素，以沥青混合料疲劳开裂寿命、沥青混合料层永久变形量和路基竖向顶面压应变作为设计指标，采用响应面对石质路基沥青路面结构进行优化研究。

响应面法是一种简单而实用的优化方法，可以从多因素系统中找出最优条件的数学统计方法，是数学方法和统计方法结合的产物[9]。综上所述，笔者将依据山区公路路堑石质材料高回弹模量和承载能力强的性能，提出以级配碎石作为基层，建立以路面结构层厚度为响应因子，沥青混合料疲劳开裂寿命、沥青混合料层永久变形量和路基竖向顶面压应变作为优化指标的响应面优化模型。响应面法优化设计方法寻求到最合理的施工方案，最大程度降低了周期内投资成本。对石质路堑段沥青路面结构的施工具有现实意义。

1 原材料性能与路面结构组合设计

1.1 原材料参数

沥青采用90号A级沥青，粗集料采用4种级配粒径的石灰岩，其粒径范围为5～10、10～15、15～20和20～30 mm，细集料采用0～5 mm石灰岩，矿粉采用石灰岩矿粉。各材料性能如表1～表4，均满足规范要求。

表1 190 #沥青试验结果Table 1 190 # asphalt test results

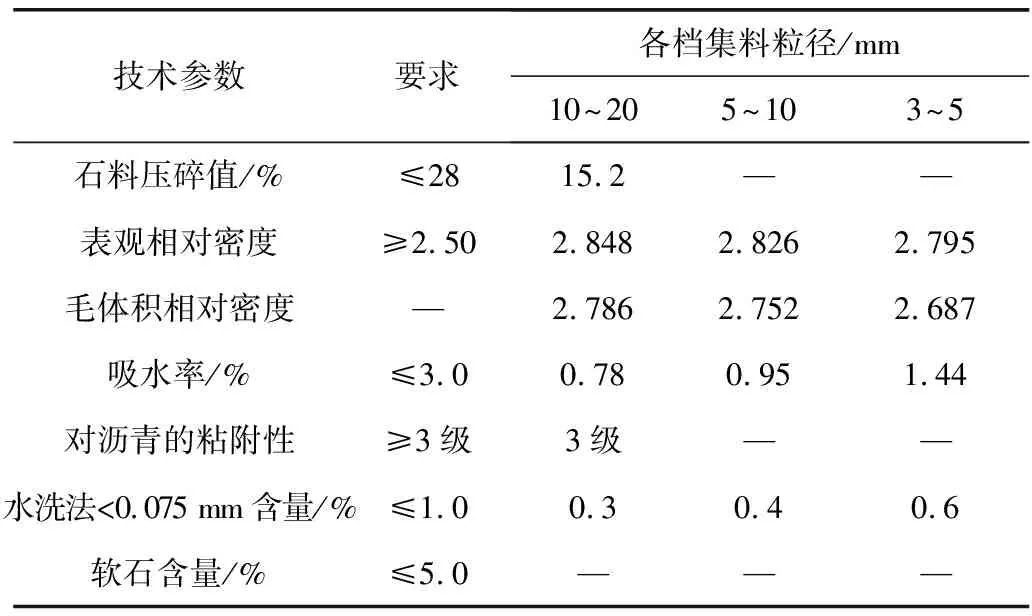
表2 粗集料技术性质Table 2 Technical properties of coarse aggregate

表3 细集料技术性质Table 3 Technical properties of fine aggregate

表4 矿粉技术性质Table 4 Technical properties of mineral powder

1.2 路面组合设计

笔者研究了石质路基沥青路面的结构层厚度对新规范指标的影响。在石质路基上加铺级配碎石作为基层，而各沥青面层的沥青混合料应满足JTG 050—2017《公路沥青路面设计规范》中的弹性模量和泊松比，在本文中上面层、中面层、下面层分别采用改性沥青AC-13、道路石油沥青AC-20、道路石油沥青AC-25。各个结构层具体参数如表5。

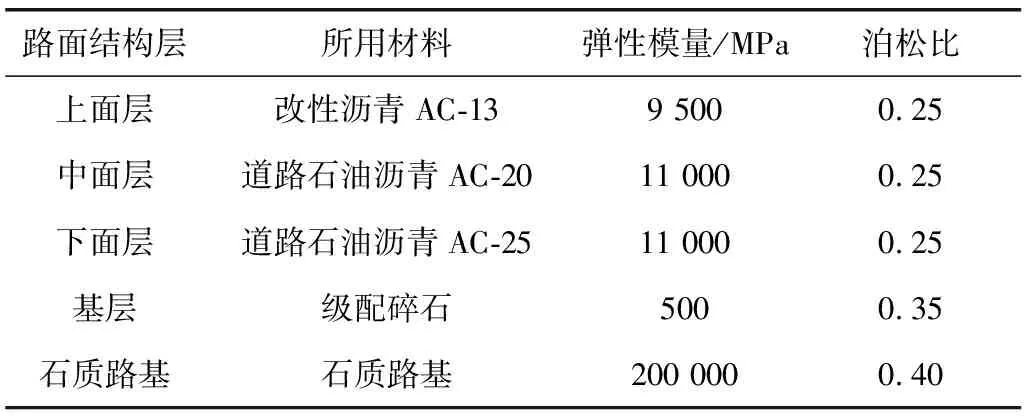
表5 路面结构层参数Table 5 Pavement structure layer parameters

为了能够充分研究路面结构层厚度对新规范规定的指标影响，笔者以各结构层的厚度为响应因素，沥青混合料疲劳开裂次数、沥青混合料永久变形量以及路基顶面竖向压应变为响应指标建立优化模型，进行评价。每个因素取3个水平进行分析，各参数如表6。

表6 中心组合设计各因素水平Table 6 Levels of various factors for central composite design cm

笔者通过对沥青路面结构层的上面层、中面层、下面层和基层厚度进行Box-Behnken中心组合设计，得到29组试验方案。应用kenpave软件计算出沥青层底拉应变、竖向压应力、路基顶面竖向压应变，并根据JTG 050—2017《公路沥青路面设计规范》计算得出29组试验方案的沥青混合料疲劳开裂次数、沥青混合料层永久变形量。具体数据如表7。

表7 Box-Behnken中心组合设计试验结果Table 7 Test results of Box-Behnken central composite design

2 响应面结果与分析

应用Design-Expert8.06软件对表7中的试验结果进行多元回归拟合，得到各个结构层厚度对疲劳开裂次数、永久变形量和竖向顶面压应变影响的回归方程如下。

永久变形量=19.1-1.3A+0.4B+0.9C-1.2D-6.5×

10-3AB-0.04AC+0.04AD-0.03BC+6.5×10-4BD+6.7×10-4CD+0.04A2-4.2×10-3B2-0.01C2+0.02D2

路基顶面竖向应变=2.0×10-4A-2.5×10-6B-3.1×10-6C-2.1×10-6D

疲劳开裂次数=1.1×108-5.9×108A-1.5×109B-9.2×108C+1.0×109D+9.9×107AB+5.6×107AC-4.0×107AD+5.9×107BC-3.8×106BD+0.06CD+3.0×107A2+5.0×107B2+2.8×107C2-1.8×107D2

响应面分析法中最重要的是对拟合得到的回归模型的方差和回归系数的显著性检验。永久变形回归的相关系数R2=0.948 9，F值为0.03；路基竖向顶面压应变的回归的相关系数R2=0.902 3，F值小于0.000 1；疲劳开裂寿命的相关系数R2=0.945 2，F值为0.004 8。因此该模型高度显著，能用此模型进行响应值进行预测。模型的方差分析如表8。

表8 二次回归模型的方差分析Table 8 Variance analysis of quadratic regression model

2.1 沥青层永久变形量

通过对表7中沥青永久变形量及4个因素(上面层厚度、中面层厚度、下面层厚度、基层厚度)应用Design-Expert8.06软件进行多元回归拟合，得到沥青层永久变形量回归系数显著性检验，见表9。

表9 永久变形二次模型回归系数显著性检验Table 9 Significance test of regression coefficient of permanentdeformation quadratic model

模型回归系数显著性的检验中，F值和P值反映了二次模型方程中每个回归系数的重要性。对于每个回归系数来说，其F值越大、P值越小，说明该回归系数越重要。由表9可见，A(上面层厚度)、B(中面层厚度)、C(下面层厚度)对永久变形量的线性效应显著，而D(基层厚度)影响不明显；AC、AD、BC对永久变形的交互影响显著,而AB、BD、CD的影响却很小；A2对永久变形的线性效应显著；而B2、C2、D2的影响小。

响应面是响应值对各实验因子所构成的三维空间曲面，从响应面分析图上可以形象地看出各因素对响应值的影响。图1、图2是根据各结构层厚度对沥青永久变形量所构成的响应面图形。图1是在下面层厚度和基层厚度一定的情况下，永久变形量随着上面层和中面层厚度变化而变化的趋势。图2是在上面层厚度和中面层厚度一定的情况下，永久变形量随着下面层厚度和基层厚度变化而变化的趋势。

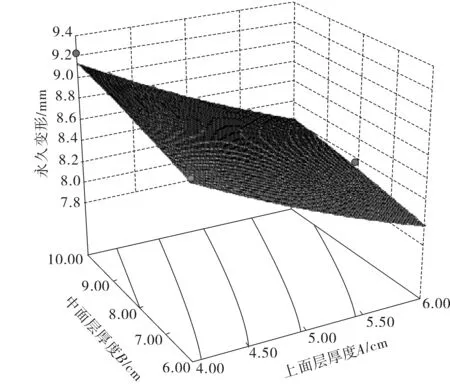
图1 沥青层永久变形与上面层、中面层图厚度之间的关系Fig. 1 Relationship between permanent deformation of asphalt andthickness of upper layer and middle layer

图2 沥青层永久变形与下面层、基层厚度之间的关系Fig. 2 Relationship between permanent deformation of andthickness of underlying layer and base layer

由图1可见，随着上面层厚度的增加永久变形量越来越小，而随着中面层厚度的增加永久变形量越来越大。

由图2可见，永久变形量随着下面层厚度的增加而增大，而随着基层厚度的增加，永久变形量呈现小幅度的先减小后增大的趋势。

2.2 路基顶面竖向压应变

通过对表7中路基顶面竖向压应变及4个因素(上面层厚度、中面层厚度、下面层厚度、基层厚度)应用Design-Expert8.06软件进行多元回归拟合，得到路基顶面竖向压应变回归系数显著性检验，见表10。

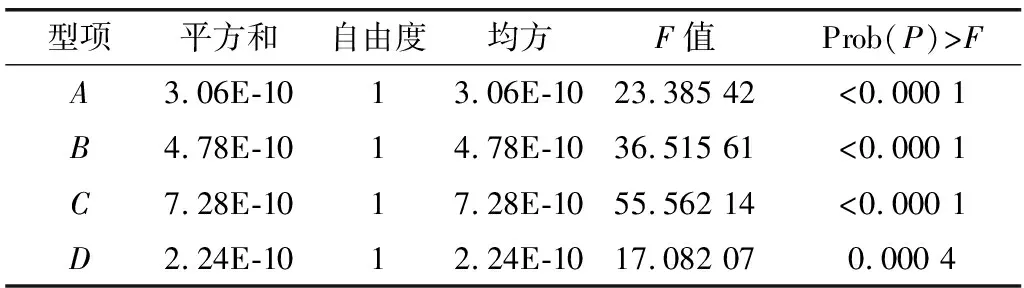
表10 路基顶面竖向压应变回归系数显著性检验Table 10 Significance test of vertical compressive strain regressioncoefficient on top surface of subgrade

由表10可见，A(上面层厚度)、B(中面层厚度)、C(下面层厚度)对路基竖向顶面压应变的线性效应显著，而D(基层厚度)的影响略微小一些，但是也很明显。

图3、图4是各个结构层厚度对路基顶面竖向压应变的影响的响应面图形。图3是在下面层厚度和基层厚度一定的情况下，路基顶面竖向压应变随着上面层和中面层厚度变化而变化的趋势。图4是在上面层厚度和中面层厚度一定的情况下，路基顶面竖向压应变随着下面层厚度和基层厚度变化而变化的趋势。

图3 路基顶面竖向压应变与上面层、中面层图厚度之间的关系Fig. 3 Relationship between vertical compressive strain on top surface of subgrade and thickness of top layer and middle layer

图4 路基顶面竖向压应变与下面层、基层厚度之间的关系Fig. 4 Relationship between vertical compressive strain on top surface of subgrade and thickness of underlying layer and base layer

由图3可见，随着上面层厚度和中面层厚度的增加路基顶面竖向压应变越来越小。

由图4可见随着下面层厚度和基层厚度的增加路基顶面竖向压应变越来越小，下面层厚度影响显著。

通过比较图3和图4也可以看出，基层厚度和下面层厚度对竖向顶面压应变的影响比上面层和中面层的影响显著。

2.3 疲劳开裂次数

通过对表7中疲劳开裂次数及4个因素(上面层厚度、中面层厚度、下面层厚度、基层厚度)应用Design-Expert8.06软件进行多元回归拟合，得到疲劳开裂次数回归系数显著性检验，见表11。

表11 疲劳开裂次数回归系数显著性检验Table 11 Significance test of regression coefficient of the number offatigue cracking

由表11可见，A(上面层厚度)、B(中面层厚度)、C(下面层厚度)对疲劳开裂次数的影响显著，而D(基层厚度)的影响不显著；AB、AC、AD、BC对疲劳开裂次数的影响显著,而BD、CD的影响却很小；A2、B2、C2对疲劳开裂次数的线性效应显著；而D2的影响效果显著性较小。

图5、图6是各个结构层厚度对疲劳开裂次数的二次响应面图形。图5是在下面层厚度和基层厚度一定的情况下，疲劳开裂次数随着上面层和中面层厚度变化而变化的趋势。图6是在上面层厚度和中面层厚度一定的情况下，疲劳开裂次数随着下面层厚度和基层厚度变化而变化的趋势。

图5 疲劳开裂次数与下面层、基层厚度之间的关系Fig. 5 Relationship between the number of fatigue cracking and thickness of underlying layer and base layer

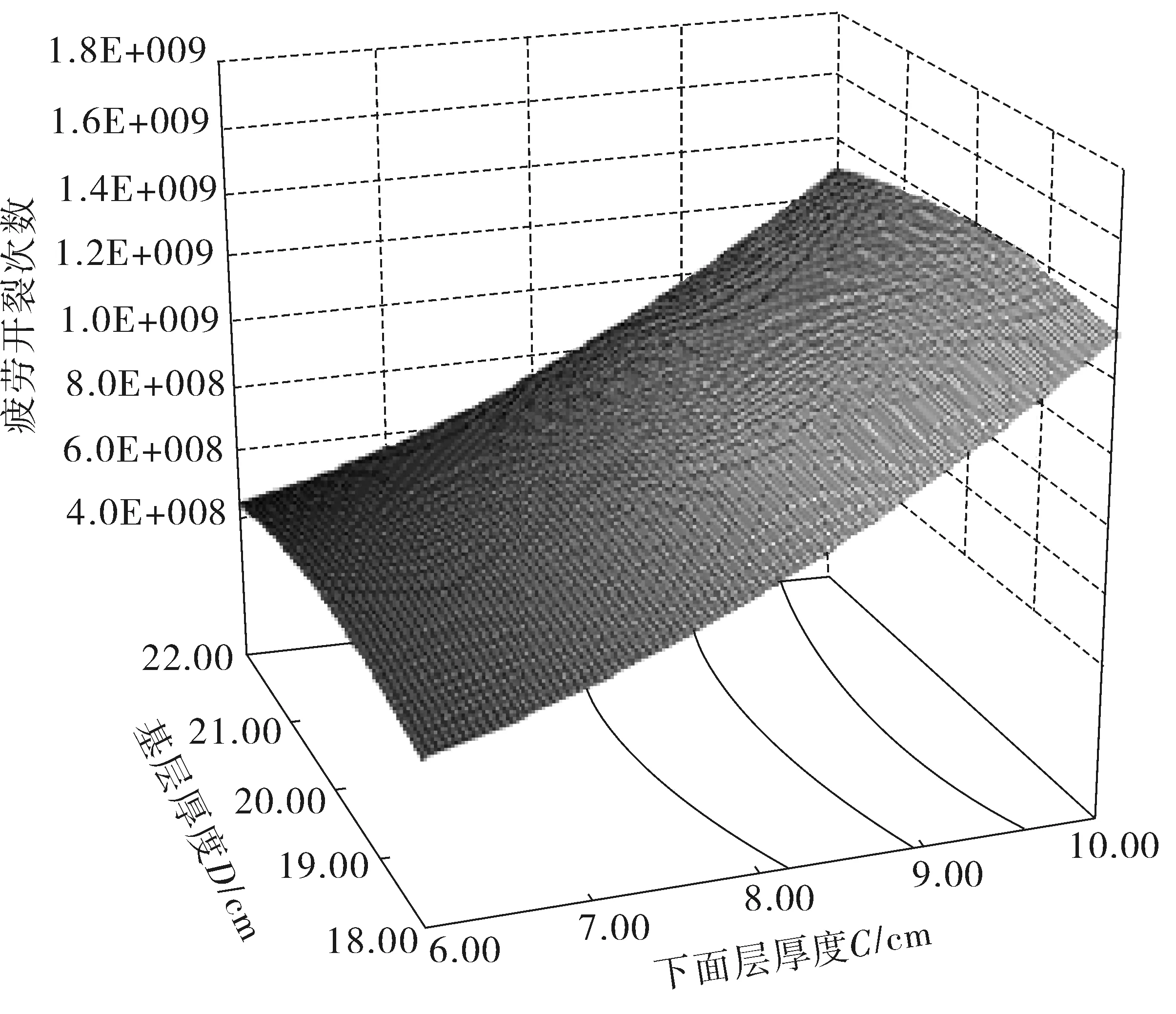
图6 疲劳开裂次数与上面层、中面层厚度之间的关系Fig. 6 Relationship between the number of fatigue cracking and thickness of upper layer and middle layer

由图5可见，随着上面层厚度和中面层厚度的增加，疲劳开裂次数呈现二次曲面递增的趋势，而上面层厚度的影响较为显著，对疲劳开裂次数影响的贡献大。

由图6可见，随着下面层厚度的增加疲劳开裂次数越来越多，而随着基层厚度的增加疲劳开裂次数呈现先增加后减小的趋势。而下面层厚度影响明显比基层厚度的影响显著。

3 结 论

笔者依据公路石质路基材料高回弹模量特点，应用响应面法对石质路基以及级配碎石为基层的路面结构进行优化设计，以路面各结构层厚度为响应因子，沥青混合料疲劳开裂寿命、沥青混合料层永久变形量和路基竖向顶面压应变作为优化指标建立响应面优化模型。通过实例对石质路堑段路面结构进行力学分析、优化设计，说明了在石质路基以及级配碎石为基层的条件下，各结构层厚度对这3个指标的影响。研究结论如下：

1)路面结构层厚度对永久变形量影响较大，随着中面层和下面层的厚度增加路面结构的永久变形量增加，下面层厚度的影响更为明显。而随着上面层厚度和基层厚度的增加永久变形量减小，基层厚度的影响较小。

2)路基顶面竖向压应变随着面层和基层厚度的增加而减小，下面层的影响最为显著，基层厚度的影响较小。

3)面层厚度对路面结构的疲劳开裂次数有显著影响，随着各个结构层厚度的增加疲劳开裂次数有较大的增加，而基层厚度的增加对疲劳开裂次数影响较小，当基层厚度在20 cm时，疲劳开裂次数最佳，当增加或者减少厚度时，疲劳开裂次数都有小幅度的减小。