徐振民管弦乐作品和声形态分析(下)

邱 月

(南京审计大学艺术教育部，江苏 南京 211815)

(二)纯四(五)度音程构成和声序进

在徐振民的管弦乐作品中，低音声部经常进行平行四、五度进行，以追求和声进行的色彩性，如《边寨音画》的主题乐句中的低音和声声部，构成了连续平行四(五)度和弦构成的和声进行。(见谱例8第5-7小节低音声部)

平行进行可营造出色彩感和流动感，满足印象主义音乐所追求的形象及其瞬间变化，所以，持续的平行和声进行成为印象主义作曲家经常使用的手法之一。“就平行进行而言，德彪西常保持平行和弦的结构一致性；拉威尔则比较自由，常在结构基本一致的和弦中夹置不同结构的和弦，仅保持和弦整体运动方向的一致。”[1]

此外，在《枫桥夜泊》第66-79小节，这是钟声之后的两个合头式乐句结构，从和弦构成音来看，都是以纯四(五)度音程构成和弦序进的，依次统计如下：

表格17

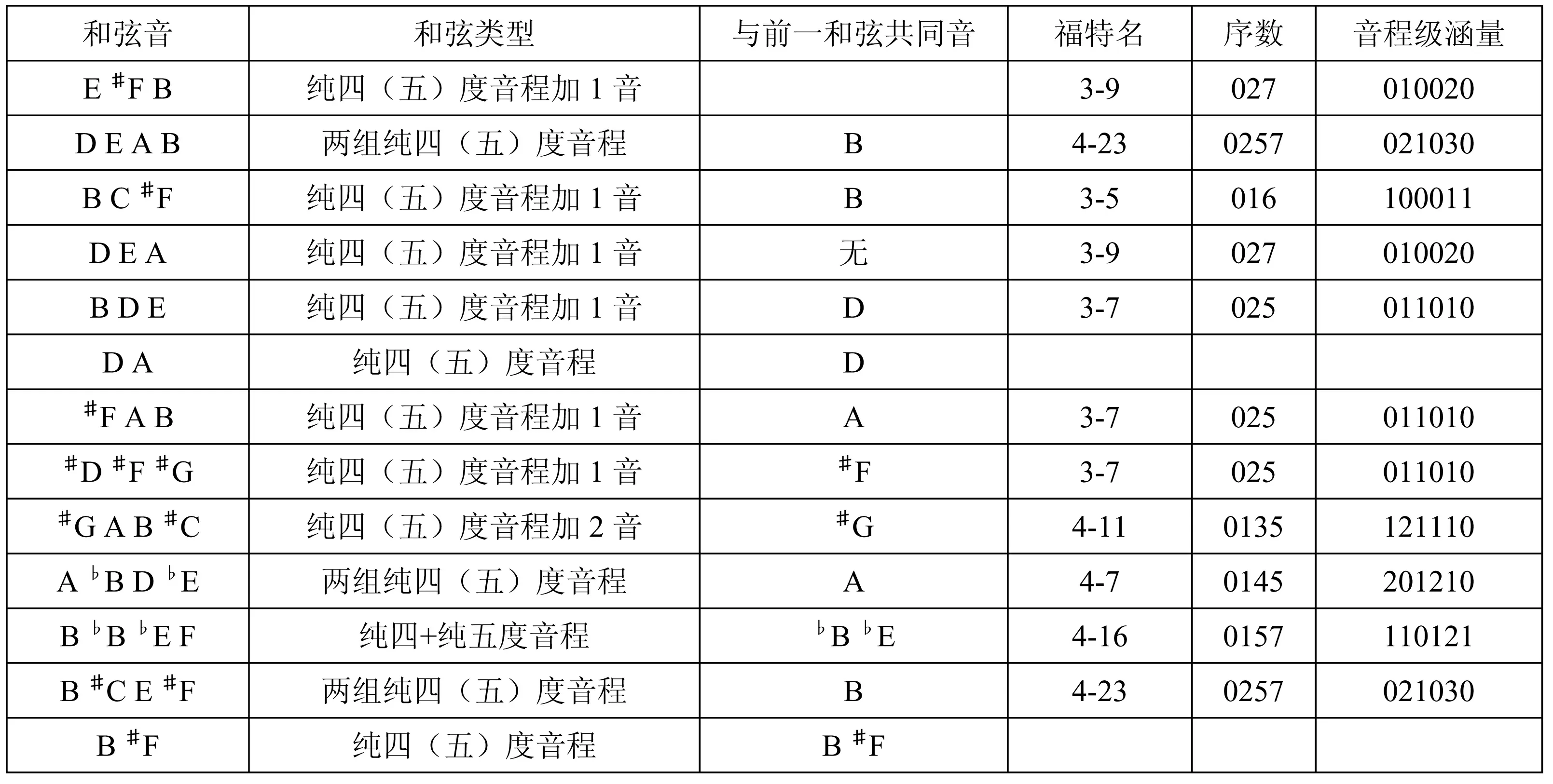
这一片段的和弦构成都是在纯四(五)度基础上形成的和弦音，通过音程级涵量可以清楚发现，只有表示纯四(五)度音程的音程级5位置上都有不同数量的表示，其他音程级都不相同，体现了纯四(五)度音程的多样化组合方式；在横向和声序进过程中，与上一和弦大多保持数目为1个共同音转换，追求统一性。

(三)高叠和弦构成和声序进

在徐振民管弦乐作品中，以高叠和弦为共同音形成和声序进，主要有两种形式，一种为高叠和弦不断重复，另一种为高叠和弦为共同和弦，形成和声序进。

1.高叠和弦重复(以“钟声和弦”为例)

表格18

钟声和弦重复六记，每小节一记，共六小节。并作为背景音持续整个第二段落。这个高叠和弦是在属九和弦的基础上加入三个音，这三个附加音都为不和谐音(见谱例5)。这种持续的和声进行手法在印象派大师拉威尔的作品中就有所体现，在其《小提琴与钢琴奏鸣曲》第二乐章的开始部分，小提琴连续8次奏出G大三和弦，达到强化和弦的目的。

2.高叠和弦为共同音

另外一种情况是以高叠和弦作为共同音，改变附加音，形成和声序进，这种手法在《枫桥夜泊》的“乌啼和弦”中有所体现：

表格19

乌啼和弦主要为两个高叠和弦的序进，这两个和弦都为十一加音和弦，略有区别的是附加音为加1音和加2音，附加音都为不和谐音，和弦音是在原有的和谐高叠和弦基础之上，加入不协和的附加音的手法来构建的，以此增加和弦的复杂性和听觉上的不协和度。

三、和声的音高集合张力

通过前文对和弦的类型以及和弦序进两个方面的分析，可以清晰了解徐振民管弦乐作品中主要使用的和弦以及序进过程中的组织关系。通过运用艾伦·福特的音级集合理论，可以从音程级涵量方面反映出不同音程级数量发生的变化，但变化并没有具体的数值表示。为了更加清晰明了地说明徐振民在作品中和声张力的布局手法，笔者希望通过对和弦的音高集合张力值的测算，更加直观地反映出张力的变化。本节采用的计算测量方法，是参考高为杰在《和声力学研究》中的计算音高集合的和声张力值的方法，具体为：代表音高集合的最高格位值加音高集合的格总值与音高集合中音元素数量的商，如果根五度音程，就再减掉1，如果没有根五度音程，就不加也不减，最后的数值即为音高集合的和声张力值。

“具体拟定出的计算音高集合和声张力值的公式为：

其中T代表音高集合的和声张力值；In代表音高集合的最高格位值，为音高集合的格总值；n代表音高集合中音元素数量。

ST=T-R

R=1，当排列有根五度音程

R=0，当排列无五根五度音程

公式中ST代表音高集合音响实现时的具体和声张力值。”[2]

笔者根据这两个公式，对徐振民作品中有代表性的和弦序进进行张力值的测算和分析，意义在于希望通过量化的数值更加直观地观察作品中和弦张力值的布局手法，每个和弦音的序号与下方图示序号相对应，列表如下：

(一)变奏片段的张力布局

以《边寨音画》B段11个变奏的和声进行为例，具体测算出每个变奏中主要和弦的张力值，观察其张力值的变化：

表格20变奏1

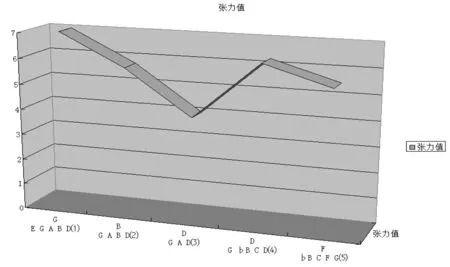
图1

由图表和表格可以清晰看出，变奏1中5个主要和弦，分别有五音、四音、三音组成，形成波浪式张力值变化。

表格21变奏2

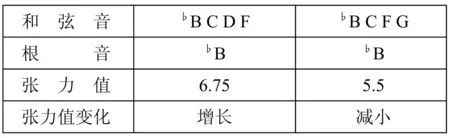
变奏2中两个和弦都为四音、根五度音程，张力数值在增长之后减小，继续保持波浪式前进的线条。

表格22变奏3

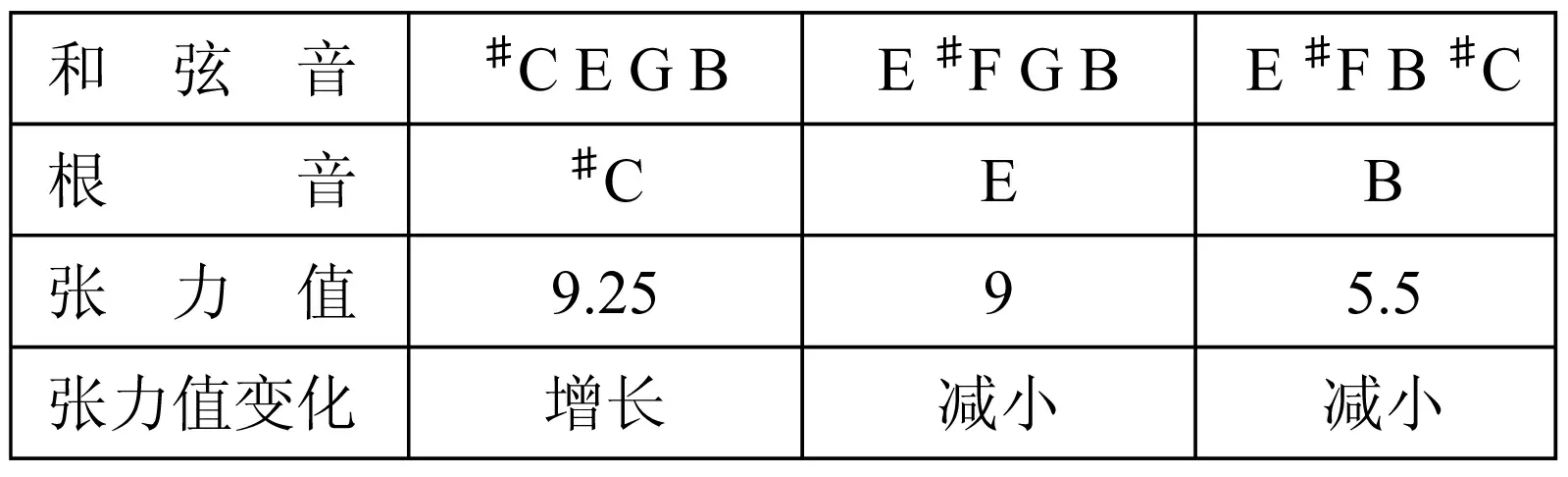
变奏3中三个和弦均为四音、有根五度音程，与变奏2保持一致，张力值在增加一次之后连续两次减小。

表格23变奏4

变奏4中两个和弦音为四音和六音、有根五度音，与变奏3形成对比，变奏3张力值后两次连续下降，而变奏4中连续两次上升，这是十一个变奏中第一次出现高叠和弦。

变奏5中的六个和弦为三音、四音交替、五音组成，根五度音程交替进行，张力值呈现典型波浪式行进轨迹。

表格24变奏5

表格25 变奏6

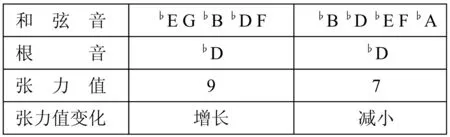
变奏6中两个和弦为四音、五音组成，前一个有根五度音程，后一个没有根五度音程，张力值下降。

表格26变奏7

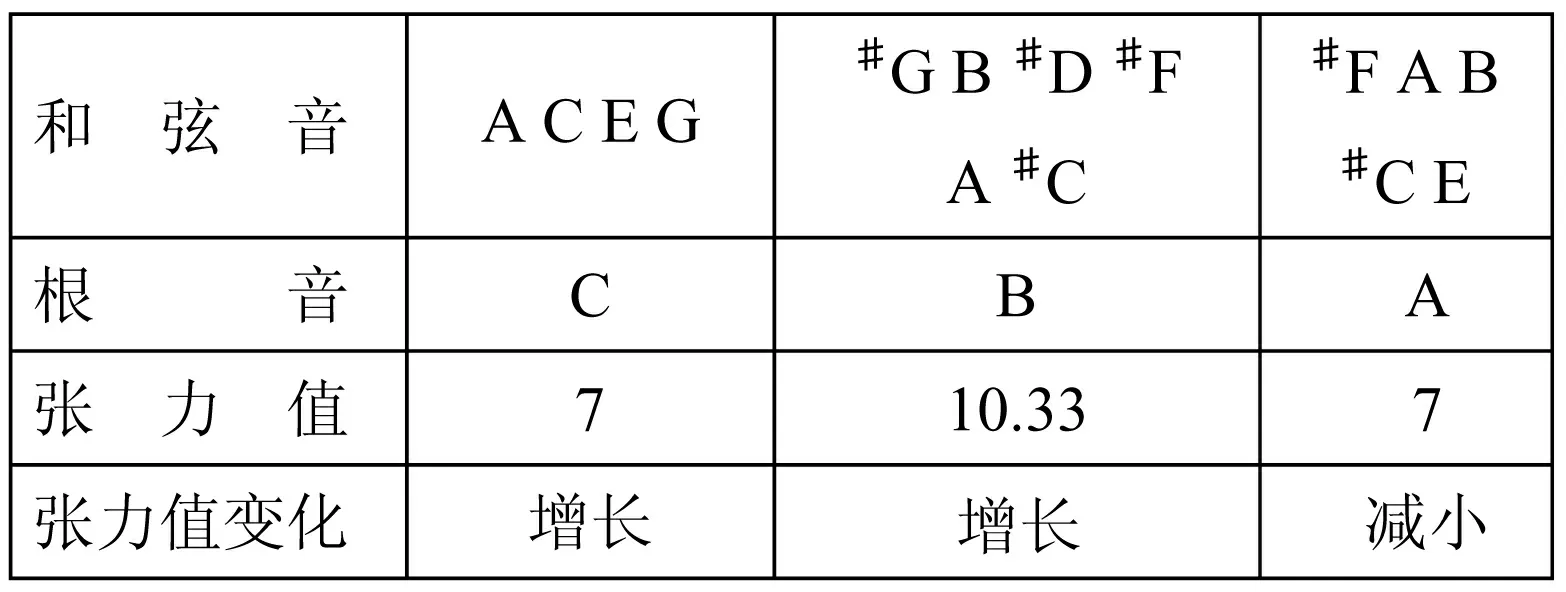
变奏7中三个和弦音，由四音、五音和六音组成，都有根五度音程，和声张力值在第二音达到最大。

表格27变奏8

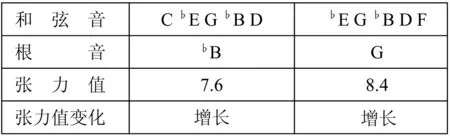
变奏8中两个和弦，均为五个音组成，第一个和弦无根五度音，第二个和弦有根五度和弦音，张力值增大。

表格28变奏9

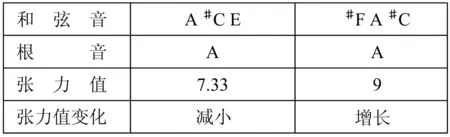
变奏9两个和弦均为三个音组成的和弦，第一个有根五度和弦音，第二个无根五度和弦音，第一个和弦与变奏8的结束和弦张力值相比，是下降之后再增长。

表格29变奏10

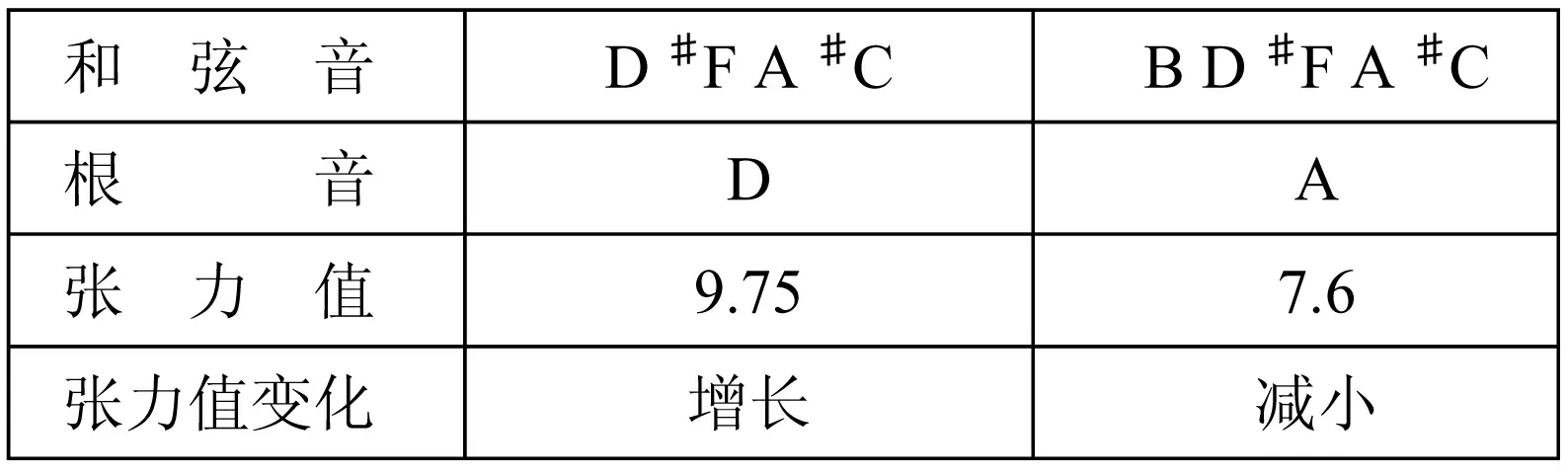
表格30 变奏11

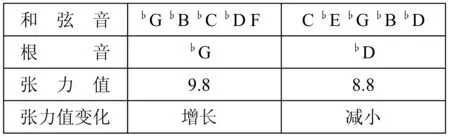
通过张力值汇总表，可以清晰发现徐振民在整个变奏片段的张力布局，十一个变奏的张力值呈波浪式前进，变奏1至变奏5的张力值呈螺旋式交替上升，变奏6张力值明显突强，明显高于前面五个变奏，在变奏7的位置张力值达到最大值10，变奏7刚好处于十一个变奏的0.636的位置，与黄金分割点0.618的位置极为靠近。从变奏7至变奏11，后五个变奏张力值也是呈螺旋式交替上升，但并没有超过变奏7，总体高于前六个变奏。从构成变奏的和弦数量来看，前六个变奏中和弦数量较之后六个变奏更多，但张力值较之后面六个变奏张力值较小，为了更好地研究这一段落中其他力度等影响和弦张力值的因素，见如下频谱分析图示：

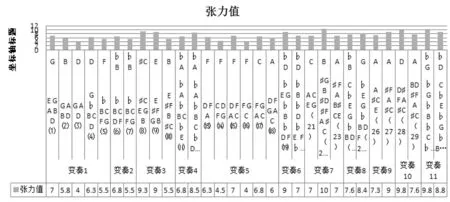
图2张力值汇总表

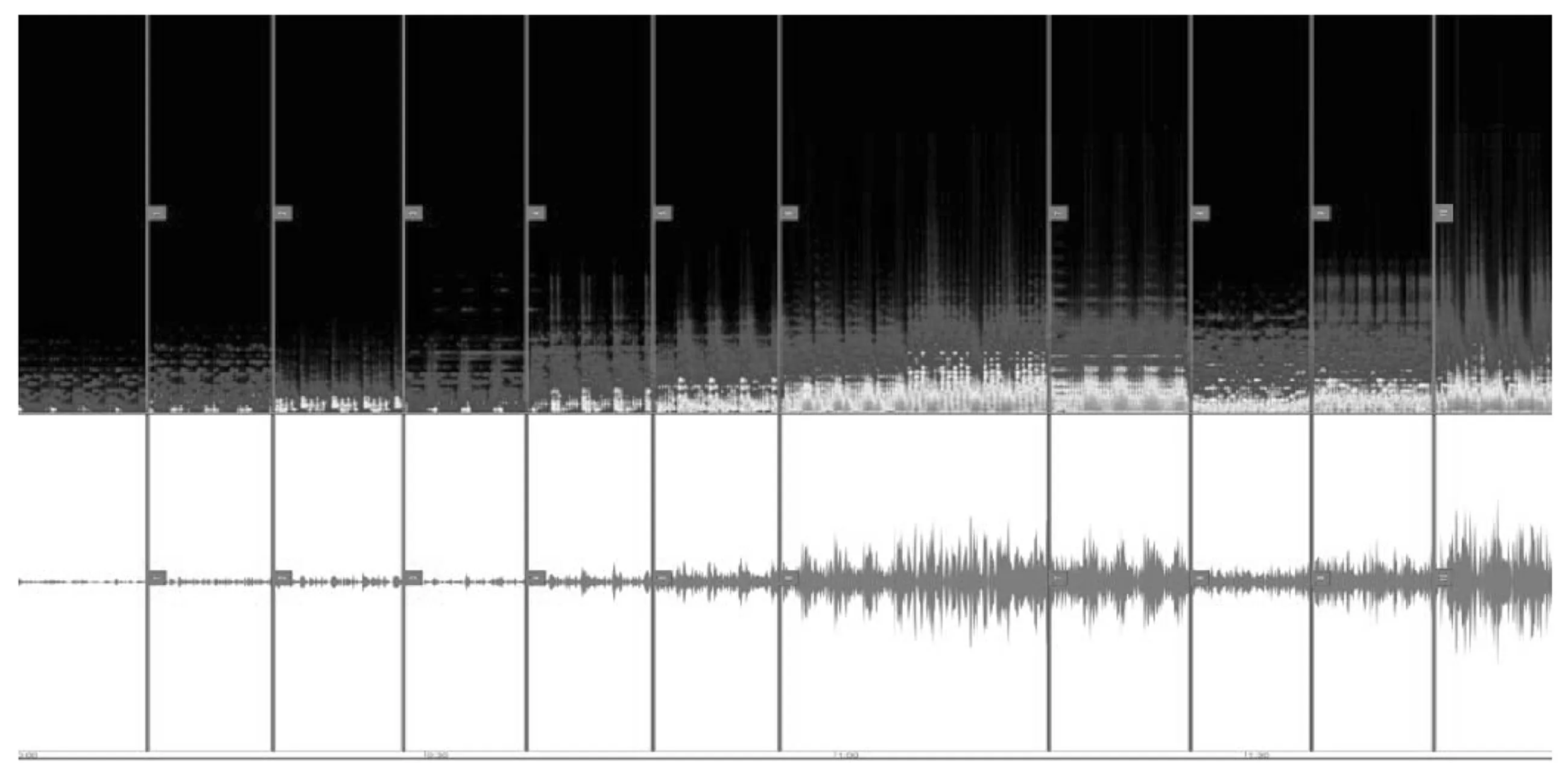
图3

这是用Eanalysis软件[注]Eanalysis是一个声音频谱分析软件，通常在分析电子音乐作品时使用，通过频谱谱面，可以反映音响的振幅、音色构成和频率分布等情况。对十一段变奏做出的频谱分析，结合张力值总体分布图来看，可以更清楚地观察音响的动态变化，最明显的是振幅和频率分布两个方面。

1.振幅层面：十一个变奏形成一个拱形结构，变奏1至变奏6振幅逐渐增大，在变奏7达到最高值，变奏7的和弦张力值也是最大的10，变奏8至变奏9逐渐递减，变奏11振幅继变奏7后出现第二次大振幅，和声张力值也是次高值9.8。

2.频率分布：与振幅同张力值布局相吻合的频率分布，在变奏7的频率分布范围最广，在变奏11达到了次广度。与振幅同和弦张力值的分布相得益彰。

(二)音乐形象的张力设计

1.钟声(见谱例4)

表格31

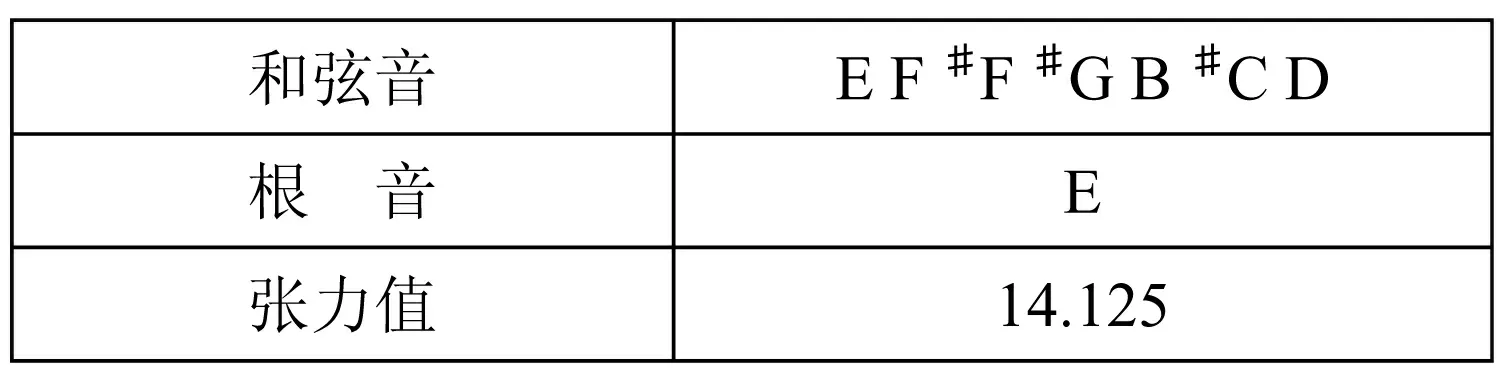
钟声形象的塑造仅用一个和弦，前6小节为六次和弦反复，在随后的第二段中，钟声作为背景一直贯穿于整个第二段，钟声和弦张力值为14.125，是《枫桥夜泊》中所有音乐形象中和声张力值最大的一个和弦。

2.乌啼(见谱例7)

表格32

乌啼的张力值是整个《枫桥夜泊》作品中张力值仅次于钟声的张力值，构成乌啼的两个和弦张力值都在13以上。

3.霜满天(见谱例11)

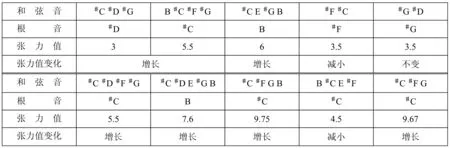
霜满天的音乐形象构成和弦中，张力值变化幅度极大，从3到9.67之间不断变化(表格33)，是音乐形象中张力变动幅度最大的。

4.江面(见谱例12)

表格33

表格34

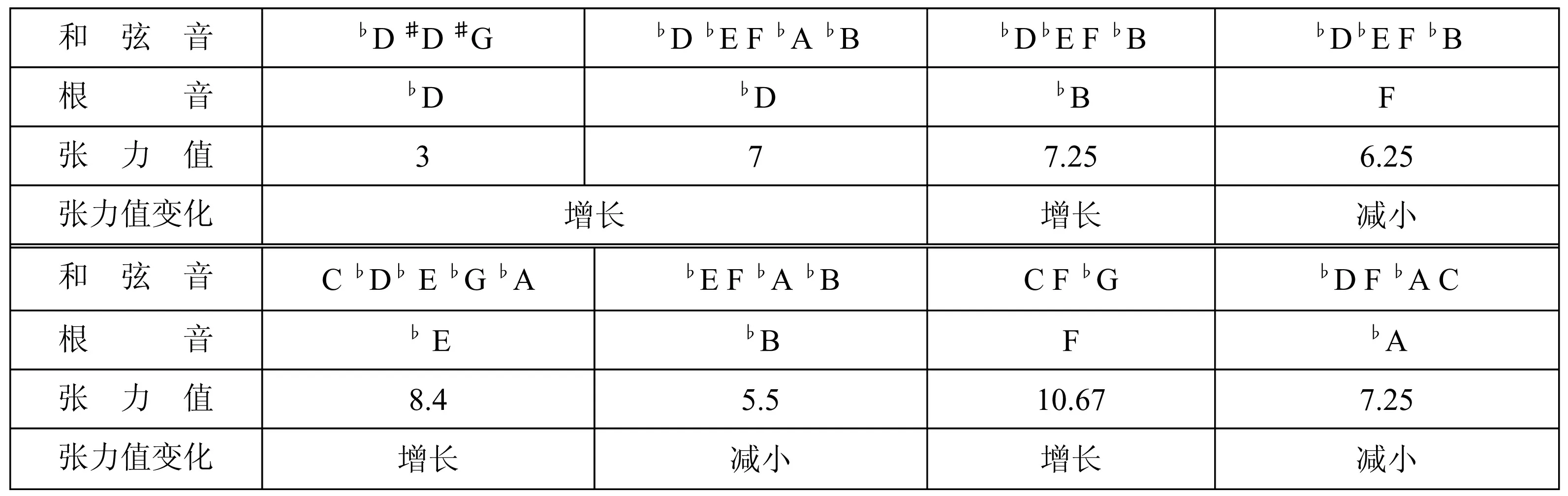
江面的张力值呈波浪式发展，张力值从3到10.67之间波动(表格34)，塑造江面的波动的动态形象。

综观四个音乐形象的和弦张力值变化，可以从张力值的数据角度准确反映出作者的张力布局，钟声形象为张力值最大，乌啼张力值次之，张力值最大的两个音乐形象用的和弦为一至两个，数量较少；在霜满天和江面的音乐形象中，和弦数量较多，张力值变化起伏较大。可见作者为了塑造音乐形象在和弦张力布局方面的技法。

结语

本文三部分内容的安排遵循层层递进的原则展开论述。第一部分为和弦的构成与设计。将徐振民先生管弦乐作品中的主要和弦进行归纳分类介绍。第二部分是从横向角度出发的和声序进分析，具体将由共同音、纯四(五)度音程、高叠和弦三种构成的横向和声序进进行了详细分析。在具体分析过程中，运用了艾伦·福特的音级集合理论，将各项参数用列表的形式做一梳理，可以直观地反映出各和弦音在进行过程中，音程级以及其他各项技术参数的变化。第三部分是在前两节的基础之上，对典型片段中的张力布局进行分析，为了更加直观地观察作曲家对核心片段的和声张力构建，这一部分对和声张力值的计算方法采用的是高为杰在《和声力学研究》中对和声张力效应量化分析的计算方法，此外还使用Eanalysis声音频谱分析软件，通过频谱谱面，可以反映音响的振幅、音色构成和频率分布等情况。这样通过和声张力数值以及声音频谱图对整个和声片段进行分析，通过数据可以更加直观地反映出徐振民先生在一些经典片段和表达音乐形象中的和声设计。