超冗余移动机械臂逆运动学快速求解的两种方法比较
2019-03-11马影陈丽高其远邓宇翔
马影 陈丽 高其远 邓宇翔

摘要:超冗余移动机械臂的逆运动学求解一直是机器人领域研究的热点,特别是逆运动学求解过程中导致的计算量大、机械臂的位形偏移量大及能耗大等问题还未得到有效解决。因此本文给出基于几何方法的超冗余机械臂逆运动学快速求解算法,并分析了两种关节位置更新策略的能耗。第一种关节位置更新策略为“关节落在连线上”,即更新后的关节位置落在该关节的目标点和与其相连的前一个关节的连线上;第二种关节位置更新策略为“关节落在轴线上”,即更新后的关节位置落在前一时刻的该关节和与其相连的前一个关节的轴线上。从运动过程中关节跟踪角度变化范围多少出发,比较超冗余移动机械臂在这2种关节更新策略下运动特点。实验结果显示,方法1具有关节移动范围小,移动距离短的特点。方法2具有各个关节都有相似的运动轨迹,机械臂的末端跟随效果好的特点。
关键词:超冗余移动机械臂;逆运动学;几何解析法;关节更新策略
0引言
超冗余移动机械臂是由杆件、关节、末端执行器组成的互相连接互相依赖的运动机构。相对于固定机械臂而言,超冗余移动机械臂具有作业范围大、灵活性高和广阔的应用前景。因此移动机械臂广泛应用在搬运、焊接、灾后救援、探测、等恶劣环境中。但是对于冗余型移动机械臂而言,逆运动学求解计算量大且不唯一、机械臂运动位形偏移量大、逆解求解速度缓慢等是需要攻克的难题。
近年来,求解机械臂逆解的方法主要有数值迭代法、智能算法。目前,也相继涌现出一系列的研究成果。朱经纬等人提出了一种自适应粒子群算法求解机械臂逆运动学,以正向运动学方程为基础,将冗余机械臂逆运动学解问题转化为等效最小值问题。张熙峰等人提出了基于遗传算法的机械臂逆运动学求解,将种群定义为机械臂的关节角轨迹层面。利用连续性函数来实现算法的初始化算子、交叉算子和变异算子。张云峰等人提出了基于改进QPSO-NN(粒子群优化)的冗余机械臂逆运动学算法,以冗余机械臂末端位姿为输入,利用神经网络算法求得其逆解。李梅红提出了一种动态变步长果绳算法求冗余机械臂逆运动学解,在果绳算法的基础上,通过适应度值对果绳种群进行动态规划,此后2个子群按照不同的公式进行搜索步长的计算并完成位置更新。上述智能算法能很好地求出逆解,但由于中间过程需要搜索、判断、寻优过程,因此计算量大,导致求解速度较慢。
本文提出了基于几何推导的解析算法,可以快速完成逆运动学的求解。根据杆的长度约束可以唯一地确定出关节移动后的具体位置。给出了2种关节更新策略:关节落在连杆上的方法(方法2)和关节落在连线上的方法(方法1),仿真分析了2种方法的各种特点。
1 超冗余移动机械臂结构和工作空间分析
1.1 结构参数介绍
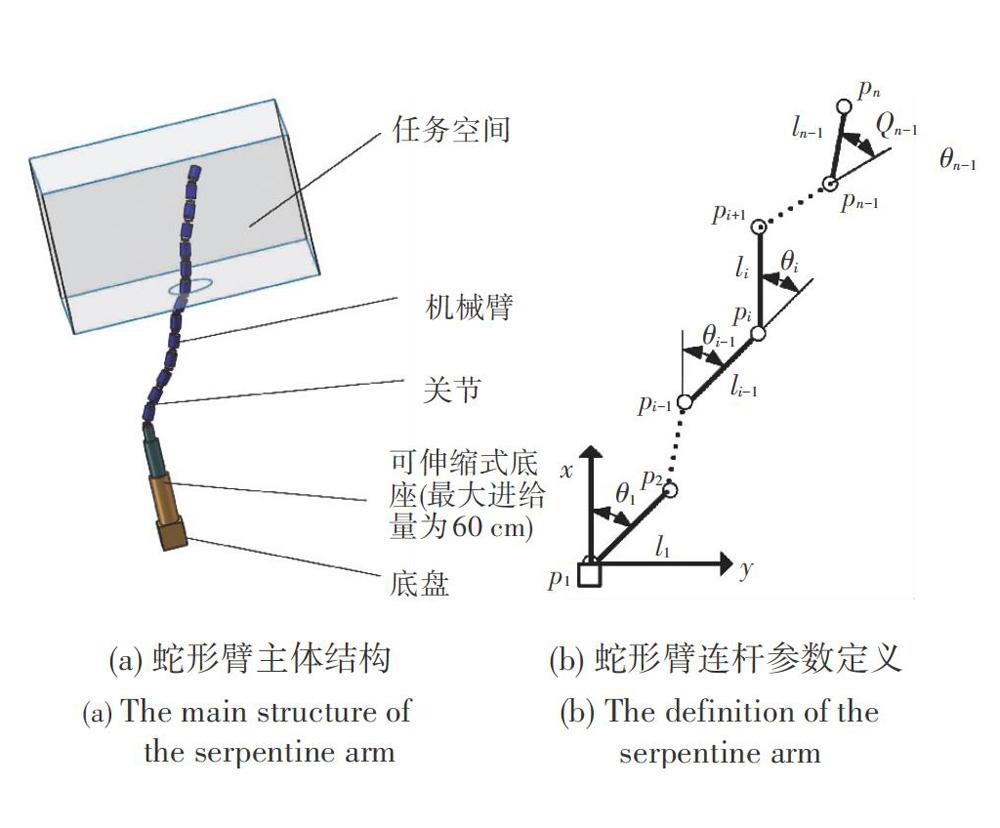
文中的超冗余移动机械臂主要由基座、臂杆、关节、末端执行器和驱动装置组成,整体结构如图1(a)所示。其中,基座装在可移动的平台或者直线导轨上,与移动基座固接的部分为可伸缩机构,可以实现基座竖直或水平方向上的移动。规定基座的最大进给距离为60cm,机械臂的连杆共9节,由10个关节相连,单模块由连杆和关节组成,长度为5cm,机械臂总长为80cm。机械臂的目标工作空间为lOOx100cm2的平面,具体连杆参数定义如图1(b)所示。
单模块参数定义如下:pi为模块i的关节位置,li为模块i的连杆长度,θi为模块i和前一模块i-1的相对转角。
1.2 末端执行器的可达空间分析
根据机械臂的长度和底座最大进给量,通过正运动学推导确定出末端执行器的运动区域。借助拉丁超立方抽样获得工作空间的采样点,拉丁超立方取样对样本数量的节省上效果尤为显著,适合冗余机械臂的工作空间分析。首先根据几何关系,推导各个关节位置关系如下:
xi=xi-1+li-1cosθi-1(1)
yi=yi-1+li-1cosθi-1
(2)
其中,pi-1(xi-1,yi-1),pi(xi,yi)分别表示模块i-1的前后两个关节的位置坐标,θi为连杆i和连杆i-1的相对转角,通过式(1)、(2)即可迭代求出末端执行器的平面位置。在关节角度运动范围内取样点个数为2000,图2给出末端执行器的可达运动区域。其规则有效区域约為lOOx40cm2的平面区域。
2 移动冗余机械臂末端跟随算法设计
本文提出的几何分析方法进行的运动学逆解就是根据机械臂的目标位置,把该目标点作为机械臂末端的更新位置。在满足连杆长度的前提下确定前一时刻关节更新位置。以此类推实现多个关节的位置更新。在该方法中所选择的关节更新策略不同,就会得到不同的运动轨迹。下面针对本文所采用2种跟踪方法设计实施步骤,拟展开研究详述如下。
2.1 方法1:关节在连线上更新策略
2.2 方法2:关节在轴线上的更新策略
3 原理分析及实验比较
3.1能耗计算
机械臂关节转动需要消耗关节电机的转动动能,同时机械臂连杆位置的改变需要克服自身重量的势能变化。因此机械臂运动过程所消耗的能量包括重力势能和转动动能。下面给出理论上机械臂运动的能量推导过程。如图6所示,图中h1、h2、h3分别对应机械臂的某一连杆的初始位置、方法2和方法1更新后位置的重心高度。
由于w1、w2,无法解析求解,需要调用数值模拟计算,通过实验数据来验证2种方法的能耗结果。
由于机械臂的运动为反复运动,整个过程中重力做功可以部分抵消,因此这里忽略重力做功。再者由于机械臂的各个关节的输出力矩是变化的,在没有进行动力学分析情况下,采用关节角度改变的多少间接衡量2种关节更新策略的优劣。其定义为。
3.2 实验仿真图
仿真为机械臂在同一平面内走出一个半径为8cm的圆,分别用上述2种关节更新方法展示执行效果。运动跟踪过程分10跟踪阶段完成。图7和图8给出轨迹跟踪过程中机械臂在每一阶段下的状态结果。
在只要求末端执行器跟踪目标轨迹的前提下。可以看出方法1的运动轨迹保证了末端关节直接接近目标,而其余关节的位置则脱离目标轨迹,缩短了非末端关节的中间移动距离。因此该方法达到总体上较短的跟踪路径:而方法2的运动轨迹各个关节更接近于实际轨迹,前端关节趋向于跟随末端关节的运动,机械臂的运动轨迹更光滑,机械臂各个关节相对于前一关节的相对转角变化不大,机械臂整体的位置的移动距离变大。
方法1的能量消耗变化详见图9.从图9(a)可以看出,随着关节号的增加(关节1与基座相连,关节10为末端),关节转动的角度位置显著增加,距离基座越近,关节运动范围越小。从图9(b)可以看出,关节转动角度大小随向前的运动距离增加而增加(stepl为第一阶段,stepll为跟踪的最后阶段)。通过公式(13)计算,在运行整个轨迹后,机械臂的各个关节总的关节转动范围为4.1285rad。
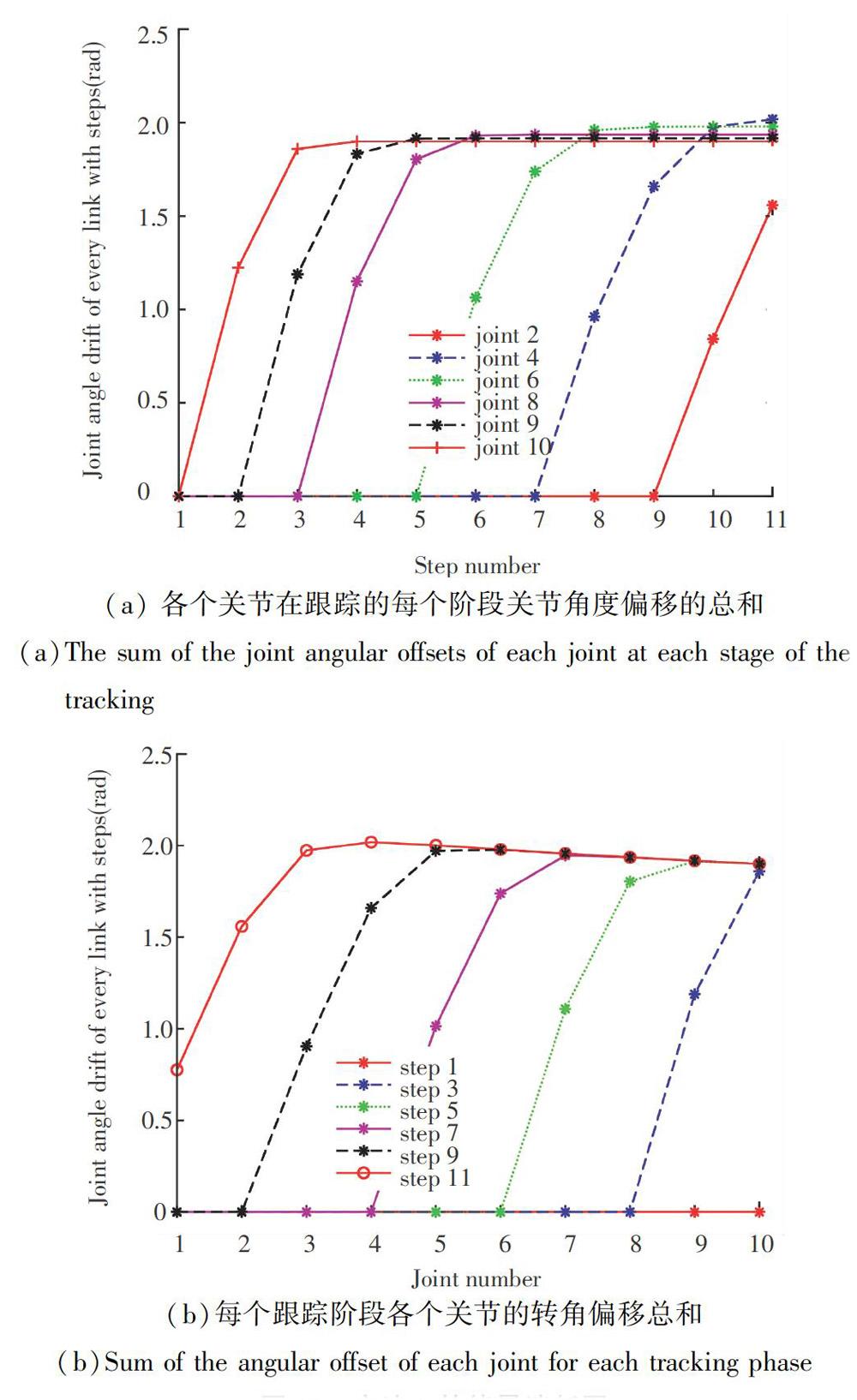
同时,研究又得到方法2的能量消耗变化详见图10.从图10(a)可以看出,随着关节号的增加,关节转动的角度位置显著增加,在跟踪最初阶段距离基座越近,关节只有移动没有转动,例如关节2是在第9步开始转动运动,关节4是在第7步开始转动运动。当跟踪到稳定阶段,各个关节达到相同的运动范围。从图10(b)可以看出,每条线表示运动到该步后,各个关节总的转动范围。关节转动角度大小随向前的运动距离增加而增加。在第11步,各个关节的运动范围达到最大。通过公式(13)计算,在运行整个轨迹后,机械臂的各个关节总的关节转动范围为18rad。相比方法1.方法2的关节总的移动范围增加。
比较图9(a)和图10(a)可以看出,采用方法1在跟踪的每一阶段,各个关节都在运动,距离基座近的关节运动幅度小。采用方法2时,初始是部分关节转动,距离基座近的关节只有平移。当跟踪到稳定阶段,各个关节达到相同的运动范围。可以看出各个关节的末端跟随的效应。比较图9(b)和图10(b)的同一运动阶段具有可比性,例如在共同跟踪最后阶段的stepll可以看出,方法l的各个关节角度移动范围依次减小,而方法2的各个关节角度移动范围基本相等。
综上所述,可知方法1具有关节移动范围小,移动距离短的特点。方法2各个关节都具有相似的运动轨迹,其末端跟随效果更好。
4 结束语
本文给出基于几何方法的超冗余机械臂逆运动学快速求解算法,并分析了2种关节位置更新策略的能耗。在本研究中,方法1为“关节在连线上”,方法2为“关节在轴线上”。通过控制末端跟随同一目标运动。从能耗和运动平稳性两个角度来比较2种几何方法的优劣。在此基础上,进一步分析后可知,2种方法都可以實现超冗余度机器人逆运动学的快速求解,实际应用中可根据任务要求选择相应的关节更新策略。
