基于有限体积法Godunov格式的水锤计算模型
2019-03-11刘德有张永会王家泽潘天文
赵 越,周 领,刘德有,张永会,王家泽,曹 云,潘天文
(1.河海大学水利水电学院,江苏 南京 210098; 2.国网新源控股有限公司白山抽水蓄能电站,吉林 吉林 132013)
在有压管道系统中水力元件(如阀门、泵等)启闭或启停可能会产生危险的水锤现象,从而可能对管道产生破坏甚至造成人员伤亡等严重的事故,因此,水锤问题的计算分析对于管道系统的设计以及安全运行至关重要。特征线法(method of characteristics,MOC)具有简单、准确的特点,在解决管道瞬变流问题时被广泛应用。然而,实际工程中的管道系统常会出现不同材质的管段或支管(不同波速)、短管等问题,在采用固定网格的特征线法进行计算分析时可能需要通过改变波速或者网格长度来满足库朗特数条件,这就使得计算变得复杂而且可能引起较大的计算误差。
近年来,有限体积法广泛用于气体动力学和浅水方程问题的模拟。在保证质量和能量守恒条件下,有限体积法对于不连续问题可提供合理的求解方案,并可有效避免虚假振荡。Guinot[1]将有限体积法应用到水锤问题,得到了类似于带内插特征线法的一阶格式;余代广等[2]为提高水锤计算精度,采用特征线法对摩阻项积分得到非恒定摩阻模型;Zhao等[3]在基于Godunov格式对水锤问题进行模拟时,应用Riemann求解器进行求解从而得到了一阶和二阶的格式;耿艳芬等[4-6]采用特征分解的格式构造出一阶和二阶的Godunov格式对水锤问题和浅水方程进行了分析,并基于无结构网格单元中心有限体积法对二维对流扩散方程进行离散;Yazdi等[7]将二阶显式有限体积法Godunov格式应用于水锤问题;潘存鸿[8]基于三角形网格的有限体积法建立具有空间二阶精度的Godunov格式;张大伟等[9]建立了基于 Godunov格式的一维、二维溃坝水流耦合数学模型;姜晓明等[10]基于Riemann近似解格式的一维、二维水流数学模型通过堰流公式进行耦合;Hwang[11]采用二阶精度格式对水锤问题进行分析;蒋明等[12]提出了一种求解管道耦合水力瞬变模型的 Godunov 计算格式;毕胜等[13]建立了Godunov格式下求解二维水流输运方程的高精度耦合数学模型;向小华等[14]基于显式的有限体积法以及TVD限制器构建了一维河网水流模型;Zhou等[15]通过等分控制体,并假定空穴仅出现在控制中心,实现了Godunov格式对管道内液柱分离现象的模拟分析。
本文采用Godunov格式和Riemann求解器对水锤方程进行数值求解,并提出了虚拟边界的处理方法。基于对算例的模拟分析,验证一阶、二阶Godunov格式在水锤模拟方面的准确性,研究库朗特数等参数的敏感性,并与MOC方法的模拟结果进行对比。
1 数 学 模 型
1.1 基本控制方程
描述管道水流状态的运动方程和连续性方程[16]可以写成矩阵的形式:
(1)
其中
式中:x为沿管轴线的距离;t为时间;H为测压管水头;V为管道内水流流速;a为波速;g为重力加速度;f为恒定摩阻系数;D为管道直径。
式(1)采用Riemann问题的求解方法[17],可以近似的写成如下形式:
(2)

有限体积法是将计算区域划分为多个控制体来对方程进行离散,然后对每个控制体进行积分。对于第i个控制体(图1),将式(2)沿x方向从控制边界i-1/2到控制边界i+1/2进行积分:
(3)
式中:fi-1/2为i-1/2界面数值通量;fi+1/2为i+1/2界面数值通量。

图1 计算区域的离散网格
(4)
式中:Δt为时间步长;Δx为每个控制体的长度;下标n、n+1分别表示t和t+Δt时刻。
1.2 一阶和二阶Godunov格式的通量计算
1.2.1 一阶Godunov格式
每个单元控制体具有统一的物理变量值,但是在两个单元控制体交界处的数值是间断的。为了计算出Godunov格式中的离散通量,可采用Riemann问题的求解方法[17],具体如下:
(5)
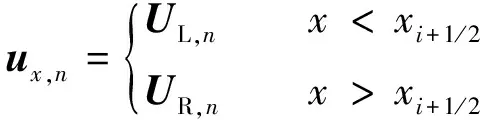
(6)
式中:UL,n为n时刻u在i+1/2界面左侧的平均值,UR,n为n时刻u在i+1/2界面右侧的平均值。t∈[tn,tn+1]时刻所有控制体界面i+1/2处的通量为

(7)
其中UL,n=Ui,nUR,n=Ui+1,n
由于采用单元内变量平均分布值替代界面左右的值,因此此格式只有一阶精度。
1.2.2 二阶Godunov格式
采用MUSCL-Hancock方法[17]进行线性插值重构,从而获得空间为二阶精度的Godunov格式,用MUSCL-Hancock方法进行线性重构的步骤如下:
第1步数据重构。为避免二阶格式在线性插值重构时出现虚假振荡的现象,引入斜率限制器函数MINMOD(σj,n,σj-1,n):
Ui,L=Ui,n-0.5ΔxMINMOD(σj,n,σj-1,n)
(8)
Ui,R=Ui,n+0.5ΔxMINMOD(σj,n,σj-1,n)
(9)
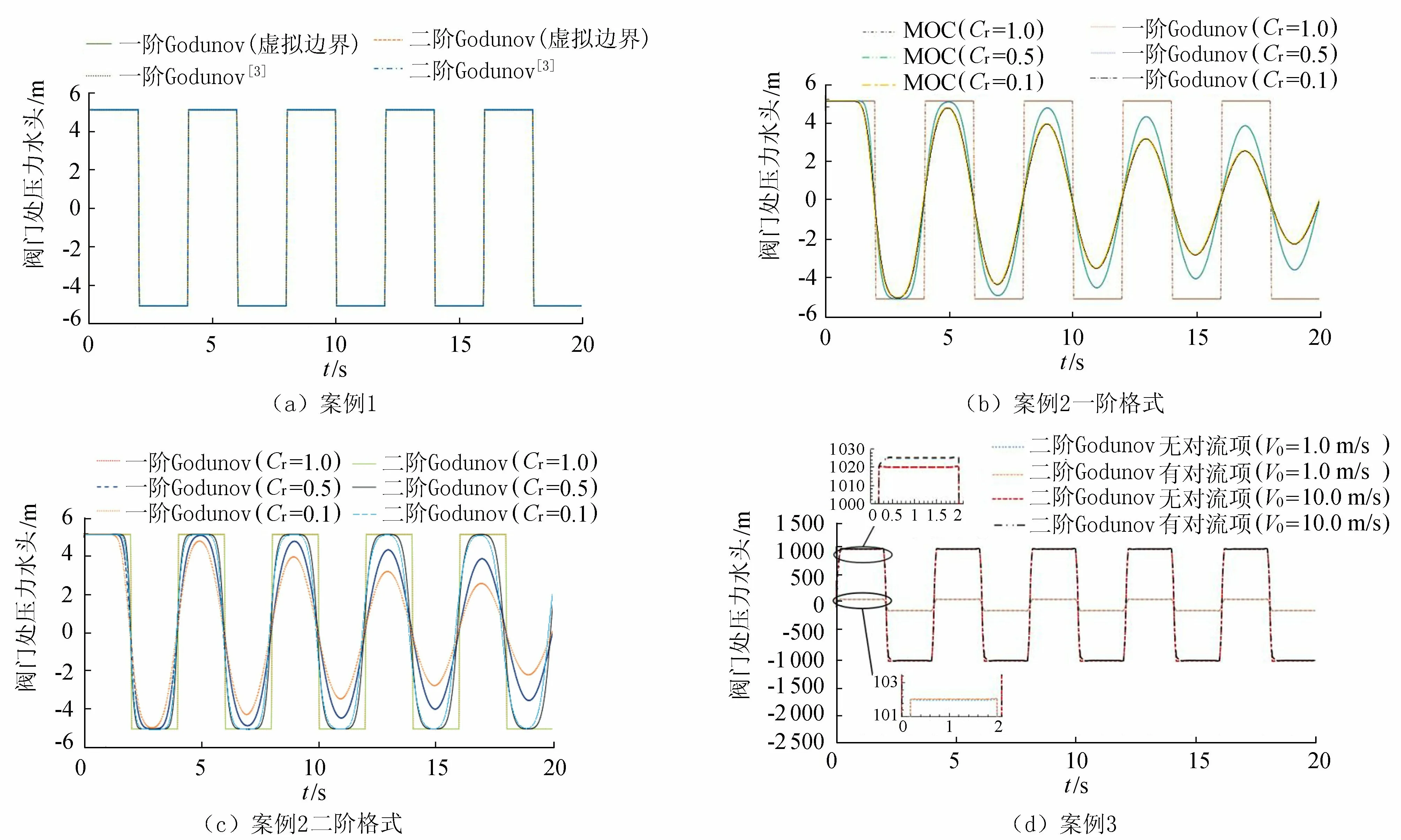
式中:下标L表示x→xi-1/2且x>xi-1/2;下标R表示x→xi+1/2且x 第2步推进时间计算: (10) (11) 第3步Riemann问题的近似求解: (12) 将式(12)代入式(7)中即可得到二阶Godunov格式在t∈[tn,tn+1]时刻所有控制体界面i+1/2处的通量。 在计算左右通量之后需要求n时刻到n+1时刻的解,对式(4)进行积分得: (13) 在有摩阻情况下采用显式的二阶龙格库塔法: (14) (15) (16) 如果采用一阶格式计算通量,则式(14)~(16)得到的格式在时间上为二阶精度,在空间上为一阶精度。如果采用二阶格式计算通量,则式(14)~(16)得到的格式在时间和空间上均为二阶精度。 时间步长应该满足CFL收敛条件,即: (17) 式中:Cr为库朗特数。 1.4.1 一阶Godunov格式边界处理 文献[3]需要通过Riemann不变量方程单独计算边界处的通量,然后计算其他单元控制体的通量。本文提出虚拟边界处理方法,可以使边界和所有单元控制体的通量值统一计算,采取的模型包含上游边界(上游水库)以及下游边界(末端阀门)。由式(7)可知,若想求得f1/2和fN+1/2,需要已知U0,n和UN+1,n,但是划分控制体时只包含单元控制体1至单元控制体N,因此如图2所示,在上游水库入口左边和管道末端阀门右边分别加入虚拟单元0和虚拟单元N+1。 图2 计算区域与虚拟网格 上游边界: U0,n=U1/2 (18) 根据负向特征线以及Riemann不变量方程可得: (19) 下游边界: UN+1,n=UN+1/2 (20) 根据正向特征线以及Riemann不变量方程可得: (21) 1.4.2 二阶Godunov格式边界处理 与一阶Godunov格式类似,二阶Godunov格式需要已知相邻的两个单元控制体内的数值,因此在上游水库入口左边和下游阀门右边分别加入两个虚拟单元0、-1和虚拟单元N+1、N+2(图2)。 上游边界: U-1,n=U0,n=U1/2 (22) 下游边界: UN+2,n=UN+1,n=UN+1/2 (23) 其中U1/2和UN+1/2的处理方法和一阶Godunov格式相同。 采用上游水库-管道-阀门的简化模型,管道长为1 000 m,计算区域单元数量为20,波速为a=1 000 m/s,上游水库水位Hr=0 m,初始速度为0.05 m/s,重力加速度g=9.806 m/s2,计算时间为20.0 s,下游阀门瞬间关闭。在数值模拟过程中假定:①即使低于水体汽化压力,也不发生液柱分离现象;②管道为无摩阻管道,则压力计算结果衰减均为数值计算耗散(误差)引起。 图3 三种案例阀门处水头变化 案例1:在初始速度V0为0.05 m/s的情况下,分别采用本文提出的虚拟边界处理方法和文献[3]的方法进行数值模拟,结果如图3所示。由图3(a)可知,虽然边界处理的方法不同,但压力计算曲线基本重合,说明本文提出的边界处理方法和文献[3]的计算精度相同,从而验证了虚拟边界的处理方法是准确可行的。而且文献[3]需要通过Riemann不变量方程得到边界处的通量值,然后将边界与其他单元分别进行计算,而本文通过虚拟边界的方法可以将边界和其他单元统一计算,对于计算和编程来说都更加简单方便。 案例2:基于MOC方法、Godunov的一阶和二阶格式计算Cr=1.0时阀门处的压力水头。由图3(b)可知,当Cr=1.0时,Godunov的一阶格式与MOC方法压力计算结果曲线完全重合。由图3(c)可知,当Cr=1.0时,Godunov的一阶格式与二阶格式压力计算结果曲线完全重合。说明Cr=1.0时,Godunov的一阶和二阶格式与MOC方法压力计算结果一致,再次验证了Godunov格式的准确性。 案例2:基于MOC方法、Godunov的一阶和二阶格式计算Cr分别为0.5和0.1时阀门处的压力水头。由图3(b)可知,在Cr分别为0.5和0.1时基于MOC方法与一阶Godunov格式的模拟结果完全相同并发生数值耗散,而且耗散量在Cr为0.1时比Cr为0.5时更多,说明Cr<1.0时数值出现耗散情况,二者耗散量相同,并且Cr值越小耗散量越多。 由图3(c)可知,在Cr=0.5和0.1时,一阶Godunov和二阶Godunov格式的模拟结果均出现数值耗散,且Cr值越小耗散量越明显。值得注意的是,二阶Godunov格式数值耗散远小于一阶Godunov格式的数值耗散,说明当Cr<1.0时,二阶Godunov格式模拟结果更加稳定,具有较强的鲁棒性。 综上所述,Cr<1.0时,3种方法均出现数值耗散,Cr值越小数值耗散越严重;一阶Godunov格式和MOC具有相同的计算精度,且均会产生较为严重的数值耗散,引起较大的计算误差;二阶Godunov格式能有效抑制数值耗散,具有较高的计算精度。 在一阶和二阶Godunov格式数值耗散相同的情况下,Cr=0.5,一阶格式的单元数量为2 000,CPU计算时间为27.86 s;二阶格式的单元数量为200,CPU计算时间为1.57 s。Cr=0.1时,一阶格式单元数量为500,CPU计算时间为16.98 s;二阶格式单元数量为50,CPU计算时间为1.36 s。上述结果说明,在计算精度相同的情况下,二阶Godunov格式CPU计算时间远小于一阶格式计算时间,具有较高的计算效率。这是因为,当库朗特数相同时,为了保证相同的计算精度(耗散量),二阶格式在计算中需要划分的单元数量比一阶格式的单元数量少很多,二阶格式需要很少的计算内存,因此,其计算速度快。 a. 根据Godunov格式的阶数在边界处增加相应数量的虚拟单元,使所有单元统一计算,无须在计算前单独对边界的数值进行处理,给水锤计算以及编程提供了方便,并且得到的模拟结果与文献[3]采用的边界处理方法得到的结果基本一致。这说明,本文提出的虚拟边界处理方法既保证了计算精度又避免了繁琐处理和计算,所以该方法可以广泛应用于基于有限体积法Godunov格式的边界问题的处理。 b. 分析库朗特数对模拟结果的影响,库朗特数Cr=1时,基于Godunov的一阶和二阶格式的模拟结果与MOC方法的模拟结果一致。库朗特数Cr<1时,一阶格式和MOC方法的数值耗散比二阶格式更严重。由于二阶格式进行了线性重构并且引入MINMOD函数,能够有效抑制衰减,所以得到的模拟结果最为稳定。此外,在相同的计算精度(数值耗散)情况下,二阶格式比一阶格式计算效率更高。 c. 分别计算分析有无对流项对关阀水锤模拟结果的影响,在马赫数(流速)较小时,对流项对结果几乎无影响,可忽略不计;随着马赫数增大,对流项的影响变大。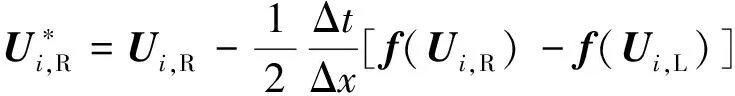
1.3 时间积分

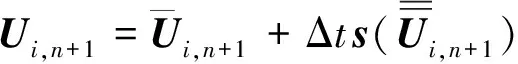
1.4 虚拟边界
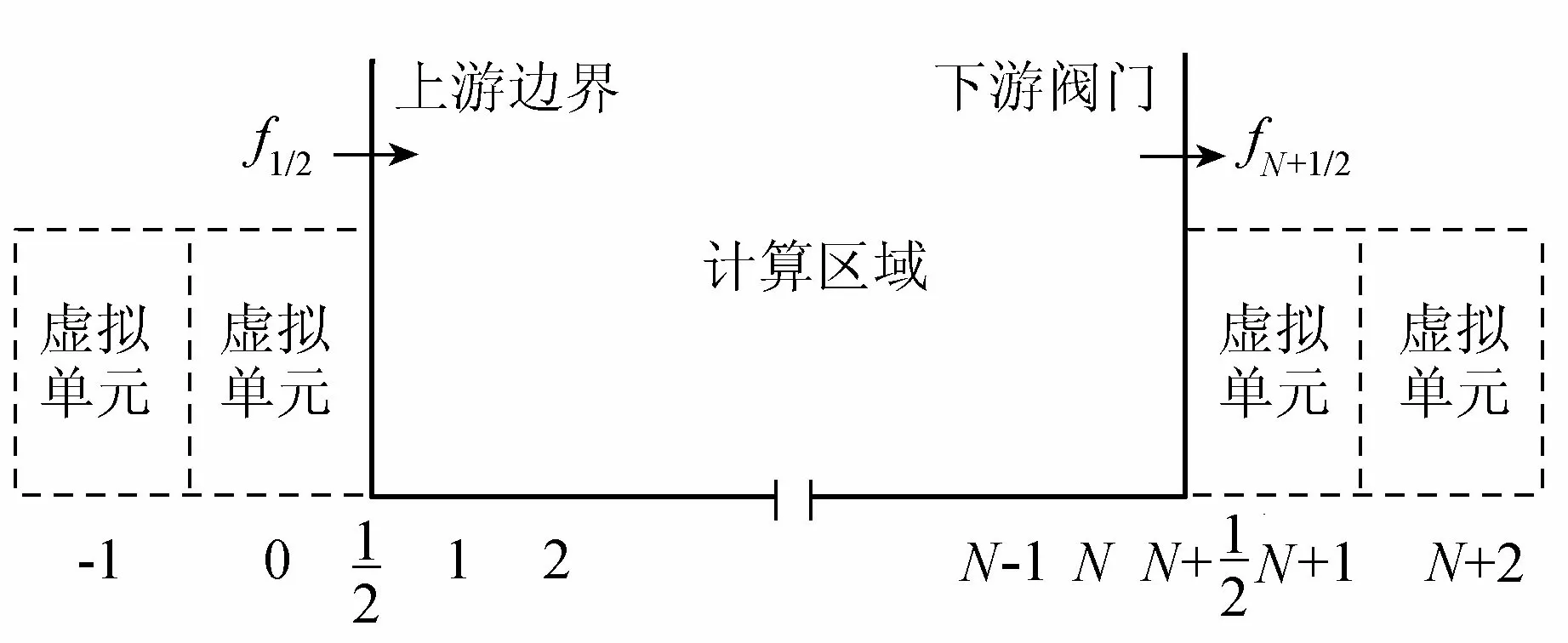
2 算例分析
2.1 模型准确性分析
2.2 参数敏感性分析
3 结 论
