大跨地铁隧道组合工法穿越断层时的围岩变形控制分析

2019-03-11唐晓杰陈佳玮李元海

隧道建设(中英文) 2019年2期

唐晓杰，石磊，陈佳玮, *，彭振，李元海

(1. 中国矿业大学力学与土木工程学院，江苏徐州 221116； 2. 中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州 221116； 3. 中交(广州)建设有限公司，广东广州 511458)

0 引言

断层破碎带是隧道施工过程中常见的不良地质现象，断层与断层周围岩体在物理力学性能上有较大差异，具有围岩地质条件差、地层由软岩到硬岩或由硬岩到软岩的过渡等特点[1]，而且工程环境及地质条件复杂且具有不确定性，由断层所引起的工程事故频发，给施工带来了重大损失，甚至造成人员伤亡。因此，开展对隧道穿越断层破碎带的围岩稳定性及其控制研究具有现实意义。

当前，国内学者对隧道穿越断层的相关问题进行了大量研究。为解决大断面隧道围岩变形控制及稳定性影响方面的问题，综合采用了理论分析、现场监测、数值模拟以及模型试验等手段，探讨了断层的发育规律[2]及断层对隧道围岩稳定[3-6]和支护结构变形的影响，并针对各实际工程情况提出了稳定控制方案。李文华等[4]研究表明，断层距离隧道2倍洞宽以内对围岩稳定性影响较大，断层倾角为45°左右时隧道围岩最稳定；黄生文等[5]通过有限元分析认为，断层存在使得位移应力分布极不均匀，隧洞原始应力分布也不对称，出现不同程度的应力集中，设计时应采用非对称性的超前加固措施并加大两侧衬砌厚度，以使隧道二次衬砌应力分布均匀化，并建议二次衬砌紧跟初期支护施工；丁远振等[7]采集大量的现场监测数据，分析认为高地应力区软岩隧道穿越断层地带时，隧道左右两侧围岩压力、支护内力与围岩变形呈现出很大的不对称性，采用优化断面形式、加强初期支护刚度、非对称预留变形量和锚杆布置等措施，可以有效减小隧道结构受力，控制隧道变形；熊炜等[8]针对断层错动量、断层倾角、隧道埋深以及隧道与断层的交角4个主要因素分别进行组合计算分析，认为4个因素对衬砌受力变形影响的敏感性依次减弱，并对衬砌的相对沉降量、纵向应力及剪应力进行分析计算，将衬砌的主要破坏模式分为拉张-挤压型破坏、直接剪断型破坏以及拉张-挤压与剪切结合的破坏形式。为解决隧道穿越断层的施工难题，现有研究多以具体工程为主要研究对象，针对隧道穿越断层时的施工工法[9-10]、风险评估[11]、临时支撑的稳定控制[12]以及工法转换[13-14]等方面进行研究。如崔振东[12]通过对大跨隧道双侧壁导坑法的数值模拟，研究了临时中隔墙岩柱开挖的稳定性和加固措施，并形成临时中隔墙岩柱开挖施工关键技术。相关文献对隧道穿越断层带的变形模式、震害机制[1]、突水突泥机制[15]、注浆加固机制[16]、隧道围岩破坏模式[17-18]等隧道穿越断层的相关问题也进行了一些研究。如张庆松等[16]通过断层泥注浆加固试验研究，认为注浆可显著提高断层泥的单轴抗压强度，注浆压力是提升加固效果的主控因素；宋瑞刚等[17]采用突变理论建立了含有断层破碎带围岩失稳的尖点突变模型，通过计算分析认为深埋隧道断层破碎带围岩的失稳是一种突发破坏现象；徐前卫等[18]通过模型试验得出，位于拱顶之上的断层下盘岩体在隧道开挖后呈悬挑状态，且靠近断层部位易出现拉裂缝，并且隧道开挖后，由于断层的阻隔作用，岩体应力在跨越断层上、下盘时呈不连续、非线性分布的特征。

现有研究对隧道穿越断层的稳定性控制已经取得了不少成果，但研究对象多为山岭公路、铁路隧道，对本文涉及的复杂工程环境下大跨地铁隧道相关研究较少，且鲜有针对不同工法组合和不同注浆厚度下大跨隧道穿越断层时围岩变形与控制的细致描述与分析，隧道围岩变形是工程中最直观的监控指标，上述问题仍有待深入研究。对隧道穿越断层段时围岩变形控制描述分析，有利于隧道围岩的稳定控制。

本文以深圳城市轨道交通2号线新秀站—莲塘口岸站区间(简称新莲区间)隧道为工程背景，此工程隧道断面跨度较大(19.5 m)，围岩软弱(Ⅳ、Ⅴ级围岩交错)，又位于房屋建筑集中地段，施工环境复杂，导致施工方法变换极其复杂，是国内罕见的复杂大跨地铁隧道工程。针对施工过程中遇到大跨地铁隧道穿越断层破碎带的围岩稳定性问题，需对隧道变形进行严格控制，采用FLAC3D软件进行三维模拟计算，针对实际工程采用的双侧壁导坑法转CD法再转双侧壁导坑法的工法组合，与工法组合1的全段双侧壁导坑法以及工法组合2的双侧壁导坑法转CD法进行对比分析，并针对1、3、5 m 3种注浆厚度的围岩变形进行对比，旨在分析评价新莲区间隧道工程穿越断层段的围岩变形控制及其工法组合和注浆厚度选择的合理性，并探求其围岩变形规律。

1 工程简介

深圳城市轨道交通2号线3期工程新莲区间长491.05 m，工程平面图见图1。隧道采用矿山法施工。隧道线路穿过猫窝山呈东西走向，工程区域为丘陵地带，地形起伏交错，地面高程为20～70 m，隧道埋深最大87 m、最小18 m，穿过的地层多为中、微风化石英砂岩，主要为Ⅳ、Ⅴ级围岩，岩石风化、破碎，节理、裂隙发育，局部为Ⅲ级围岩，地下水主要为基岩裂隙渗水。

在区间DK36+355～+361存在断裂，如图2所示。该断裂属于莲塘断裂组，走向北西，倾向北东，倾角为45°～55°，断裂性质为压扭性逆断层，为非活动性断层。该断裂对岩体的切割破坏作用较强烈，沿断层两侧岩体破碎，断层带风化可能加深，破坏了岩体完整性，降低了岩体强度。断裂部位地下水一般较为复杂，岩体完整性受地质构造影响较重，围岩稳定性大大降低，易产生坍塌或涌水。

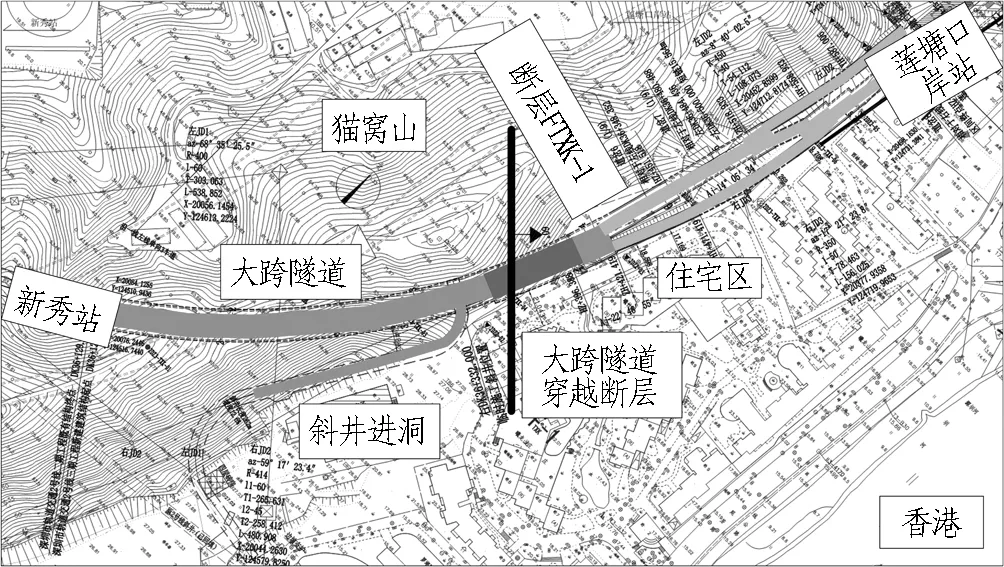
图1 新莲区间隧道工程总平面图

图2 隧道左线地质纵断面断层位置图(单位： m)

针对上述问题，制定施工对策如下： 1)断层带施工前，先探后挖，采用地质雷达和超前地质预报，做到预报长短结合，利用5 m长钻杆在掌子面超前钻探孔，结合地质钻机长孔钻探，根据地质预报和探测情况，采用合理的开挖方法和支护措施； 2)严格按照“严注浆、管超前、短进尺、弱爆破、强支护、紧封闭、早衬砌、勤预报和量测”进行施工； 3)支护完成后及时对支护背后注浆回填； 4)加强监控量测和掌子面地质素描工作，专人负责监测工作，及时分析、整理数据，及时反馈信息，以指导施工或采取措施； 5)建立健全应急预案，备好应急设备、物资，以备需要时抢险之用，同时隧道内设置应急救援管道和逃生管道，确保断层带施工人员安全； 6)经专家会议论证且经设计明确后方可实施断层带施工。

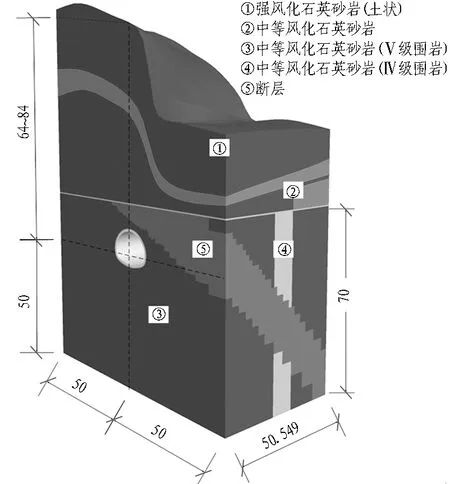
断层影响区域段主要为B5-B4-B5 3个断面段，该段为单洞3线大断面隧道，长度为51.549 m，跨度为19.532 m，高度为14.369 m，如图3所示。断层位于第1个B5断面段，B5断面段采用双侧壁导坑法开挖，至B4断面段转换为CD法，随后至B5断面段又转换为双侧壁导坑法。

图3 隧道断面示意图(单位： mm)

B4断面段隧道初期支护采用超前小导管+砂浆锚杆+型钢钢架+网喷混凝土。喷射混凝土等级为C25，厚0.32 m；小导管长3.5 m，环距为0.3 m，纵距为1.5 m，布置于隧道拱顶150°；系统锚杆长4.0 m，环距为0.8 m，纵距为0.75 m，梅花形布置于隧道的拱、墙；钢筋网采用双层φ10 mm@100 mm×100 mm网格；型钢钢架间距为0.75 m，对开挖轮廓外3 m范围内进行全断面注浆止水并加固土体。

B5断面段隧道初期支护采用双排超前小导管+型钢钢架+网喷混凝土，喷射混凝土等级为C25，厚0.32 m；小导管长4.0 m，环距为0.3 m，纵距为2.0 m，布置于隧道拱顶200°范围；边墙锚杆长4.0 m，环距为0.8 m，纵距为0.5 m，梅花形布置；钢筋网采用双层φ10 mm@100 mm×100 mm网格；型钢钢架间距为0.5 m，对开挖轮廓外3 m范围内进行全断面注浆止水并加固土体。

2 基于FLAC3D的数值模拟方法

2.1 问题分析

以隧道围岩位移为关键指标分析以下问题： 1)隧道过断层段不同工法组合的变形特点； 2)断层对隧道围岩稳定性影响规律； 3)断层段隧道注浆加固效果及加固圈厚度优化。

根据地质勘查以及设计资料，断层与隧道斜交，厚度约为5 m，位于Ⅴ级围岩区段，采用双侧壁导坑法开挖，在通过断层后5 m，围岩级别为Ⅳ级，长度为18.2 m，工法转换为CD法，CD法开挖8.2 m后，围岩级别变为Ⅴ级，再次进行工法转换为双侧壁导坑法，如图4所示。实际工程中，断层前后的岩体相对破碎，Ⅳ级围岩段掌子面岩体较为破碎，计算中扩大断层厚度为8 m。

实际工程中，对断层附近地下水进行引流措施，大大减小了其涌水水压，并且隧道围岩全断面注浆加固封堵裂隙以后，渗流水量较小。因此，计算中未考虑水的影响。

图4 断层位置及区段工法示意图(单位： m)

2.2 模拟方法

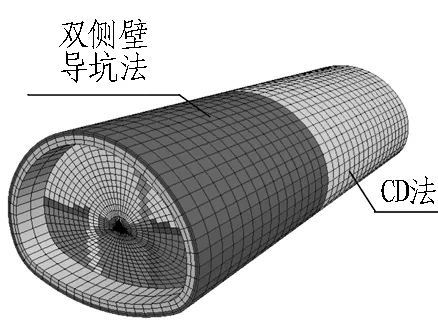
采用有限差分数值计算软件FLAC3D模拟围岩、锚杆、超前小导管、衬砌、断层等，并对双侧壁导坑工法和CD工法的开挖过程进行模拟。

围岩模型材料采用摩尔-库仑准则计算。隧道围岩主要为中风化石英砂岩，断层区域采取弱化围岩参数的办法模拟，注浆区域按照提升围岩等级的微风化石英砂岩参数近似，计算参数根据地质勘察报告中的岩土设计参数建议值表、施工过程揭露围岩描述、隧道位移实际监测结果以及相关研究的综合考虑确定，见表1。

对于钢筋混凝土复合支护以及型钢混凝土加强支护均使用实体弹性模型模拟，参数见表2。超前小导管采用Beam结构单元进行模拟，参数见表3。锚杆采用Cable结构单元进行模拟，参数见表4。

表1 计算模型中围岩物理力学性质指标

表2 衬砌结构参数取值

表3 超前小导管参数取值

表4 锚杆参数取值

地层材料的应力应变均在弹塑性范围内变化，地应力由输入初始边界应力后由FLAC3D进行初始应力平衡计算获得。模型地层按实际地层建模，其竖向应力按其自重应力取值。隧道开挖模拟通过FLAC3D中的Null实现。

2.3 几何建模

三维计算模型宽100 m，底部到计算地层分界面高70 m，分界面以上按照实际地层模型高度取值，隧道中线处埋深64～84 m。模型尺寸与支护结构如图5所示。模型实体单元总数为104 306个。模型边界条件如下：除顶面外其余5个面均约束法向位移。

(a) 实际工法支护结构

(b) 整体计算模型

Fig. 5 Sketches of tunnel crossing fault and supporting model (unit: m)

为探究大跨隧道采用不同工法组合穿越断层的变形规律，建立计算模型，如图6所示。分3种工况：图6(a)为实际工法，即双侧壁导坑法转换为CD法再转换为双侧壁导坑法；图6(b)为工法组合1，即全段双侧壁导坑法，不进行工法转换；图6(c)为工法组合2，即工法转换为CD法后不再进行转换，保持CD法开挖直到第2个B5段结束。各工法段开挖支护完成后再转换为其他工法开挖。

(a) 实际工法组合

(b) 工法组合1

为探究注浆厚度对大跨隧道穿越断层段的影响，模型计算时在掌子面前方和隧道周围进行预注浆，通过调整围岩参数的办法实现，分4种工况：未注浆和注浆1、3(实际工况)、5 m。实际工程中，先超前小导管注浆，然后在初次衬砌施工前，采用全断面加固压力注浆法，利用液压把能凝固的浆液均匀地注入岩土层中，以填充、渗透和挤密隧道围岩。注浆范围如图7所示。

超前小导管采用φ42 mm、厚度为3.5 mm的无缝钢管，管壁开花孔，梅花形布置，管长3.5 m，环距为0.3 m，纵距为2 m。钻孔仰角为10°～15°；浆液采用纯水泥浆，水灰比为0.5∶1；注浆终压为0.5～1 MPa。

全断面加固压力注浆法，采用水泥-水玻璃双液浆，水泥水玻璃配比为1∶0.6～1∶1(体积比)；普通硅酸盐水泥强度等级为32.5 MPa；水玻璃模数为2.6～3.0，玻美度为30～40 °Bé；注浆压力为0.8～2.0 MPa，达到注浆终压并继续注浆10 min以上；浆液扩散半径≥1 m，要求相邻注浆孔的浆液能形成交圈。注浆填充率为20%～40%，填充率根据实际地层情况以及现场试验确定。

(a) 横断面

(b) 注浆纵断面进尺

图7隧道围岩注浆范围示意图(单位： mm)

Fig. 7 Grouting range of tunnel surrounding rock (unit: mm)

2.4 开挖过程

开挖过程如图8所示。开挖进尺为3 m，隧道仰拱、隧底填充、底板紧随开挖进行，分别全幅一次施工，二次衬砌考虑台车连续施作，在隧道周边变形速率明显趋于缓和，水平收敛速度小于0.2 mm/d、拱顶下沉速度小于0.15 mm/d，累计位移值达极限相对位移值80%以上，并且初期支护表面的裂隙不再继续发展，方可施作二次衬砌。模拟过程中，将钢拱架、喷射混凝土等初期支护和临时支护用实体单元模型进行简化，双侧壁导坑法的左右导洞错开6 m模拟开挖，中间洞室的开挖滞后于右导洞的下部9 m(3个开挖步距)，二次衬砌的模拟滞后于中间洞室下部9 m。双侧壁导坑法左右导洞开挖至工法转换处，停止施工，等待中间洞室开挖至此，再进行CD法开挖，即各工法段开挖完成后再转换为其他工法开挖。

2.5 观测点布置

为对比分析隧道围岩变形，对模型布置观测点，如图9所示，提取测线网格节点作为观测点。在隧道纵向布置拱顶测线和拱腰测线，并选取3段围岩的中间位置断面，布置拱顶围岩位移测线和左右边墙围岩测线。

图8 隧道开挖步骤示意图

图9 隧道围岩测线位置布置图

3 数值模拟结果与对比

3.1 大跨隧道不同工法组合穿越断层的变形分析

3.1.1 变形场分析

为考察不同工法组合开挖后隧道围岩的变形特征，绘出围岩变形场，如图10所示。可以看出： 1)隧道拱顶的最大变形出现在Ⅳ、Ⅴ级围岩交界并与断层相交处，隧道拱底和拱腰的最大变形出现在Ⅴ级围岩与断层相交处，这些位置是变形控制的关键部位(见图10(a)白线框)，在施工中应重点关注。2)实际工法组合产生的最大变形为35 mm，工法组合1产生的最大变形为33 mm，工法组合2产生的最大变形为37 mm。双侧壁导坑法每一步开挖区域较小，对围岩扰动较小，对位移的控制优于CD法，所以工法组合1产生的变形最小，工法组合2产生的变形最大，实际工法组合居中。

为考察不同工法组合开挖后隧道围岩变形区域的形状与范围，绘出拱顶最大位移所在位置断面(Y=22.3 m)处的围岩最大剪应变云图，如图11所示。可以看出： 1)3种工法组合产生的变形区域形状均沿着断层区域分布，呈现出与断层走向一致的“枣核状”分布规律； 2)实际工法组合产生的变形影响范围最大为12.4 m，最小为5.0 m； 3)工法组合1的影响范围最大为11.5 m，最小为4.2 m； 4)工法组合2的影响范围最大为12.8 m，最小为4.4 m。工法组合1最小，工法组合2最大，实际工法组合居中。对比无断层的情况，其变形影响范围主要在隧洞周围相对均匀分布，拱顶围岩受地层偏压影响，但应变值远小于有断层的情况，拱腰处围岩的影响范围明显较小，变形的主要影响区域在断层范围内。

(a) 实际工法组合 (b) 工法组合1 (c) 工法组合2

(a) 实际工法组合 (b) 工法组合1 (c) 工法组合2 (d) 无断层段

图11不同工法隧道围岩最大剪应变云图

Fig. 11 Nephograms of maximum shear strain of surrounding rock with different tunneling methods

3.1.2 围岩轴向测点位移分析

为考察不同工法组合开挖后隧道拱顶的位移特点，绘出隧道拱顶竖向位移，如图12(a)所示。为考察不同工法组合开挖后隧道拱腰的位移特点，绘出隧道拱腰水平位移，如图12(b)所示。

(a) 拱顶竖向位移

(b) 拱腰水平位移

Fig. 12 Vertical displacement of tunnel by different tunneling methods

由图12(a)可以看出： 1)在0～20 m，3种工法组合均采用双侧壁导坑法，由于断层的存在，位移逐渐增大，但3种工法组合的位移基本相同； 2)最大竖向位移出现在22.3 m处，该位置是实际工法组合和工法组合2进行工法转换为CD法的位置，位移明显增大，并且工法组合2的位移值最大，实际工法组合居中，工法组合1最小； 3)通过断层后，3种工法的位移值明显下降，工法组合2的下降幅度小于工法组合1和实际工法组合； 4)随后在31.06 m处，实际工法又转换为双侧壁导坑法，位移逐渐趋近于工法组合1，而工法组合2因继续用CD法开挖，其竖向位移值明显大于实际工法组合和工法组合1； 5)离开断层约33 m后，3种工法的竖向位移值基本相同。

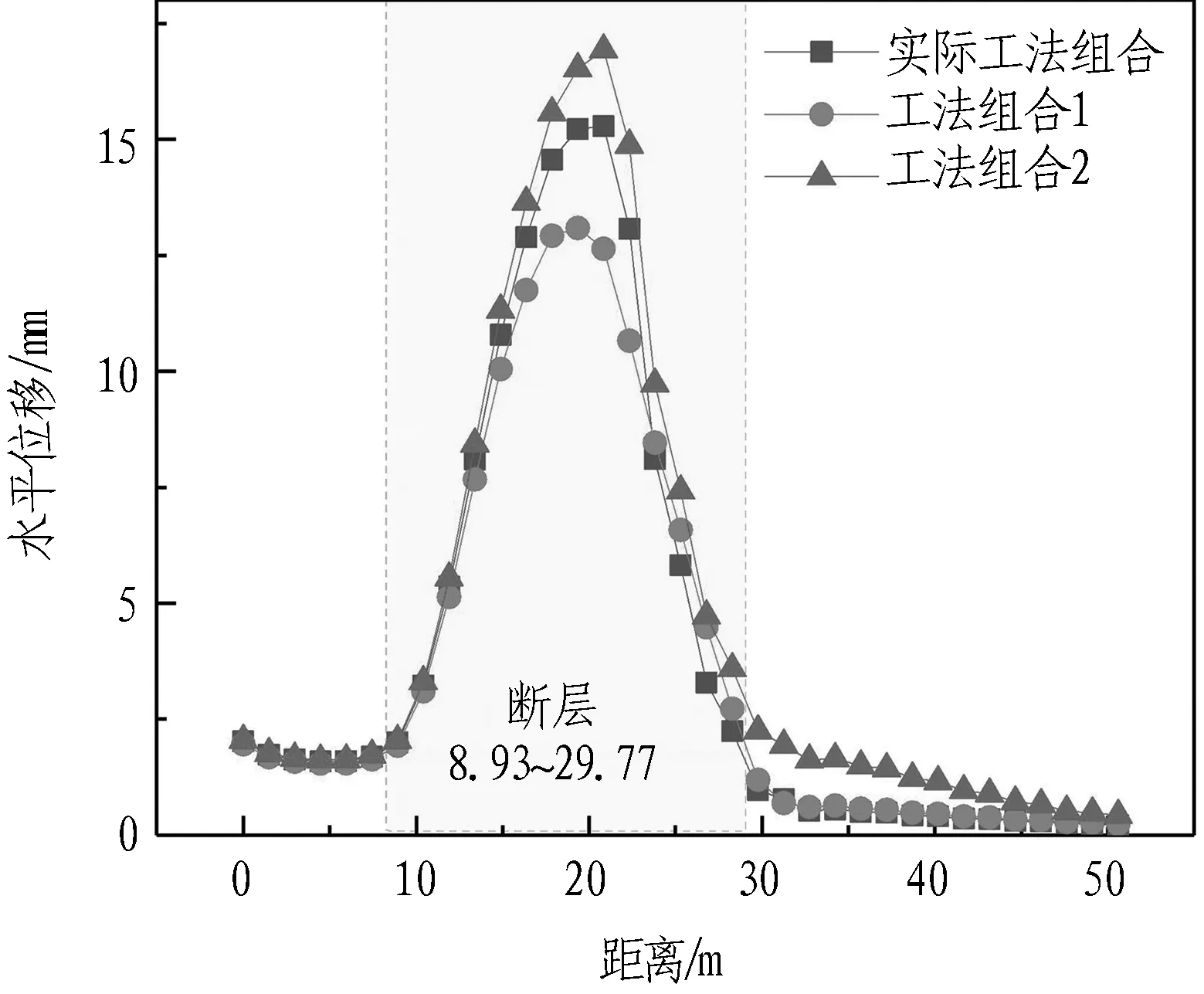
由图12(b)可以看出： 1)进入断层前，3种工法组合的水平位移基本相同； 2)进入断层后，位移逐渐增大，最大水平位移出现在21 m左右，工法组合2的位移值最大，实际工法组合居中，工法组合1最小； 3)在22.3 m处实际工法组合和工法组合2进行工法转换为CD法，实际工法组合与工法组合2的水平位移值下降趋势相近且幅度较大，说明CD法对水平位移的控制优于双侧壁导坑法； 4)在29.77 m处离开断层，3种工法组合的水平位移逐渐趋于平缓； 5)随后在31.06 m处，实际工法组合又转换为双侧壁导坑法，位移逐渐趋近于工法组合1，位移变化较为平缓，而工法组合2因继续用CD法开挖其水平位移明显下降，但整体控制不如双侧壁导坑法，其位移明显大于实际工法组合和工法组合1； 6)离开断层约19 m后，3种工法组合的水平位移值基本相同。

总的来说： 1)在第1段B5断面开挖完成后，工法转换为较“简易”的CD法是有意义的，但工法组合2后半段全用CD法开挖，位移明显较大，不利于隧道稳定，而且下一个变断面仍要进行工法转换； 2)工法组合1全程采用双侧壁导坑法，对位移控制较优，对比实际工法组合，虽然仅有8.2 m的工法转换为CD法，不利于工程进度，且位移大于工法组合1，但是总体上位移与工法组合1相差不大，有较好的经济效益。因此，在施工条件允许且基于节约人力物力的角度，该工法转换合理可行。

3.1.3 围岩断面测点位移分析

隧道拱顶围岩竖向位移开挖后的对比图如图13所示。可以看出： 1)无论何种断面，工法组合2的竖向位移值均为最大，实际工法组合居中，工法组合1最小； 2)距离隧道拱顶表面越远，其围岩竖向位移越小； 3)在图13(a)断面1位置时，3种工法组合均采用双侧壁导坑法，所以其竖向位移值相差不大； 4)图13(b)断面2位置处在拱顶刚出断层的Ⅳ级围岩段中部，在该段中实际工法组合和工法组合2均采用CD法，由于断层的存在，相比其他断面，其竖向位移值总体较大； 5)图13(c)断面3位置拱顶已经离开断层约18 m，3种工法组合的竖向位移变化区域平缓。

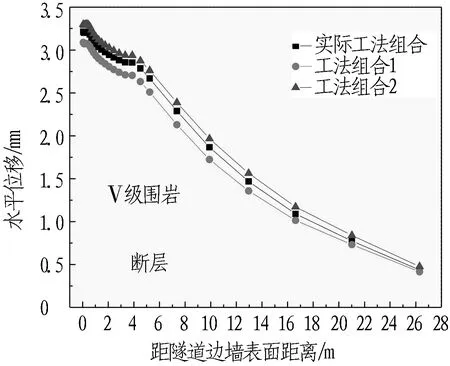
隧道左右边墙围岩水平位移开挖后的对比图如图14和图15所示。可以看出： 1)工法组合2的水平位移值最大，实际工法组合居中，工法组合1最小； 2)距离隧道边墙表面越远，其围岩水平位移越小； 3)对比图14(a)和图15(a)同一断面下有无断层2种情况，发现断层对水平位移有一定影响，在无断层的情况下，隧道围岩的最大水平位移出现在距离隧道边墙约2 m处； 4)对比图14(b)和图15(b)Ⅳ级围岩下断面2左右边墙围岩与断层的不同位置关系，发现距离隧道边墙约10 m后，有无断层对隧道围岩的水平位移影响不大，且工法组合1开挖所产生的围岩位移较大； 5)在图15(b)中，工法组合1的最大水平位移值大于其他2种工法，而断面2中实际工法组合和工法组合2采用CD法，说明CD法对水平位移的控制优于双侧壁导坑法，在该位置实际工法组合的水平位移最小，工法转换效果较好； 6)对比图14(c)和图15(c)Ⅴ级围岩下断面3左右边墙围岩与断层的不同位置关系，发现断层距离隧道边墙约13 m时，在有断层的情况下隧道围岩所产生的水平位移总体大于无断层的情况，但是在断层内水平位移的下降速率大于断层外，从图14(b)也可以得到这一规律。

(a) 断面1

(b) 断面2

图13隧道拱顶围岩位移测线对比

Fig. 13 Comparison of surrounding rock displacement of tunnel crown top

(a) 断面1

(b) 断面2

图14隧道右边墙围岩位移测线对比

Fig. 14 Comparison of surrounding rock displacement of tunnel right sidewall

(a) 断面1

(b) 断面2

图15隧道左边墙围岩位移测线对比

Fig. 15 Comparison of surrounding rock displacement of tunnel left sidewall

3.2 大跨隧道穿越断层注浆厚度影响

3.2.1 围岩变形场分析

为考察注浆对隧道变形的控制效果，绘出4种注浆厚度下隧道围岩变形场，如图16所示。可以看出: 1)未注浆时产生的最大变形为35 mm； 2)注浆1 m产生的最大变形约25 mm，相比未注浆时降低28.6%； 3)实际工法注浆3 m产生的最大变形约20 mm，相比未注浆时降低42.9%； 4)实际工法注浆5 m产生的最大变形约18 mm，相比未注浆时降低48.6%。

为考察注浆对隧道变形区域形状与影响范围的控制效果，绘出拱顶最大位移所在位置断面(Y=22.3 m)处的隧道围岩最大剪应变云图，如图17所示。可以看出： 1)4种注浆厚度产生的变形区域形状均沿着断层区域分布，并且随着注浆厚度的增加，变形区域逐渐减小，由与断层走向一致的“枣核状”(图17(a)、17(b))变为较均匀的“椭圆形”(图17(d))； 2)未注浆时的变形影响范围最大为12.4 m，最小为5.0 m； 3)注浆1 m的变形影响范围最大为7.7 m，最小为4.9 m； 4)注浆3 m的变形影响范围最大为6.3 m，最小为2.2 m； 5)注浆5 m的变形影响范围最大为3.3 m，最小1.9 m。

总的来说，注浆后的隧道围岩变形降低明显，注浆对断层附近围岩变形的控制效果明显，而且注浆厚度越大，围岩变形控制效果越好，说明注浆对强度低的软弱破碎围岩加固效果较为显著。

(a) 未注浆 (b) 注浆1 m (c) 注浆3 m (d) 注浆5 m

图17不同注浆厚度隧道围岩最大剪应变云图

Fig. 17 Nephograms of maximum shear strain with different grouting thicknesses

3.2.2 轴向测线围岩位移分析

为考察注浆对隧道拱顶的变形控制效果，绘出隧道开挖后的拱顶竖向位移，如图18(a)所示。可以看出： 1)在0～4.47 m进入断层前，各工况有无注浆的围岩竖向值相差不大； 2)在4.47～25.31 m进入断层后，隧道拱顶的竖向位移迅速增加，最大竖向位移出现在21～25 m，该位置为Ⅳ、Ⅴ级围岩交界处附近； 3)隧道未注浆时，其竖向位移增长最快，位移值最大，注浆后位移增速明显下降，但注浆1 m时，其最大位移值明显超过了20 mm的竖向位移控制值，注浆3 m和5 m对位移的控制效果相对较好； 4)在25.31 m通过断层后，各工况竖向位移值迅速下降，并在31 m附近趋于平缓。

为考察注浆对隧道拱腰的变形控制效果，绘出隧道开挖完成后的拱腰水平位移，如图18(b)所示。可以看出： 1)在0～8.93 m进入断层前，各工况有无注浆的围岩水平值相差不大； 2)在8.93～29.77 m进入断层后，隧道拱腰的水平位移迅速增加，最大水平位移出现在20～22 m，该位置是Ⅳ、Ⅴ级围岩交界处附近，在过了峰值后，各工况水平位移均呈现下降趋势； 3)隧道未注浆时，其水平位移增长最快，位移值最大，注浆后位移增速明显下降； 4)在29.77 m通过断层后，各工况水平位移趋于平缓，且位移值相差不大。

(a) 拱顶竖向位移

(b) 拱腰水平位移

Fig. 18 Longitudinal displacement of surrounding rock with different grouting thicknesses

总的来说： 1)与未注浆相比，在断层区域注浆加固效果最为明显，在进入断层前和离开断层后，注浆对围岩竖向位移控制有一定效果，而对围岩水平位移控制没有明显作用； 2)在断层区域，随着注浆厚度的增加，围岩位移逐渐减小，但1 m注浆厚度超过了竖向位移控制值，而5 m注浆方案与3 m注浆方案相比效果提升不大，围岩位移控制效果差异很小。

3.2.3 基于位移控制率的注浆效果分析

为定量描述3种注浆方案对隧道围岩位移的控制效果，定义围岩某点的位移控制率指标为n，按式(1)计算。n>0表示注浆能够控制位移的正向作用，采用注浆后位移下降的值与未注浆的位移值相比来表示注浆后位移的控制提升效果。

n=1-dx/d0。

(1)

式中：n为某点位移控制率；dx为隧道围岩注浆厚度为x时的位移值；d0为隧道围岩未注浆时的位移值。

隧道拱顶围岩位移控制率对比如图19(a)所示。隧道拱腰围岩位移控制率对比如图19(b)所示。

(a) 拱顶竖向位移

(b) 拱腰水平位移

Fig. 19 Comparison of vertical displacement control rate of surrounding rock

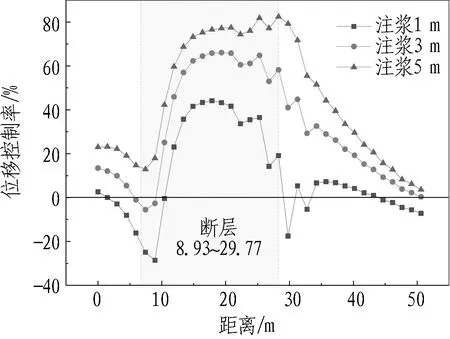
由图19(a)可以看出： 1)在断层区域，注浆后的位移控制率较高，注浆5 m的控制率达70.6%； 2)出断层后围岩控制率区域平缓，说明注浆对拱顶竖向位移的控制持续有效，注浆3 m的围岩控制率在30%左右，注浆1 m的围岩控制率仅20%左右。

由图19(b)可以看出： 1)注浆后断层区域内的位移控制率明显高于断层外，但是出断层后，3种工况的位移控制率迅速下降，并最终趋于0，说明注浆对软弱围岩的水平位移控制效果较好，但是对正常围岩的水平位移控制效果不明显； 2)注浆1 m的情况下存在多处控制率为负的情况，说明注浆1 m的水平位移控制效果与未注浆相比，提升不大，甚至还有增大水平位移变化的趋势。

隧道拱顶和拱腰不同区域的位移控制率均值如表5和表6所示。可以看出： 1)在断层区域内，注浆5 m的控制率均值与注浆3 m的控制率均值相差不大，但远高于注浆1 m； 2)断层区域内的控制率均值明显高于断层外的控制率均值。

表5拱顶围岩位移控制率均值表

Table 5 Mean value of displacement of surrounding rock around crown top

部位位移控制率/%注浆1 m注浆3 m注浆5 m断层区域30.2651.3860.52出断层后18.7829.7237.68

表6拱腰围岩位移控制率均值表

Table 6 Mean value of displacement of surrounding rock around arch waist

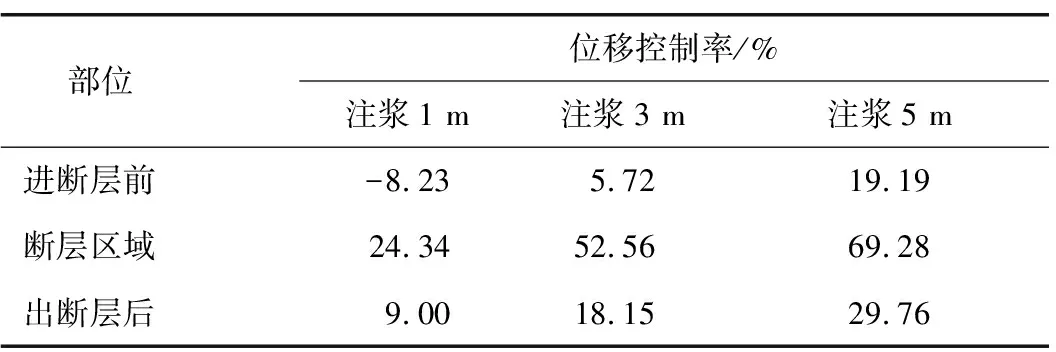
部位位移控制率/%注浆1 m注浆3 m注浆5 m进断层前-8.235.7219.19断层区域24.3452.5669.28出断层后9.0018.1529.76

位移控制率均值可定量描述一定区域内注浆的总体效果，可从围岩位移控制的角度直观地评价注浆效果，区域位移控制率的计算公式如式(2)所示。

(2)

式中：N为某区域内位移控制率均值；a为区域范围下限；b为区域范围上限；n(x)为位移控制率关于距离的函数解析式。

综上所述，1 m注浆厚度位移值超限且效果较差，3 m注浆厚度效果明显，5 m注浆厚度提升不大。为避免浪费，实际采用3 m注浆厚度是安全合理的。

3.3 现场监测数据对比分析

隧道围岩变形的监测数据包含了隧道施工力学演化过程和围岩变形特征的最全信息。新莲区间隧道在里程DK36+350～+405的围岩变形历时曲线如图20所示。监控测点断面间隔10 m布置，为便于描述，编号为1—6。断层在DK36+355～+361，监测断面1、2在断层区域附近；Ⅳ级围岩CD工法段在DK36+374.2～+382.4，监测断面3、4在此区域内；监测断面5、6为Ⅴ级围岩双侧壁导坑工法段。

(a) 拱顶沉降

(b) 净空收敛

Fig. 20 Time-history deformation curves of tunnel surrounding rock

由图20可以看出： 1)各监测断面拱顶沉降和拱腰收敛的变化趋势基本相似，在监测前期(0—50 d)，各断面拱顶沉降值相差不大，监测断面1、2的拱腰收敛值明显高于监测断面3、4，说明CD法开挖后对水平收敛的控制较好； 2)在监测中期(50—100 d)，各监测断面变形值迅速增大并逐渐趋于平稳，监测断面1、2的沉降值开始平稳增大； 3)监测后期(100—225 d)，随着Ⅴ级围岩段的开挖，各断面均出现变形最值，随后趋于平缓。

不同区域隧道断面的变形监测对比如表7所示。可以看出： 1)模拟值明显高于实测值，尤其是断层区域，原因在于，对模拟开挖过程进行了一定的简化，为突显断层的影响效果以及不同工法组合的控制效果，对断层区域的围岩参数弱化较大，而实际施工中对位移控制措施较为严格； 2)隧道变形规律基本一致，断层区域的变形值最大，Ⅳ级围岩CD工法段距离断层较近，所以位移值均大于远离断层的Ⅴ级围岩双侧壁导坑工法段； 3)新莲区间隧道的拱顶沉降和拱腰收敛均控制较好，监测断面1、2的变形值明显高于其他断面，拱顶沉降较为明显(见图20(a))，说明断层对隧道围岩变形有一定影响，对拱顶沉降影响较大，与数值模拟结论一致，在施工中应重点关注； 4)监测断面3、4与监测断面5、6的最终变形值相差不大，说明Ⅳ级围岩工法转换为CD法和Ⅴ级围岩段采用的双侧壁导坑法均有较好的适应性，实际工程所采用的工法合理可行。

表7隧道变形监测对比

Table 7 Comparison between monitoring data and numerical results of tunnel deformation mm