含主动悬架的汽车振动结构虚拟激励仿真*

秦玉英 陈双

（辽宁工业大学汽车与交通工程学院）

随着生活质量的不断提高，人们对汽车乘坐舒适性的要求逐渐提高。悬架结构是影响汽车乘坐舒适性的主要部分。相对于被动悬架，主动悬架可通过调整控制力来改变悬架的阻尼和刚度，从而改善汽车的使用性能。文献[1-2]给出了主动悬架控制策略对汽车乘坐舒适性的影响，以及时域的响应，但无法看出在频域内汽车振动响应的统计关系。虚拟激励法[3]的精髓在于构造一种虚拟激励，以结构的频率响应函数为桥梁，获取虚拟响应，由虚拟响应的共轭乘积来获取真实响应的功率谱密度。应用虚拟激励法理论进行随机振动分析在近些年较为多见，无论汽车振动结构具体如何，都是适用的，但针对含主动悬架的汽车随机振动分析很少。因此，文章应用虚拟激励法基本理论，对含有主动悬架的汽车随机振动进行了仿真分析。

1 虚拟激励法基本理论

设振动结构的平稳随机激励的x（t）自功率谱密度Sx（f）已知，对应给出虚拟激励：

式中：t——时间，s；

j——虚数单位；

f——频率，Hz。

在x（t）作用下，由式（1）建立振动结构实际响应y（t）的虚拟响应：

式中：H（f）——y（t）与x（t）之间的频率响应函数。

y（t）的功率谱密度为：

式中：*——函数的共轭。

由式（1）可知，只要给定实际激励的统计特性，便可构造虚拟激励。通过激励与响应之间的频率响应函数建立虚拟响应，由虚拟响应求取真实响应的统计特性，可见虚拟激励法的灵活性。

2 含主动悬架的汽车振动结构模型

2.1 汽车振动结构力学模型

图1示出含有主、被动悬架的1/4 汽车2 自由度结构。

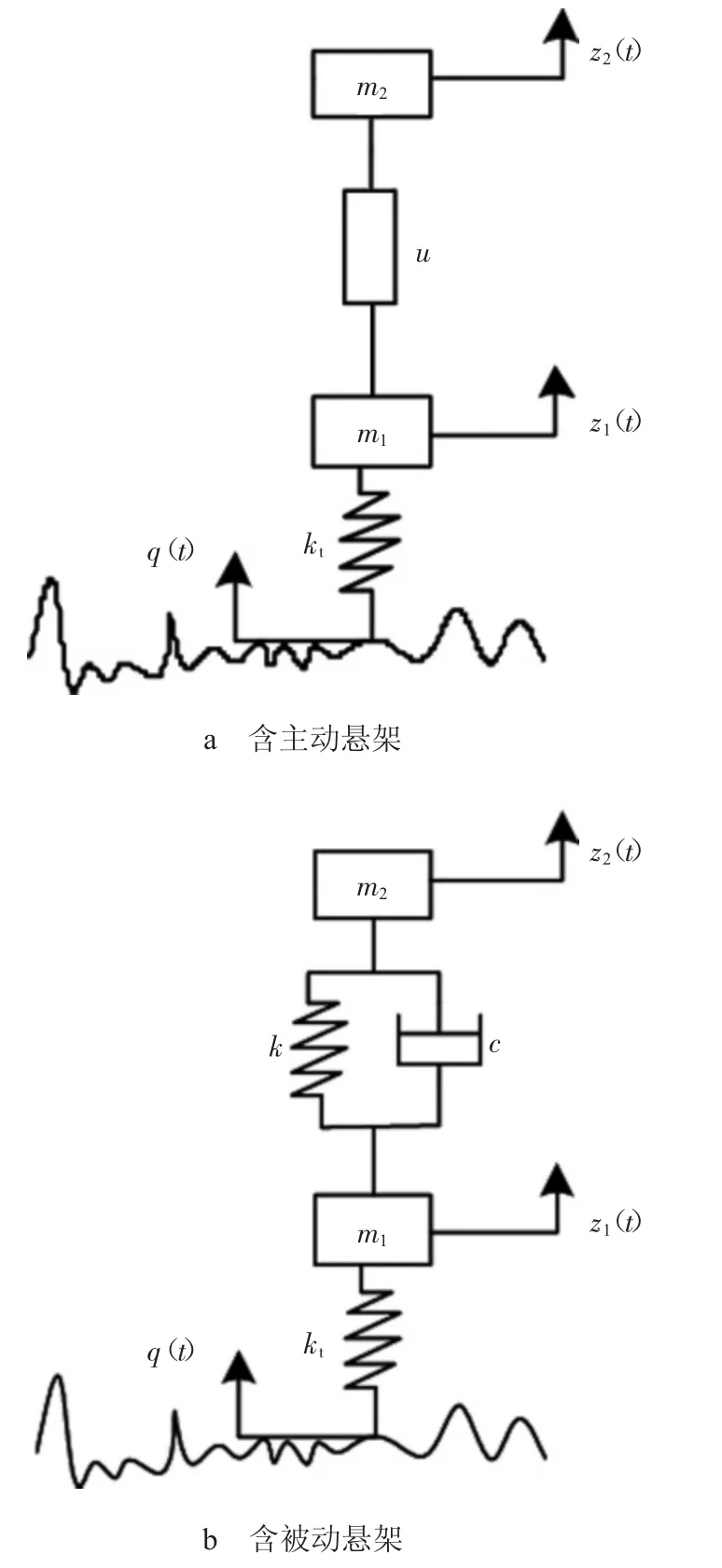
图1 1/4 汽车2 自由度力学模型

2.2 汽车振动结构微分方程

由牛顿定律建立含主动悬架的2 自由度数学模型：

式中：l1，l2，l3——反馈系数。

将式（4）和式（5）进行整理，则汽车振动结构微分方程为：

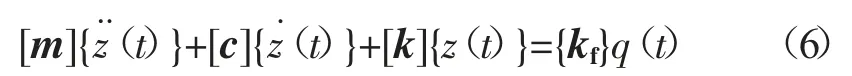
其中：{z（t）}={z1（t）,z2（t）}T

式中：[m]，[c]，[k]——质量矩阵、阻尼矩阵、刚度矩阵；

{kf}——右端与路面激励对应的矩阵；

q（t）——路面激励。

[m]，[c]，[k]，{kf}的具体表示分别为：

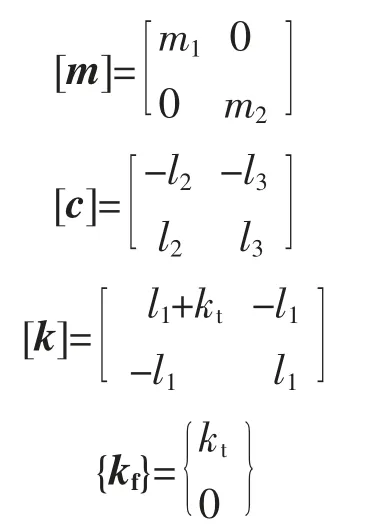
3 虚拟激励法的应用

3.1 虚拟路面激励的构造

汽车振动输入的路面不平度，主要采用路面功率谱密度（Gq（f））描述其统计特性[4]。

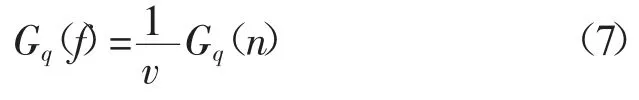
式中：Gq（n）——路面不平度的空间功率谱密度；

n——空间频率，Hz；

v——车速，km/h。

由式（1）构造路面对汽车的虚拟激励：

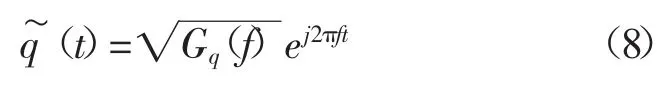
3.2 虚拟响应量

由式（2）可得1/4 汽车2 自由度结构虚拟响应为：

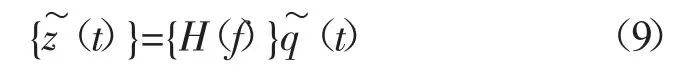
由式（9）可得虚拟车身垂直加速度响应为：

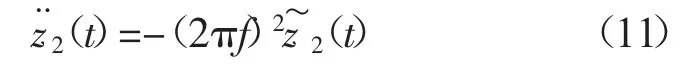
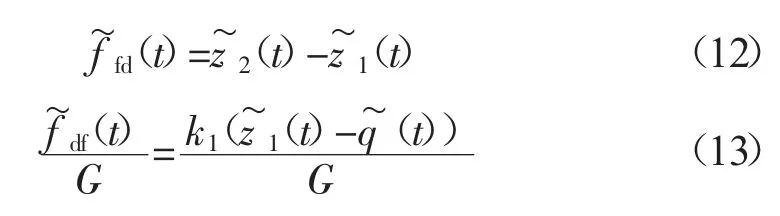
其中：G=（m1+m2）g

式中：G——车轮的静载，N。

3.3 响应量的统计特性

式（11）～式（13）得到的振动响应量的功率谱密度与傅里叶分析方法相同，但从推导过程可见虚拟激励法只是简单的代数关系运算，因此，如将虚拟激励法应用到多自由度系统求取响应量的统计特性不仅简单，且会降低很大的工作量。

振动响应量的均方根值为：

式中：f1，f2——频率的下限和上限，Hz。

4 汽车随机振动分析

为说明本方法的可行性，给出某车的仿真参数：m1=24 kg，m2=240 kg，k=9 475 N/m，kt=85 270 N/m，l1=7 592 N/m，l2=-481 N·s/m，l3=1 916 N·s/m，c=754 N·s/m。汽车以90 km/h 的速度行驶在B 级路面上，图2 示出含主、被动悬架的汽车振动响应量的功率谱密度曲线。表1 示出不同车速时振动响应量的均方根值。从图2和表1 中可知，接近车身和车轮固有频率（1.5 Hz）位置处产生峰值。在车身固有频率处，含有主动悬架的振动响应量的峰值均有明显下降，说明主动悬架对提高乘坐舒适性作用明显，但车轮相对地面的抓地性能没有改善，即可能损失了一部分汽车的行驶安全性能。

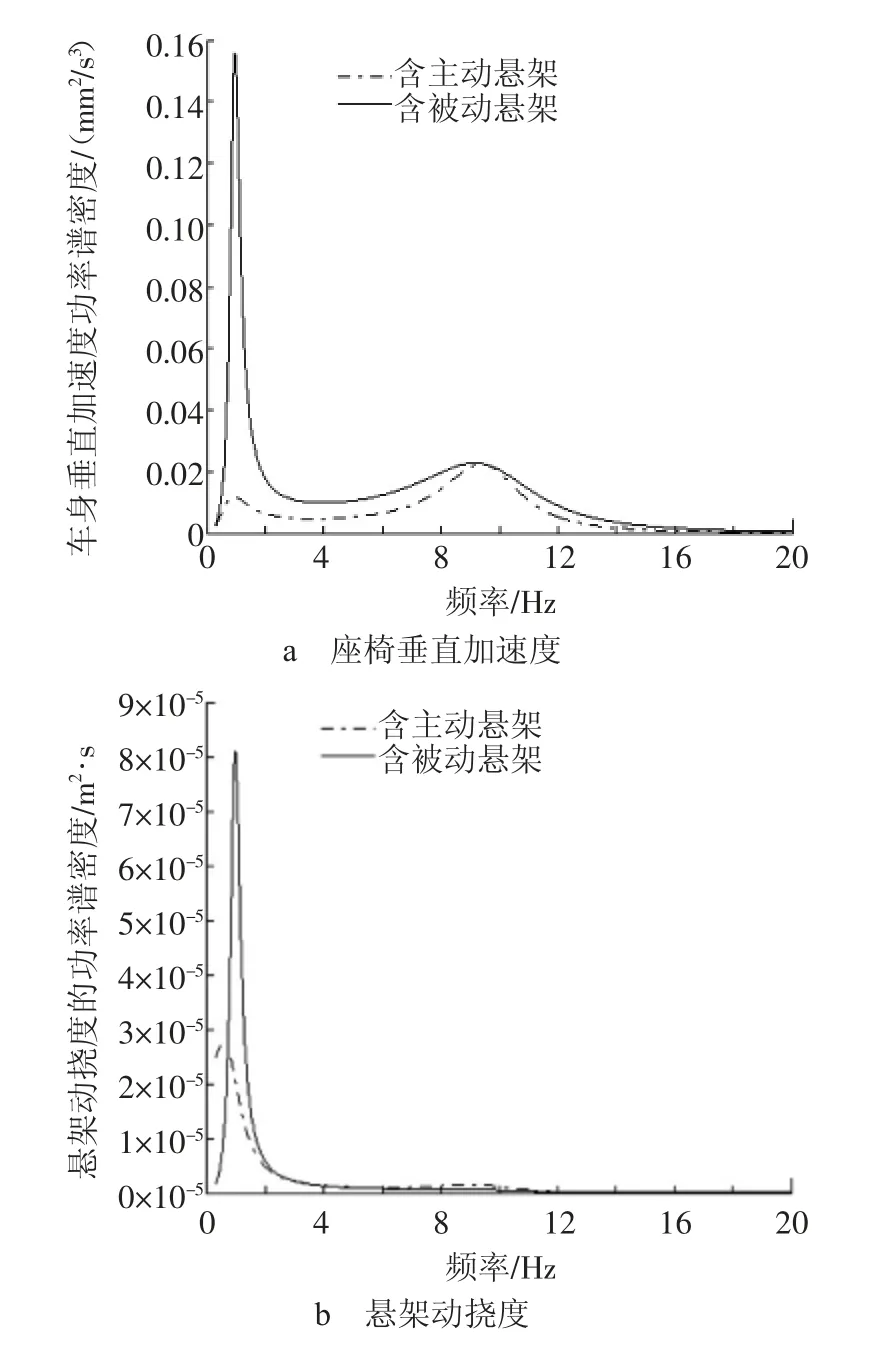
图2 含主、被动悬架的汽车振动响应量的功率谱密度曲线

表1 汽车振动响应量的均方根值

5 结论

文章应用虚拟激励法基本理论，构造了虚拟的路面激励，针对含主动悬架的汽车振动结构的微分方程，求取振动响应的统计特性，方法简单。为验证方法的可行性，以含主动悬架的汽车2 自由度模型为研究对象，简单而有效地应用虚拟激励法理论求出了汽车振动响应量的统计特性，并进行了行驶平顺性的仿真分析。由此，提供了一种针对含主动悬架的汽车振动结构进行随机振动分析的方法。