交叉口无干扰条件下右转机动车轨迹建模

罗瑞琪，刘 岩，孟维伟，朱晓东

（1.中国市政工程华北设计研究总院有限公司，天津市 300110；2.天津市市政工程设计研究院，天津市 300041）

0 引言

车辆行驶轨迹仿真是仿真模型的重要组成部分，是动态模拟车辆微观行为的前提和基础。其中，转弯车辆是信号交叉口产生冲突的主要原因，是信号交叉口仿真分析的重要内容，但左转车辆轨迹受多种因素影响，变化范围大，难以用数学模型准确表示[1]。右转车辆轨迹受几何条件影响，具有距离短、变化范围小等特点，因此建立右转轨迹模型，可以使得交通状况得以更好的再现，为交叉口的转角、转弯半径的设计和右转车辆的信号控制提供依据。

国内外研究学者对于右转车辆的研究主要集中在以下两个方面：一方面是分析右转车辆与行人和非机动车冲突行为，建立延误模型[2-4]；另一方面是通过分析右转车辆与行人和机动车的干扰行为，提出信号交叉口右转车辆的控制条件[5-7]，为信号控制提供依据。Stover等[8-9]对不同交叉口的右转轨迹数据进行了调查，大量数据表明该轨迹受多种因素的影响，且其变化会对其他道路使用者造成干扰，因此在交叉口设计中，应将车辆转弯轨迹作为重点考虑因素之一。Walton等[10]和Read[11]利用视频采集技术，对不同信号交叉口的不同车型车辆右转轨迹进行调查，结果显示转弯车辆轨迹与车辆类型、交叉口几何条件等因素有关。随着人们对微观行为研究的深入，Alhajyaseen等[12]对不同交叉口右转车辆轨迹进行调查，将右转车辆轨迹用欧拉曲线、圆曲线、直线段来表示，且假设曲线参数满足正态分布，分布参数与交叉口几何条件和交通条件等因素有关。

综上所述，国内外对于右转机动车的研究主要集中于冲突行为以及信号控制方面，对于轨迹方面的研究甚少，并且未建立具体的轨迹模型。因此本文将以大量数据为基础，利用视频检测技术，结合Track pro软件对不同几何条件交叉口无行人、无非机动车干扰下的右转车辆轨迹进行追踪，选取合适模型对右转车辆轨迹进行描述，分析右转轨迹的影响因素，并结合实测数据建立影响因素与模型参数的映射关系，建立无干扰下右转车辆轨迹模型。右转车辆轨迹模型可以很好地描述不同几何条件交叉口右转车辆的轨迹行为，为微观仿真提供理论支持。

1 数据采集

1.1 调查地点

调查地点位于苏州市。调查地点在交叉口几何布局方面存在很大不同，如转弯半径、交叉口转角、出口道数目等，这种布局上的变化对于分析右转车辆的轨迹模型极为重要。

参照图1调查交叉口的几何条件，建立坐标轴，O为坐标轴原点，θ为交叉口转角，即右转出口道中心线与进口道中心线（交点为r）所形成的夹角，rad；A为出口道中线与停止线交点，B为进口道中线与人行道内侧边缘线交点；C为O与B两点之间的水平距离，m；D为O与A两点之间的垂直距离，m。

图1 交叉口几何参数定义示意图

1.2 数据获取方法

Track pro是基于视频采集获得行人或车辆时空数据的分析软件，利用该软件可以获得车辆的位置坐标、速度、位移等数据。数据获取方法主要有以下4个步骤（见图2）：（a）选取合适调查地点和调查时间，拍摄视频；（b）结合视频检测技术，利用Track pro软件，建立坐标轴，以进口道停车线和右转车道内侧车道线交点为原点，右转车辆出口道方向为x轴，垂直方向为y轴；（c）根据视频观测角度，通过标定，将像素坐标转变为地理坐标；（d）采集转弯车辆位置坐标点及对应点的速度值，计算平均位置坐标，从而获得车辆平均轨迹。

车辆轨迹由一系列时空点组成，采样间隔0.12 s。因所有视频观测点均为交叉口高处建筑，观测角度大，考虑到转弯车辆尺寸，将车辆前部中心处为位置参考点。本文研究内容为无行人、无非机动车干扰时右转轨迹模型，因此在数据提取时，选取无行人、无非机动车干扰情况下的轨迹数据。为简化模型，仅对小型车右转数据进行调查。

图2 数据获取方法示意图

本文需对相同进口道、出口道的右转车辆平均位置坐标及平均速度进行计算，平均速度为所有右转车辆速度的平均值；结合图2建立的坐标轴，统计n条轨迹数据，假设n=3，在同一坐标系中计算不同轨迹点、相同横坐标下的平均纵坐标，最后得到一系列平均轨迹坐标点，平均轨迹坐标点的连线即为调查地点转弯车辆的平均轨迹。以星明街-现代大道西侧进口道右转车辆为例，利用软件，对110辆右转小汽车的右转数据进行统计，则得到110组数据（n=110），利用上述方法计算平均轨迹坐标点，共得到20个坐标点，计算结果如表1所示，坐标点的连线即为该地点右转车辆的平均轨迹。

2 右转机动车轨迹模型

2.1 轨迹影响因素分析

本文针对交叉口无干扰条件下右转车辆轨迹进行建模，因此不考虑行人和非机动车的影响，仅将交叉口尺寸以及车辆速度作为右转轨迹的影响因素。通过调查，交叉口转角、转弯半径、出口道数目、车辆速度是车辆轨迹的主要影响因素。其中因交叉口实际状况，转弯半径较难准确测量，因此定义参数C和参数D（对于同一进口道、不同出口道右转轨迹的影响因素也可以用参数C和D来表示），将交叉口转角θ、距离D、距离C、速度V这4个参数作为右转车辆轨迹影响参数。

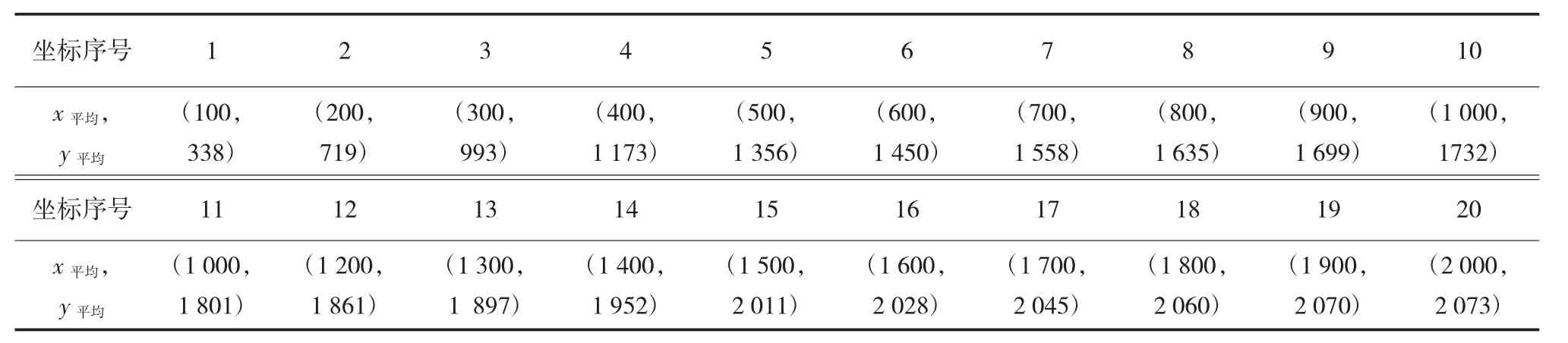
表1 右转车辆平均轨迹坐标点cm

2.2 轨迹模型建立

通过调查轨迹数据，分别用对数函数、二次多项式对调查地点轨迹进行拟合，拟合结果如表2所示。在置信度为95%情况下，利用对数函数拟合，相比二次多项式拟合效果要好，因此最终确立右转机动车轨迹模型为：

式中：x为横坐标，cm；y为纵坐标，cm；a，b 为模型参数。

根据实测数据，统计得到轨迹模型参数a值随转角θ、距离C、距离D和速度V的增加而增加，轨迹模型参数b值随转角θ、距离C、距离D、速度V的增加而减少。因此a值、b值与4个轨迹影响因素的关系可以表示为：

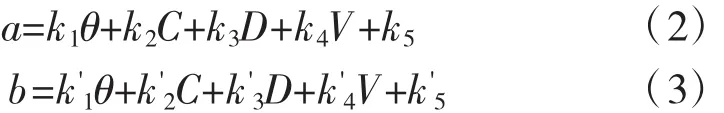
利用最大似然估计法分别对上述参数进行估计，最终得到轨迹模型如式（4）～式（6）所示。由结果R2可知，线性模型对参数a和b拟合效果较好。

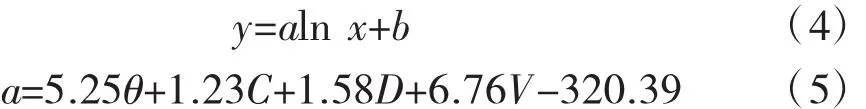
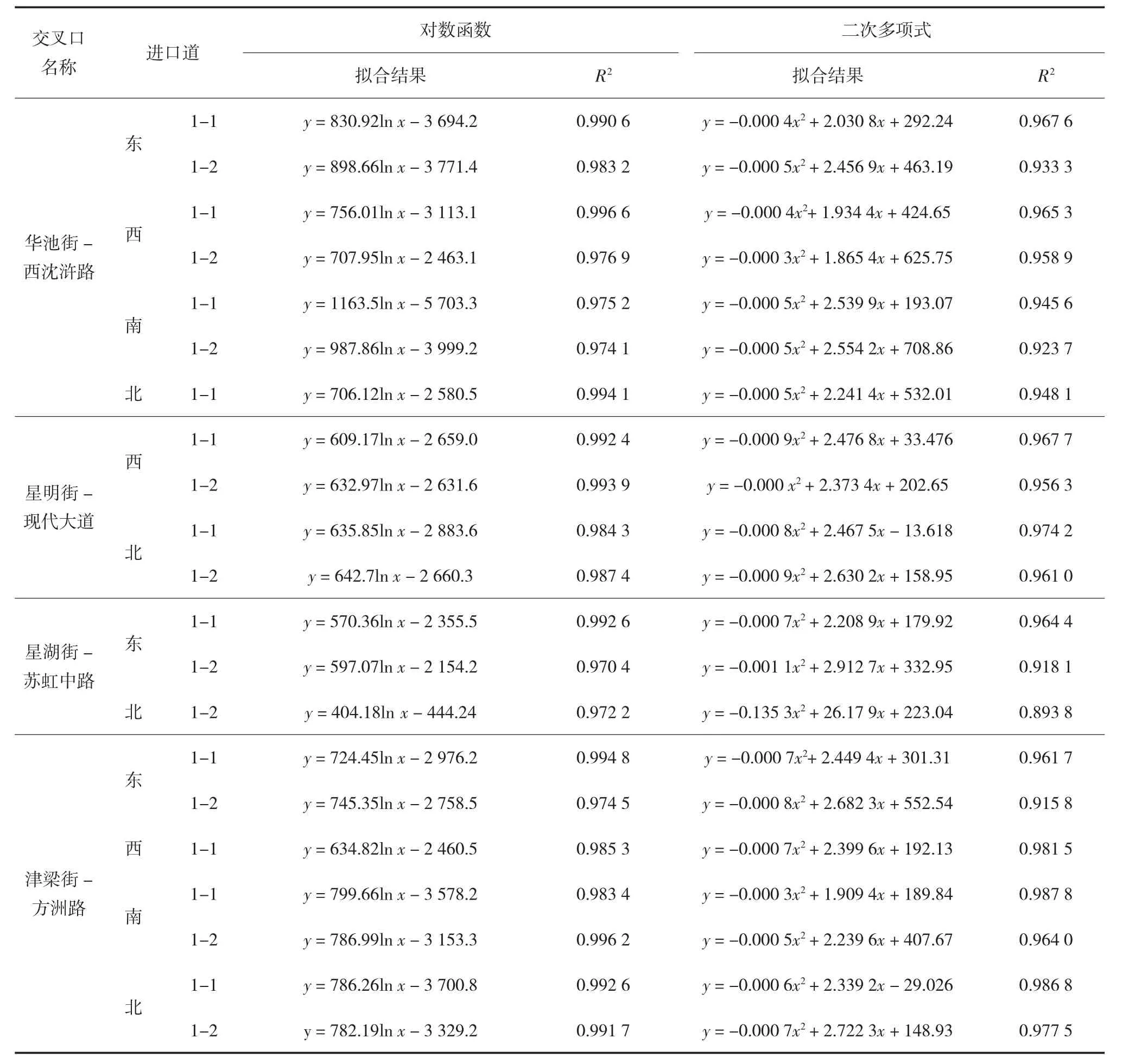
表2 轨迹拟合结果表

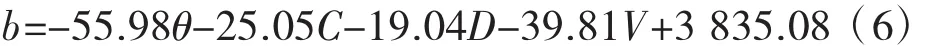
3 实例验证

选择金鸡湖大道-星湖街交叉口的南进口道作为验证地点，确定调查时间为 8：00～9：00，该进口道设有一个右转专用车道，尺寸如下：R=12.21 m；θ=1.585 3 rad；C=22.5 m；D=25.4 m；V=20.35 km/h。假定车辆在验证地点的右转轨迹服从式（4）～式（6），将几何尺寸代入，得到：a=255.26，b=1 888.96。

针对调查交叉口计算平均轨迹，分别使用两种计算方法得到计算轨迹与实际轨迹数据的相对误差。因选取实际轨迹坐标点与计算坐标点横坐标相同，故选择纵坐标值计算误差，轨迹计算值与实际值的对比见图3。由图3可见，利用本文模型计算的轨迹坐标点与实际值的最大相对误差为14.25%，最小相对误差为0.34%，平均相对误差为3.78%，在可接受范围内，因此该模型对无行人、无非机动车干扰下的右转机动车轨迹的预测具有一定的可靠性。

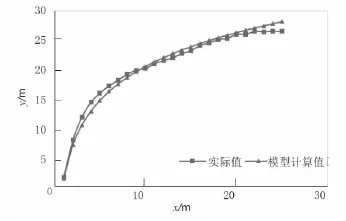
图3 轨迹计算值与实际值对比图

4 结 语

运用视频提取技术，分析了无行人、无非机动车干扰情况下右转机动车轨迹的影响因素，建立了基于几何条件的交叉口右转车辆轨迹模型；运用实测数据对模型的参数进行了标定，并选取实际地点对模型进行了验证。验证结果表明：本文方法预测效果较好，平均预测误差为3.78%，满足精度要求。该模型描述了右转车辆轨迹，可以为仿真技术提供支持，为交叉口平面设计和信号控制提供依据。

由于受软件精度的影响，数据采集的精准性仍需进一步提高，且后续研究中需对有干扰情况下的右转车辆轨迹行为进行分析，建立实用性更强的轨迹模型。