轮毂液压辅助驱动车辆蠕行模式控制研究

曾小华,刘持林,李文远,宋大凤,李立鑫

(吉林大学汽车仿真与控制国家重点实验室,130025,长春)

重型商用车辆的工作环境复杂且恶劣[1],经常需要低速移动,可能会出现整车机械传动系统无法正常工作的极端情况,如变速箱损坏或传动轴断裂等。轮毂液压辅助驱动系统因性能优异,应用于重型商用车辆优势明显,目前已经引起国内外研究学者的重视[2-5]。国内对轮毂液驱系统的研究尚处于起步阶段,例如:哈尔滨工业大学的孙辉等提出了不同结构形式的液压混合动力车辆的控制策略[6-7];吉林大学的曾小华等对轮毂液驱混合动力系统进行了研究[8],提出了轮毂马达驱动的液压闭式系统构型方案[9],并提出了轮速跟随的整体控制思想[10],但对该系统的研究仍有不足,如方案优化与控制等,需要进一步完善[11];吉林大学的李相华等以手柄输入来控制液压泵的排量,但未充分考虑车辆负载的影响[12]。国外企业已经推出应用轮毂液驱系统的相关产品,例如:德国的博世力士乐公司推出了液力牵引辅助系统[13];法国的波克兰公司推出了静液压辅助驱动系统[14-15]。

针对轮毂液驱系统蠕行模式下液压泵排量控制粗放的问题,本文基于轮毂液驱混合动力系统方案,开展了蠕行模式下液压泵排量的控制研究,将蠕行模式下整车传动系统等效为液压机械无级变速器,并将无级变速器的速比控制思想应用于液压泵的排量控制,实现了液压系统根据整车负载自动调节液压泵排量,进而控制发动机工作点实现整车的最佳经济性运行。本研究对液压变量泵排量控制策略的开发及应用应具有一定的借鉴价值。

1 轮毂液驱系统结构

轮毂液驱系统结构如图1所示,基于传统后驱重型车辆结构,添加了液压泵、液压马达、液压阀组等元件。其中,液压泵的输入端通过万向节与发动机后端飞轮处取力器的输出端连接,系统通过调节液压泵组件中主泵的排量来改变轮毂马达的输出功率,以适应不同负载需求。

图1 轮毂液驱系统结构

当重型商用车低速作业或者遇到机械传动系统无法正常工作的极端情况时,可通过发动机带动前轮液压马达提供驱动力,此时轮毂液驱系统工作于蠕行模式。蠕行模式下,整车驱动系统可以简化为以发动机为动力源的变量泵-定量马达系统,如图2所示。

图2 变量泵-定量马达系统

2 蠕行模式控制

2.1 速比特性

当不考虑回路的容积效率时,液压马达的转速与液压泵的排量关系为

(1)

式中:nm为马达转速,r/min;np为泵转速,r/min;Dp=αDp,max,Dp为泵排量(mL/r),Dp,max为最大泵排量(mL/r),α为泵开度;Dm为马达排量,mL/r。式(1)中考虑了系统中存在2个液压马达,下文相关推导也将马达数量考虑在内。

不考虑回路损失时,液压马达的输出转矩为

Tm=ΔpDm

(2)

式中:Δp为马达两腔压差,MPa。

回路中液压马达的输出功率为

Pm=ΔpDmnm=0.5ΔpDpnp

(3)

综上所述,液压泵和液压马达所组成的容积调速回路为恒转矩输出,可实现正反向无级调速,液压马达的输出转矩和回路的工作压力均由负载转矩来决定。液压马达参数如表1所示。

表1 液压马达参数

由液压泵到液压马达,根据速度特性式(1),得到速比为

(4)

由上述分析可知,由液压泵到前轮之间的液压系统,在不考虑损失时,可简化为速比为21.73/α的无级变速器。当系统中取力器速比为108时,发动机到前轮之间的速比为23.49/α。

蠕行模式下,通过调节液压泵开度α,可实现由发动机到驱动轮处最小速比为23.49的无级变速。

2.2 控制方法

根据蠕行模式下车辆的行驶情况,通过调节液压传动系统的速比来改变发动机转速,进而控制发动机工作点,实现车辆的最佳经济性运行。无级变速器的目标速比的计算公式为

(5)

式中:icvt,obj为无级变速器的目标速比;r为车轮半径,m;nopt为发动机最佳经济性运行时对应的转速,r/min;i0为主减速器速比;ua为实际车速,m/s。

将无级变速器的速比控制应用于蠕行模式下液压泵排量的控制,流程如图3所示。加速踏板开度首先转化为需求功率,然后根据需求功率和发动机实际转速控制节气门开度,使发动机输出功率跟随加速踏板开度的变化。通过需求功率与发动机最优曲线确定发动机目标转速,并根据车速、车轮半径、发动机转速与主减速比之间的关系得到目标速比,

图3 蠕行模式的液压泵排量控制流程

进而控制液压泵的排量。

基于以上无级速比控制方法,以驾驶员加速踏板作为输入量,设计车辆蠕行模式的等速巡航控制。等速巡航是指车辆行驶或作业过程中,即使操作员不踩加速踏板,车辆仍可自动保持操作员所希望的行驶速度。若道路坡度或负载阻力发生变化,控制系统可自动调节发动机转速或传动系参数,使车辆按目标车速自动行驶。等速巡航控制可以减轻操作员因长时间控制油门而产生的疲劳,减轻劳动强度,减少或避免事故的发生。

传统比例积分微分(PID)控制器具有原理简单、使用方便、鲁棒性好等优点,但对于非线性、时变性和不确定性大的复杂控制对象,存在参数整定不良、性能欠佳和环境适应性差的问题[16-17]。因而,当采用传统PID控制器进行等速巡航控制时,由于控制参数固定,在外界扰动和路况改变的条件下车速跟随效果较差。模糊PID控制器可以实现PID控制器参数的在线调整,满足对车速的实时控制,原理如图4所示。

e:速度偏差;ec:偏差变化率图4 模糊PID控制器原理

设速度偏差e和偏差变化率ec的模糊子集为

(6)

式中:ZO、S、M、B分别表示零、小、中和大。

考虑该系统工作时车速较低,确定速度偏差e的模糊论域为{0,2,4,6},偏差变化率ec的模糊论域为{0,2,4,6},输入量e和ec的隶属度函数取为三角形函数,如图5所示。

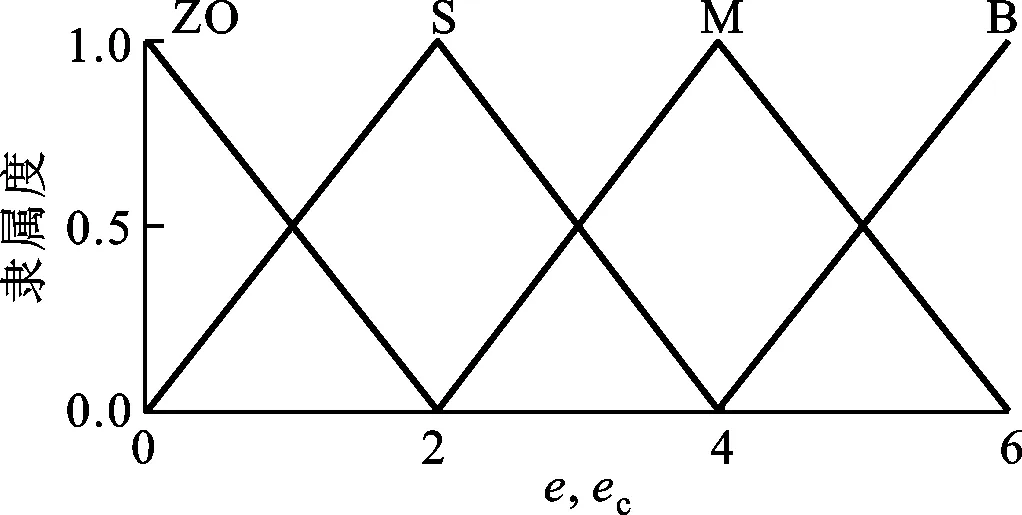
图5 e和ec的隶属度函数

以e和ec作为模糊逻辑控制器的输入量,模糊控制器的输出量为比例系数Kp、积分系数Ki、微分系数Kd[18],分别表示为

(7)

式中k为取样次数。由整定公式(7)知,下一步控制器的参数由当前的控制器参数与模糊推理得出的修正控制参数得到。

当速度偏差e较大时,为尽快减少偏差量,可适当增大比例份额,将积分系数Ki和微分系数Kd尽量调小,甚至作归零处理;当速度偏差e一般时,为保证控制的高精度和系统的响应效果,应适当增大微分系数Kd;当速度偏差e较小时,可取较大的比例积分系数Kp以保证良好的系统稳定性,取适当的微分系数Kd以避免系统在平衡点处出现振荡。基于e和ec的隶属度函数和上述控制设计经验,得出ΔKp、ΔKi、ΔKd的模糊控制规则,如表2～表4[19-20]所示。

表2 ΔKp的模糊控制规则

表3 ΔKi的模糊控制规则

表4 ΔKd的模糊控制规则

3 模型搭建与仿真分析

3.1 模型搭建

根据本文提出的蠕行模式控制,在AMESim中搭建了整车机械传动模型和液压系统模型,如图6所示。

本文研究基于某企业重型卡车,该车整车模型主要动力部件的仿真参数如表5所示。

k:输入常量;J:旋转载荷;α1:输入路面坡度;v:速度传感器;W:转速传感器;T:温度信号转换器图6 整车模型

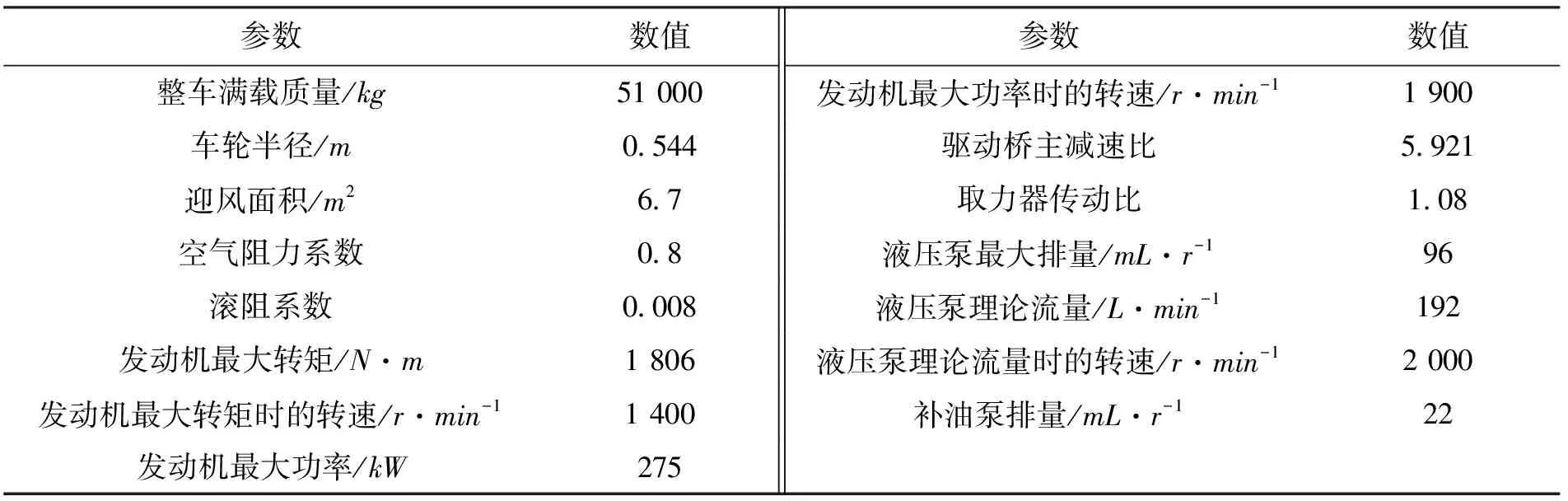
参数数值参数数值整车满载质量/kg51 000发动机最大功率时的转速/r·min-11 900车轮半径/m0.544驱动桥主减速比5.921迎风面积/m26.7取力器传动比1.08空气阻力系数0.8液压泵最大排量/mL·r-196滚阻系数0.008液压泵理论流量/L·min-1192发动机最大转矩/N·m1 806液压泵理论流量时的转速/r·min-12 000发动机最大转矩时的转速/r·min-11 400补油泵排量/mL·r-122发动机最大功率/kW275

3.2 仿真分析

为了检验提出的蠕行模式控制方法的控制效果,设计起步、加速爬坡和等速巡航3种工况进行验证:起步工况可以检验蠕行模式控制方法的响应特性;加速爬坡工况可以在加速踏板和坡度发生变化时,检验该方法的控制效果;等速巡航工况可以检验该方法的自调节能力。

仿真设定的加速踏板开度与需求功率的关系如图7所示。由表1中的马达参数可知,单个马达的最大输出功率为40kW。当加速踏板开度为1.0时,整车需求功率为80kW。为了减小起车时液压系统的油液冲击,在加速踏板开度较小时输出小功率;当加速踏板开度在0.2～0.8区间内,输出功率成比例增加,且增幅较大;此后随着加速踏板开度增加功率增幅减小。该曲线符合机械传动车辆加速踏板开度与需求功率的一般规律。

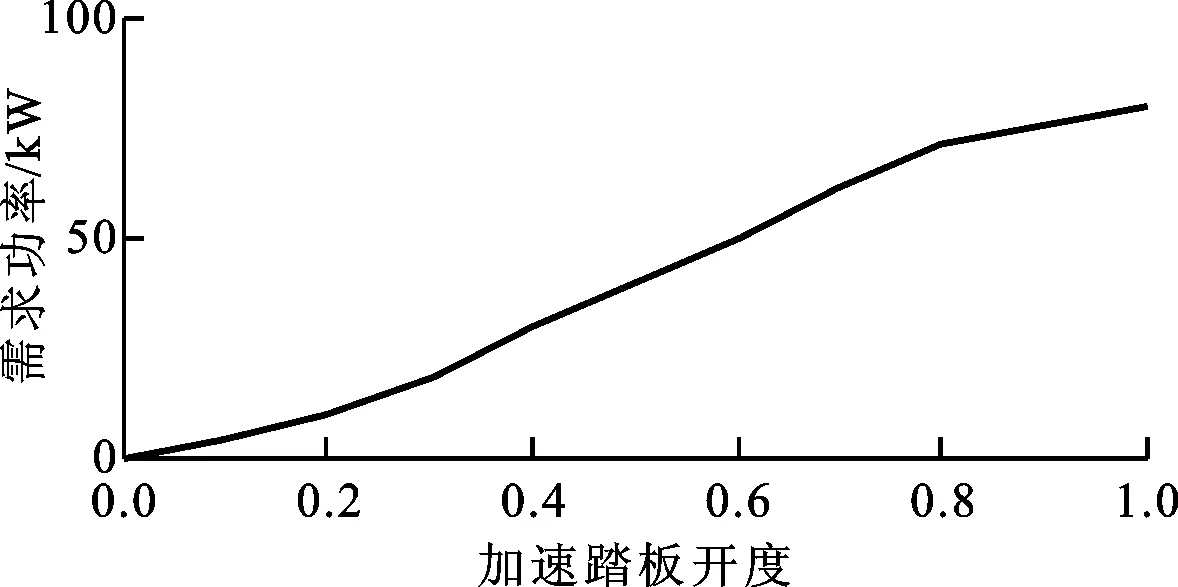
图7 加速踏板开度与需求功率的关系

AMESim发动机模型中发动机转速、发动机功率与节气门开度的关系如图8所示。

图8 节气门开度与发动机转速和功率的关系

3.2.1 起步工况 仿真过程中加速踏板开度随时间t的变化如图9所示,10s时踏板开度由0增加到0.4,历时2s。

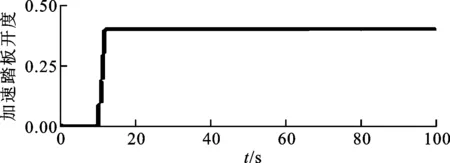
图9 加速踏板开度变化

在起步踩下加速踏板的过程中,车速、目标速比、发动机转速、液压泵开度与时间的关系见图10,可以看出:10～12s,发动机转速增加,此时由于车速较低,目标速比很大;12～17.13s,车速上升,速比降低,液压系统起作用,液压泵开度增加到1.0,车辆在恒定的发动机转速下加速;在17.13s,由于液压系统的限制,速比到达下限23.49;之后,发动机转速和车速持续上升,直到与外界阻力平衡。

(a)车速

(b)目标速比

(c)发动机转速

(d)液压泵开度图10 起步工况仿真结果

由图10可以看出,在10～17.13s,提出的蠕行模式控制方法可以实现速比大于23.49的无级变速,此时液压系统调节发动机工作于高效率区间。但由于液压系统限制,在17.13s以后,速比低于系统控制下限23.49,发动机转速逐渐升高至最高1 900r/min,车速也随之升高至蠕行模式的最高车速4.61m/s。在液压系统起作用阶段,液压机械无级变速器的速比控制效果明显。

当液压泵开度为1.0时,发动机转速达到最大值1 900r/min,速比达到最小值23.49,液压马达转速达到最大值80.95r/min,蠕行模式下的最高车速为4.61m/s。若只考虑滚动阻力和空气阻力,此时的需求功率只有4.93kW,参考图7,该需求功率对应的踏板开度为0.13,故本仿真条件设定的踏板开度0.4明显偏大。

3.2.2 加速爬坡工况 仿真的加速爬坡工况如图11所示:10s时,加速踏板开度由0增加到0.4,历时2s;100s时,输入路面坡度4%;200s时,加速踏板开度由0.4上升到0.6,历时1s。

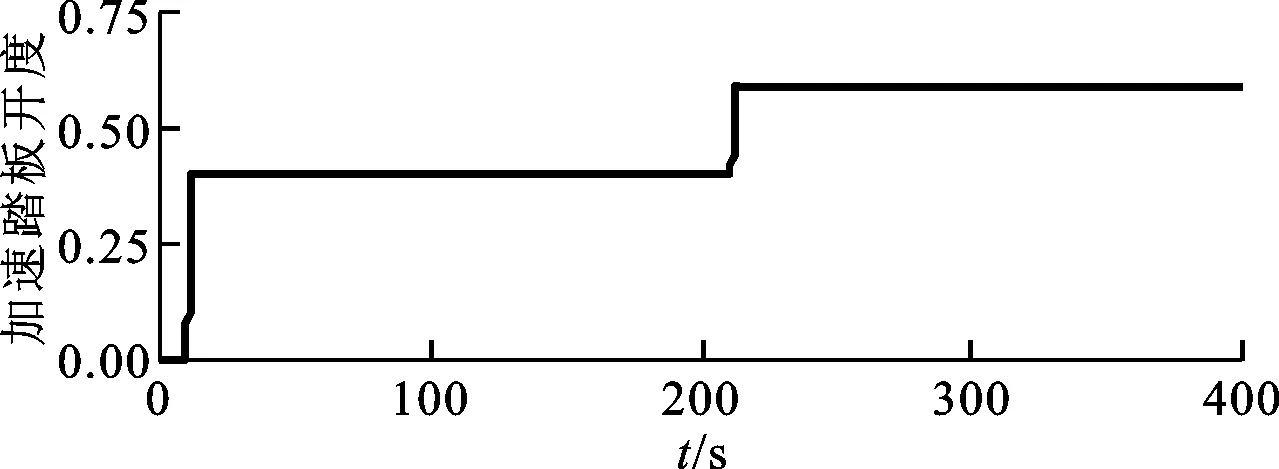
(a)加速踏板开度变化

(b)坡度变化图11 仿真的加速爬坡工况

加速爬坡工况下,车速、目标速比、发动机转速、液压泵开度与时间的关系如图12所示,可以看出:在路面坡度变化之前(0～100s),液压系统响应与起步工况仿真结果相同,整车以蠕行模式下最高车速匀速行驶,目标速比保持恒定;在加速踏板踩下前(100～200s),由于坡度的增加,整车需求功率增加,车速降低,目标速比超过液压系统速比调节下限23.49,液压系统开始起作用,通过改变发动机转速控制发动机工作点,实现车辆的最佳经济性运行;加速踏板踩下后(200～400s),发动机需求转速上升,目标速比减小,加速过程中车速上升,速比开始向减小的方向调节,直到与外界阻力平衡,此阶段速比没有超出液压系统速比调节界限,在过渡阶段发动机经过短暂的非稳态过程重新工作于高效率区间。

(a)车速

(b)目标速比

(c)发动机转速

(d)液压泵开度图12 加速爬坡工况结果

3.2.3 等速巡航工况 采用传统PID与模糊PID分别进行仿真,对比蠕行模式下等速巡航车速的控制效果。仿真过程中起车(第10s)时,加速踏板开度由0增加到0.4,历时2s,第30s时进入等速巡航,100s时输入路面坡度4%,仿真结果如图13所示。

图13 不同控制方法的车速跟随结果

由图13可知,打开等速巡航开关和改变坡度之后,整车在经历短暂小幅度的非稳态状态后,迅速跟随目标车速,模糊PID控制效果优于传统PID。

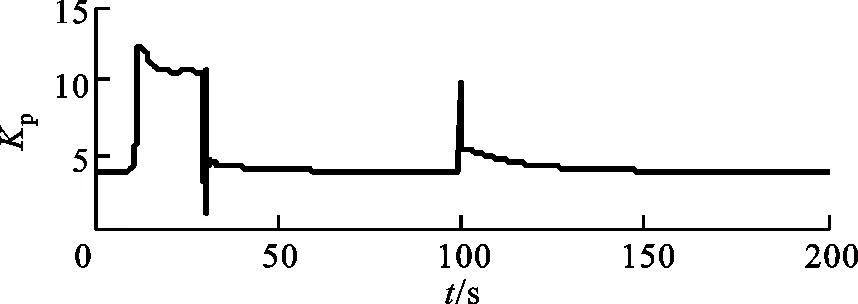
(a)参数Kp的变化

在传统PID控制中,Kp=4,Ki=0.33,在模糊PID控制中,Kp和Ki的变化如图14所示,可以看出,在仿真过程中参数始终在线调整。

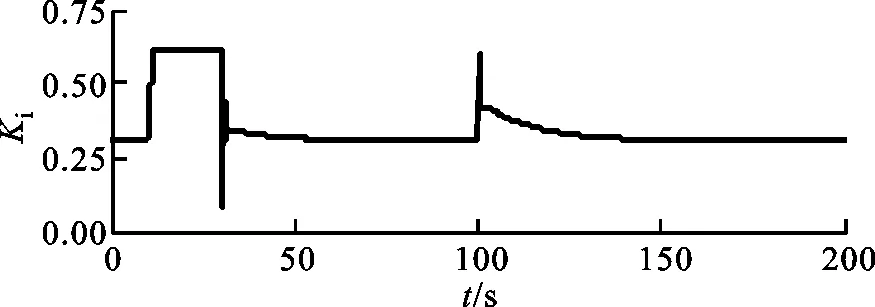
(b)参数Ki的变化图14 参数Kp和Ki的变化

综上可知,提出的蠕行模式控制方法可以满足实际使用要求,通过改变液压系统部件相关参数,可以实现速比在更大范围内进行调节。

4 结 论

针对轮毂液驱系统的蠕行模式,将无级变速器的速比控制思想应用于液压泵的排量控制;利用AMESim软件建立轮毂液驱系统整车模型,并进行实车工况仿真验证。仿真结果表明:在液压系统工作范围内,提出的蠕行模式控制方法可以实现速比的无级控制,通过改变发动机转速调节发动机工作点,实现车辆的最佳经济性运行;此外,基于模糊逻辑的PID控制器能够更加准确地实现蠕行模式的等速巡航控制。