箔片安装位置对气体轴承性能影响的仿真分析

2019-03-08李昊耿海鹏孙岩桦唐思训齐垒虞烈

西安交通大学学报 2019年3期

李昊,耿海鹏,孙岩桦,唐思训,齐垒,虞烈

(西安交通大学机械结构强度与振动国家重点实验室,710049,西安)

对转子系统进行准确的性能仿真预测已经成为现代旋转机械的设计趋势[1]。弹性箔片动压气体轴承是一种柔性表面支承轴承。相比传统油润滑轴承,弹性箔片动压气体轴承避免了高温工况导致的润滑工质恶化,同时,可以省略复杂的供油系统,使系统结构布局更加紧凑[2]。20世纪70年代以来,随着航空航天、核动力、制冷工程技术等对设备要求的不断提高,弹性箔片动压气体轴承得到了广泛的应用,同时学术界对箔片轴承的研究也不断深入[3]。

与滚动轴承及油润滑轴承相比,弹性箔片动压气体轴承由于气体介质黏度低,导致轴承承载力较低,刚度、阻尼偏小,而这对于转子系统整体的稳定性不利[4]。因此,自从弹性箔片动压气体轴承的概念诞生以来,学者们提出了多种结构形式用于提高轴承性能。美国Honeywell公司提出了多叶型箔片轴承,并首次进行试验验证[2]。此后,多悬臂箔片轴承[5]、波箔型箔片轴承[6]、多层波箔型箔片轴承[7]、平箔型箔片轴承[8]、多层鼓泡箔片轴承[9]、压缩弹簧箔片轴承[10]、金属橡胶箔片轴承[11]、稀薄气体润滑轴承[12]等的相关研究相继展开,试验结果表明,这些新结构的弹性箔片动压气体轴承分别拥有提高轴承承载力、改善动态特性、增强稳定性等优点。

在弹性箔片动压气体轴承的箔片周向定位方式上,通常采用点焊或狭槽固定。点焊工艺简单,对轴承座要求低,但在实际运行中,顶层箔片会随着启停次数增多及工作时间的增长发生磨损,底层拱箔会发生松弛甚至压溃,而狭槽固定的安装形式便于更换箔片,因此应用更加广泛[13]。

在弹性箔片动压气体轴承系统试验时,顶层箔片安装狭槽通常布置在轴承座顶部,与转子重力方向相反[14],但并没有相关文献指出这样布置的原因,同时也没有文献指出不同的布置形式会造成什么样的结果。因此,本文将研究顶层箔片安装狭槽的位置对弹性箔片动压气体轴承性能的影响,通过计算分析,得到箔片的安装策略。

1 理论分析

1.1 箔片开口狭槽位置模型

图1为进行理论分析与性能测试时常见的弹性箔片动压气体轴承安装形式,主要由轴承座、顶层箔片和底层拱箔组成[15]。分析可知:顶层箔片通过轴承座上的狭槽实现固定,与轴颈表面形成摩擦副;由于轴颈与轴承间存在偏心距e及偏位角ψ,所以轴颈在以角速度ω旋转的过程中,可以形成动压气体润滑膜,产生的气膜力与转子自重W相平衡,实现支承作用;插入狭槽固定的底层拱箔在气体动压的作用下产生弹性变形,实现柔性支承效果。在进行弹性箔片动压气体轴承装配时,通常将固定箔片的狭槽置于正上方,即图中箔片安装角θ=0°处。

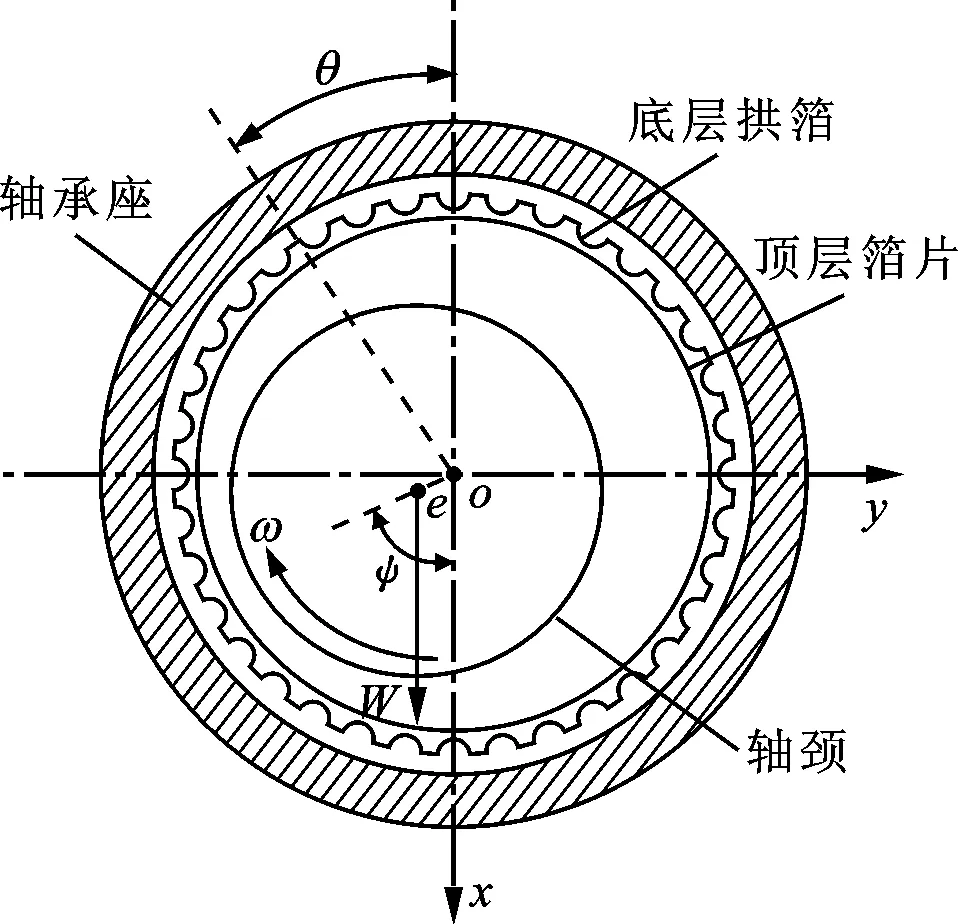
图1 弹性箔片动压气体轴承的安装形式

1.2 控制方程

对于使用常温常压空气润滑介质的弹性箔片动压气体轴承,其润滑情况可以使用理想气体的雷诺方程[15]描述,即

(1)

式中:x和z分别为轴承的周向和轴向长度;h为气膜厚度;μ为气体动力学黏度;ρ为气体密度;p为气膜压力;U为轴颈表面旋转线速度;t为时间。该方程是在广义雷诺方程的基础上忽略表面伸缩效应和挤压效应得到的,这种简化形式在相关研究中得到了广泛的应用[16]。

由于气体具有明显的可压缩性,因此气体轴承中气膜的密度不能再被视为常量,需要特殊考虑。结合理想气体状态方程,可以得到式(1)的量纲一形式为

(2)

归一化规则为

(3)

式中:R为轴承半径;φ为量纲一周向坐标;λ为量纲一轴向坐标;Pa为环境压力,计算中取值为标准大气压;P为量纲一气膜压力;C为名义气膜厚度;τ为量纲一时间;H为量纲一气膜厚度,其描述公式为

H=1+εcos(φ+ψ)+wt

(4)

其中,ε=e/C表示轴颈相对于轴承的偏心率,wt是弹性箔片在气体动压效果下发生弹性变形的量纲一形式,其数学描述[16]为

(5)

其中,α为拱箔柔度,l0为波箔半波纹跨度,ν为底层拱箔材料泊松比,s为单位波纹宽度,E为底层拱箔材料弹性模量,tb为底层拱箔材料厚度,S为拱箔量纲一柔度。

2 数值计算

描述箔片轴承压力分布的方程为非线性方程,无法求出精确的理论解,本文采用有限差分法求解弹性箔片轴承压力分布,差分格式采用二阶中心差分,具体形式不做介绍。给定初始气膜压力及厚度,通过迭代求解即可获得气膜压力及厚度的数值解,进而计算箔片轴承承载力等静态性能。箔片轴承的量纲一承载力计算公式[16]为

(6)

在计算过程中,需要使用箔片弹性变形值不断修正各节点气膜厚度,并使用修正后的气膜厚度进行气膜压力计算,如此反复迭代,直到两次气膜压力计算结果满足收敛要求,其数学描述为

(7)

式中:∑Pi表示第i次迭代所有节点气膜压力的代数和;∑Pi-1表示第i-1次迭代所有节点气膜压力的代数和;δ表示收敛条件,通常取10-5即可满足计算精度要求。

(8)

将扰动方程与雷诺方程联立求解,即可得到箔片轴承的刚度、阻尼系数为

(9)

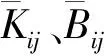
通过上述分析,可以得到箔片轴承的求解流程,如图2所示。

图2 箔片轴承求解流程图

3 仿真结果及分析

为验证本文所述数学模型与计算程序的正确性,使用本文所述模型计算了不考虑箔片安装位置时的轴承特性,并与已有文献进行了对比。表1是使用本文所建立求解模型的计算结果与已有文献给出数据的对比(取宽径比为2.0,轴承数为1.0),对比结果验证了本文所建立求解模型的准确性。

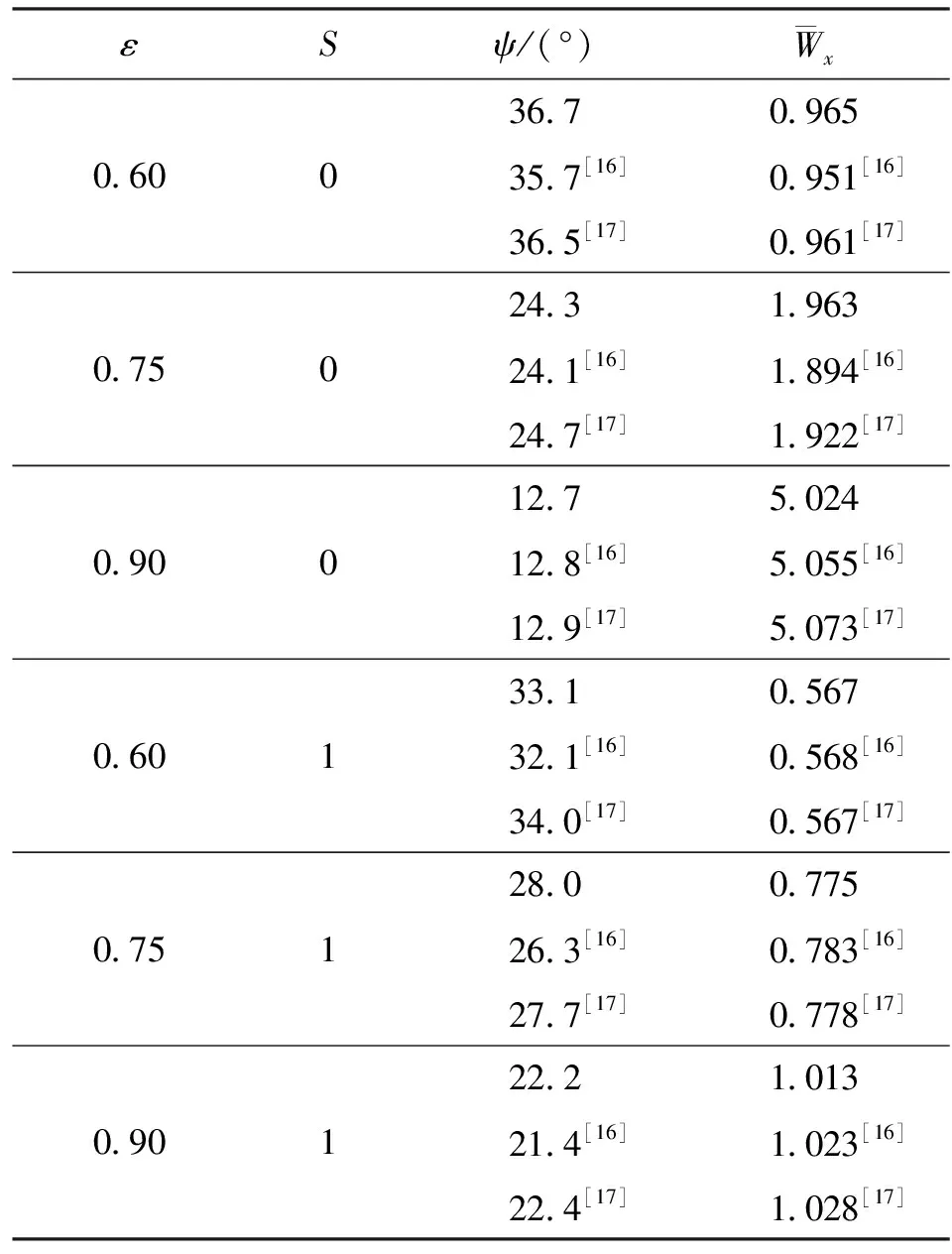
表1 计算结果验证

表2给出了本文分析所用轴承的结构及工作条件基本参数。为方便进行计算,将箔片沿周向剖开为矩形求解域,剖线为图1中箔片正上方,即x轴负半轴。同时,对矩形求解域进行网格划分,周向和轴向的单元数为72×25。

表2 气体轴承基本参数

3.1 承载力分析

图3给出了不同偏心率下,箔片轴承承载力与箔片安装角的关系曲线,可以看出:当狭槽处于某一位置区间时,其具体位置并不会对承载力构成显著影响,相反,当狭槽位置处于“敏感”位置区间时,会非常显著地影响轴承承载力,且偏心率越大,影响越显著;当ε=0.9、θ=170°时,承载力变为最大承载力的32%;当ε=0.3,0.5,0.7,0.9时,对承载力影响最大的箔片安装角分别为155°、158°、162°、170°,而对应偏心率下偏位角的计算结果分别为56°、44°、23°、13°。由此可见,在大载荷条件下(ε=0.7,ε=0.9),箔片最“敏感”安装角与360°整周式箔片计算所得的偏位角近似构成了互补关系,其误差主要是由于本文计算中使用的轴瓦张角为350°。这说明最“敏感”的箔片安装角位于整周式箔片轴承的压力峰值区域附近,因此箔片安装时,安装狭槽应尽量远离这一区域。

图3 轴承承载力与箔片安装角的关系曲线

为研究承载力下降的原因,绘制了ε=0.7时,箔片轴承的气膜厚度与气膜压力在不同箔片安装角下的分布图,如图4和图5所示。从图4可以看出,箔片安装处气膜厚度在数值上远大于其他位置处,不会形成有效气膜压力。因此在计算气膜压力时,该段气膜厚度置空,气膜压力置为环境压力1,如图5所示。从图5可以看出:当箔片安装角处于“敏感”位置区间时,气膜压力分布会发生显著变化,而平均气膜压力的下降会导致轴承承载力的下降。这主要是因为箔片安装位置极大地影响了气膜厚度的分布,而气体轴承的压力分布对气膜厚度非常敏感。相反,当箔片安装角远离“敏感”位置区间时,安装位置角的具体数值并不会对气膜厚度及压力分布构成显著影响,这也说明,在实际安装时,只需保证箔片安装角处于一个位置区间即可,并不需要严格规定具体数值。

(a)θ=0°

(b)θ=120°

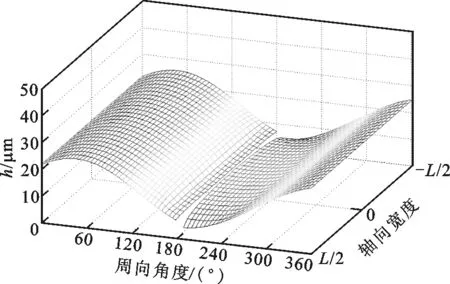
(c)θ=180°

(d)θ=300°图4 箔片轴承气膜厚度分布

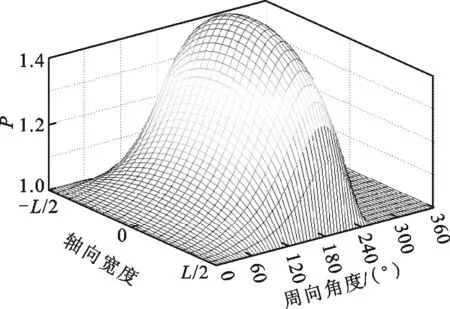
(a)θ=0°

(b)θ=120°

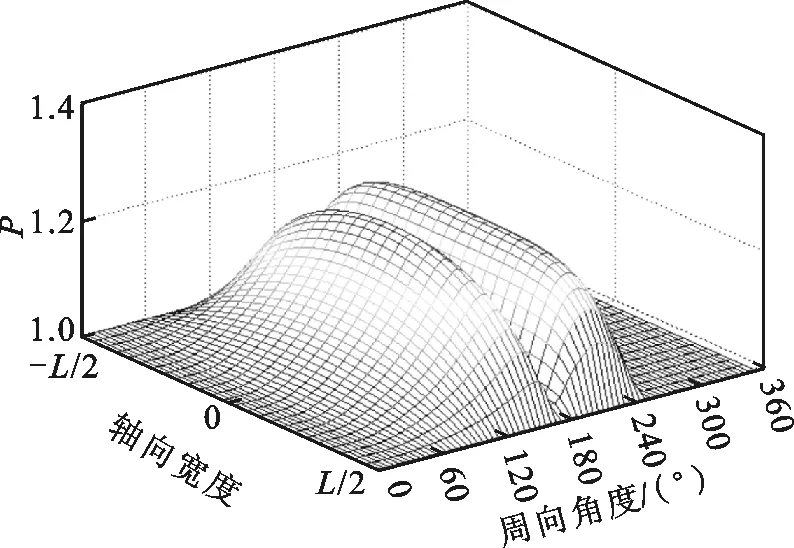
(c)θ=180°

(d)θ=300°图5 箔片轴承气膜压力分布

3.2 动力学特性分析

图6为ε=0.7时,箔片轴承刚度系数与箔片安装位置角的关系曲线,分析可知:当狭槽处于“敏感”位置区间时,箔片轴承的主刚度会显著下降,而交叉刚度会上升,对箔片轴承的稳定工作不利;当狭槽位置处于“敏感”位置区间时,交叉刚度会在数值上非常接近主刚度,意味着轴承的工况已经非常恶劣,微小扰动就可能造成轴承失稳;x方向的最小刚度数值仅为最大刚度的22%,说明箔片的安装位置会极大的影响箔片轴承的稳定性;刚度系数的“敏感”位置区间相比于承载力的“敏感”位置区间提前了约20°～30°,这主要是因为刚度系数对压力梯度的变化更为敏感。