第二十二届北京高中数学知识应用竞赛初赛试题及参考解答
2019-03-08
一、(满分20分)从2018年10月1号我国开始执行的新的个人所得税法,使个人所得税税负水平更趋合理.
(1)小王在北京某高新技术产业工作,税前收入每月15000元.执行新税法之后,小王比原来每月少交多少个人所得税?
(2)有一种速算个税的办法:应税所得额×对应档的税率-对应档的“速算扣除数”.如应税所得额是10000元,它对应的所得税在旧个税方案下是:10000×25%- 1005=1495(元).
请按照这一算法,算出应税所得额是10000元时,在新个人所得税法下对应的所得税是多少?
(3)请计算出表2内的数X,并给出各级“速算扣除数”的递推算法的一般表达式.
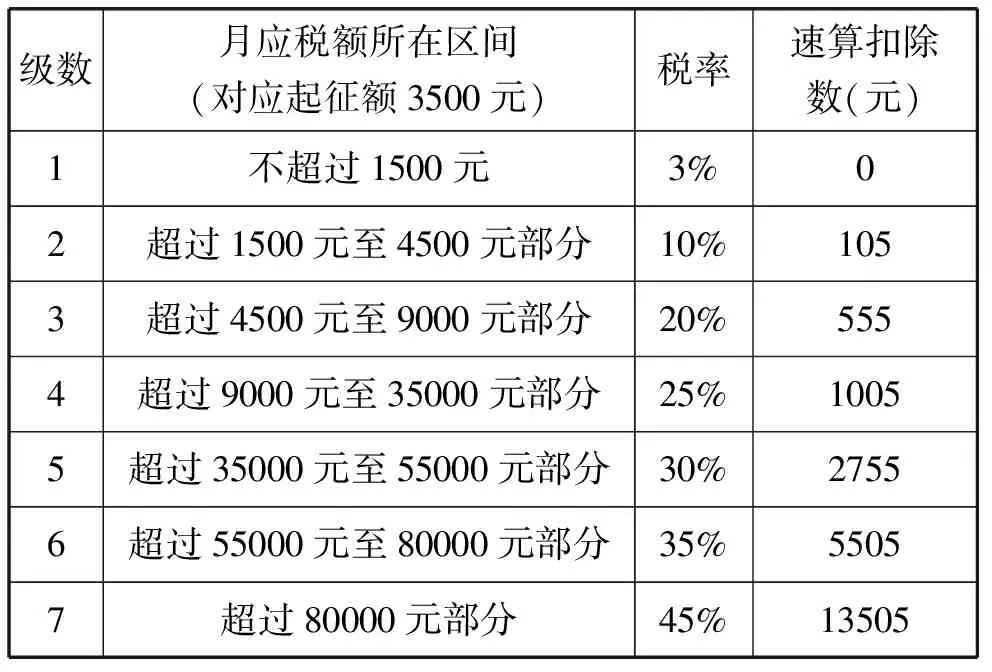
表1 个人所得税税率表(执行至2018年9月30日)
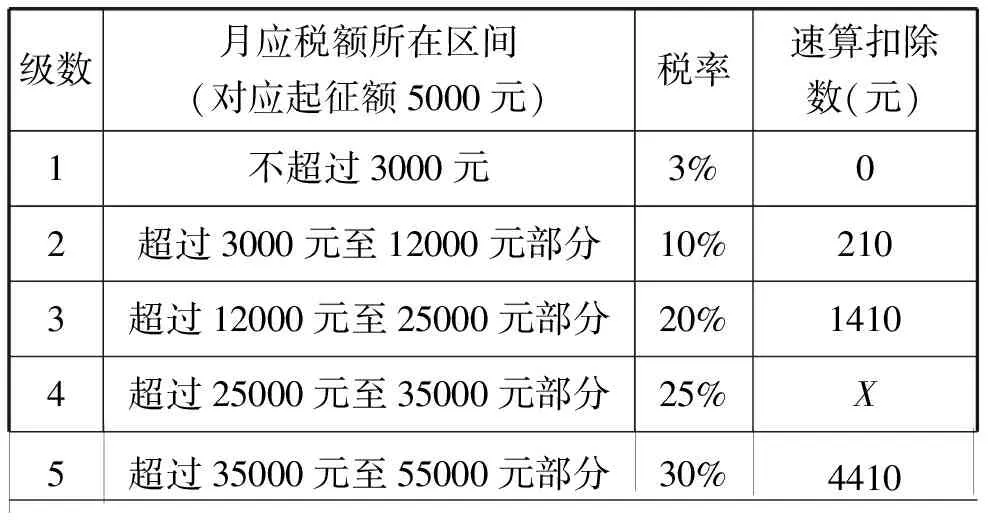
表2 个人所得税税率表(2018年10月1日起试行)
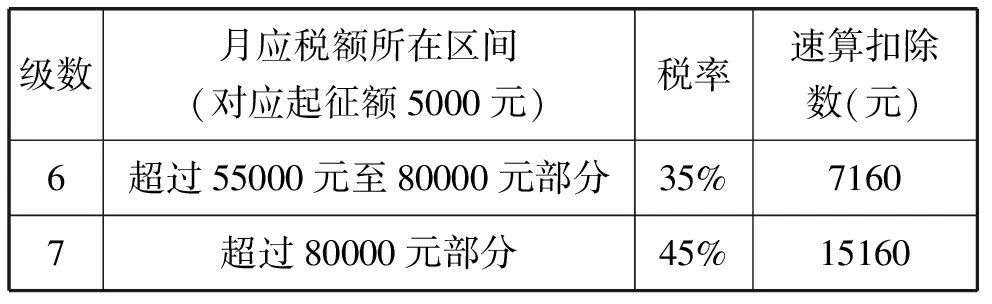
续表
解(1)查阅税法,“五险一金”为不计税所得,假设小王的“五险一金”是3000元.
按旧税法,应税所得额
D旧=15000-3000-3500=8500(元),
将D旧按旧税率表分段,即
8500=1500+3000+4000,
个税上交额
M旧=1500×3%+3000×10%+4000×20%=1145(元);
按新税法,应税所得额
D新=15000-3000-5000=7000(元),
将D新按新税率表分段,即
7000=3000+4000,
个税上交额
M新=3000×3%+4000×10%=490(元),
则有
M新-M旧=490-1145=-655,
即执行新税法之后,小王比原来每月少交个人所得税655元.
(注:若不考虑“五险一金”,所得结论为M新-M旧=790-1870=-1080(元),即执行新税法之后,小王比原来每月少交个人所得税1080元.也算对.)
(2)应税所得额是10000元时,在新个人所得税法下对应的所得税是10000×10%-210=790(元).
(3)由上面的案例可以发现:
本级的“速算扣除数”=上一级最高应纳税所得额×(本级税率-上一级税率)+上一级的“速算扣除数”.
由此可以得到
X= 25000(25% -20%)+1410 =1250+1410=2660(元).
一般推导如下:设an表示应税额依次分段的端点,rn表示应税额区间(an,an+1)对应的所得税率,bn表示应税额区间(an,an+1)对应的“速算扣除数”,其中n∈{1, 2, 3, 4, 5, 6}.
由表2得到:
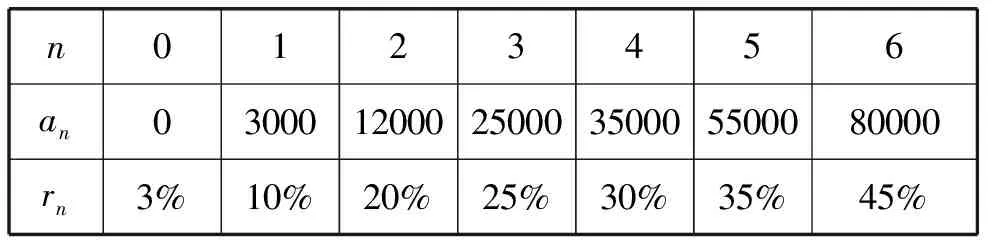
n0123456an030001200025000350005500080000rn3%10%20%25%30%35%45%
设T表示应税额,T∈(an,an+1),Q表示对应应交的个人所得税额,于是
Q=(T-an)rn+[(an-an-1)rn-1+(an-1-an-2)·rn-2+…+(a1-a0)r0]
=T·rn-[(rn-rn-1)an+(rn-1-rn-2)an-1+…+(r1-r0)a1].
定义“速算扣除数”bn=[(rn-rn-1)an+(rn-1-rn-2)an-1+…+(r1-r0)a1],于是得到Q=T·rn-bn,bn=(rn-rn-1)an+bn-1.
由此算出:
b1=(r1-r0)a1=7%×3000=210(元),
b2=(r2-r1)a2=10%×12000+210=1410(元),
b3=(r3-r2)a3=5%×25000+1410=2660(元),
b4=(r4-r3)a4=5%×35000+2660=4410(元),
b5=(r5-r4)a5=5%×55000+4410=7160(元),
b6=(r6-r5)a6=10%×80000+7160=15160(元).
二、(满分20分)在晴空万里,蓝天白云的天气下,也许你看到的是“假蓝天”,原因是臭氧(O3)污染.城市近地层臭氧是典型的二次污染物,主要是由人类活动排放的挥发性有机物、氮氧化物和一氧化碳在太阳光的作用下经过一系列复杂的光化学反应生成的,其带来的温室效应影响着全球的臭氧浓度变化.空气中少量的臭氧使人有一种“新鲜”的感觉,因为臭氧有杀死某些细菌和微生物的能力,但是过量的臭氧对人体和生物都是有害的.
王同学在网站上浏览北京综合检测值变化时,感觉到臭氧的浓度变化似乎与温度和湿度变化有关.为了研究在不同季节,温度和湿度对臭氧浓度的影响,王同学记下了2018年7月2日(代表盛夏)和2018年11月2日(代表深秋)的数据,见表1和表2.请依此回答下面的问题:
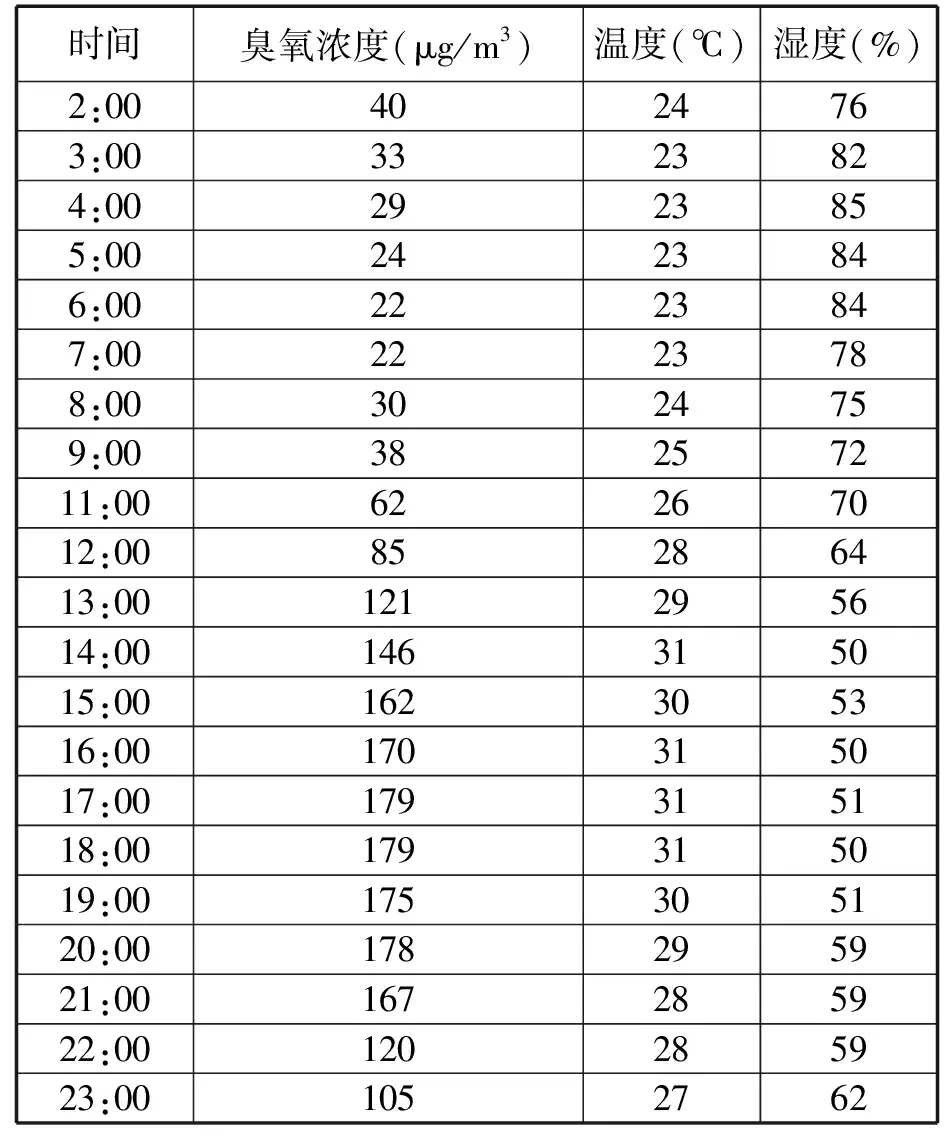
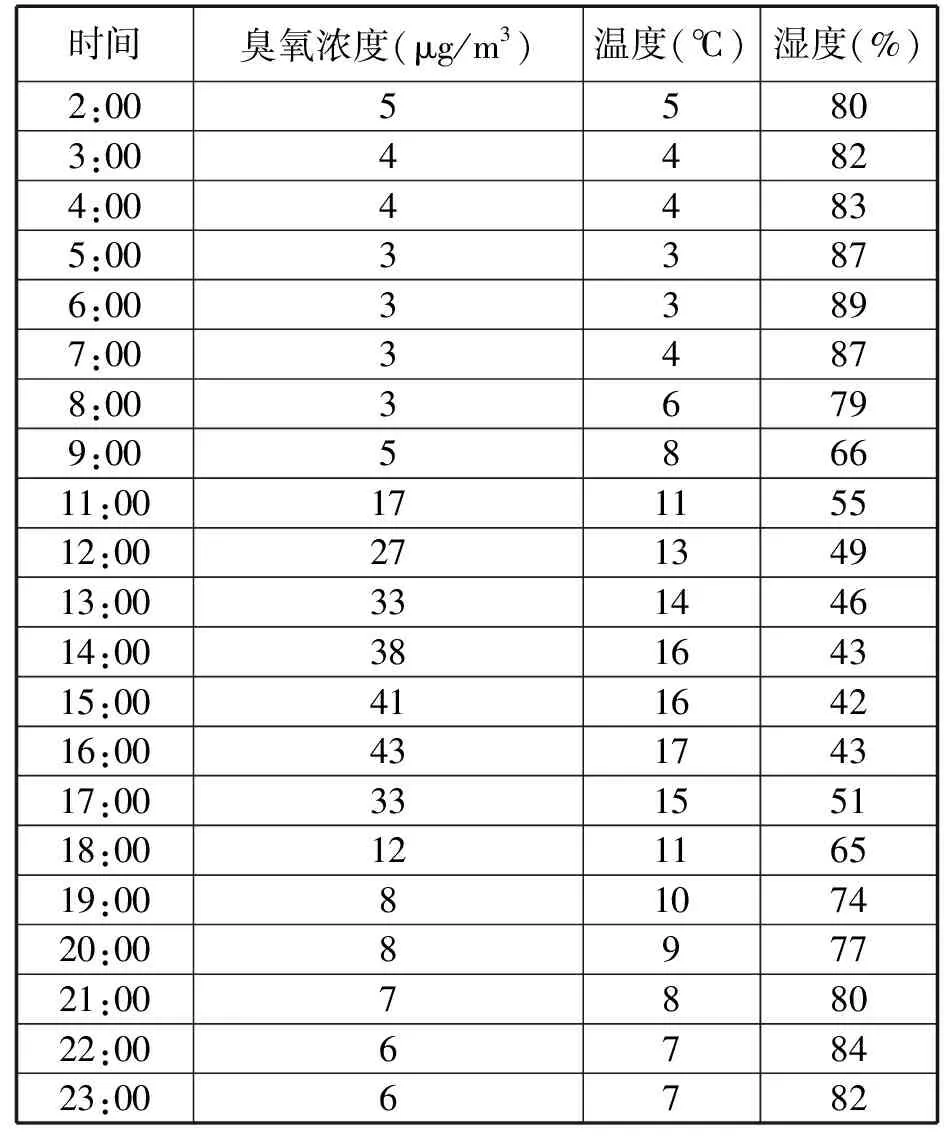
表2 2018年11月2日北京市臭氧浓度变化与温度和湿度变化
(1)分别画出每一天臭氧浓度关于温度变化的散点图和臭氧浓度关于湿度变化的散点图,并分别建立回归方程;
(2)在盛夏和深秋,哪个季节温度变化对臭氧浓度变化的影响大一些? 哪个季节湿度变化对臭氧浓度变化的影响大一些?
解(1)臭氧浓度关于温度、湿度变化的散点图如下:
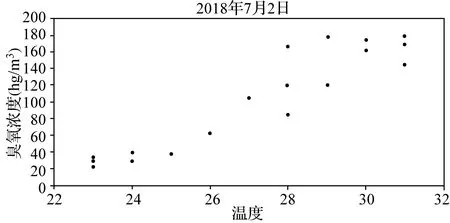
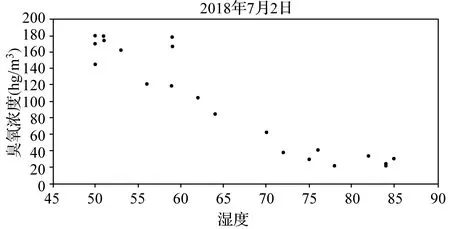
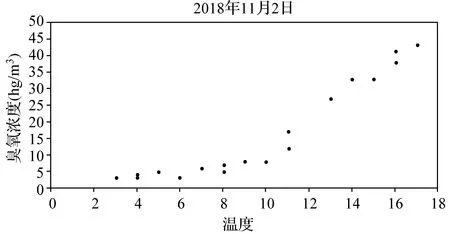
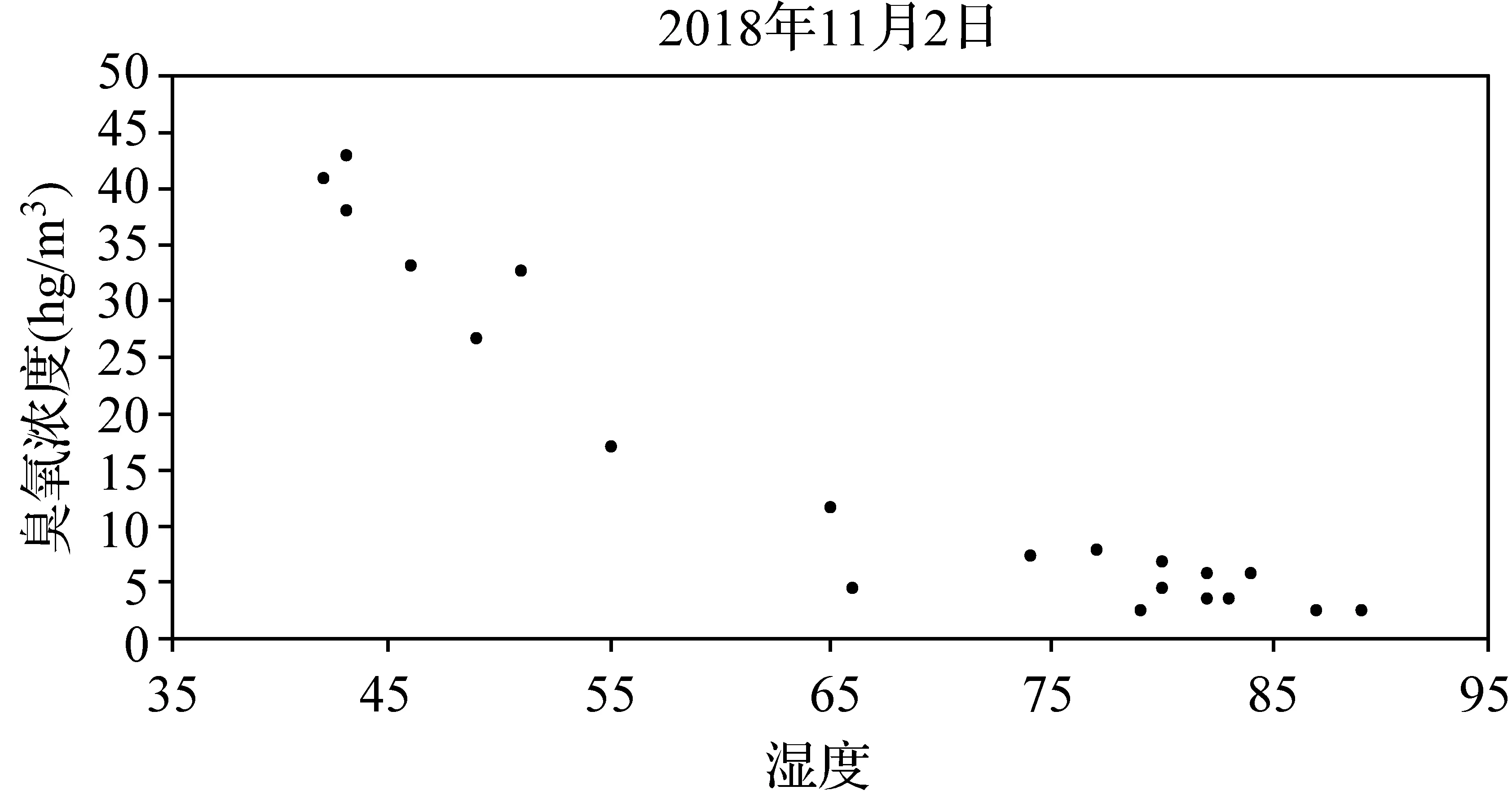
从图中可以看出,四个图的样本点均呈条状分布,臭氧浓度与温度、湿度都有比较好的线性相关关系,因此可以用回归直线y=ax+b来近似刻画它们的关系.计算回归方程的斜率与截距的公式为:
设x1为7月2日北京市的温度,x2为7月2日北京的湿度,x3为11月2日北京市的温度,x4为11月2日北京市的湿度;y1为7月2日北京市的臭氧浓度,y2为11月2日北京市的臭氧浓度.
经计算,
y1= 19.42x1-425.34
(Ⅰ)
y1= -4.72x2+408.34
(Ⅱ)
y2= 2.91x3-11.52
(Ⅲ)
y2= -0.80x4+70.40
(Ⅳ)
(2)2018年7月2日平均臭氧浓度为105.48μg/m3,2018年11月2日平均臭氧浓度为16.48μg/m3.
1° 根据回归方程(Ⅰ)和(Ⅲ),温度每变动1℃,
7月2日的臭氧浓度变化:19.42/105.48×100%=18.41%;
11月2日的臭氧浓度变化:2.91/16.48×100%=17.65%.
2° 根据回归方程(Ⅱ)和(Ⅳ),湿度每变动1%,
7月2日的臭氧浓度变化:4.72/105.48×100%=4.47%;
11月2日的臭氧浓度变化:0.80/16.48×100%=4.85%.
因此,就温度而言,盛夏的温度对臭氧浓度变化影响大一些;就湿度而言,深秋的湿度对臭氧浓度变化影响大一些.
三、(满分20分)将一个8×8的棋盘分割成四个部分,其中两个是梯形,另外两个是三角形,如图1所示.将这四个部分重新拼接,可以得到一个5×13的长方形,多出了一个小正方形,如图2所示.
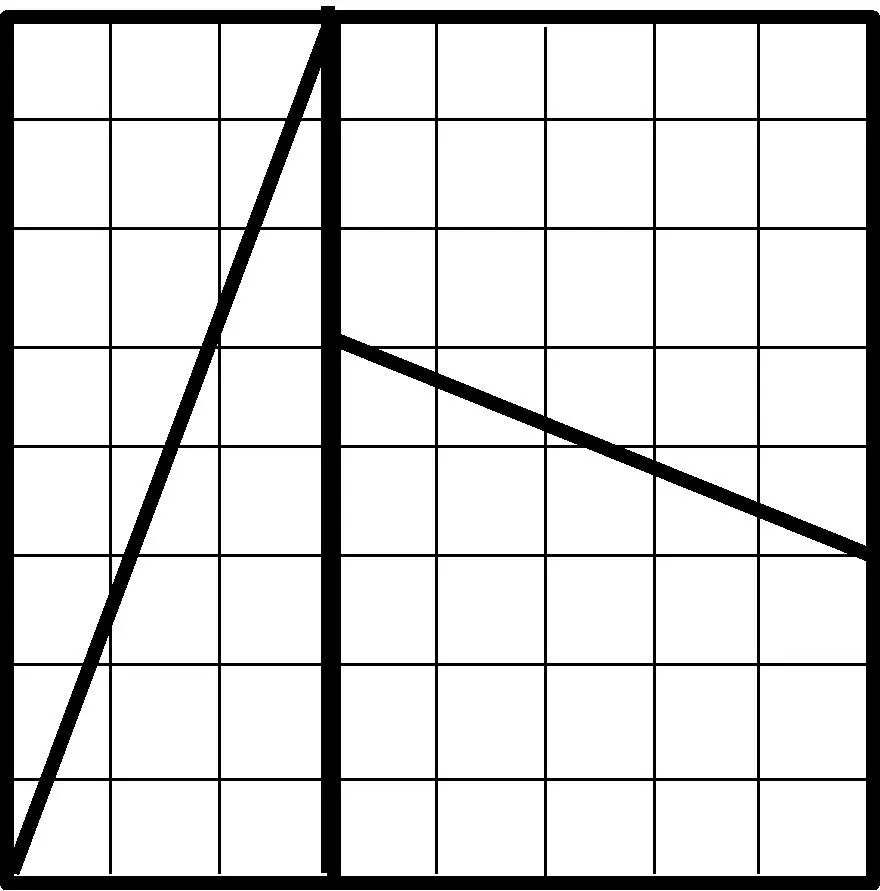
图1
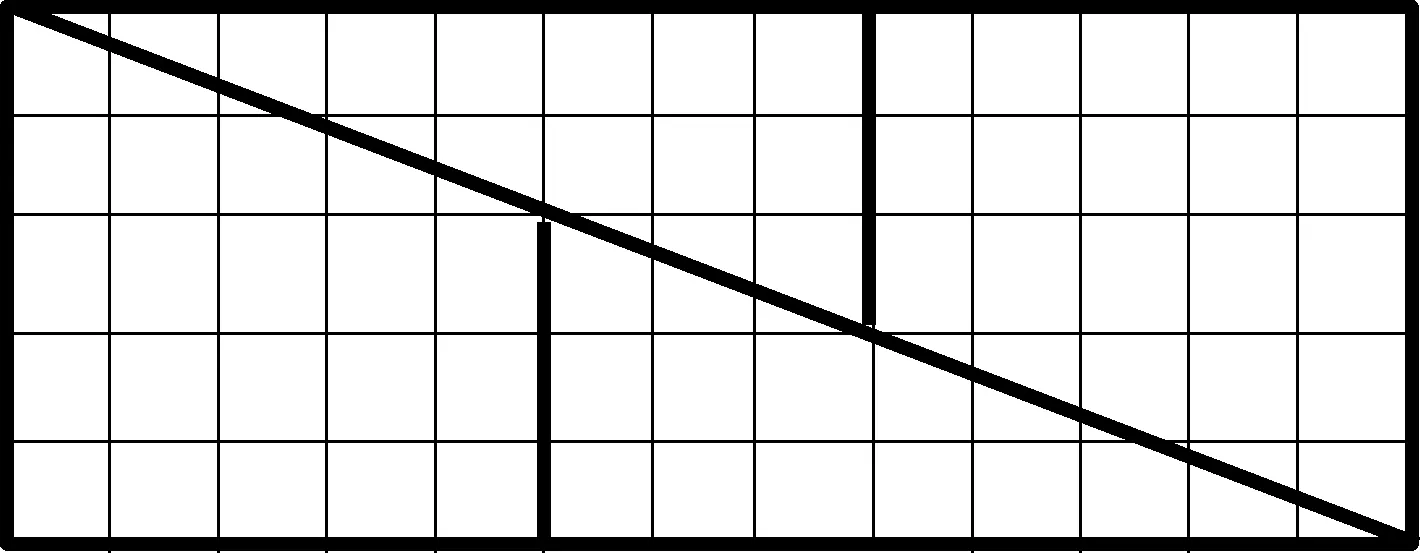
图2
(1)对这种现象你如何解释? 给出解释的数学证明.
(2)对于n×n的正方形棋盘,n取什么正整数时,可以用这种切割重拼的方式得到一个k×m的长方形,使得k×m=n×n+1?举出一个例子.
(3)对于n×n的正方形棋盘,做类似的切割和拼接, 会不会出现k×m的长方形, 使得k×m=n×n-1?如果存在,试给出一般的规律.
解(1)猜测:拼接有缝隙.为了观看清楚,将缝隙夸张地用图4所示,首先证明∠ENG<180°.
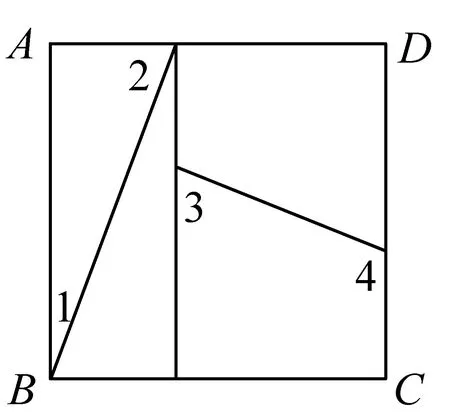
图3
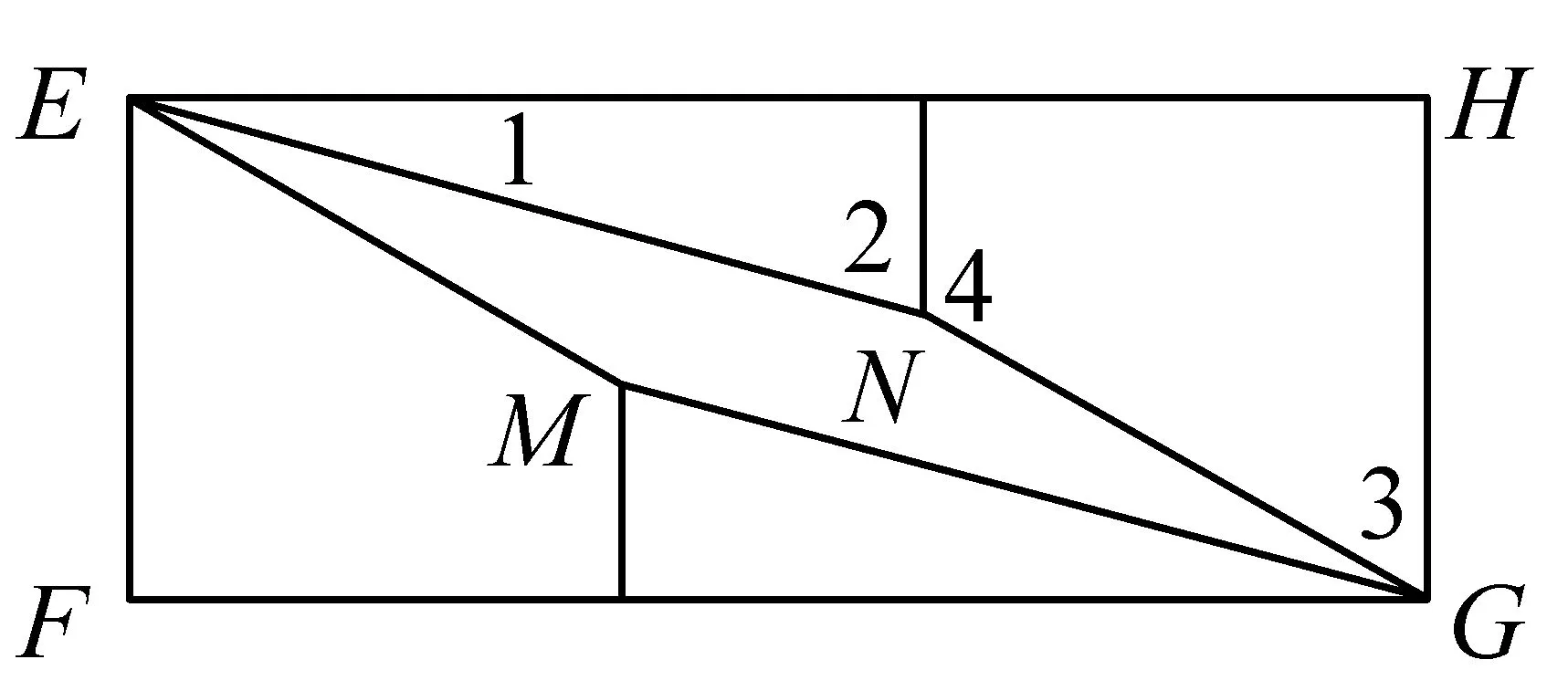
图4
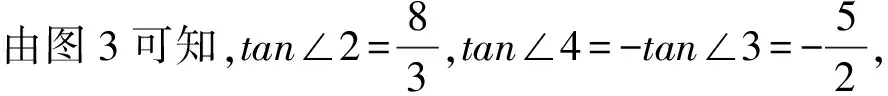
所以∠2+∠4=∠2+180°-∠3=180°+(∠2-∠3)>180°.即∠ENG<180°.易证∠ENG=∠EMG,即四边形EMGN是平行四边形.
SEMGN=|EN|·|NG|·sin∠ENG
=|EN|·|NG|·(-sin(∠2+∠4))
=|EN|·|NG|·(-sin∠2·cos∠4-
cos∠2·sin∠4)
=1.
(2)设分割方式同上,如图5所示,AD边上分割点为P,AP:PD=a:b,则a+b=n.
同(1)的过程,得平行四边形EMGN,令SEMGN=1,即
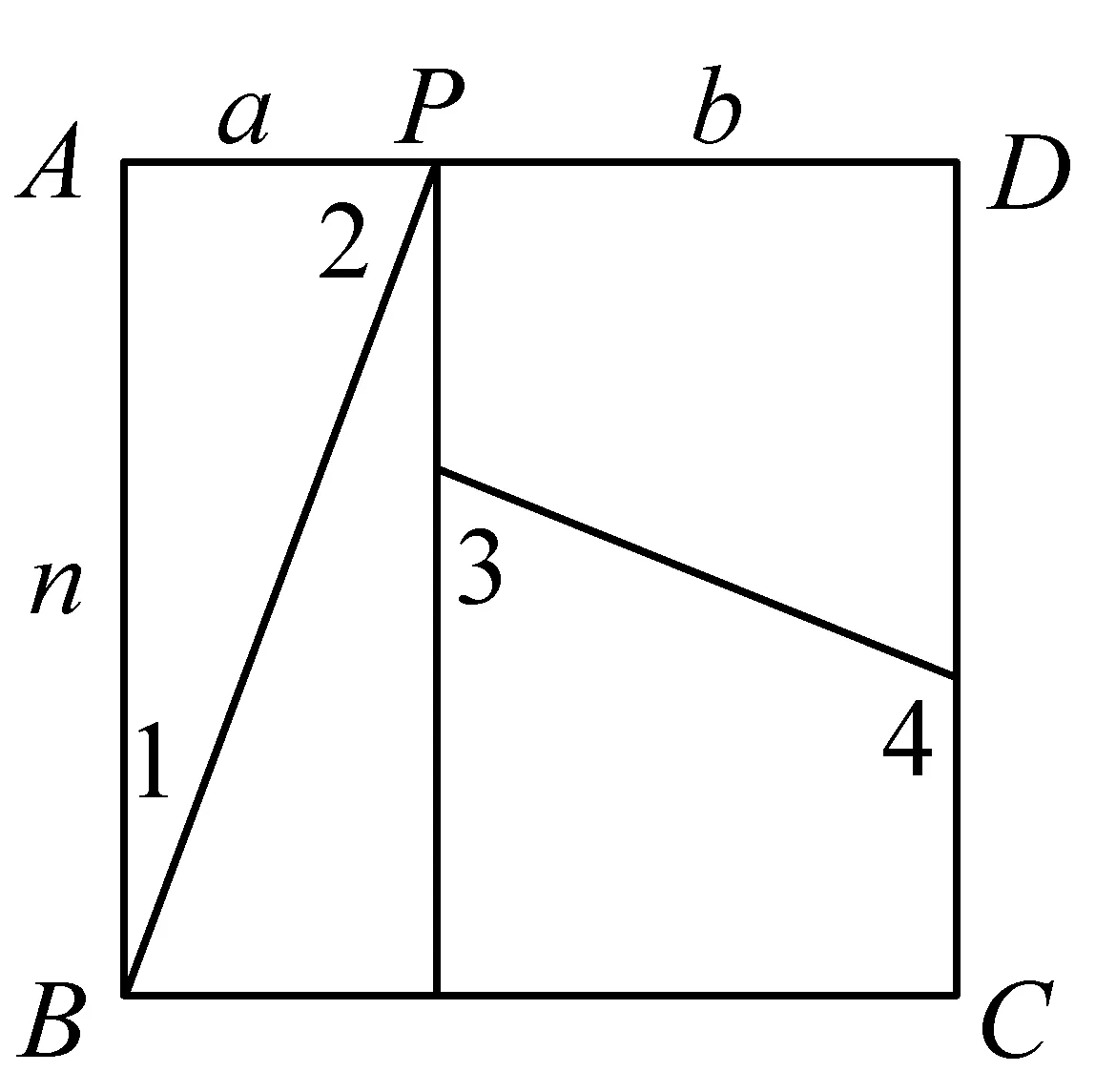
图5
即n(b-a)-ba=1,
即(b+a)(b-a)-ba=1,
即b2-ab -a2-1=0,
显然a≠b, 且 b>a.
枚举得:
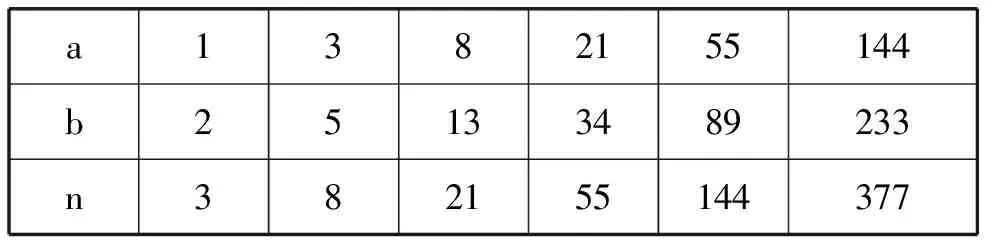
a1382155144b25133489233n382155144377
当n取3, 8, 21, 55, 144, 377, … 时,即n取斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … 从第四项起的偶数项时,边长为n的正方形经过切割,可以再拼接成一个k×m的长方形,使得k×m=n×n +1.
例如55×55的正方形,将55分成21+34,拼成长方形,则正方形的面积为55×55=3025,长方形的面积为(55+34)×34=3026.
事实上,a,b取值依顺序构成从第二项起的斐波那契数列:1, 2, 3, 5, 8, 13, 21, 34, ….
(3)如果n×n的正方形经分割再拼接成k×m的长方形,使得k×m=n×n-1,应该满足以下关系:∠2+∠4<180°,即拼接时会形成重合,重合部分是一个平行四边形ENGM,如图6.令SENGM=1,即
图6
SEMGN=|EN|·|NG|·sin∠ENG
=|EN|·|NG|·sin(∠2+∠4) =1,
即-(b+a)(b-a)+ba=1,
即b2-ab -a2+1=0,
解关于b的一元二次方程得
枚举得:
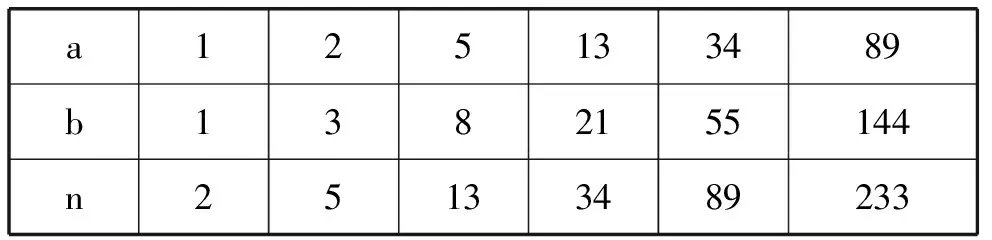
a125133489b1382155144n25133489233
当n取2, 5, 13, 34, 89, 233, … 时,即n取斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … 从第三项起的奇数项时,边长为n的正方形经过切割,可以再拼接成一个k×m的长方形,使得k×m=n×n -1.
四、(满分20分)第19届北京高中数学知识应用竞赛初赛的第五题是关于植物群落更替的生态学问题,情境如下:
云杉芽虫(Choristoneurafumiferana)是云杉林中以云杉树为目标的害虫,它们蚕食树木的新芽、树针和顶芽,严重者能使树干腐烂.虫灾暴发时,害虫会耗尽所有可食的树叶致云杉属的树木落叶致死.云杉树死后代之以山毛榉树(sylvaticaLinnaeus),由于云杉芽虫只食云杉,随着云杉树渐渐死去,大片的山毛榉树成长起来,芽虫也渐渐消失了.没有了天敌,云杉种子得以发芽、成长,凭借在营养与日光上的竞争优势,云杉又渐渐取代了山毛榉.就这样,不同的生物种群世代更替的过程循环不已.
可以用下面的模型来描述这个种群更替的情况.
假设有一个云杉树林,它被划分为许多方格.每个格代表有若干树木生长的空间.指定用“△”表示该空间的云杉树正在被虫害侵害,用“▲”表示该空间云杉树已死并被山毛榉树更替,没有标志表示这里又新长出了绿叶云杉.
假设以“年”为单位描述群落的更替状况.虫害的扩散依下述规则蔓延:
1.被芽虫危害的云杉林地,下一年被山毛榉替代;
2.害云杉的芽虫,下一年转移到四邻(共边的方形)的绿叶云杉林地继续为害;
3.山毛榉林地,下一年被绿叶云杉取代.
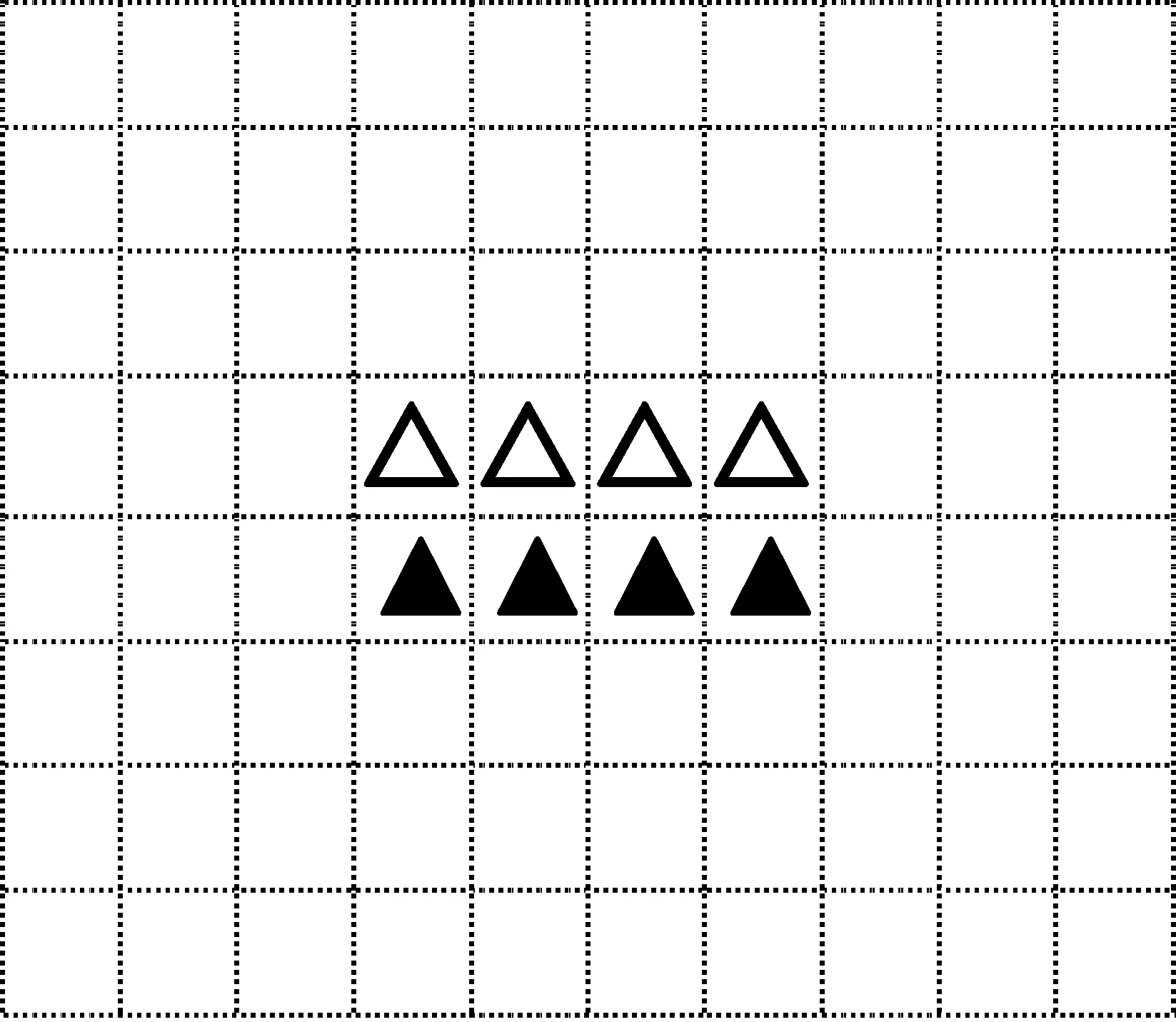
初始的状态为右图,提出的问题(1)是:模拟这个状态经过六年的更替,林地的的格局是什么样?
现在,我们继续考虑这个问题.由于问题只牵涉到云杉,山毛榉和被害虫侵害的云杉这三种群落状态,这个林地被划分为成行成列的状态,我们可以用Zk(i,j)表示在第k年时林地中第i行、第j列的方块地区的群落状态.令Zk(i,j)=0表示第k年时该地块为绿叶云杉林地,Zk(i,j)=1表示第k年时该地块为山毛榉林地,Zk(i,j)=2表示第k年时该地块为被云山蚜虫危害的云杉林地.请回答下列问题:
(1)依据题目给出的相互更替规则,使用Zk(i,j)表示法给出从第k年到第k+1年各方块林地植物群落更替的表达式,即群落更替模型;

(2)根据上述模型,选择一种算法语言,写一个小程序,通过计算机计算初始状态为右图,经过一年、两年、三年更替后这个林区的群落格局.
解(1)群落更替的模型:
如果Zk(i,j)>0,则Zk+1(i,j)=Zk(i,j)-1;
如果Zk(i,j)=0,则
当max{Zk(i-1,j), Zk(i+1,j), Zk(i,j-1), Zk(i,j+1)}=2时,Zk+1(i,j)=2;
当max{Zk(i-1,j), Zk(i+1,j), Zk(i,j-1), Zk(i,j+1)}=0或1时,Zk+1(i,j)=0.
(2)使用上述模型编制的MATLAB计算程序是
>> A0=[zeros(20,20)], A1=A0,
A0(10:11,9:12)=[2,1,2,1;1,2,1,2]
>> For i=2:19
>> For j=2:19
>> B2=[A0(i-1,j), A0(i+1,j),
A0(i,j-1), A0(i,j+1)]
>> if A0(i,j)>0,A1(i,j)=A0(i,j)-1
>> elseif max[B2]=2,
A1(i,j)=A0(i,j)+2
>> elseif max[B2]=0,
A1(i,j)=A0(i,j), end
>> end
>> end
根据此程序的计算,经过一年、两年、三年更替后这个林区的群落格局如下图所示:
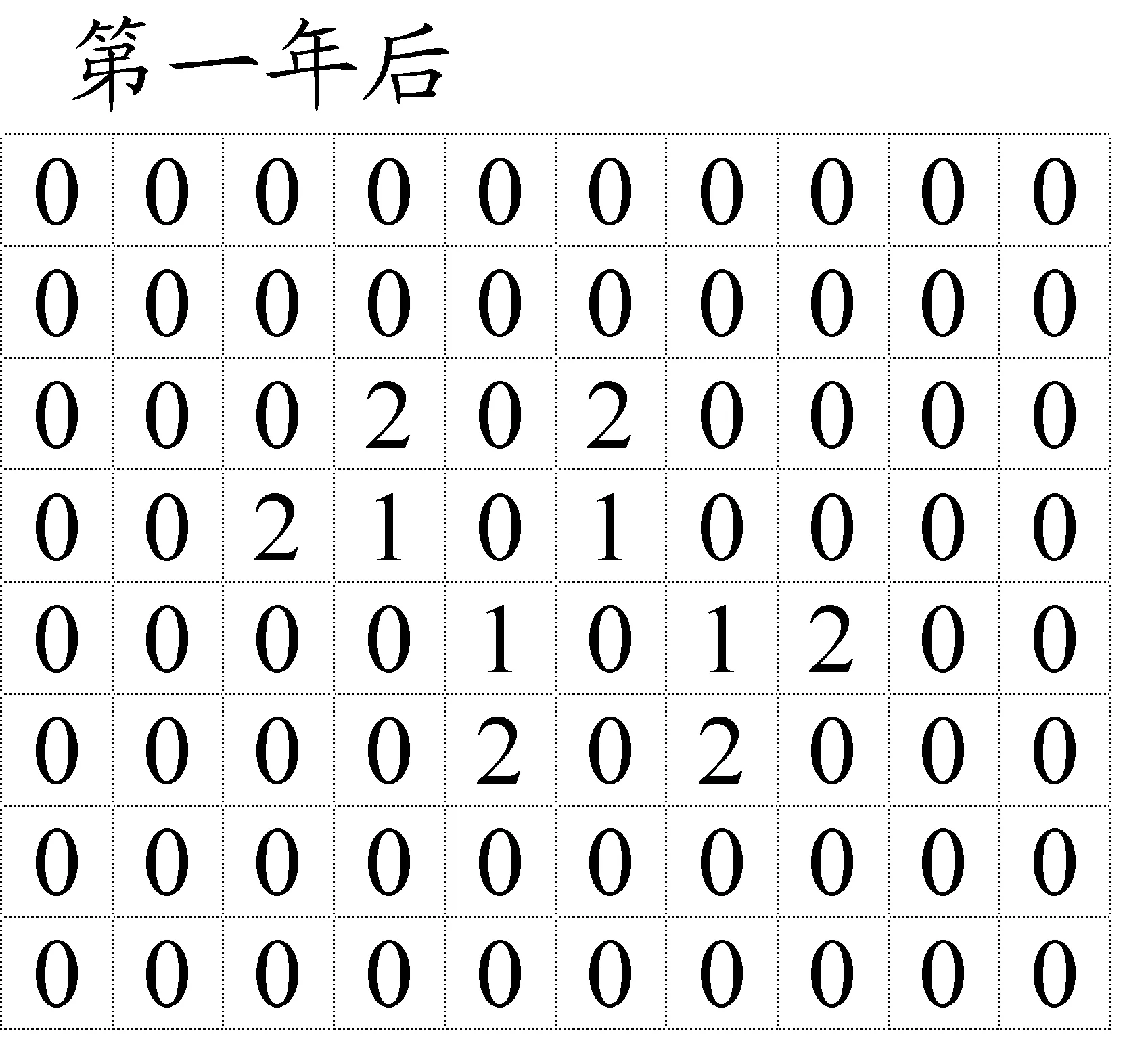
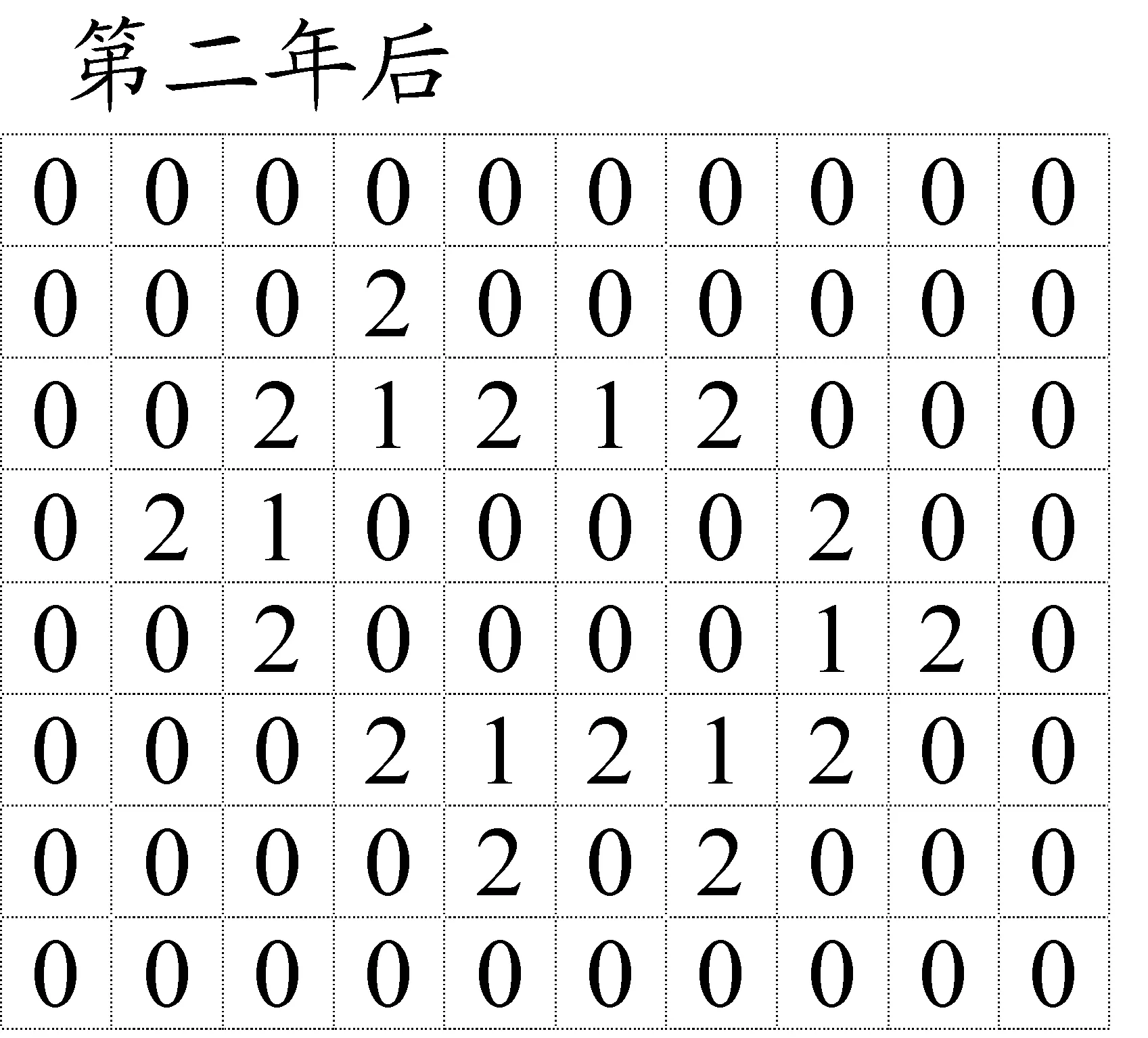
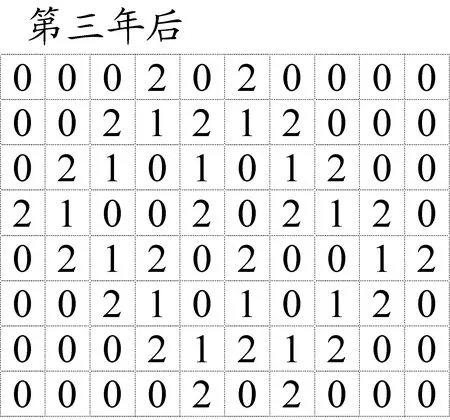
五、(满分20分)中国高铁发展迅速,使有些原本乘飞机到某地出行的旅客改乘高铁了.现在要模拟一次寒假与父母或亲友外出旅行,先选定一个时间,并设定一个既可以乘飞机(经济舱)到达,也可以乘高铁(二等座)到达的目的地.
(1)列出影响选择交通工具的各种因素;
(2)为这次模拟出行选定乘坐交通工具的方案,并说明选择的理由.
解答题要点
(1)影响因素主要有两大方面,一方面是由交通工具产生的,包括乘坐交通工具的时间成本,交通工具的舒适性,安全性,正点率,价格;另一方面是由旅行者产生的,对于不同的旅行者,其价值取向不同,个人感受不同,还有个性化的需求.
(2)要先调查上述影响因素在这次出行中的具体情况,将各种影响因素的情况进行主次排序,或进行量化,在多因素分析中,作出相对优化的选择,形成出行方案.
(注:这个题的解答是很开放的,只要有来自实际的调查分析,逻辑清楚,比较完整,自圆其说,即看作正确.酌情给分,宜粗不宜细.)
