基于插值算法的抽蓄电站振摆分析与运行优化
2019-03-08彭硕群庞希斌王闻震
彭硕群,庞希斌,王闻震
(1.国网新源湖南黑麋峰抽水蓄能有限公司,湖南 长沙410213;2.国网新源华东宜兴抽水蓄能有限公司,江苏 宜兴214200)
1 引言
水轮发电机组作为大型旋转机械,运行中的机组振动是一种普遍存在的、不可完全避免和消除,严重的机组振动现象影响机组的供电质量、安全运行和使用寿命。抽水蓄能电站水头变化大,工况复杂,为满足同期并网要求,相对于常规水电站增设非同步导叶,干扰过流部件内流场的同时加重了水泵水轮机组流场流态紊乱[1]。
为减小水力振动对机组平稳运行的影响,优化机组的运行参数,从而改善其运行状态[2-3],本文针对水泵水轮机运行的关键参数:净水头、有效出力和振摆数值,提出基于Matlab regress函数和interpolant三次多项式函数对离散数据数值仿真,连续的高精度三维图,直观清楚观测某种工况机组的振动情况,通过相对误差结果,验证了该种数学模型拟合原始散点数据建立三维图估测未知工况的方法是可靠有效的,值守人员可以依靠其进行可靠有效的负荷调整[4]。
1 数值仿真与插值
包括单变量、多变量的线性拟合、多项式拟合、高斯拟合等数学模型种类繁多,三维图的精度取决于数学拟合模型的精度,为综合水头、出力两种因素对振摆情况的影响,研究采用多变量线性拟合和多变量插值2种拟合方法,依据MATLAB编程试验平台,输出线性拟合的数学模型和插值拟合的三维仿真图结果,随机选取9组实际运行中的记录数据,根据两种数学模型估测出的振摆数据并比较其相对误差大小,来评价2种数学模型拟合优良程度,并通过相对误差结果验证采用数学模型拟合原始散点数据建立三维图估测未知工况的方法是否可靠有效[5]。
数据来源于黑麋峰抽水蓄能电站实际工况采集数据,具体为1号机组180 MW、250 MW及300 MW左右发电负荷且净水头变化过程中上导轴承、下导/推力组合轴承、水导轴承及顶盖等部位的振摆数据。
2 数据分析
2.1 上导摆度分析
依据上导轴承在变水头、多种出力情况下的68组X向摆度数据,进行曲线拟合,散点数据分布情况如图1所示,总体保持在200 μm左右,随出力变化幅度小,随净水头升高呈现下降趋势,初步判定存在个别异常数据。
多变量线性拟合主要采用MATLAB平台中regress函数,输出结果如下:
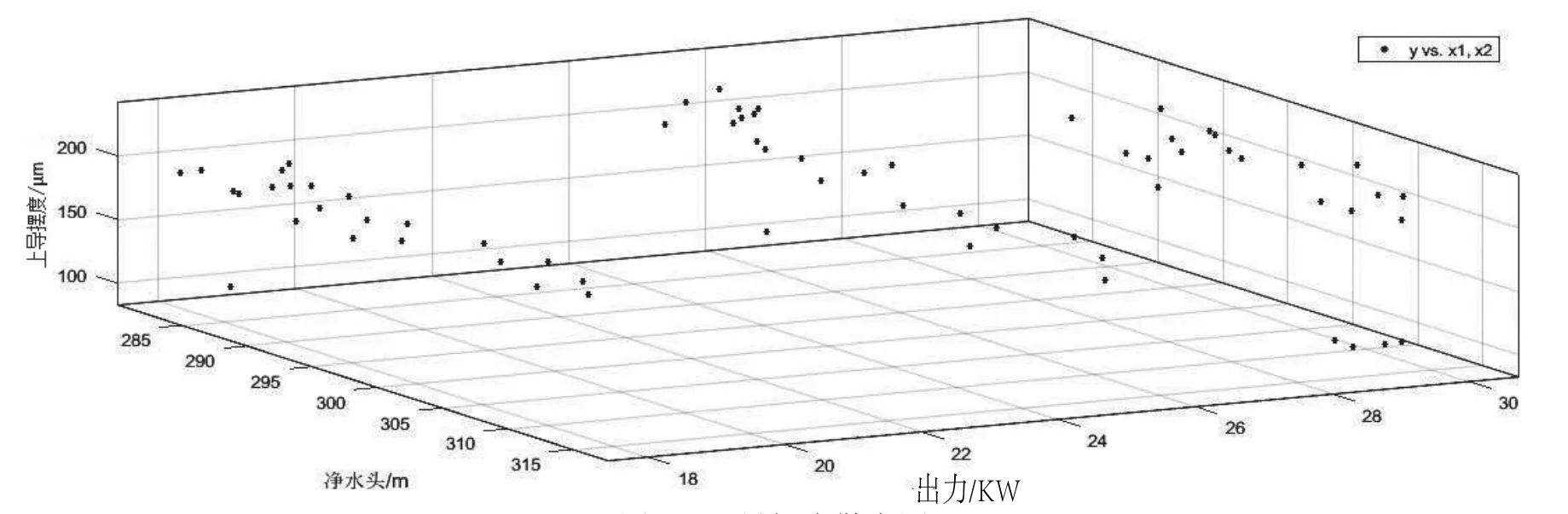
图1 上导摆度散点图
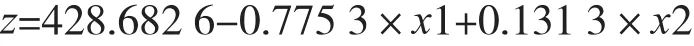
其中z:表示上导摆度,单位μm;
x1:表示净水头,单位m;
x2:表示出力,单位万kW。
根据线性函数的正相关、负相关特性,从数据统计分析角度可以得出以下结论,在净水头和出力的综合影响下,上导摆度受净水头的影响更为严重,且呈负相关关系,即净水头越高,发电工况下上导摆度越小;上导摆度与出力呈正相关关系,出力越大,摆度有平缓上升趋势,且净水头影响因子0.7753远大于出力影响因子0.1313,上导摆度受净水头影响更严重,这与常规水电站有着显著的区别。
插值逼近主要利用MATLAB平台中interpolant函数中的cubic三次多项式函数,仿真输出三维图如图2所示,介于多变量的多项式表示的复杂性和软件的局限性,分析结果未有数学表达式,仅提供可读取数据的三维图。图中深色区域代表相对低摆度区域,明亮的浅灰色代表相对高摆度区域,中灰色代表高摆度与低摆度之前的过渡区域,此区间是值守运行人员在现有报警系统下,较少关注的情况,由此图中过渡区域所占面积可以发现,黑麋峰电站1号机组绝大部分情况处在良好的稳定运行区间,尤其是高水头且高出力工况下,机组上导摆度状况相对最稳定,这与实际统计数据和抽水蓄能电站运行原理是相符合的,三维空间显示效果立体,颜色的强烈对比直观明了,从视觉的角度出发,三维图展示摆度情况效果优良,具有采用价值。
线性拟合能够提供净水头和出力两种因素对上导摆度影响程度,并且以数值形式客观表示,避开了主观缺点;多项式差值能够提供便于视觉观察的三维图,为了对比2种方法的准确性,随机选取68组数据中的9组数据,线性拟合根据输出的线性函数估算,多项式拟合通过读取三维图数据估算,读取方式如图3所示。2种估算结果与真实上导摆度数据对比,估算数据和相对误差统计如表1。结果显示,多项式拟合相对误差在0.20%~1.05%之间,线性拟合相对误差在1.35%~9.74%之间,两者的相对误差均较小,说明通过这2种方式得出的结论均是可靠的,且其中多项式拟合结果相对误差小于线性拟合误差,对于未知工况预测结果将具有更高的可信度。利用该种方式,实现了数据的有效利用和延伸,为前台运维人员值守观测振摆系统提供一种可靠的辅助手段。
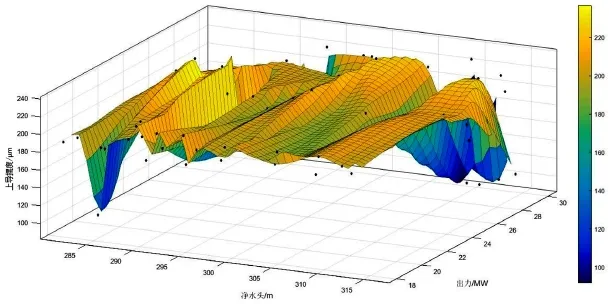
图2 上导多项式插值拟合结果
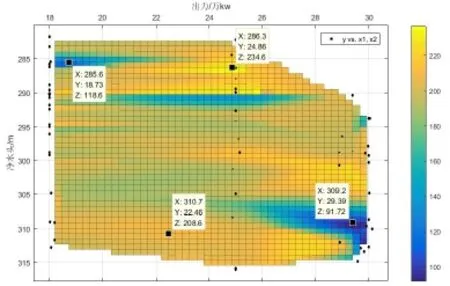
图3 上导多项式拟合数据估测
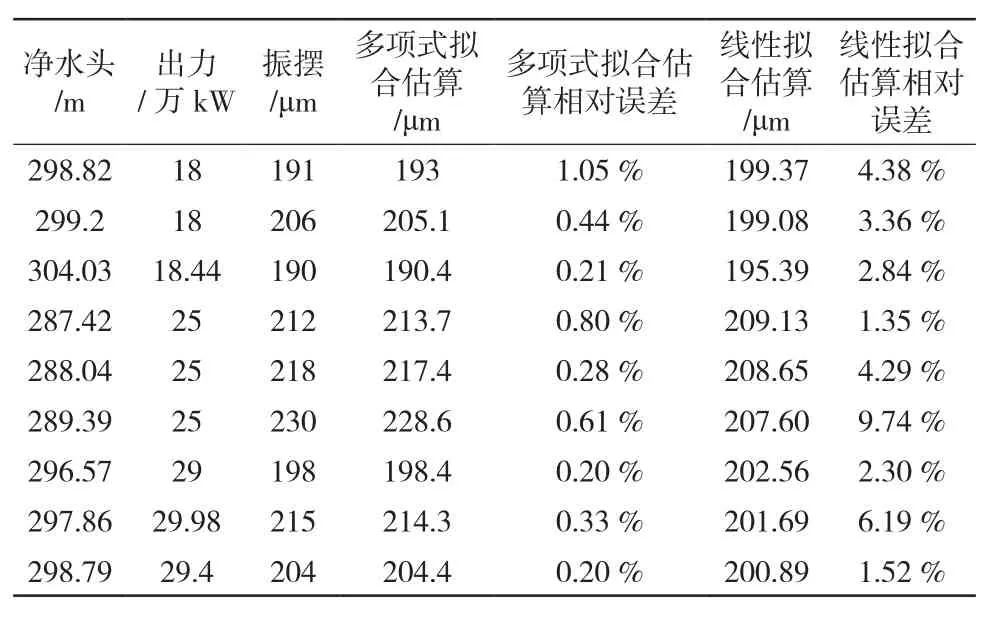
表1 上导摆度线性与多项式拟合对比结果
2.2 推导摆度分析
多项式拟合与真实推导摆度数据对比,估算数据和相对误差统计如表2。结果显示,多项式拟合相对误差在8.46%~0.57%之间,由于数据点分布阶跃状态,使线性拟合相对误差比较大,不具备数据预测功能。其中多项式拟合结果相对误差范围大于上导模型相对误差范围,根据最高误差出现点,说明数据突变点需要进一步补充间隔数据,才能使得估测数据更完善,此处发现对后续完善工作提出了指导方向,即多项式估测模型将在更多更详尽的现场数据点的补充条件下具备更准确的效果。
2.3 水导摆度分析
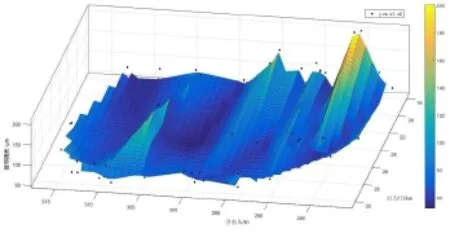
图4 推导多项式插值拟合结果
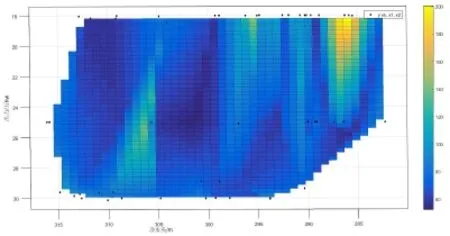
图5 推导多项式拟合数据估测
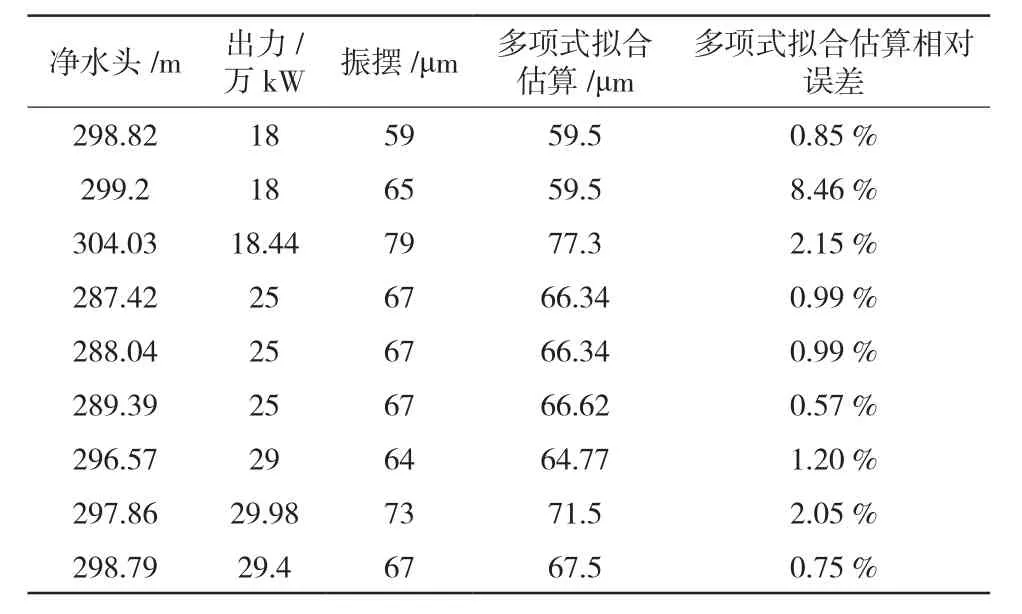
表2 推导摆度多项式拟合相对误差
多项式拟合与真实水导摆度数据对比,估算数据和相对误差统计如表3。水导轴承和上导轴承、推导轴承相比,水导摆度趋势受水头影响比较大,在高水头区域,水导摆度情况良好,几乎不受净水头影响。具体参数输出结果如下,出力对水导摆度的影响因数-10.64和净水头对水导摆度的影响因数0.0254相比较发现,水导摆度受到出力的绝对影响,且出力越大,水导摆度越小;理论上水导和上导、推导做出位置相比,更靠近机组转轮,受到机组出力的影响大,该实践结果检验了理论的正确性。
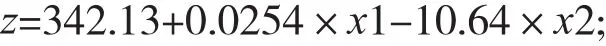
其中z:表示上导摆度,单位μm;
x1:表示净水头,单位m;
x2:表示出力,单位万kW。
3 结论与建议
对比2种数学模型估测数据,根据相对误差大小,发现线性拟合数学模型在计算水头和出力对振摆的影响程度方面更具有优势;多项式插值逼近数学模型输出的三维图谱观测效果更直观明了,且通过9组随机数据的相对误差结果验证了该种数学模型拟合原始散点数据建立三维图估测未知工况的方法是可靠有效的,该种依据现场实际数据进行数值模拟方式,为准确提供抽蓄电站稳定运行,负荷调节提供了一种新的手段。
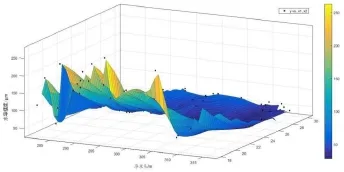
图6 水导多项式插值拟合结果
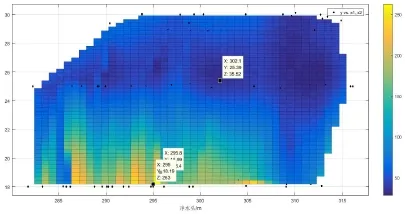
图7 水导多项式拟合数据估测
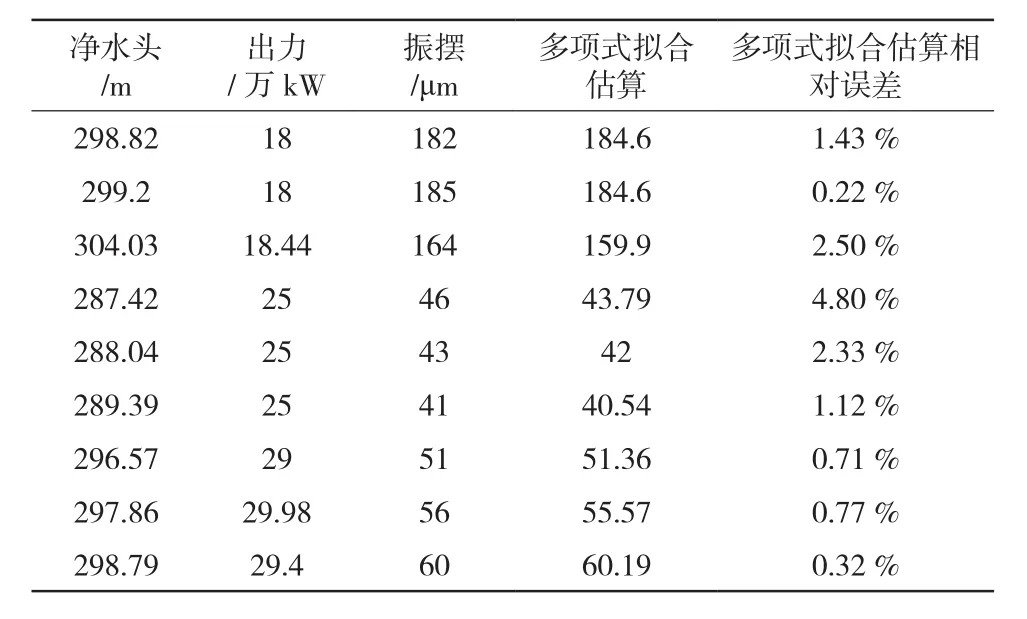
表3 水导摆度多项式拟合相对误差
根据研究中的突变点附近相对误差数值极大这一发现,将在后续的日常运维工作中,记录工况更详尽的散点数据修正模型,使得此三维数学模型预测结果更加精确可靠。
