基于数值模拟的T型管道流场参数正交优化

王 倩

(大庆油田有限责任公司测试技术服务分公司 黑龙江 大庆 163000)

0 引 言

T型管道具有结构简单、拆装方便等优点，在油、液、气输送中被广泛使用[1-2]。在这些领域应用的过程中对管道机械性能和流动性能都提出了新的要求。管道设计时，综合考虑管道这两种性能变得尤为重要，值深度研究。

目前，针对管道流场中流体的流动性等问题，有许多学者研究。魏显达等[3]通过Fluent软件有限元模拟三通内流体的速度、压力和温度场，获得了其对应的分布云图，为管材的选取和结构优化设计提供了指导。成蕾等[4]通过有限元模拟对支管口直径和流速对管内流体速度的影响规律进行探究，获得了避免出现涡流现象的流速上限和管径比。柳波等[5]利用双欧拉模型和Fluent对考虑温度场条件下喉管内气固两相流进行数值模拟仿真，获得了温度场对输送系统的两相流动特性的影响。韩思奇等[6]利用fluent对速度入口管径变化的流场进行了分析，获得了管径的变化与管道内流体的最高速度以及管道内涡旋直径的关系。邱立杰等[7]利用fluent对不同初始速度条件下弯管的内部流场进行了分析，获得了弯管压力场与速度场的变化及影响因素。纪宏超[8]等利用fluent数值模拟和有限元体积法研究了弯管油水两相流动的速度、压力、流线分步特性。白芳杰等[9]利用控制容积法,对热油管道停输后的自然对流进行了耦合求解,得到了管内典型流动洋相与等温线的变化,。梁之西[10]等利用fluent数值模拟管道内流体的偏流机制从而设计出使用的管道均流结构,可以有效的缓解由弯管管道存在而引起的一系列问题。虽然上述研究在管道流场中流体特性分析方面有所贡献，但主要集中在研究单个因素的影响，未能同时考虑多个因素的影响，并且未能对影响因素区分主次。

为此，本文以T型管为研究对象，提出正交优化理论与流场数值模拟相结合的方法来研究多个影响因素的作用以及各个影响因素的主次关系和各个参数的最优值。首先建立T型管模型，并通过流体方程对其进行分析，其次对其进行正交优化设计，最后对其进行数值模拟与正交试验设计与验证。

1 数值分析模型的建立

1.1 T型管模型的建立

采用NX10.0软件分别构建衔接处为直管的三维T型管模型。如图1所示为T型管几何示意图，其中d为管的内径，L1，L2分别为管段在出口段和入口段的长度。采用Fluent15.0对T型管内部流场进行有限元分析，有限元分析模型的几何参数如表1所示。

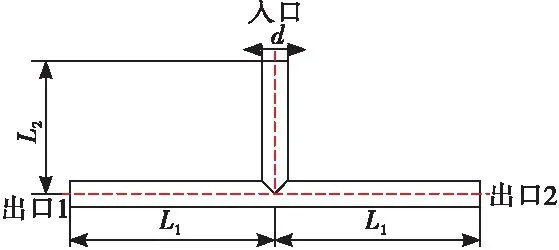
图1 T型管示意图

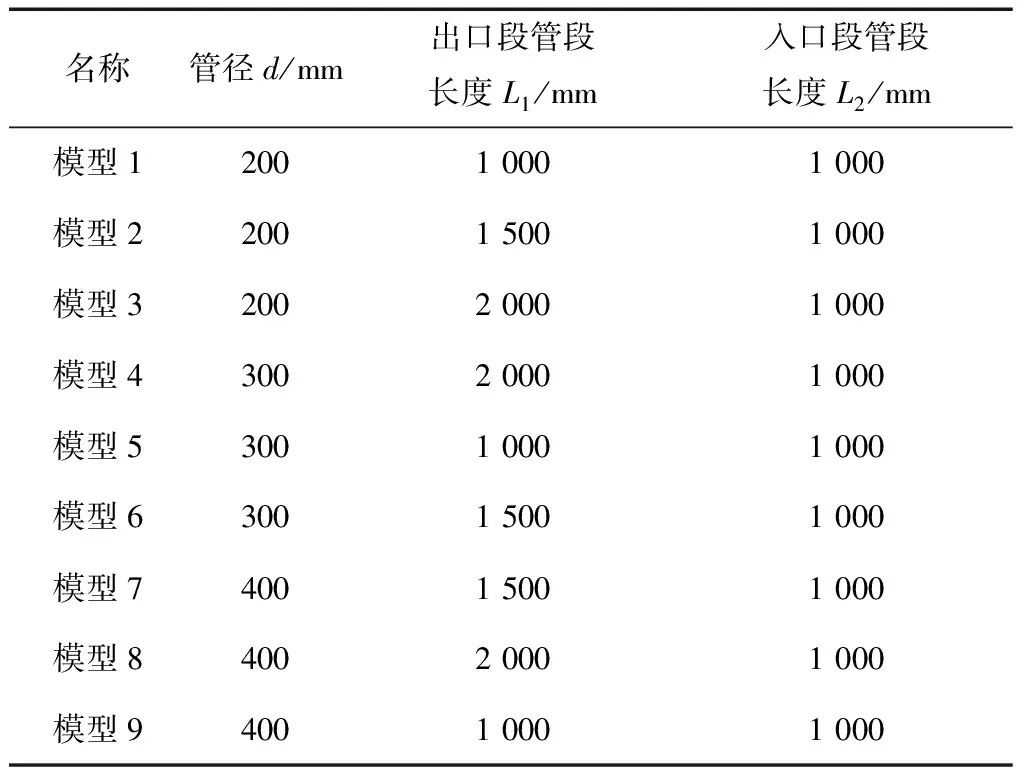
表1 T型管有限元模型几何参数

1.2 控制方程及边界条件

油气输送管道中，油气在三通管内的流动属于湍流，简化方程管道内的流体流动满足质量守恒、动量守恒、能量守恒、状态方程等。

1.2.1 连续方程

连续性方程(连续性方程式质量守恒定律在流体力学中的表现形式)在直角坐标系下表示为方程(1)。

跟踪相之间的界面是通过求解一相或者多相的容积比率的连续方程来完成的。对第q相，存在以下方程：

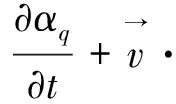
(1)

其中，αq为质量源项，在默认情形下方程(1)右端源项为0，但当给每一相指定常数或用户定义质量源，则右端不为0。主相体积分数的计算基于如下约束：

(2)

1.2.2 动量方程

通过求解整个区域内单一的动量方程，得到的速度场是由各相共享的。动量方程取决于通过属性ρ和μ的所有相的容积比率，方程如下：

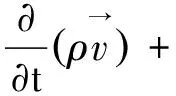
(3)

1.2.3 能量方程

能量方程在各相中也是共享的，表示如下：

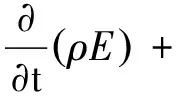
(4)

其中：keff为有效热导率；Sh为源项，包括辐射以及其他体积热源;E为总能量。

VOF模型处理能量E与温度T，作为质量平均变量:

(5)

这里每一相的Eq是基于该相的比热和共享温度得到。属性ρ和keff是被各相共享的。Sh包含辐射的贡献，也有其他的容积热源。

1.2.4 边界条件

假设混合流体的流动为稳态湍流流动，液相流体为不可压缩流且密度为常数，动力黏度为常数。为模拟实际状况，入口边界选择速度入口，给定入口速度的大小和方向，出口边界选为压力出口。

管壁为壁面边界，指定壁面为无滑移边界条件，壁面边界处采用标准壁面函数来处理。湍流模型采用标准k-ε模型。计算模型中考虑了重力，而对流动影响很小的升力、虚拟质量力等作用力进行了忽略。重力加速度为9.81 m/s2，方向为z轴方向。

2 不同参数的T型管道的正交优化设计

正交试验设计是利用正交表研究多因素多水平试验的优化方法，具有简单直观，便于多种方案寻优的优点。

本文将依据正交试验设计原理，设计T型管道正交优化设计因素水平表，在已确立正交试验因素水平表的基础上，结合实际要求来设计正交试验方案。

2.1 T型管道的试验因素及水平的确立

依据油气管道输送油气的物理和实际模型可知，管道的几何参数和油气物理性质对油气在管道中流动性具有较大影响。在此结合油气的主要物理性质和T型管的特点，选取管道内径、油气的流速、油温度和输送距离等影响油气流型的主要因素，建立T型管道的正交优化设计因素水平表，如表2所示。

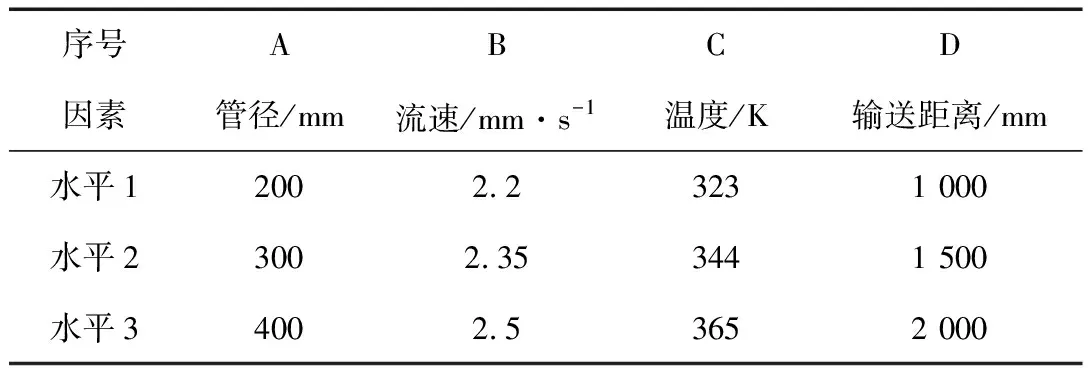
表2 T型管道正交优化设计因素水平表

2.2 T型管道优化设计正交表

结合已经确立的T型管道正交试验因素及水平，在不考虑各个试验因素交互作用的情况下，选取L9(34)正交表作为多指标正交优化试验方案，具体试验参数设置见表3。

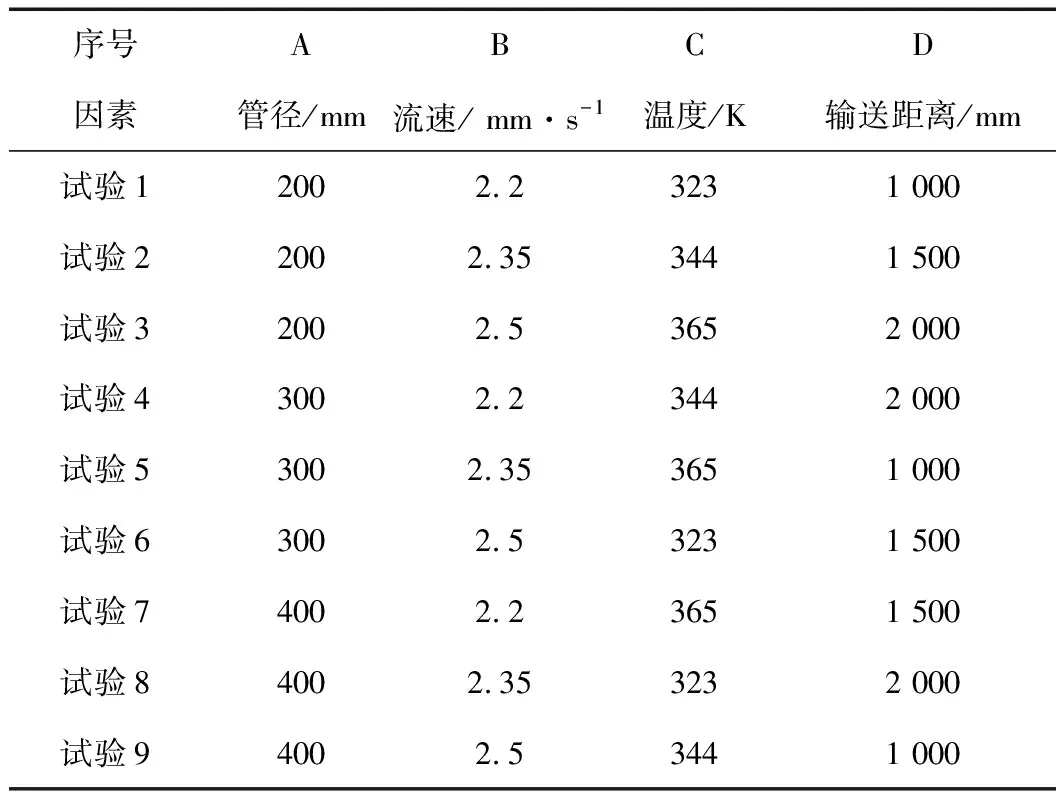
表3 正交试验方案

3 管道的油气流动数值模拟设置

目前对流体两相管流的研究方法主要有3种，即理论分析、试验测试、数值分析。由于数值分析相比前2种方法来说，具有理论要求和现场环境要求低的特点，所以在此选择数值模拟的方法。

本文利用NX10.0软件创建三维模型，并用ansys15.0自带mesh平台对模型计算域进行网格划分。

在建模软件中完成建模和网格划分，将模型导入软件。软件中包含求解器和后处理器，通过求解设置模拟实际情况，通过后处理得到油气混合流体管流的各流场分布，速度场、温度场等结果，通过图形工具直观地观察CFD数值模拟结果。

边界条件及求解设置，利用软件进行流体仿真计算，初始条件就是油气在管道流动中设置的操作环境，设置重力加速度。边界条件的设置要符合1.2节中选择流体理论模型和控制方程，同时尽量模拟实际工况，依照实际工况设置各个边界条件和参数。

在本研究中假设流体具有不可压缩性，采用基于压力型的求解，使用的是压力修正算法。

4 正交仿真试验与结果分析

在T型管道的正交优化设计和管道的油气流动数值模拟设置确立的基础上，利用fluent软件进行仿真模拟，得到各种工况下的流场情况。利用正交仿真试验的结果综合分析各因素的影响，对其结果极差分析确定主次因素，以入口处的流速和流量变化来衡量整个流场的流动性，并获得每个因素的最优水平；在以出口流速差作为试验指标时，通过方差分析来分析得到的流速与温度、输送距离之间的影响作用，最终获得所期望的最佳优化参数。结合图1数值仿真可以分为出口1试验和出口2试验2组数据进行，由正交试验结果分析表6和表7可得到表8。

由表8可知，T型管无论是出口1还是出口2输送时,管道内径和油的进口速度是流速和流量变化的主要因素，管道长度和温度均为次要因素，考虑到流量特性和流速特性越好时，均值越大，所以最佳组合均为：A3B3D1C2，即管道内径为400 mm，油在出口1的速度为2.5 m/s,管道长度为1 000 mm，油的温度为344 K。

流速与温度、输送距离之间影响作用的方差分析:选取显著性水平为a=0.05，根据F比的大小可知，影响管道内油气流速的重要因素为管径、输送速度、输送距离、温度，该结果与极差分析结果相一致，见表9。

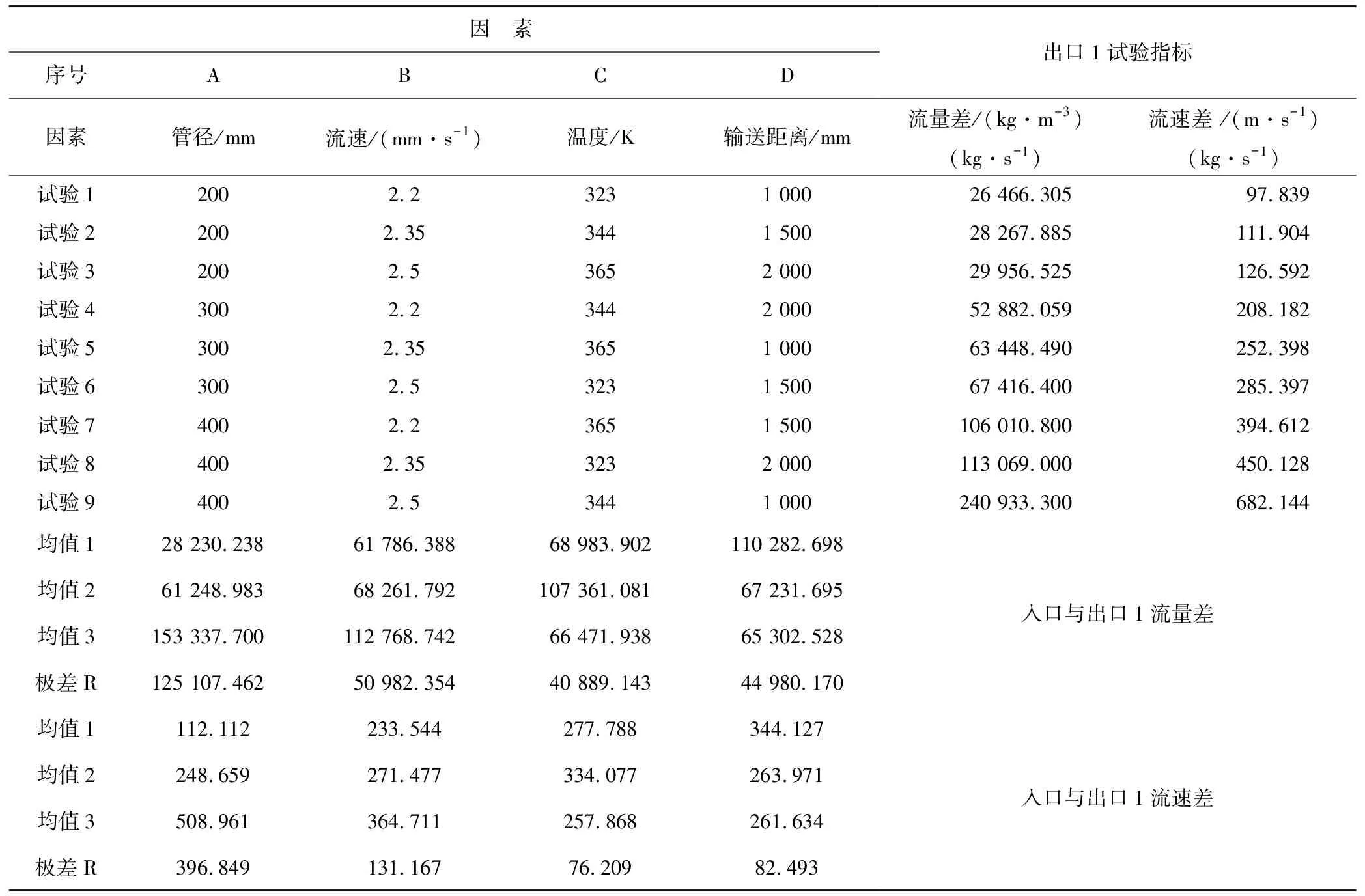
表6 出口1正交试验结果分析表

表7 出口2正交试验结果分析表

表8 正交试验结果极差分析表

表9 方差分析表

结合理论分析及正交试验的结果，得到如下结论：

1)在出口流量和流速变化这两项指标分析中，无论出口1和出口2，可以得出影响管道内油气流速的重要因素为管径(A)，输送速度(B)，输送距离(D)、温度(C)。那么这也说明油气在输送时，影响流量和流速变化的这4种因素的主次顺序是基本不变的。

2)综合考虑较优水平和影响重要性先后顺序，无论在出口1，还是出口2，考虑油气在管中的流动性，选取每种因素下的最大均值作为判定依据，获得均为A3B3D1C2，即管道内径为400 mm，油进口的速度为2.5 m/s，管道长度为1 000 mm，油的温度为344 K。

5 结束语

本文以工业常用的T型管道为研究对象，建立了数值分析模型，提出一种基于正交优化理论与数值模拟的T型管道流场参数优化方法。该方法通过对影响流动性的因素进行分析，获得了主要影响因素；采用了正交试验与Fluent软件有限元模拟相结合的方法进行了优化仿真试验，获得最佳流动性的管道几何参数和流体物理参数。利用该方法不仅可使得物理试验和模拟试验次数大大降低，便于加快产品的开发周期，同时为石油管道的参数和油气物理性质输送控制提供了理论依据和方法参照。