碳纤维复合材料的磨削热分配比仿真研究*

2019-03-08范宝朋陈斌斌梁宇红

金刚石与磨料磨具工程 2019年1期

范宝朋，陈燕，陈斌斌，梁宇红，孙亮

(南京航空航天大学，江苏省精密与微细制造技术重点实验室，南京 210016)

碳纤维增强树脂基复合材料(carbon fiber reinforced plastics，CFRP)具有轻质高强的特性，广泛应用于各个领域。在其应用过程中，为达到精度要求，需要进行精密加工[1-3]。磨削加工是一种常用的加工CFRP的方法[4-7]，但加工过程中磨削速度高、材料导热率低，会在磨削弧区产生高温，对加工表面产生不利的影响[5-8]，甚至会引起树脂基体降解[9]。另一方面，磨削液虽然有降温效果，但其中的油液、水分等会进入碳纤维复合材料中，造成碳纤维复合材料的膨胀与松弛，降低其模量与强度[10-11]，所以不能用于CFRP的磨削加工中。

为获得高质量的产品，应确保加工过程中产生的温度低于树脂基体材料的玻璃化转变温度。因此，磨削过程中的热量分配成为研究的热点。

在磨削加工中，磨削区内的磨粒与工件相互作用，所消耗的能量几乎全部转化为热量，并分配给工件、磨屑和磨具。对热量分配的相关研究在金属平面磨削中较多[12-13]，而对CFRP磨削过程中的热量分配研究却较少。经相关研究表明：磨削过程中热量传入工件的比例与磨削工艺有关[14]，且非金属与金属材料的热分配比存在差异[15]；由磨削过程中已知的工件表面温度反求传入工件的热量比例是一种可行的方法[16-17]，即通过试验方法得到总功率，计算出工件上消耗的功率，工件上消耗的功率与总功率之比即为传入工件的热分配比。但该方法计算量较大、计算较为烦琐，一般用有限元仿真技术来取代，文献[18]证明有限元仿真是一种有效的研究方法。

采用有限元仿真方法研究传入工件的热分配比，首先需要得到磨削过程中工件表面的温度。马海龙[19]使用K型热电偶埋在距工件表面1～2 mm处测量工件表面的磨削温度；YASHIRO等[20]铣削CFRP时将工件与刀具组成一组自然热电偶，将试验中获取的热电势值与标定好的电势-温度曲线相结合得到铣削过程中的温度值，实现了切边铣削中的温度精准测量。

CFRP磨削加工中，其温度的测量点距离磨削弧区有一定距离[19]，且磨削加工时砂轮与工件无法组成一组自然热电偶，不能准确测量磨削弧区的温度。在本研究中，用康铜丝与CFRP组成一组半人工热电偶，以其测量磨削弧区内的温度；通过调整仿真参数使工件表面温度与试验值一致，确定施加在工件表面的热流密度，从而得到消耗在工件上的功率，最终获得磨削过程中传入工件的热分配比。

1 工件表面磨削温度测量

磨削试验用机床及刀具如图1所示。机床型号为DMG HSC 20 linear超声辅助五轴精密加工中心，其最高转速42 000 r/min，功率5.5 kW，最大进给速度5 m/min，在X、Y、Z方向的最大行程分别为200、200、280 mm。磨削用钎焊金刚石刀具基体材料为304，钎料为Ag-Cu-Ti，钎焊金刚石磨粒粒径在140～150 μm之间，刀具直径6 mm，长度48 mm，螺旋角45°，齿数16。

磨削方式为干磨，工件材料为T700碳纤维增强复合材料(CFRP)，CFRP纤维方向角为90°，其纤维方向角φ定义为砂轮进给方向与纤维方向之间的夹角，如图2所示。试验材料及热电偶装夹方式如图3所示，工件材料及金刚石磨粒热特性参数如表1[15, 21]所示，磨削参数如表2所示。

(a) 机床Machine(b) 刀具Cutting tool图1 试验用机床及刀具Fig. 1 Machine and cutting tool used in the test

图2 纤维方向角Fig. 2 Fiber direction angle图3 工件装夹Fig. 3 Workpiece holding

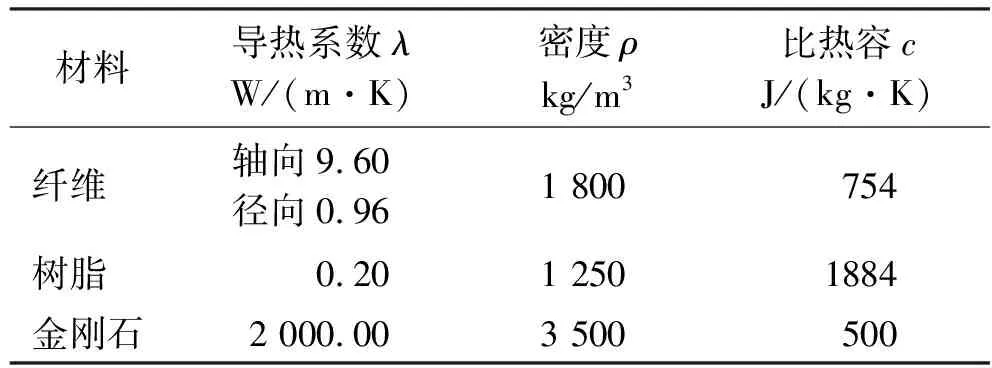
表1 工件材料及金刚石磨粒热特性参数

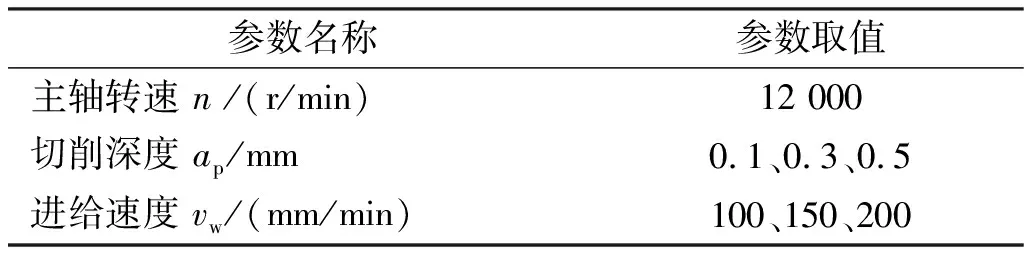
表2 试验磨削参数

1.1 磨削温度测量方法

使用半人工热电偶测量磨削过程中的温度，半人工热电偶组成方式如图4所示。半人工热电偶由CFRP板(13 mm×40 mm×2.5 mm)、康铜丝及云母片组成。康铜丝直径0.1 mm，压成薄片状；康铜丝与CFRP板间用厚度小于10 μm的云母片绝缘。由于材料自身的延展性，当康铜丝在磨削中被磨断时会与CFRP板搭接在一起，从而形成热接点，此热接点形成热电偶的热端，回路中便会产生热电势。实时记录热电势的大小就可间接获得磨削时磨削区域的温度。

在进行温度测量之前，需要对半人工热电偶进行标定。将标准K型热电偶与需标定的半人工热电偶在同一时刻置于同一温度中，使用NI USB 6211数据采集卡同时采集2种热电偶的电势。由于标准热电偶的电势与温度之间的关系已知，因此通过比较所标定的热电偶与标准热电偶相应的电势，便可以得到所标定热电偶电势与温度之间的关系。图5为热电偶标定曲线，图6为热电偶拟合曲线。

所标定的碳纤维复合材料-康铜丝半人工热电偶温度与电势曲线关系拟合结果为：

T=1.508+3.413e+3.023e2-0.218e3+6.955×10-3e4-83.629×10-6e5

(1)

其中：T为热接点温度，℃；e为相对应的热电势，mV。

1.2 磨削温度测量结果

在主轴转速为12 000 r/min，进给速度为100 mm/min，磨削深度为0.1 mm的条件下，通过磨削试验测得工件表面的温度，其结果如图7所示。从图7中可以看出：随磨削时间延长，磨削弧区逐渐接近康铜丝所在区域，测量的温度先缓慢升高后快速升高至最高点；当磨削弧区逐渐远离康铜丝所在区域时，半人工热电偶测得的温度逐渐降低。

在此磨削参数下模拟时，磨削弧区所有参与磨削的磨粒对温度贡献的统计平均值就是工件的表面温度[22]，其值为54.47 ℃。同样，在不同的主轴转速、进给速度及磨削深度下测量的磨削试验温度如表3所示。

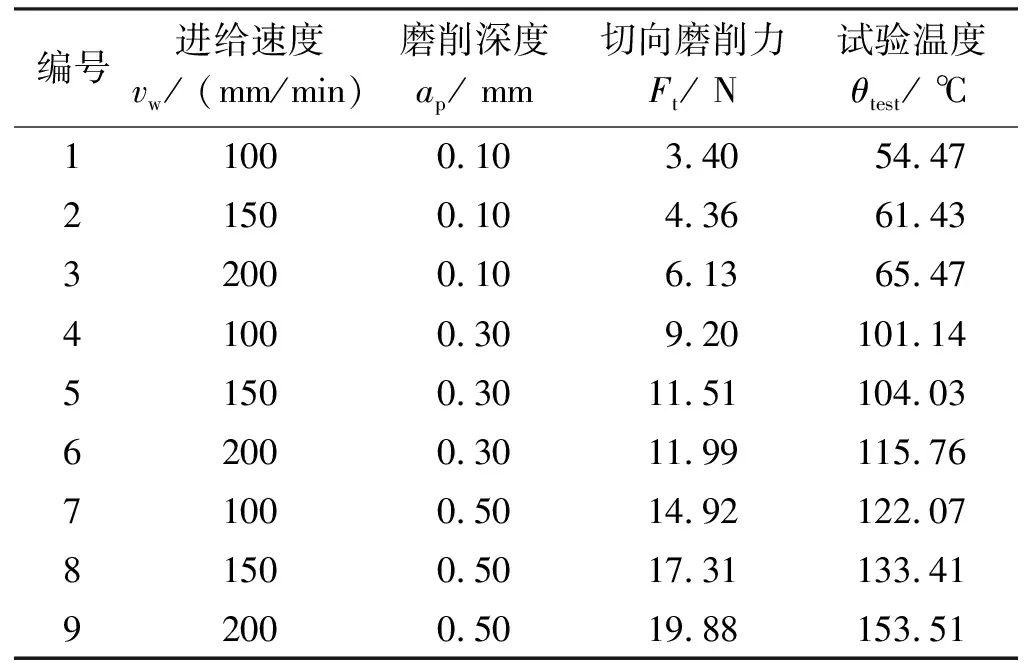
编号进给速度vw / (mm/min)磨削深度ap / mm切向磨削力Ft / N试验温度θtest / ℃11000.10 3.4054.4721500.10 4.3661.4332000.10 6.1365.4741000.30 9.20101.1451500.30 11.51104.0362000.30 11.99115.76 71000.50 14.92122.0781500.50 17.31133.4192000.50 19.88153.51

2 温度场的有限元仿真

2.1 热分配比计算公式

使用有限元仿真温度场的方法来计算传入工件的热分配比R。设磨削产生的总热流密度为Qt，传入CFRP工件的热流密度为Qw，则磨削CFRP时传入工件的热分配比R可下式计算:

R=Qw/Qt

(2)

总的热流密度Qt由公式(3)计算：

(3)

式中：b为刀具与工件接触宽度；lg为磨削区磨削弧长，Ft为切向磨削力，vs为刀具线速度。

磨削区接触弧长lg通过公式(4)计算：

(4)

式中：ap为磨削深度，de为刀具直径。

用磨削温度场仿真来计算热分配比时，先根据试验确定的切向磨削力计算出总热流密度Qt，再估算作用在工件表面的热流密度Qw，估算的方法是将仿真的温度与试验时所获得的温度值相对应，直至二者一致，从而得到各磨削参数下传入工件的热流密度，进而由式(2)得到传入工件的热分配比R。

2.2 温度场有限元仿真模型

利用Ansys软件对磨削时的温度进行仿真，可得到磨削弧区的温度值、各个位置的温度梯度及温度影响区域。磨削温度场有限元分析采用有8个单元节点数的三维热实体单元Solid70[18]，来实现瞬态温度场的仿真。碳纤维与树脂的材料参数见表1。

为了较准确地反映磨削温度在工件中的分布及影响区域，采用纤维与树脂材料分开的方法建立工件的两相模型。建立的模型基于以下假设：纤维与树脂紧密接触，忽略接触阻抗，纤维是正交各向异性均匀排列，树脂是各向同性均匀分布。

考虑到CFRP单根纤维直径只有7 μm，为避免划分的网格数量较多而无法计算，模型中工件厚度为一根纤维及包裹在其外围树脂的长度，即8 μm；根据前期的试验研究，模型大小设定为长4 mm、宽3 mm。

工件建模流程如图8所示：先建立碳纤维与其周围树脂的面模型(图8a)，并使用面映射网格对其进行网格划分(图8b)；然后，使用vext命令对划分过网格的工件表面进行拉伸，得到靠近工件表面的密集体网格和远离工件表面的稀疏体网格(图8c)，这样处理可在保证计算结果的精确性的同时缩短计算时间；最终完成的模型如图8d所示。图9、图10分别为树脂、纤维局部放大图。

模型热载荷以三角形热源的形式将热流密度施加在磨削弧区，热源大小为Qw，忽略空气对流换热。采用多次建立局部坐标系的方法模拟磨削过程中热源在工件表面的移动。

2.3 热分配比仿真结果

(a)碳纤维与树脂面模型Model of carbon fiber and resin surface (b)网格划分Mesh division(c)拉伸成体Stretched to form a body(d)工件模型Model of the workpiece图8 工件建模与网格划分Fig. 8 Workpiece modelling and mesh dividing

图9 树脂局部放大图Fig. 9 Enlarged drawing of resin图10 纤维局部放大图Fig. 10 Enlarged drawing of fiber

在主轴转速12 000 r/min，进给速度100 mm/min，磨削深度为0.1 mm的试验条件下，预估传入工件的热流密度值，对磨削弧区稳定后的温度值进行仿真，使温度仿真值与此参数下表3的实测磨削温度值54.47 ℃相一致，得到如图11所示的磨削仿真温度场。

将图7与图11进行对比，得到磨削温度试验与仿真信号对比图12。从图12可以看出：温度的试验与仿真信号具有较高的一致性。说明预估的热流密度可作为施加在工件表面的热流密度，将其代入公式(2)，计算出传入工件的热分配比R为2.2%。

利用相同方法，仿真确定各个磨削参数下传入工件的热流密度，代入公式(4)得到传入工件的热分配比结果，如表4所示。

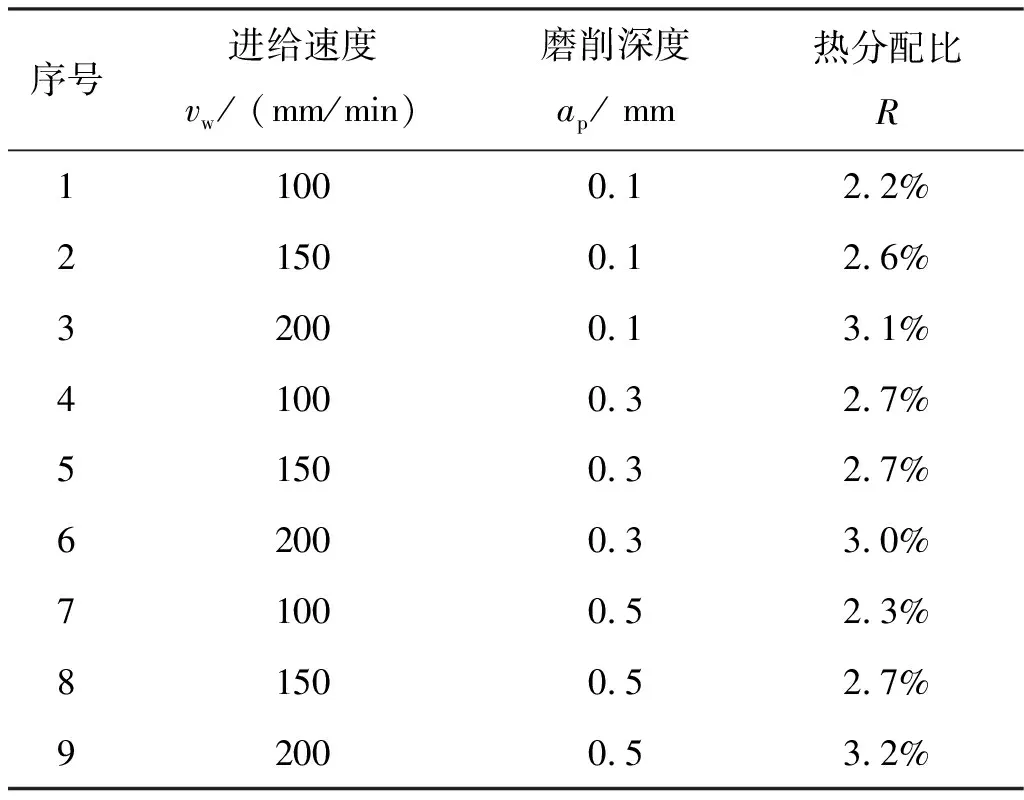
表4 热量分配比仿真结果

由表4可知：在此磨削参数下热分配比为2.2%～3.2%，说明磨削过程中产生的大部分热量都被磨削工具及切屑带走。出现此现象的原因之一是表1中金刚石磨粒的导热系数远大于碳纤维复合材料的导热系数，使大部分热量都传输给了金刚石磨粒。

将图11的磨削仿真温度场分开，分别得到如图13所示的树脂与纤维的温度场分布。由于表1中给出的纤维导热系数比树脂的导热系数大，导致磨削过程中所产生的热量沿纤维传导的深度大于树脂传导的深度，并且由于树脂较低的导热系数造成温度聚集，导致其最高温度要比纤维的大，图13a中的温度场深度与图13b中的温度场深度有差异就证明了这一点。另外，从图13还可以看到：温度场的形状是沿纤维方向延伸的，这也说明热量在树脂之间传导的难度要大于在纤维之间传导的难度。