自适应差分演化算法研究

摘要：差分演化算法的参数设置影响算法的优化性能和收敛速度。在对差分演化算法的控制参数：种群规模、缩放因子和交叉因子的取值进行详细实验基础上，分析各参数对算法性能的影响，总结参数选取规律，提出一种改进的自适应差分演化算法，该算法在迭代的每一代中，种群规模在一定范围内取值，缩放因子和交叉因子則在固定取值的基础上，按一定概率在一定范围内随机取值，使参数选择更宽松，增加算法的遍历性，避免陷入局部最优，提高算法收敛到全局最优的可能性。在基准函数的测试上，验证了新算法比传统差分演化算法具有更高的优化性能，并且简单容易实现。

关键词：差分演化算法;数值优化;参数分析;算法改进

中图分类号：TP301.6

文献标识码：A

文章编号：1009-3044（2019）36-0095一03

差分演化算法（Differential Evolution.DE）是Storn和Price于1995年提出的一种简单高效的随机启发式搜索算法[1]，该算法采用实数编码，具有原理简单、容易编程实现、参数少、收敛快速、鲁棒性强等优点，有很强的全局优化能力和很高的优化效率。但与其他进化算法一样，DE也具有容易陷入局部最优的缺点，并且算法性能对参数设置很敏感[2]。DE的可调参数虽然只有3个：种群规模NP，缩放因子F和交叉因子CR，但参数的设置对算法执行性能具有重大影响，选取不当会导致算法早熟停止进化。为了提高算法性能，研究者在参数控制与适应等方面提出了很多改进措施：文献[3]针对F和CR的综合作用进行测试分析并提出F=rand（.）的SDE版本;文献[4]提出了一种基于模糊控制的白适应FADE，利用模糊逻辑控制器对F和CR进行自适应控制;文献[5]提卅一种动态白适应群体规模的DE;文献[6]提出了一种自适应策略DE，算法中F采用随机正态分布产生，CR则通过演化过程中的反馈信息进行自适应调整;文献[7]对多种不同参数选取与控制策略进行比较分析，并证明了这些策略都在不同程度上提高了算法的收敛速度和优化精度;文献[8]对DE的3个参数展开实验研究，给出参数选取规则;文献[9]则提出了参数白适应学习策略。

本文在详细分析各参数对算法优化性能的影响规律基础上，提出种改进的自适应DE：算法在迭代的每一代中，NP在一定范围内取值，F和CR则在固定取值的基础上，按一定概率在某一范围内随机产生，通过随机参数来增加算法的多样性，避免陷入局部最优。

1差分演化算法原理

DE是一类基于群体的白适应全局优化算法，利用差分变异、交叉和选择等算子对群体不断进行演化，演化过程与遗传算法类似，也包括种群的表示与初始化、变异与交叉和选择操作。以经典DE策略之- DE/rand/bin为例对算法进行描述：

（1）种群表示与初始化：设求解问题的白变量有D维，种群规模为NP，则种群中第i个个体Xi表示为：xi={xi（1），xi（2），…，xi（D）}。初始化是在一定搜索空间内随机生成NP个D维向量构成初始种群。

（2）差分变异：对种群中的任意个体X.按式（1）生成一个对应的变异个体：

K=Xi1+F×（Xr2- Xr3）

（1）

式中：Xr1、Xr2和Xr3是当前群体随机选择的3个不同个体，而且它们也与Xi不同;Vi是变异个体;Xr2-Xr3为差分向量;F∈[O，1+]为缩放因子，用于对差分向量进行缩放，控制搜索步长。

（3）交叉：采用离散杂交操作，把目标个体X.和变异个体V.通过式（2）进行离散杂交得到测试个体Ui：

式中：Rj（0，1）是一个在（0，1）范围内的均匀随机数;Jran是[1，D]的一个随机整数，保证Ui中至少有一维来白Vi;CR∈[0，1]是交叉率，用来控制在哪些决策变量上采用变异值。

（4）选择：对每个测试个体Ui，采用式（3）的一对一竞标赛选择方式：

式中：F（Xi）为个体Xi的适应值;xi是代替Vi而进入下一代的子个体。

经过差分变异、交叉和选择操作，DE得到一个新的群体{xii=l，l，2，…，N}进入下一代，算法不断迭代直至满足终止条件退出。

2控制参数对算法性能的影响

DE算法控制参数有3个：群体规模NP，缩放因子F和交叉因子CR，这3个参数影响算法搜索精度和收敛速度。为了调查参数对算法性能的影响规律，本文使用4个典型的Benchmark函数作为实例（其中f1—f3是单峰函数，f4是多峰函数，所有函数全局最优值均为0），针对参数对算法性能的影响进行详细实验和分析：

2.1群体规模NP的影响

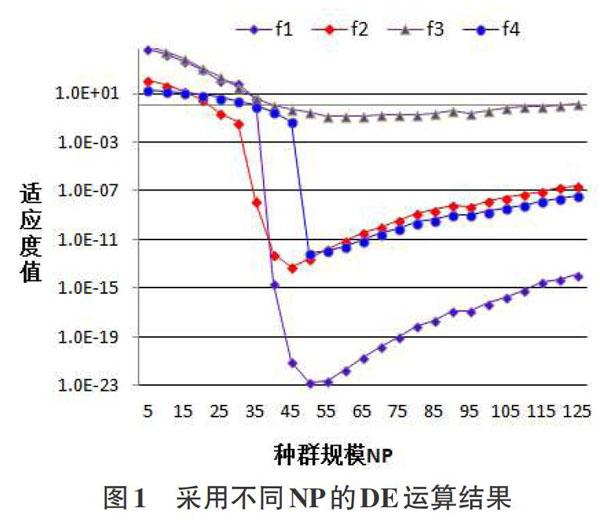
群体规模NP是群智能算法的一般性参数，其取值决定了算法的多样性，在一定程度上影响着算法的优化效率和优化质量。为了测试NP对算法性能的影响，在设定F=0.5和CR=0.9的情况下，把种群规模从5取到125，步长为5，采用上述函数对NP取值进行调查，函数维数D=30，迭代次数为1500。各个测试函数独立运行30次，取各次运行结果最优适应度值的平均值。测试结果如图1所示。

由图l可以看出：不论是单峰函数或多峰函数，在给定迭代次数（Gen=1500）的情况下，当NP在50附近时，算法取得的最优解精度最高，继续增大NP，算法的优化性能不仅没有改善反而出现下降。

这说明：种群规模太小，算法缺少多样性，收敛速度快但容易陷入局部最优;较大NP能够增加群体多样性，收敛到全局最优的可能性就越大，但所需的计算量也相应增加，降低收敛速度。在迭代次数不变情况下，有时种群规模的增大，反而会使最优解的精度降低。

因此，DE运行时必须考虑算法多样性和收敛速度的平衡，NP取值不能过大也不能过小。一般情况下，在给定最大迭代次数下，种群规模NP∈[30，60]时，算法能很好地保持种群多样性和收敛速度的平衡。

2.2缩放因子F和交叉因子CR的影响

缩放因子F用于控制差分向量对变异个体Vi（t）的影响，其取值在很大程度上同时影响着进化过程的收敛性及收敛速度。交叉因子CR控制个体的各维对交叉的参与程度，起到平衡全局与局部搜索能力的作用。

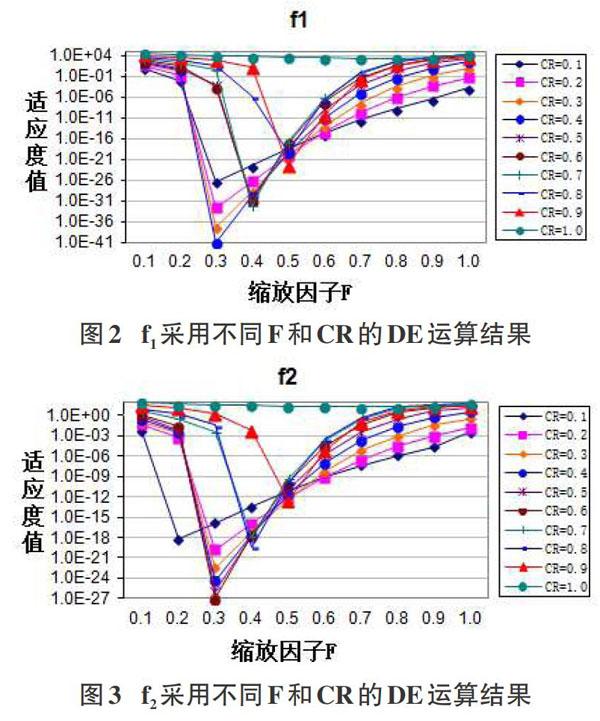
为了测试缩放因子和交叉因子对算法性能的影响，设定函數维数D=30，种群规模NP=50，迭代次数为1500，采用上述实例对F和CR取值进行调查。对每个实例，缩放因子F由0.1递增至1.0，步长为0.1;同时针对每个F值，交叉因子CR同样由0.1递增至1.0，步长也为0.1。各个函数运行30次，取各次运行结果的最优适应度值的平均值，比较各函数在不同F/CR取值组合的最优解变化情况，结果如图2～图5所示。

由图2～图5可以看出：

1）不论是单峰函数还是多峰函数，随着F增加，算法性能先变好后变差。当F在[0.3，0.6]取值时，算法能够取得较好的优化性能。

原因在于：F控制搜索步长，较小的F值产生的扰动较小，起到局部精细化搜索的作用，能够加速算法收敛，但容易使算法早熟收敛;较大的F值使差分向量（Xr2-Xr3）对变异个体Vi（t）的影响较大，产生较大扰动，增加算法跳出局部最优解的可能性，但当F>0.9时，算法近似随机搜索，降低收敛速度。因此，F取值不能过大也不能过小，一般建议设置在0.5左右。

2）单峰函数中，当CR ∈（0.5，0.9）时，算法优化性能较好;多峰函数中，当CR ∈（0.1，0.3）时，算法优化性能较好。特别地，当CR=0.9时算法取得的最优解精度较高。而当CR>0.9时，算法取得的最优解精度大幅下降。这就因为差分变异算子具有旋转不变性，即通过变异操作得到的变异向量Vi具有不随坐标轴旋转而改变的性质，这一特点使DE在CR=0.9时较适应求解变量相关的优化问题。

原因在于：CR本质上是用以调整历史信息和当前进化信息的权重，单峰函数中，较大的CR有利于保持种群多样性，搜索新的空间，加速收敛。而多峰函数中，CR的增加意味着对多变量相关的处理能力加强，也意味着Vi对子代的贡献增多。即个体间的非线性交互越少，越不容易形成自组织系统，因而对复杂问题的演化能力下降[10]。

3）图2～图5中，当F=0.5，CR=0.9时，算法都能取得较好的优化结果。因此，固定参数DE中，通常F取0.5，CR取0.9。3改进的自适应参数DE算法

通过算法参数测试得知，DE中的缩放因子F较好初始值为F=0.5，但当F∈（0.3，0.6）时算法的最优解仍能取得很高精度，甚至比F=0.5时更优;相对于F，交叉因子CR的取值比较自由，其较好的初始值是CR=0.9。但F和CR是相互影响的，对不同F（CR），最佳CR（F）取值不同。如果把F和CR设置为固定值或按某一规律变化，而不考虑具体优化模型和实现过程，容易使算法陷入局部最优。

为了提高DE的优化性能，减少人为设置参数对算法性能的影响，本文在固定参数DE的基础上，提出一种改进的自适应参数DE算法：该算法群体大小NP设置为[30，60]中的一个固定值，在迭代的每一代中，缩放因子和交叉因子在固定取值的基础上，按一定概率在一定范围内随机选取，通过让缩放因子和交叉因子在更大范围内的取值，提高算法的遍历性，提高算法收敛到全局最优的可能性。每个个体的控制参数取值策略如下：

其中，rn，dreal[a，6]是在[a，h]区间产生的均匀随机小数，y1和y2调节参数固定取值或随机取值的概率，即个体的控制参数部分取固定值，部分在一定范围内随机选取，让种群可以在更大范围内进行搜索，提高了算法的全局优化能力，并且避免了设置参数时的反复测试以及因参数设置不当而产生的误差。

将本文提出的自适应DE与固定参数DE（F=0.5、C R=0.9）的运算性能进行比较：空间维数D取30，NP=50，y1和y2取0.5，算法最大迭代次数为1500。各个函数随机运行30次，取各次运行结果的平均值。两种算法运算结果如表1所示。

由表1可以看出：

本文提出新算法除了在个别函数（f3）中优化效率没有明显提高之外，在大部分函数（f1、f2和f4）中都取得了比固定参数DE更好的结果，各个函数取得的平均适应度值和平均方差均低于固定参数DE所取得的结果，表明本文提出的新算法具有较高的优化精度，并且稳定性强。

自适应DE提高获得全局最优的可能性的原因在于：

1）固定参数DE把进化过程看成一个均匀向上的过程，但对于复杂、非线性、多峰值的函数，个体的进化是非线性的，收敛速度可能先快后慢，也可能先慢后快。

2） DE本质上是一种全局随机优化技术，对于不同优化问题，最佳的F和CR并非某一确定组合，而是在一定区域内波动。F和CR可以多种取值组合，传统的固定参数（F=0.5，CR=0.9）只是其中一个样本。白适应参数DE让个体在一个更宽松的环境迭代，增加找到全局最优的可能性。

3）由于算法中的选择操作采用了贪婪机制，优胜劣汰，阻止了比当前种群中最差解还差的解进入下一代，在进化后期种群将集中在一些极小值附近。自适应参数DE增加个体跳出局部极值的可能性，能够使种群从当前极小值的区域跳跃到另一个比当前区域更好的极小值区域，最终收敛到全局最优。

4结束语

差分演化算法控制参数的设置对算法搜索性能和收敛速度影响很大，不合理的参数设置可能导致算法早熟收敛或算法停滞。传统DE对缩放因子F和杂交概率CR设置很敏感，对不同的优化问题经常需要从问题本身出发设置、测试和调整参数，手动参数调整费时费力且效率低下。如何设置参数使算法既能避免早熟又能快速收敛，并且保持算法简单通用的优点，一直是DE研究的核心问题。

本文在分析控制参数对算法性能影响的基础上，提出一种白适应参数选择的DE，群体规模NP在一定范围内取固定值，个体控制参数在固定取值的基础上，让部分缩放因子F和杂交概率CR在一定范围内随机取值，通过增加参数的选取组合来提高算法收敛到全局最优的可能性。本文提出的新算法仅在参数选择上做出改进，没有复杂的调整策略和混合技术，算法流程与标准DE 一致，无须额外增加运算开销和数据存储空间，保持了DE算法实现简单、通用性强的优点，有利于算法进一步的推广和应用。

参考文献：

[1]Storn R，Price K.Differential evolution -A Simple and effi-cient adaptive scheme for global optimization over ContinuousSpace[R]. University of California， Berkley： ICSI， 1995.

[2] Storn R，Price K.Differential Evolution -A Simple and Effi-cient Heuristic for Global Optimization over Continuous Spaces[J]. Joumal of Global Optimization （S0925-5001）， 1997， 11（4）：341-359.

[3]谢晓锋，张文俊，张国瑞，等.差异演化的实验研究[J].控制与决策，2004， 19（1）：49-52.

[4] LIU J，LAMPINEN J.A Fuzzy Adaptive Differential EvolutionAlgorithm[Jl. Soft Computing， 2005， 9（6）：448-462.

[5] TEO J. Exploring Dynamic Self-adaptive Populations in Differ-ential Evolution[J]. Soft Computing， 2006， 10（8）：673-686.

[6] QIN A K，HUANG V L，SUGANTHAN P N.Differential Evo-lution Algorithm with Strategy Adaptation for Glohal Numeri-cal Optimization[J]. IEEE Transactions on Evolutionary Com-putation， 2009， 13（2）：398-417.

[7]高岳林，劉军民.差分进化算法的参数研究[J].黑龙江大学自然科学学报，2009， 26（1）：81-85.

[8]杨振宇，唐珂.差分进化算法参数控制与适应策略综述[J].智能系统学报，2011， 6（5）：415-423.

[9] ZHAN Z H，ZHANG J.Self-adaptive Differential EvolutionBased on PSO Learning Strategy[C]// In Proc. Genetic Evol.Comput. Conf.， 2010： 39-46.

[10]袁俊刚，孙治国，曲文吉.差异演化算法的数值模拟研究[J].系统仿真学报，2007， 19（20）：4646-4648.

【通联编辑：谢媛媛】

收稿日期：2019-10-29

作者简介：黄少荣（197 6-），女，教授，硕士，研究方向为计算机应用与计算智能。