八聚乙烯基POSS改性分散染料在p-POD纤维上吸附热力学与动力学研究

2019-03-07冒亚红

纺织科学与工程学报 2019年1期

冒亚红，管宇

(1.四川省纺织品生态染整高校重点实验室，四川成都611731;2.成都纺织高等专科学校，四川成都611731;3.中央军委后勤保障部军需军事代表局驻成都军事代表室，四川成都610015)

0 引言

聚对亚苯基1,3,4-噁二唑(p-POD)纤维具有十分优异的化学和热稳定性，尤其是极好的绝缘性能，但是该纤维耐光老化性能却比较差，尤其对紫外光更加敏感。同时，该纤维的染色也比较困难，染色纤维的色牢度比较低，限制了其在军事伪装等特殊领域的应用[1-4]。

本课题组制备了一种含有笼型低聚倍半硅氧烷(POSS)的改性分散染料，用于p-POD纤维高温高压染色，染色后纤维的抗紫外性能大幅提高，表观色深和色牢度都比较令人满意。同时，研究结果还表明改性染料以半嵌入的形式固着在纤维表层，对紫外光能够进行有效的选择性吸收。经紫外光照射后，染色纤维的表面形态、超分子结构、大分子聚合度、热稳定性等的保持都明显好于未染色纤维[5-6]。

为了进一步掌握改性分散染料在p-POD纤维上的吸附和扩散性能，更加合理的制定染色条件，本章着重讨论改性染料分子在p-POD纤维上的吸附机理，利用热力学和动力学手段深入分析染料分子的上染过程，未优化染色工艺提供理论依据。

1 理论部分

1.1 热力学基础

染料吸附等温线是指在一定温度下，达到染色平衡后，纤维上的染料浓度和染液中染料浓度的分配关系曲线，是设计吸附体系及染色工艺的重要依据[7]。一般认为分散染料上染合成纤维是按照溶解机理进行。纤维中的染料被视为固体溶质，在纤维中形成固溶体。染料从染液中上染纤维的过程，相当于染料在水溶液和纤维(无定形区)这两种互不相溶的溶剂间的分配，直至饱和，服从Nernst型分配关系[8]。

[D]f=K[D]s

(1)

式(1)中：[D]f为达到吸附平衡时纤维上的染料浓度；[D]s为达到吸附平衡时染液中的染料浓度。[D]f与[D]s成线性关系，斜率K为分配系数，它表示染料上染纤维的倾向大小[9]。

1.2 染色亲和力、染色热和染色熵

染色亲和力表示染料从染液中上染到纤维上的能力，是一个热力学参数。标准染色亲和力-Δμ°(kJ·mol-1)等于纤维上染料标准化学位-μf°和染液中染料标准化学位-μs°之差的负值[9]：

-Δμ°=-(μf°-μs°)

(2)

在一定温度下达到染色吸附平衡后，标准染色亲和力与纤维上染料活度af和染液中染料活度as有下列关系：

(3)

由于测定纤维和染液中活度较难，一般用染料浓度来代替活度，并假设活度系数等于1，因此有下列关系[10]：

(4)

式(4)中：R(8.314 J·mol-1·K-1)为气体常数；T(K)为绝对温标；[D]f(mg·g-1)表示纤维上染料浓度；[D]s(mg·L-1)表示溶液中染料浓度

V为每千克干纤维内相的上染有效容积，单位为L·kg-1。测定有效容积很难，特别是对涤纶这种疏水性纤维。因此，常常假设V=1 L·kg-1，故所测得的亲和力实际上是相对亲和力，但不影响比较分散染料上染指定纤维的亲和力大小。本实验中p-POD纤维的有效体积由氮气吸附-解吸附的方法测得，Vp-POD=0.78 L·kg-1，见3.2节[11]。

染色过程中纤维从染液中吸附染料，伴随着体系分子间作用力的拆散和重建，发生吸热和放热反应。标准染色热是无限小量的染料在标准状态下，从染液中向纤维转移时，每摩尔染料转移所吸收的热量。染色热的大小可反映染料和纤维分子间结合力的强弱和结合方式，结合力越强，放热越多，不仅染料上染纤维的倾向大，而且被纤维吸附后也不易解吸下来。由Gibbs-Helmholts方程(式5)求出ΔH°[11]。

(5)

式(5)中：ΔH°(kJ·mol-1)表示吸附热；-Δμ1°和-Δμ2°分别表示不同温度下的标准亲和力。

染料从染液中被吸附到纤维上，会带来体系微观状态函数的变化。染色熵是表示染色体系混乱度的一个状态函数，它与染料在纤维上的结合状态、配向程度和染色牢度有关。标准染色熵就是无限小量的染料在标准状态下从染液中向纤维转移时，每摩尔染料转移引起的染色体系熵的变化。大多数场合下，染色熵为负值，即染料从溶液中上染到纤维，体系的混乱度是降低的。一定温度下，染色熵可按式(6)由标准染色亲和力及染色热近似计算[12]：

-Δμ°=TΔS°-ΔH°

(6)

式(6)中：ΔS°(J·mol-1·K-1)表示不同温度下熵的变化。从式(6)可以看出，染料对纤维的亲和力取决于染色热和染色熵。低温下染色热起主要作用，绝对零度时亲和力完全由ΔH°值决定。随着温度的升高，染色熵的贡献增大，在高温下ΔS°对纤维亲和力影响变得愈为重要，在染料实际上染纤维的过程中，两项都起着重要的作用。

1.3 扩散系数和扩散活化能

在染色过程中，染料逐渐从染液中向纤维上转移，随着时间的推移，纤维上的染料逐渐增加，而染液中的染料逐渐减少。以上染百分率为纵坐标，染色时间为横坐标绘制得到的上染速率曲线，是研究染色动力学的基础。

本实验采用的染液浴比较大，且搅拌充分，可以近似假定该染色过程为无限染浴上染过程。因此，根据Wilson和Crank有关染色动力学理论的研究，表明无限长的圆柱形纤维在有限染浴中的上染速率与下列参数有关[13]：

(7)

式(7)中：Mt(mg·g-1)为在t时刻纤维上的染料浓度，M(mg·g-1)为吸附平衡时纤维上的染料浓度；Df(m2·min-1)为染料在纤维中的扩散系数(通常假定它不随纤维上染料浓度而变化)；t(min)为染色时间；r(μm)为纤维半径；E为染色平衡时染料的上染百分率；L为与扩散边界层厚度有关的无量纲参数。L与下列参数有关[14]：

(8)

式(8)中：Db为染料在染液中的扩散系数；K为染料在纤维和染液间的分配系数；δD为扩散边界层的厚度，它很大程度上取决于染液的流速，流速越快，厚度越薄。

如果染色时间不长，式(7)可用Hill公式(9)代替[15]：

(9)

从式(4.10)中可以看出，染料的上染速率Mt/M主要与三个变量有关，即Df·t/r2，L和E。E取决于染料的亲和力，也和纤维的无定形区含量有关；Df·t/r2不仅和染料的性质及纤维的微结构有关，在很大程度上还随纤维的半径变化而变化；L不仅和染料性质、纤维微结构及半径有关，还和染液流动状态有密切关系，因为扩散边界层厚度随染液流速变化而变化。因此，在染色条件(例如染液温度、浴比、染液流动状态等)一定的情况下，上染速率主要取决于染料的性质(亲和力和扩散性能)和纤维的结构(分子结构、超分子结构、截面形状、线密度和表面结构特征)[9]。

扩散系数是反映染料在纤维中扩散性能的一个参数，它是由染料和纤维的化学结构和纤维微结构决定，并随着温度、助剂、染液pH值等外界条件而变化。半染时间是上染达到平衡吸附量一半所需的时间，以t1/2表示，它是表示上染过程趋向平衡的一个常用速率指标。

在无限染浴中上染时，实际上Mt和M是指单位重量纤维上的染料量，所以Mt/M等于ct/c；Mt/M仅随Df·t1/2/r2变化，因此在上染量达到平衡吸附量一半，即Mt/M=0.5时，此时t=t1/2，Df·t1/2/r2对应有一定值[16]：

(10)

本实验中和p-POD纤维的半径r(μm)由电子显微镜(Hitachi,Ltd,Tokyo,Japan)测得，它们的平均半径10.95 μm。染色浴比为2000:1，符合无限染浴的要求，并假定和p-POD纤维的结构均匀，均为圆柱体，如果半染时间t1/2己知，就可以根据式(10)计算出扩散系数Df。

扩散活化能是指分散染料在纤维中扩散克服阻力所需要的能量。在不同染色温度下，可根据Arrhenius方程计算出分散染料在不同纤维中的扩散活化能[17]。

(11)

式(11)中：T1和T2分别代表绝对温度；E(kJ·mol-1)为分散染料的扩散活化能，R(8.314 J·mol-1·K-1)为气体常数；D1和D2(m2·min-1)分别代表不同温度条件下所对应的扩散系数。

1.4 吸附动力学方程

为了进一步了解POSS改性分散染料在p-POD处理纤维上的吸附历程，掌握其染色的本质过程，更好地运用动力学理论优化染色条件，故引入化学动力学方程对该吸附扩散过程加以讨论。

假一级动力学方程也被称为Langergren方程[18,19]，见下式：

(12)

式(12)中：k1(min-1)表示假一级吸附速率常数。再对式(12)进行积分并带入边界条件，得式(13)和(14)：

log(C-Ct)=logC

(13)

hi,1=k1C

(14)

式(14)中：hi,1(mg·g-1·min-1)表示假一级模型的初染速率。

假二级动力学模型是基于平衡吸附量推导得出的[18,19]，见式(15)：

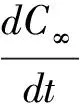
(15)

式(15)中：k2(g·mg-1·min-1)表示假二级吸附速率常数。再对式(15)进行积分并带入边界条件，得式(16)和(17)：

(16)

(17)

式(17)中：hi,2(mg·g-1·min-1)表示假二级模型的初染速率。

2 实验部分

2.1 主要原料

聚对亚苯基-1,3,4-噁二唑纤维(p-POD)由实验室自行制备[20-21]，为了去除纤维表面在纺丝过程中残留的油剂和其他化学药品，纤维使用前分别在丙酮和乙醇中浸泡20 min，然后再经过冷水洗、热水洗、冷水洗，并在室温通风环境下自然晾干。

POSS改性分散红60(见结构式4.1)由上海Dyestar公司提供，具体合成方法见参考文献6[6]。丙酮、冰醋酸和N,N-二甲基甲酰胺均为分析纯，由成都科龙化工厂提供。

结构式4.1 POSS改性分散红60

2.2 孔隙率的测量

采用氮气吸附-解吸附的方法测试纤维表面的吸附和孔隙特性。所有待测样品均需在真空仪中放置24小时，以去除纤维中原来含有的气体[22]。然后在Micromeritics Tristar 3000表面积和微孔测试仪中(US Micromeritics Ltd.)进行测试，由设备自带软件按照BET法计算得到纤维的孔隙率[23,24]。

2.3 染液的吸光度-浓度标准工作曲线的绘制

采用Shimadzu UV-2401PC型紫外-可见光分光光度计在染液的最大吸收波长处 (λmax=520nm) 测定染液浓度。测试溶液由水和N,N-二甲基甲酰胺按体积比1:1的比例配制而成，再用稀释的冰醋酸溶液调整pH值为5.0 ± 0.2[11]。染液吸光度-浓度的标准工作曲线见图1。

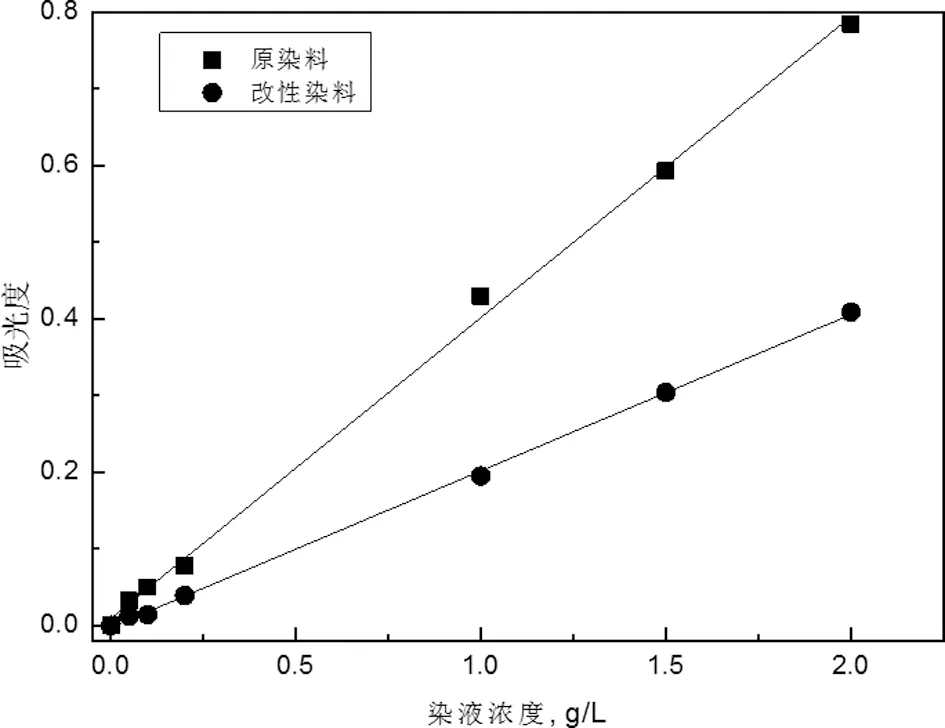
图1 POSS改性分散红60 H2O/DMF溶液浓度-吸光度标准工作曲线

2.4 吸附等温线的绘制

用去离子水配制各种浓度(0.05-1.0 g·L-1)的染液，用冰醋酸溶液调整pH值为5.0 ± 0.2。为了便于比较，将纯染料和改性染料溶液分别放入装有0.1gp-POD纤维的锥形瓶中，然后装上球形冷凝管，在规定的温度下回流冷凝染色96小时。染液的浴比为2000:1，其目的是为了把染液看作无限染浴。实验结束后，从染色残液中抽取1 ml残液与N,N-二甲基甲酰胺配成体积比1:1的溶液，以测定其染料浓度[25]。

2.5 上染速率曲线的绘制

将0.1 g干纤维放入装有200 mL染液(20 mg·L-1)的锥形瓶中，装上回流冷凝管，分别在50℃和90℃下回流保温。实验开始后，每隔几分钟就从染液中取出0.2 mL溶液，测定染液浓度，并计算得到纤维上染料浓度[25]。

3 结果与讨论

3.1 吸附等温线

图2(a)和(b)分别为50℃、70℃和90℃条件下，原染料和POSS改性染料在p-POD纤维上的吸附等温线。图中数据显示，所有试样纤维上染料小于吸附饱吸附量时，染料在纤维上的平衡吸附量([D]f)均随着染液浓度([D]s)的提高而呈线性上升，也就是说，[D]f与[D]s间呈线性关系，这六条吸附等温线满足Nernst型吸附模型(见式18)。因此，这两种染料在p-POD纤维上的吸附可以被看作固体染料在两种互不相溶的溶剂(水和纤维)中转移和分配，并且与纤维形成固溶体，其吸附等温线的热力学参数见表1。

[D]f=[D]N=KN[D]s

(18)

式中：[D]N(mg·g-1)为以Nernst吸附模型计算得到的理论吸附量；KN(L·g-1)为Nernst型吸附的分配系数。

(a)原染料

图2 原染料和POSS改性染料在p-POD纤维上的吸附等温线

表1 原染料和POSS改性染料在p-POD纤维上的吸附等温线参数

注：[S]O和 [S]1分别为原染料和改性染料在p-POD纤维上的饱和吸附量；KN为Nernst模型分配系数；R2为相关系数。

通过比较这两组热力学参数，在相同的染色温度下，原染料在p-POD纤维上的饱和吸附量和对应的相关系数(R2)都要略大于POSS改性染料。这可能应为改性后染料体积略微增大，染料向纤维内部扩散所受空间阻碍增大，在相同浓度梯度的作用下，染料吸附和扩散的能力有所下降，也正因为染料向纤维内部扩散变得困难，改性染料在纤维表面发生单分子层吸附的趋势逐步增大，其参数与Nernst吸附模型的理论值的差距也逐步变大。

3.2 标准亲和力、染色热和染色熵

标准亲和力、染色热和染色熵常被用来描述染料对纤维或织物的染色能力。对于一个特定的染色过程，当染色温度、压力和和染液成分不变时，它们仅仅由染料和纤维的性质所决定[18]。上节已经证明，原染料和POSS改性染料在p-POD纤维上的吸附，可以用Nernst吸附等温式表示，其染色亲和力、染色热和染色熵可根据式(4)～(6)计算得到，见表2。

表2 原染料和改性染料在p-POD纤维上的染色亲和力、染色热和染色熵

样品-Δμ0 (kJ·mol-1)50℃90℃-ΔH0(kJ·mol-1)-ΔS0(J·mol-1·K-1)原染料14.4913.8619.5815.76改性染料13.8812.7323.1628.73

染色亲和力表示染料从标准溶液状态向标准纤维状态转移的趋势，数值越大，则表示在纤维上发生吸附的趋势越大[26]。表2数据显示，在50℃和90℃条件下，两种染料的染色亲和力均大于零，且原染料与p-POD纤维的亲和力要高于改性染料。这一方面说明采用POSS改性染料对p-POD纤维进行染色是切实可行的；另一方面也说明了由于采用POSS对染料进行接枝改性，在染料分子中引入POSS结构，改变了染料分子的极性和染料分子电子云的共面性，从而削弱了染料分子与芳香族p-POD大分子间的范德华力作用，减弱了染料分子从染液向纤维转移的趋势的。同时，还发现这两个染色过程中的染色热均小于零，且改性染料的绝对值更大。这说明两种染料在p-POD纤维上的吸附都是放热过程，升高温度对染料的吸附是不利的，并对于改性染料尤其不利，这一结论在染色标准亲和力随温度的升高而降低也得到了证明。

在热力学理论中，熵被用来表示体系的无序程度或混乱度[26-27]。表2数据显示，这两个染色过程的熵变值均为负数，而且改性染料的数值更小。在染色过程中，由于染料分子与纤维大分子间的相互作用，染料的热运动受到限制，体系的混乱程度下降，染色熵一般小于零。由于改性染料吸附在p-POD纤维上放出的热量和熵减量更大，说明仅从热力学角度讲，染色温度越低，对于染料上染越有利。但实际情况却完全相反。这种反常现象一方面是由于p-POD的玻璃化温度远高于目前实验温度，在此温度下，染料分子在p-POD中的扩散还比较困难；另一方面，由于范德华力在染料与p-POD纤维的吸附过程中起主要作用，染料的扩散受到p-POD大分子链上苯环和噁二唑环的束缚。因此，对于POSS改性染料在p-POD纤维上的吸附过程，动力学因素的影响远远大于热力学因素的影响。换句话说，POSS改性染料上染p-POD纤维，是一个动力学控制过程。

3.3 扩散系数和扩散活化能

图3是原染料和改性染料在p-POD纤维上的上染速率曲线。从图中曲线可以看出，较高的染色温度能够获得较高的初染速率。再通过比较各条曲线的斜率，发现原染料上染纤维受温度的影响最为明显，而改性染料体系的变化相对比较缓和。随着温度的提高，特别是升到90℃，其纤维大分子链的热运动和染料分子的扩散能力被大大增强，因此，吸附动力学曲线的斜率和饱和吸附量也明显增大。因此，这一实验现象也进一步证明了改性分散染料在p-POD纤维上的吸附是一个动力学控制过程。

图3 原染料和POSS改性染料在p-POD纤维的上染速率曲线

扩散系数和扩散活化能一般被用来表示染料分子在纤维内扩散能力，较高的扩散系数和较低的扩散活化能表示染料分子在纤维内的扩散阻力较小，易于扩散[13]。表3数据表明，每种染料扩散系数均随着温度的升高而增大，且原染料的上升趋势最明显，其具体原因与上染速率曲线性状变化的原因相一致，这里不再赘述。同时，在相同温度下，原染料在纤维中的扩散系数最大，而改性染料较小。这主要是因为改性染料的体积大于原染料，染料分子向纤维内部扩散过程中，受到的空间阻碍就较大。由于在较低温度时，p-POD纤维大分子热运动不显著，染料分子大小差异引起的扩散能力上的差异也不明显。温度升高后，p-POD大分子运动加剧，大分子链间的瞬时空隙和无定形区增大，而改性染料进入纤维仍旧困难，因此，由空间阻碍引起的扩散性能差异也就更加明显。

对于扩散活化能，改性染料的对应值小于原染料，这表明原染料扩散更加容易。这一点与实际染色过程是相违背的。由于改性染料分子体积较大，以前的研究表明，改性染料也仅仅能够以半嵌入的形式进入表面层，染料分子仍就不能进入纤维内芯[5]。因此，在计算p-POD的扩散系数时采用纤维半径(r)的数值实为实际半径的五分之二[5]。但从总体上讲，改性染料在整个p-POD纤维中的扩散趋势要弱于原染料。

表3 原染料和改性染料在p-POD纤维上的扩散系数和活化能

样品Df(×10-14 m2/min)50 ℃90 ℃E (kJ/mol)原染料1.4693.00617.482改性染料1.2061.4013.653

注：Df为扩散系数；E为扩散活化能。染色p-POD纤维的染透厚度为纤维半径的2/5，在计算p-POD纤维扩散系数时使用r= 2/5 ×10.95 μm[16]，其直接证据见图3。

3.4 吸附速率方程

为了进一步研究改性染料在p-POD纤维上的吸附动力学，采用假一级和假二级动力学方程来验证图3中的动力学数据。根据式(13)和(16)，分别以log(C∞-Ct)对时间和以t/Ct对时间作图，得到图4和5。利用两图中直线的斜率和截距可以分别计算得到最大吸附量(C∞)、假一级速率常数(k1)和假二级速率常数(k2)，以及两种动力学模型的初染速率(hi,1和hi,2)，见表4。

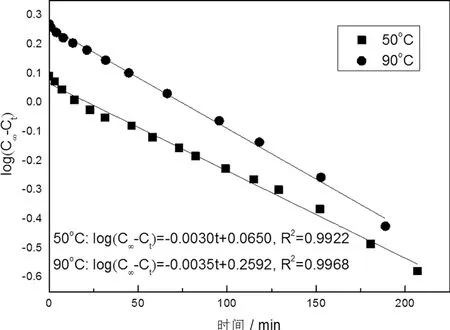
图4 改性染料在p-POD纤维上吸附的假一级动力学方程曲线

图5 改性染料在p-POD纤维上吸附的假二级动力学方程曲线

表4 改性染料在p-POD纤维上的吸附速率参数

注：k1(min-1)和k2(g/mg·min)分别是假一级和假二级吸附速率常数；hi,1和hi,2(mg/g·min)分别是假一级和假二级模型的初染速率；C∞(mg/g)为最大吸附量；R2为相关系数。

表4中数据显示，在每个温度下，假一级方程的相关系数(R2)都要高于假二级方程，这表明该吸附扩散过程更符合假一级动力学模型。再者，通过比较不同温度下的速率常数(k1)和初染速率(hi,1)发现，温度越高k1和hi,1越高，这说明较高的温度更加有利于改性染料在p-POD纤维上发生吸附。同时，结合热力学部分的结果，改性染料在纤维上的饱和吸附量(C∞)也随温度的上升而增加(C∞,50=1.230 mg/g,C∞,90=1.863 mg/g)，这充分证明了该染色过程是动力学控制过程。