矿山爆破振动载荷下框架结构的动力响应分析

米中阳，张智宇，黄永辉，雷 振

(1. 昆明理工大学 国土资源工程学院，昆明 650093；2. 昆明理工大学爆破新技术应用研究所，昆明 650093；3. 贵州理工学院 矿业工程学院，贵阳 550003)

随着社会的发展，爆破技术得到了广泛的应用，爆破诱发的一系列的负面效应尤其是爆破地震效应问题受到了人们普遍的关注和重视[1]。曹孝君等通过对各种爆破条件下的爆破地震波的特性分析和建筑物破坏现象、结构动力响应参数和结构动力特性参数的测试工作，对爆破振动在爆破地震波的特性、传播规律及爆破地震波与建筑物动力响应的关系等方面做了大量的研究，并且取得了一定的成果[2]。

爆破地震波对建筑物的影响本质上是结构的动力响应问题，建筑物在爆破地震波荷载作用下，由于基础运动而引起结构振动，爆破振动破坏效应不仅与地表振动强度参数有关，同时与爆破地震波频率及振动持续时间也有较大的相关性，爆破振动破坏效应是结构体动态破坏问题，其对结构体的破坏效应实际上是一个动力响应过程[3]。高富强[4]等基于结构动力学理论，利用ANASYS/LS-DYNA软件构建了数值模型，综合了地震波的振幅、频率及结构特征等对结构振动的影响，对结构在爆破振动作用下的响应过程进行了系统分析。黄志强[5]等通过采用结构动力学原理，对结构在爆破振动激励下的动力响应进行了计算分析，并运用ANSYS软件对烟囱结构在爆破振动下的响应情况进行了数值模拟，结果表明，随着烟囱高度的增加，其位移响应也越大。魏晓林[6]的研究表明，炸药量和爆心距是影响振动的主要因素，建筑物自身频率对爆破振动的放大程度起着决定性作用。

由于矿山爆破装药量大、爆破次数频繁，与其他爆破相比爆破的地震效应较强，对周围建筑的影响较大。随着某矿矿体开采逐步向矿办公区及住宅区和周边村庄推进，以及多次爆破振动会对建筑结构产生累积振损，该矿山爆破对周边建筑结构产生的危害越来越大，有必要对矿山爆破对邻近框架建筑结构的影响进行研究，从而为建筑物的现场监测提供一定依据。

本文采用动力有限元分析方法，对矿山爆破振动载荷下的建筑结构动力响应进行了研究，通过有限元软件ANSYS/LS-DYNA建立该矿办公楼五层混凝土框架结构有限元模型，将现场实测的爆破振动波形输入建筑基础，分析了建筑结构的动力响应情况，并参照相关标准[7]判断建筑结构的破坏程度。

1 办公楼数值模型构建

1.1 材料模型的选取及约束条件

对筋混凝土的密度取为2 500 kg/m3，梁、柱采用C30混凝土，弹性模量取值E=30 GPa，楼板采用C25混凝土，弹性模量取值E=28 GPa，混凝土材料泊松比取为0.2。对于钢筋混凝土结构，结构阻尼比ζ取0.05。计算中未考虑土与上部结构共同作用，基础与地基刚性连接，即约束与地面接触的框架柱以及剪力墙上节点的所有自由度。

1.2 三维有限元模型

建立办公楼有限元模型如图1所示。在该模型中，节点总数为22 330个，单元总数为26 838个。模型水平面中以模型的长边方向为x轴方向，短边方向为y轴方向，以竖直向上方向为z轴方向。此外，该计算分析模型未考虑填充墙的影响。

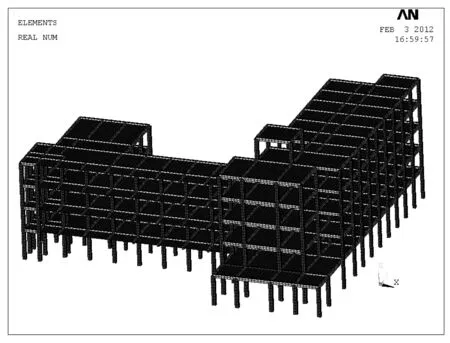
图1 某办公楼有限元模型Fig.1 Finite element model of phosphate office building

2 办公楼三维有限元动力分析

2.1 提取计算分析用爆破振动波

二采区2050-2040水平和三采区2110-2100水平爆破时，对矿办楼1楼、3楼和5楼进行了两次实测。对比二采区开采爆破时所监测的办公楼1楼振动波速曲线和三采区开采爆破时所监测的办公楼1楼振动波速曲线，发现二采区开采爆破时所监测的办公楼1楼振动波速相对较大。因此，选取如图2所示二采区开采爆破时所监测的办公楼1楼振动波速曲线作为该矿办公楼动力响应计算分析用爆破振动波。

图2 该矿办公楼动力响应分析用爆破振动速度波Fig.2 Blasting vibration velocity wave for dynamic response analysis of office building in this mine

该矿办公楼动力响应分析采用10 s时间历程爆破振动加速度时程曲线分别如图3至图5所示。

图3 水平径向加速度时程曲线Fig.3 Horizontal radial acceleration time-history curve

图4 水平切向加速度时程曲线Fig.4 Horizontal tangential acceleration time-history curve

图5 垂直方向加速度时程曲线Fig.5 Vertical acceleration time-history curve

将实际的爆破振动波输入爆破振动波加速度时程曲线，并利用公式(1)和公式(2)将加速度时程转换为应力时程。

σs=-2(ρCs)νs

(1)

σn=-2(ρCp)νn

(2)

式中，σs、σn分别为施加在静态边界上的法向应力和切向应力，ρ为介质密度，Cp和Cs分别为介质P波和S波的波速，νn和νs分别为结构模型边界上法向和切向的速度分量。

2.2 办公楼模型的自振特性

为确定该矿办公楼模型的自振特性，研究应用ANSYS软件，采用子空间迭代方法计算获得模型的频率对办公楼模型进行了模态分析，并提取了结构前40阶频率，由频率和周期的对应关系，得到办公楼结构的自振周期如图6所示。

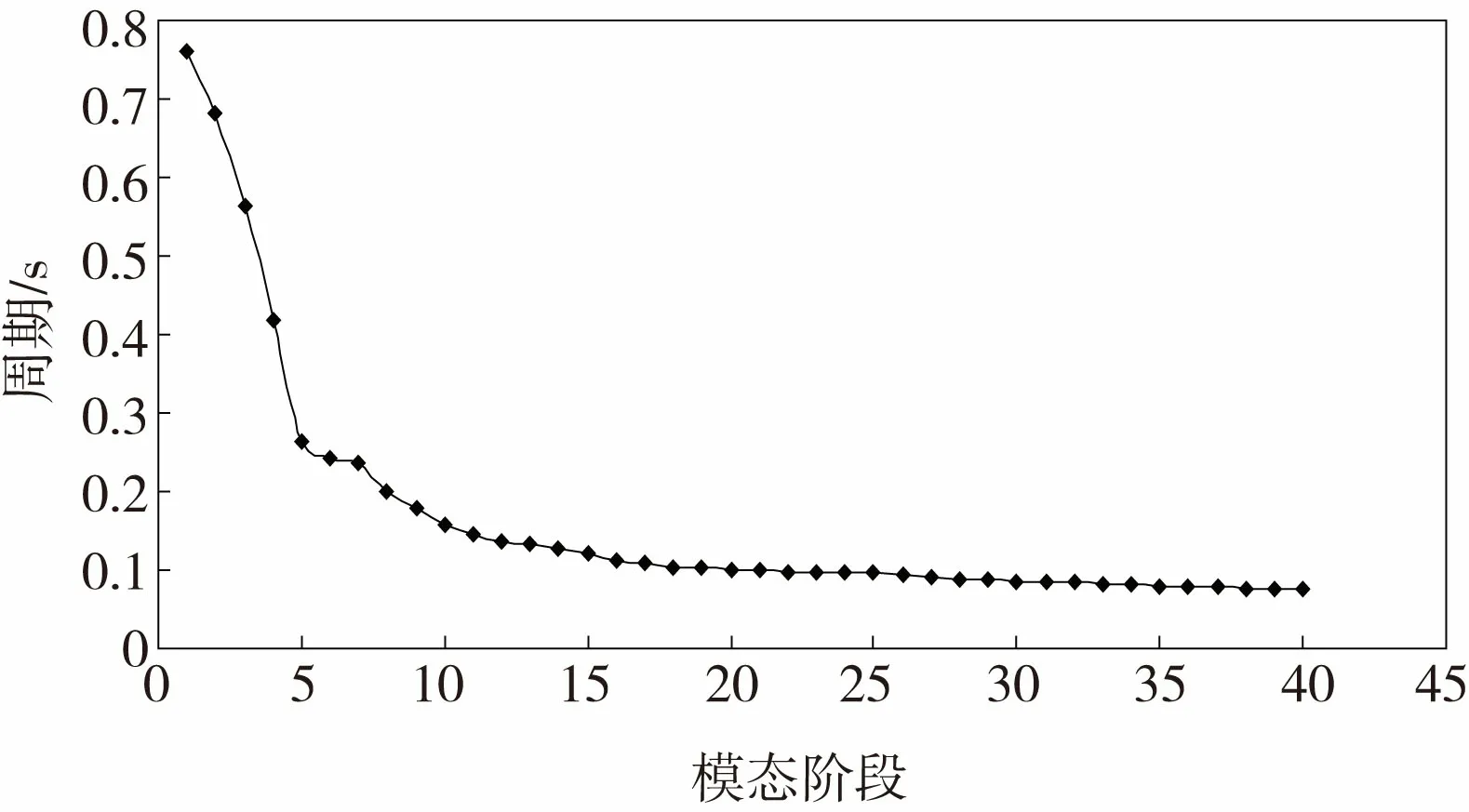
图6 结构自振周期随阶数变化曲线Fig.6 The curve of natural vibration period with order of structure

从图6可知，结构前四阶自振周期逐步下降，第五阶至第七阶自振周期较接近，7阶以后自振周期逐渐变短，第16阶自振周期以后趋于平稳变化，阶数越大，自振周期缓慢变短。其中，模型的高阶振型出现扭转效应。

2.3 爆破振动作用下办公楼振动响应

2.3.1 动力响应时程分析

根据在进行动力响应时程分析时，采用NEWMARK-β法进行数值积分，迭代求解。为提高迭代精度，保证迭代收敛性，将地震波或震动波记录的时间间隔0.125 s，改为取迭代步长为0.0125 s；在加载过程中采用逐级加载的方法进行加载。

在进行动力响应时程分析时，鉴于结构阻尼对结构的动力响应影响很大，阻尼比的影响基本上反比于位移反应。因此，在选取阻尼时，采用输入Rayleigh阻尼(瑞利阻尼)的方法。即选取瑞利阻尼为：

C=αM+βK

(3)

式中：C为动力方程中的阻尼矩阵，K为刚度矩阵，M为质量矩阵，α为与质量成比例的阻尼常数；β为与刚度成比例的阻尼常数，αM为质量分量，βK为刚度分量。α、β可由公式(4)确定，即：

(4)

式中：ϖi、ϖj分别为结构第i、j振型的圆频率；ξi、ξj为结构第i、j振型的阻尼比。对于混凝土结构，两个振型假设具有相同的阻尼比ξi=ξj=0.05。通过模态分析提取了结构的频率ω，根据式(4)，然后可以确定阻尼参数α和β。

2.3.2 爆破振动作用下的结构加速度、速度、位移时程曲线分析

由于篇幅的原因加速度、速度时程曲线省略，分析过程三者基本相同，此处仅以位移时程曲线为例进行了分析。结构受爆破振动水平径向加速度作用，在0.875 s时刻(爆破振动水平径向最大加速度时刻)结构顶层的位移时程曲线如图7、8所示，结构径向位移和切向位移最大值分别为1.59×10-6m和2.17×10-6m。

图7 水平径向结构顶层位移时程曲线Fig.7 The top displacement time-history curve of the horizontal radial direction structure

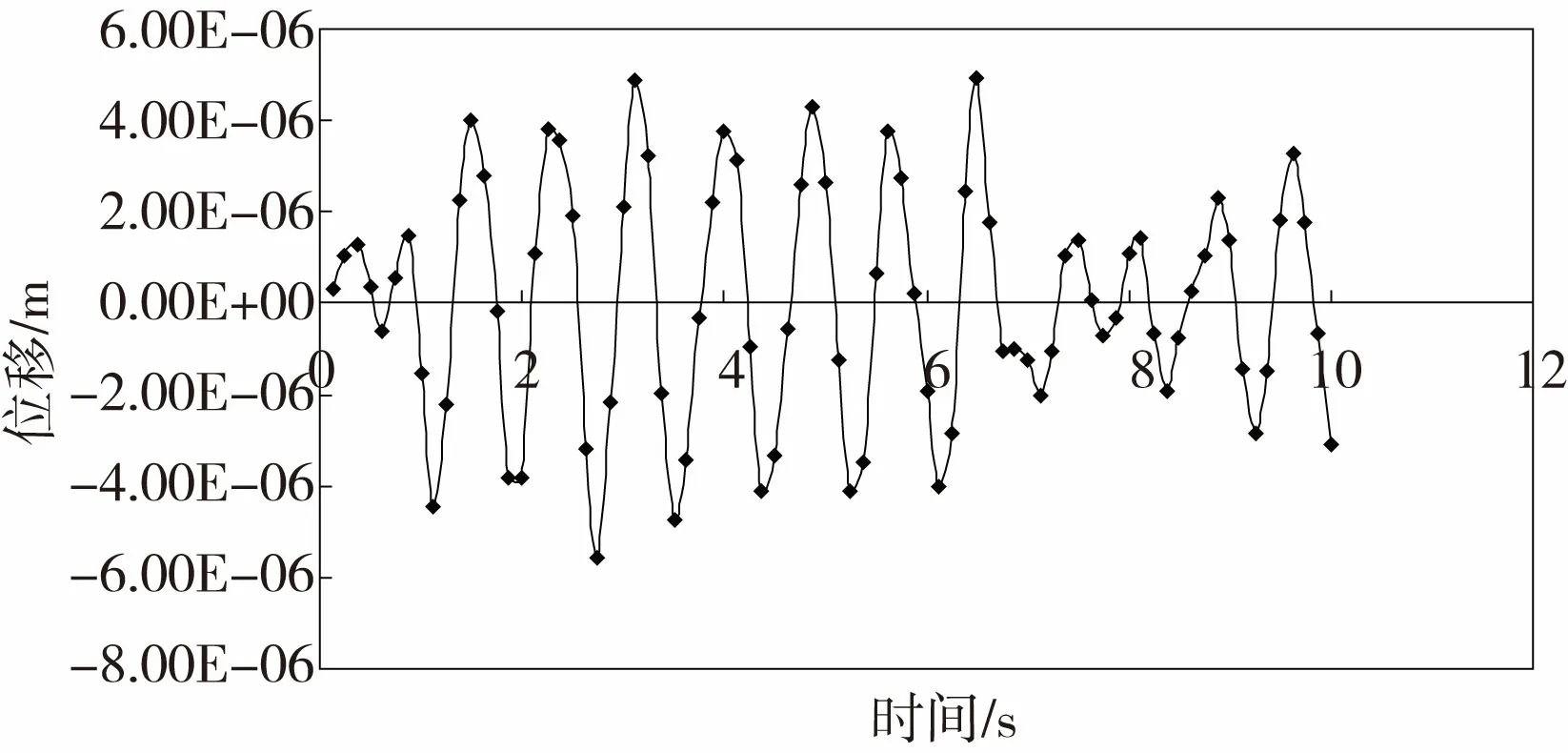
图8 水平切向结构顶层位移时程曲线Fig.8 The top displacement time-history curve of the horizontal tangential direction structure

结构受爆破振动水平切向加速度作用，在9.25 s时刻(爆破振动水平切向最大加速度时刻)结构顶层的位移时程曲线如图9、10所示，结构径向位移和切向位移最大值分别为2.21×10-6m和1.55×10-6m，均小于最小安全值。

图9 水平径向结构顶层位移时程曲线Fig.9 The top displacement time-history curve of the horizontal radial direction structure

图10 水平切向结构顶层位移时程曲线Fig.10 The top displacement time-history curve of the horizontal tangential direction structure

结构受爆破振动垂直加速度作用，在5 s时(爆破振动水平切向最大加速度时刻)结构顶层的位移时程曲线如图11所示，结构垂直位移和切向位移最大值为4.92×10-6m。

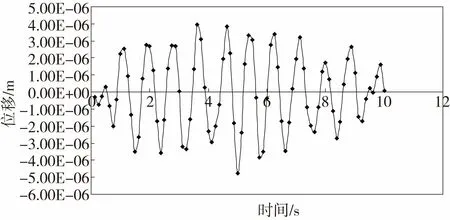
图11 竖直方向结构顶层位移时程曲线Fig.11 The top displacement time-history curve of the upright direction structure

通过对爆破振动作用下办公楼受爆破振动各个方向上最大加速度作用下结构顶层的加速度、速度和位移的时程曲线进行分析，得出最大值，均小于安全值。

通过对加速度、速度和位移时程曲线分析，可以对加速度、速度和位移随时间的变化过程有一个充分的认识和理解，通过对其分析可以对框架结构建筑物对爆破震动波的响应过程有一个更清晰的认识。

3 办公楼结构动力响应程度分析

在二采区开采爆破时所监测的办公楼1楼振动波速(水平切向)作用下，计算的监测点处响应加速度时程曲线如图12所示。

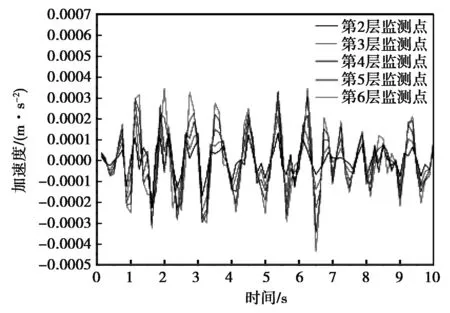
图12 二采区开采爆破时计算的监测点处响应加速度时程曲线Fig.12 Response time curves of monitoring points at the time of blasting in the two mining areas

根据结构动力响应规律，常定义加速度放大系数η为结构加速度动峰值与结构基础加速度动峰值的比值。因此，如果结构体内任意一点E的动力响应的加速度峰值为aE，基础处的动力响应的加速度峰值为a，则E点的加速度放大系数η可用式(5)表示，即有：

(5)

由图12和式(5)可得办公楼2层、3层、4层、5层、6层对应监测点处的加速度放大系数，如表1所示。

由表1可知，除2层对应监测点处的爆破振动响应加速度缩小外，其余楼层对应监测点处的爆破振动响应加速度均放大。3层、4层、5层、6层对应监测点处的爆破振动响应加速度放大系数分别为26%、17%、34%和69%。但各楼层对应监测点处的爆破振动响应加速度均较小，最大值均未超过6.00×10-4m/s2。

表1 结构相关部位加速度放大系数一览表(有阻尼)Table 1 List of acceleration magnification coefficients for structure related parts (damping)

二采区开采爆破在办公楼引起的振动响应总体较小，对办公楼整体稳定性基本无影响。除2层对应监测点处的爆破振动响应加速度缩小外，其余楼层对应监测点处的爆破振动响应加速度放大效应并随着楼层的增高逐渐增大的趋势，6层放大效应达到最大。

4 结论

1)在二采区开采爆破振动作用下，办公楼结构前4阶自振周期逐步下降，第5阶至第7阶自振周期较接近， 7阶以后随着阶数越大自振周期逐渐变短，第16阶自振周期以后趋于平稳变化，模型的高阶振型出现扭转效应，使得整个建筑物的安全性和稳定性都大幅下降。

2)通过对爆破振动作用下办公楼受爆破振动各个方向上最大加速度作用下结构顶层的加速度、速度和位移的时程曲线进行分析，得出最大值，均小于安全值。通过时程曲线可以对加速度、速度和位移进行分析，从而为判断建筑物的安全性提供一定的参考。

3)除2层外框架结构对矿山爆破的加速度放大效应随楼层有逐渐变大的趋势，顶层的加速度放大效应最大。因此，矿山爆破对大于2层框架建筑物有影响，应加强对顶层的监测。对于2层加速度的放大效应出现异常变小现象，需要做进一步研究和分析。