普通克里格法在铜曼矿区储量估算中的应用
2019-03-07刘佶林王孝东冯光华
刘佶林,杨 忠,王孝东,冯光华
(1. 云南华联锌铟股份有限公司,云南 文山663701;2. 昆明理工大学 国土资源工程学院,昆明650093)
目前,我国矿山在进行资源储量估算时,普遍采用块段法和剖面法等传统储量估算方法[1]。数字矿山技术的运用,首次实现了对开采矿体的规模、形态、品位等属性在空间分布上的数字化整体描述。近年来,诸如3DMine、DIMine、Surpac等三维矿业软件的推广与应用,使得利用地质统计学方法进行资源储量估算已成为国内外资源评估的重要手段。
云南都龙铜街曼家寨锡锌多金属矿区(以下简称铜曼矿区)位于云南省东南部,矿区面积约5 km2。矿区北部和东部以F0断层为界,宽约1.5 km。矿区南面延伸至中越国境线,长约8 km,构成南北向展布的锡、锌、铜、银等多金属矿带[2]。矿体走向近南北,向西倾斜,倾角为10°~40°,局部倾角高达60°。矿区具有叠瓦状排列、分支复合、尖灭再现的特点,随含矿层同步褶曲。铜曼露天采场内地形地质情况复杂,矿岩交错分布,小矿体数量较多,矿体边缘部夹石和夹矿现象明显,如何充分利用大量的原始勘探数据和矿山生产的地质编录数据进行储量估算对矿区的矿产资源评估与矿山开采方案制定具有重要的意义。
1 三维地质模型构建
1.1 地质数据库
地质数据库是进行地质解译、块体品位估值、储量估算等工作的重要基础[3],本次研究基于3DMine三维矿业软件,充分利用各勘探时期的勘探成果和生产勘探资料,共计738个钻孔和78条探槽数据,建立了三维地质数据库,如图1所示。三维地质数据库的建立可将数字形式的勘探资料用三维图形形象化、具体化,便于管理和分析利用。在地质数据库中可以用三维显示方式浏览所有钻孔的基本信息,显示单个或多个工程的地质品位、深度、轨迹等数据信息,还可根据需要设置不同的显示风格来查看钻孔的空间分布情况。
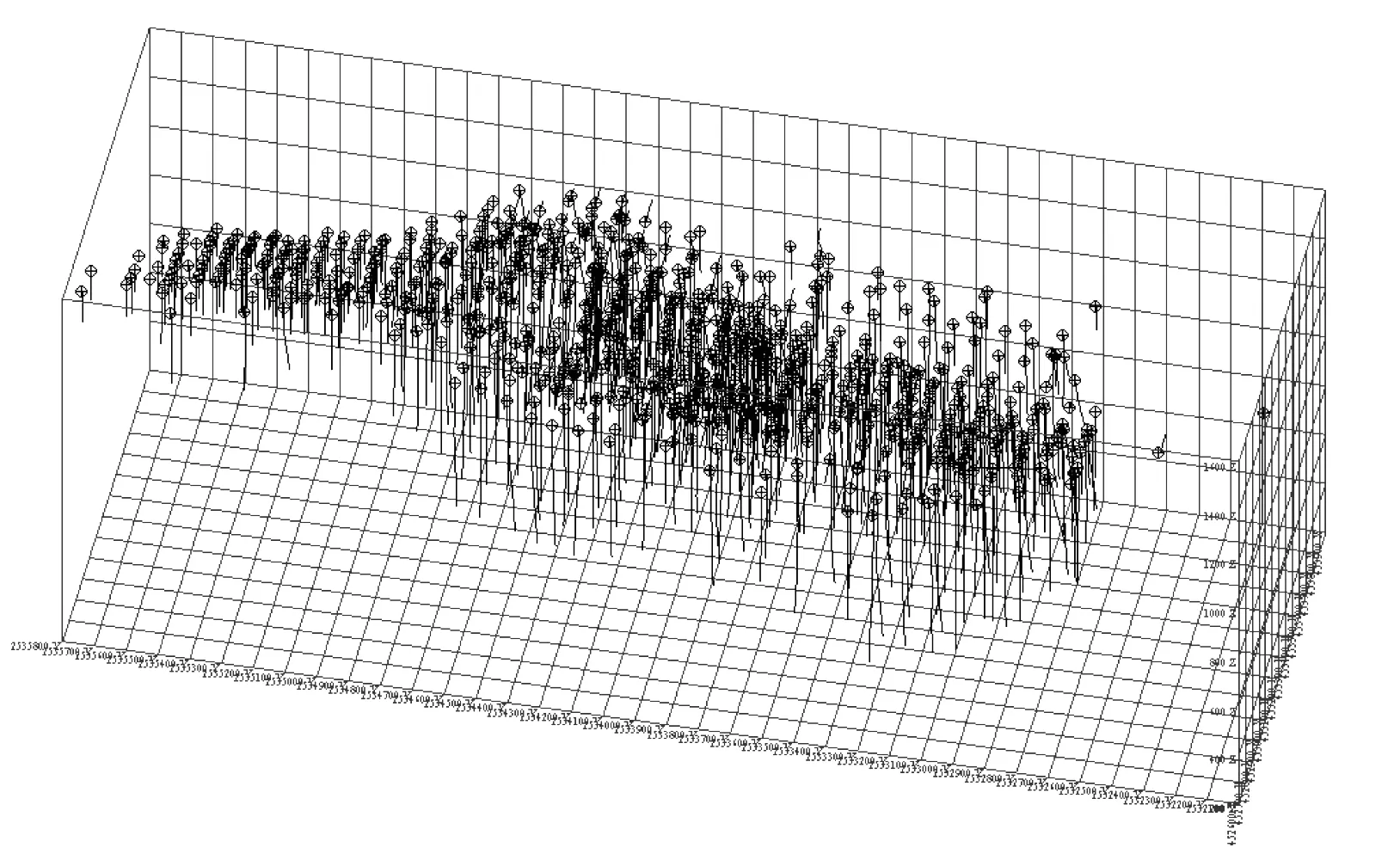
图1 三维地质数据库Fig.1 3D geologic database
1.2 矿体模型
矿体(实体)模型,是在三维空间内由一系列剖面或空间点构成的三角网包裹成封闭的实体,最直接的作用就是模拟矿体形态。本次研究利用3DMine三维矿业软件,以铜曼矿区三维地质数据库(如图1所示)为基础,按照矿体圈定原则对矿区进行了地质解译,圈连矿体(实体)模型四百余个(如图2所示)。

图2 矿体模型Fig.2 The ore body model
1.3 块体模型
利用上述方法建立的矿体模型,矿体内部是空的,没有任何信息。为了便于后期储量计算、境界设计等工作,需要在不规则的矿体内部以及周边小部分范围内填充规则的三维等块状模型(块体),这种块体集称为块体模型。块体模型是品位估值和储量估算的基础,也是大多数数学优化方法的基础。目前的露天开采规划优化方法、储量计算、境界设计、采剥计划编制等,几乎都是以块体模型作为研究手段。块体模型可根据生产需要添加诸多属性,如矿体编号、经济类型、矿石品位、矿石体重、矿岩类型等,便于在生产实践中随着已知信息量的增加或变化不断更新属性信息。考虑到块体边界与矿体范围的吻合度越高,块体所反映的空间位置与矿体更趋近于一致,因此采用次级模块的方法对原始块体进行分割,然后利用已知组合样品点对整个矿体范围内的单元块的品位进行估计,并在此基础上进行储量估算。

图3 块体模型Fig.3 The block model
2 储量估算
一般来说,在三维矿业软件中,利用三维地质模型和克里格法进行储量估算的主要步骤[1]如图4所示。
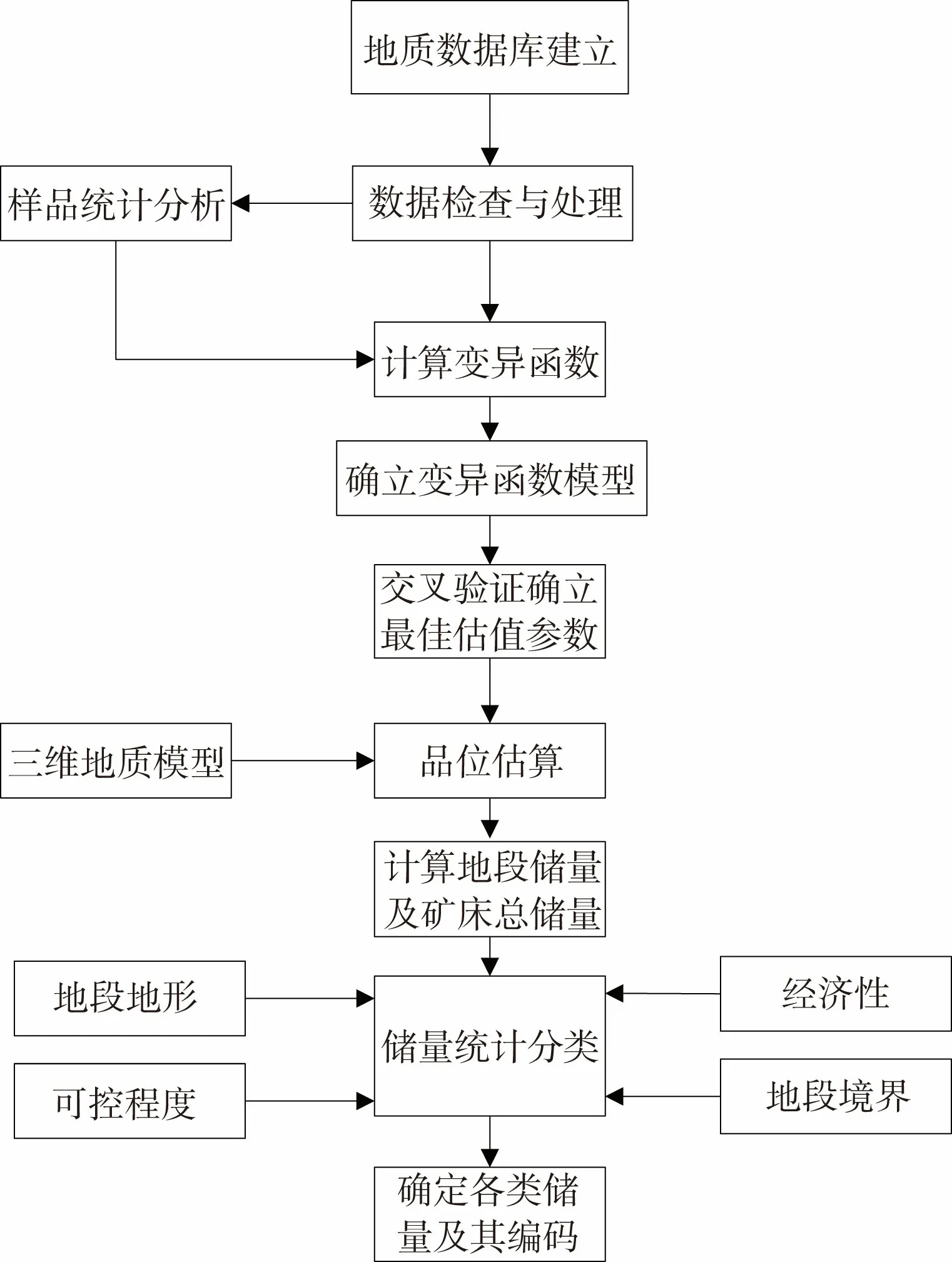
图4 储量估算基本流程Fig.4 The basic flow of reserve estimation
2.1 区域变化量选择
应用地质统计学进行储量计算时,须根据矿床的具体情况和特点以及所采用的方法、手段来选取区域变化量[4]。由于铜曼矿区矿体形态复杂,矿岩交错现象明显,矿体形态、走向、倾向、厚度变化较大,故本次研究先根据勘探线剖面把矿体的实体模型确定下来,再利用克里格法对所圈定的矿体进行品位估值,本次研究主要选择品位值作为区域变化量。
2.2 基本统计
在对块体模型进行品位估值之前,要结合矿床的成因对矿区样品的品位分布特征进行统计分析,为后续的品位估值提供数据基础,以便根据矿床自身特点选择适当的估值方案[5]。利用3DMine软件中的地质统计学模块对铜曼矿区的样品点进行统计分析,研究样品点数据的分布特征,如数据不符合正态分布则进行变换。本次研究主要分析铜曼矿区的Zn元素,统计结果如表1和表2所示。
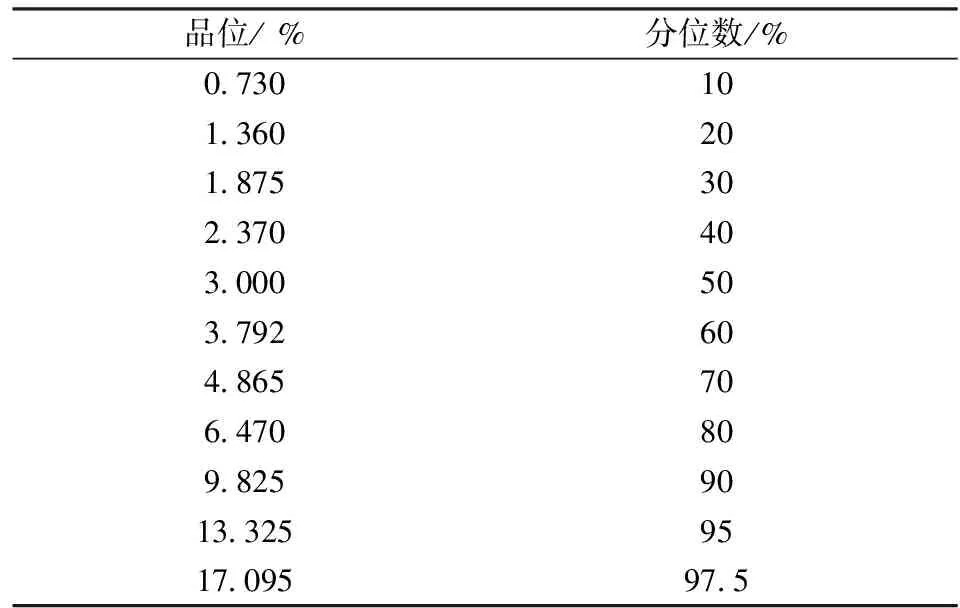
表1 Zn元素样品点分位数统计Table 1 Quantile statistics of Zn samples

表2 Zn元素样品点基本统计Table 2 The basic statistics of Zn samples
统计分析的主要目的是确定矿区Zn元素样品点的分布类型,为随后的变异函数计算及Zn品位估值提供参考。
从图5(a)可以看出,Zn元素样品点不服从正态分布,故将Zn样品点进行对数转换,使其服从正态分布,如图5(b)所示。由于Zn元素样品点存在一些特高品位,因此必须对特高品位进行处理。本次特高品位处理参照矿区储量核实报告,对超过矿床平均品位8倍的特高品位,采用工程平均品位代替。
2.3 样品组合
地质统计学要求参与估值计算的数据的支撑(指样品的长度或体积)应该一致[6],因此样品组合就是要将探矿工程中的样长和品位值量化到离散点上,即每段样长的中点,只有在工程方向上产生均匀(即等距离)的离散点才能用于资源储量估算[7]。因此,样品组合产生的离散点将用于块体模型估值。
根据样品的统计分析,其原始平均样品长度为1.21,绝大部分样品的样长在1 m左右。因此,本次研究采用等距离为1 m的样品长度进行计算分析,最小组合样长为平均样长的50%,即0.5 m。
2.4 变异函数模型
由于变异函数计算直接影响到变异函数的拟合及克里格法估值的精度[8-9],因此变异函数是克里格法储量估算的重要组成部分。地质统计学中拟合各向异性的基本思路是求三个相互垂直方向(主轴、次轴、短轴)的变异函数,这三个方向上的变程的比值就是各向异性中轴的比例。通常,对于大多数金属矿床,可以根据矿体走向、倾向、厚度进行变异函数的分析。本次研究在3DMine软件中对Zn元素样品进行走向(主轴)、倾向(次轴)、厚度(短轴)3个方向的实验变异函数计算。结合铜曼矿区勘探工程间距为80 m×80 m的实际情况,在计算实验变异函数时的基本滞后距离取勘探工程的1/2(即40 m),滞后距误差限为勘探工程间距的1/4(即20 m),变异函数计算方向如表3所示。
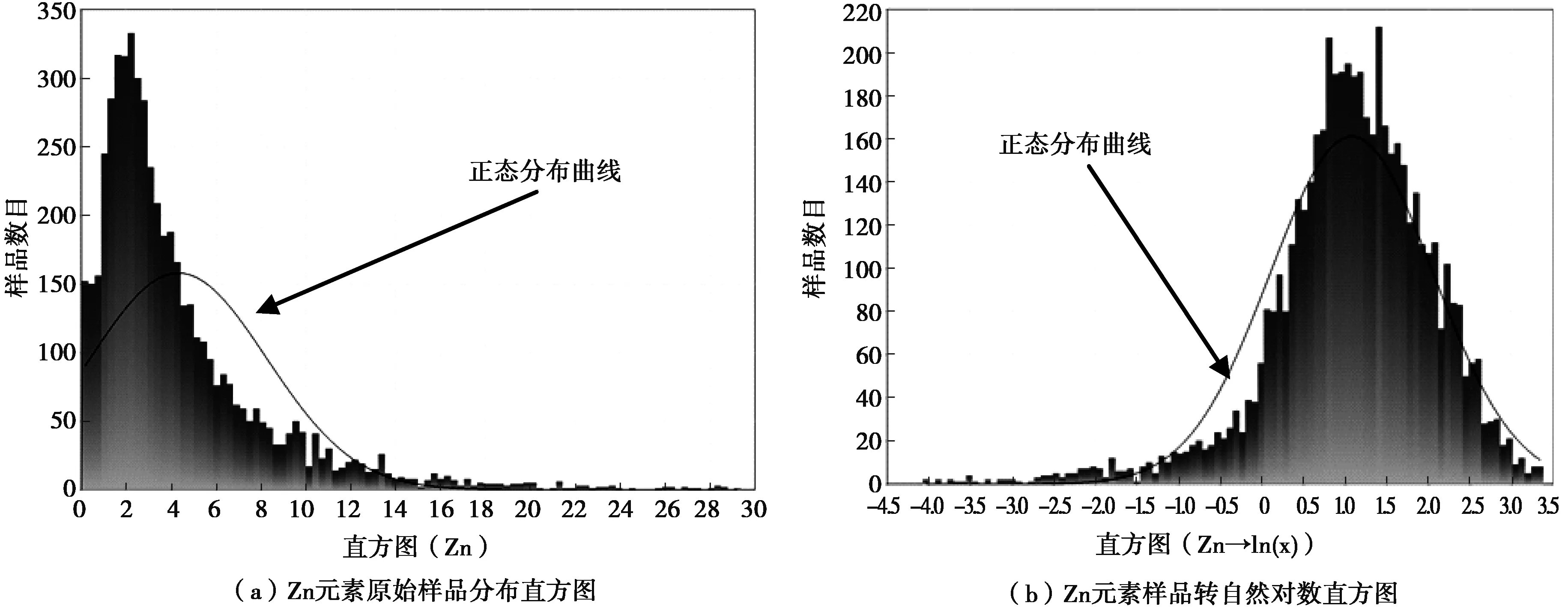
图5 Zn元素原始样品分布直方图Fig.5 The original sample distribution histogram of Zn samples
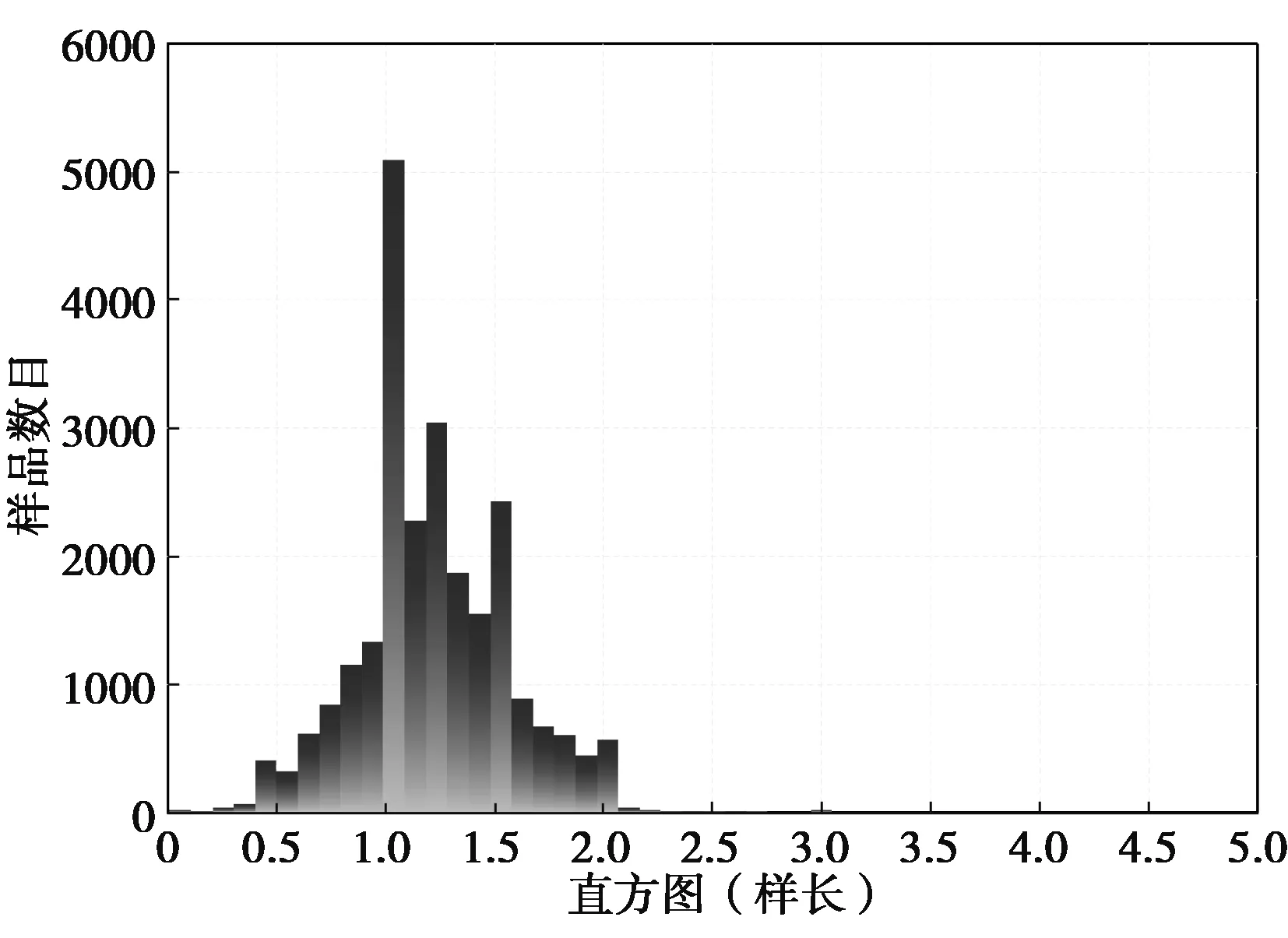
图6 铜曼矿区全部样品点样长统计Fig.6 The point sample length statistics total samples of Tongman mine表3 Zn元素品位变异函数计算方向Table 3 The calculation direction of variation function for Zn samples
由于Zn元素样品点在各个方向上的影响半径各不相同,因此需要找到每个方向上影响距离的比率,即各向异性。在3DMine软件地质统计模块中,双击主轴函数图,选择模型中的“指数模型”进行拟合。调整指数模型曲线上的红点,使指数模型的曲线与变异曲线尽可能形态一致,调整完主轴后再依次调整次轴和短轴。
调整曲线的过程中,右侧变异函数参数及各向异性参数都在发生变化。根据经验判断一个合理的变异函数的基本原则是,随着距离增大,伽玛值(Gamma)不断上升,变程也越大。在所有扇区中选择一个最符合正态分布的方向设为“主变异函数方向”,即搜索椭球体的主轴,如图7所示。
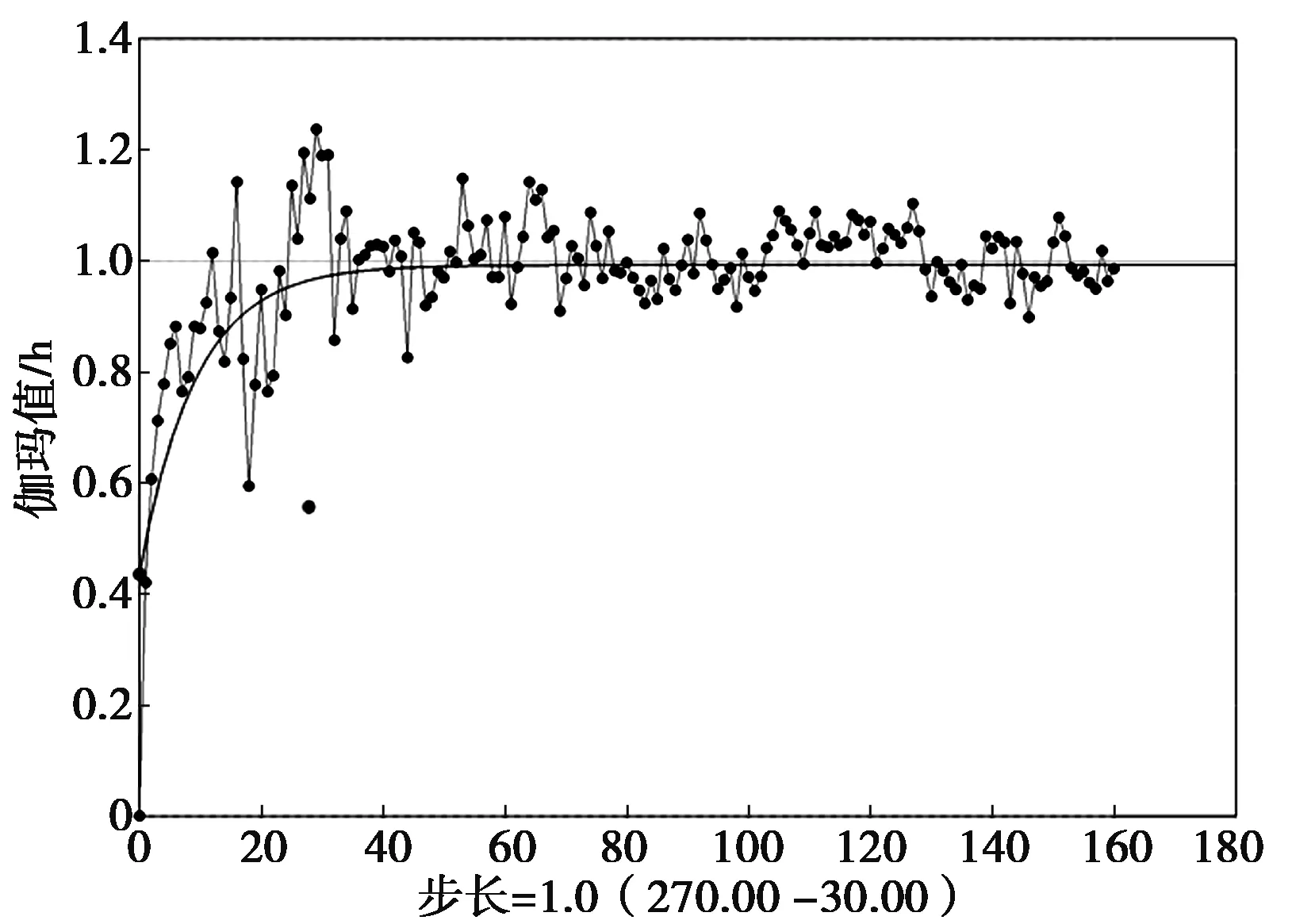
图7 Zn品位主轴(走向方向)变异函数曲线Fig.7 The variation function curve of main axial for Zn grade
主轴确定后,在垂直于主轴的方向上将生成一个平面,该平面分为8个扇区,在这8个扇区中,又以相同的方式,找到一个最符合正态分布的方向并确定为次轴变异函数方向,如图 8所示。
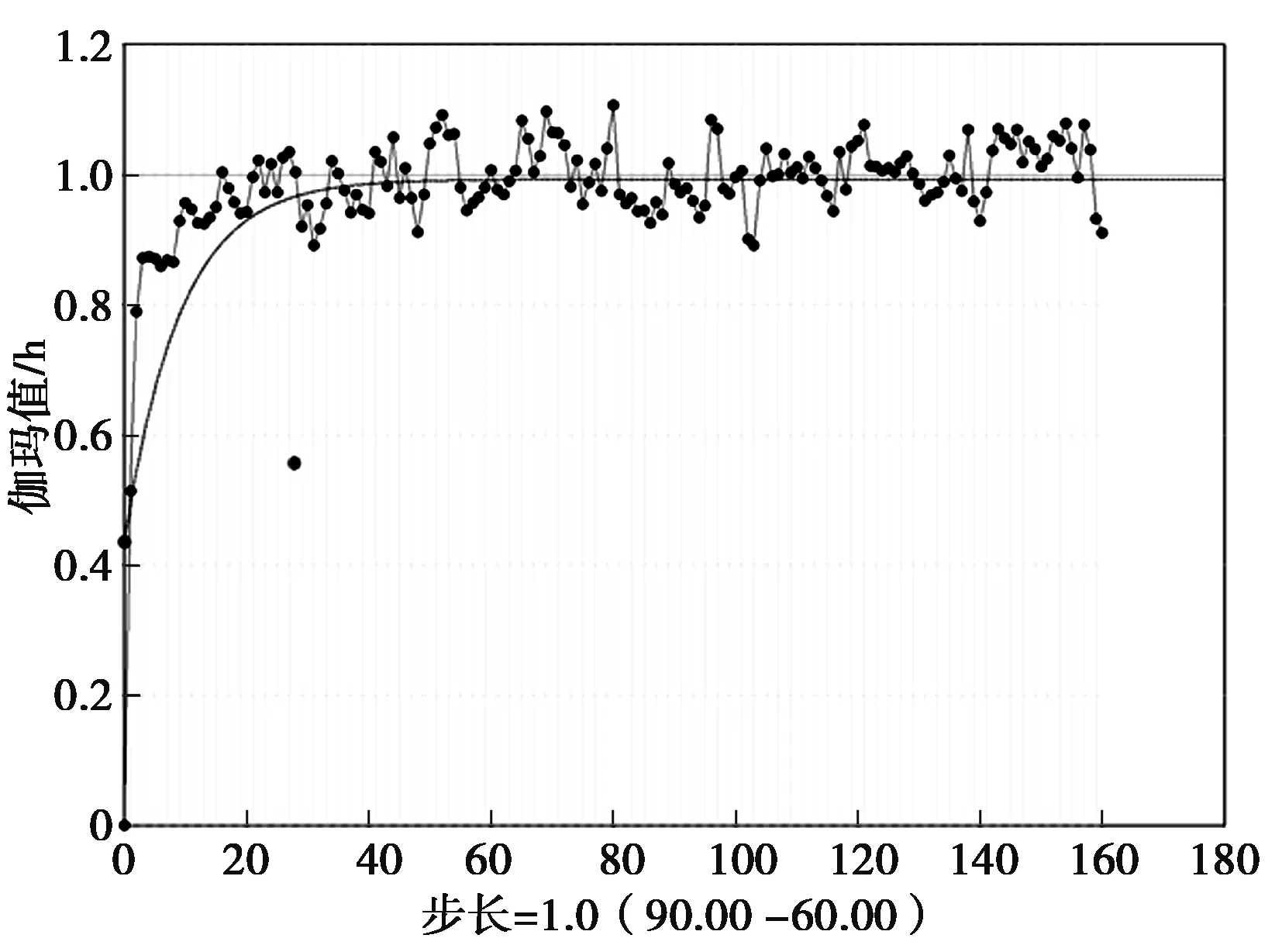
图8 Zn品位次轴(倾向方向)变异函数曲线Fig.8 The variation function curve of secondary axial for Zn grade
当确定主轴和次轴方向后,短轴方向将自动确定,如图9所示。
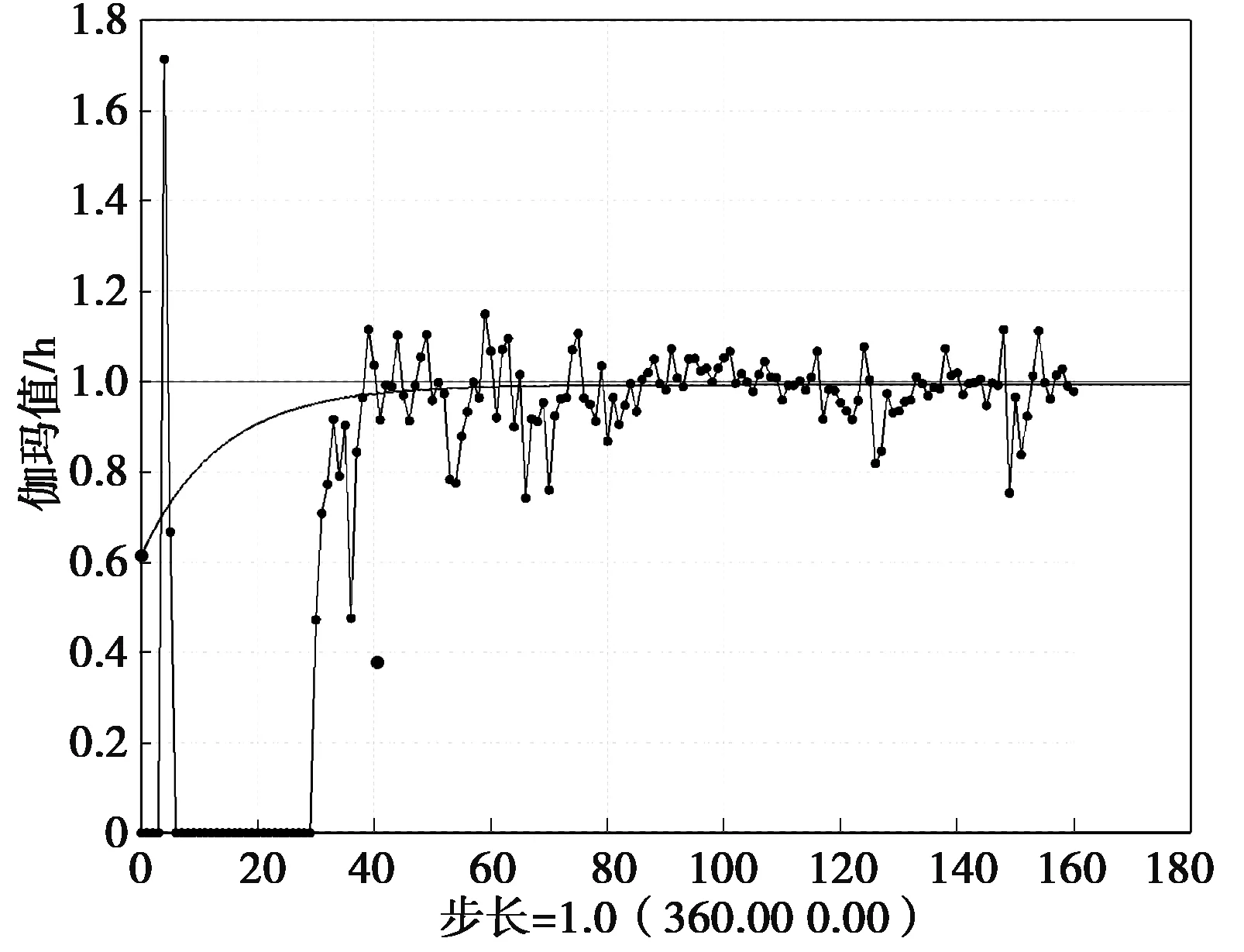
图9 Zn品位短轴(厚度方向)变异函数曲线Fig.9 The variation function curve of short axial for Zn grade
拟合完毕后,将此工程保存起来,计算获得的参数将用于为Zn品位模型估值。拟合结果如表4所示。

表4 Zn元素理论变异函数拟合参数Table 4 The fitting parameters of variation function for Zn samples
变异函数的拟合参数主要有块金值、基台值和变程。其中,块金值由于变量空间分布的不均匀性和测量误差的存在,在最小采样尺度下变量的变异性,可反映出区域变化量随机性的大小。基台值表示变量在空间中的总变异性,即h大于变程时变差函数的返回值。变程是指区域变化量在空间上具有相关性的范围。在变程范围之内,数据具有相关性,但在变程之外,数据之间的相关性减弱直至消失,用超出变程之外的数据对未知点进行估值等同于数学平均。
理论变异函数参数将用于估算块体模型中的Zn品位,这对Zn品位估值的准确性有很大的影响。因此,在估值前应当对变异函数的参数进行交叉验证,即对应用这些参数进行品位估值时的可靠性进行初步判断[10]。理论变异函数参数的可靠性通常基于以下两个方面的交叉验证结果来判断[11]:
1)交叉验证的原始均值和估计均值趋于相等,交叉验证的误差均值应趋近于0。
2)误差方差和误差平均值趋于相等且尽可能小。
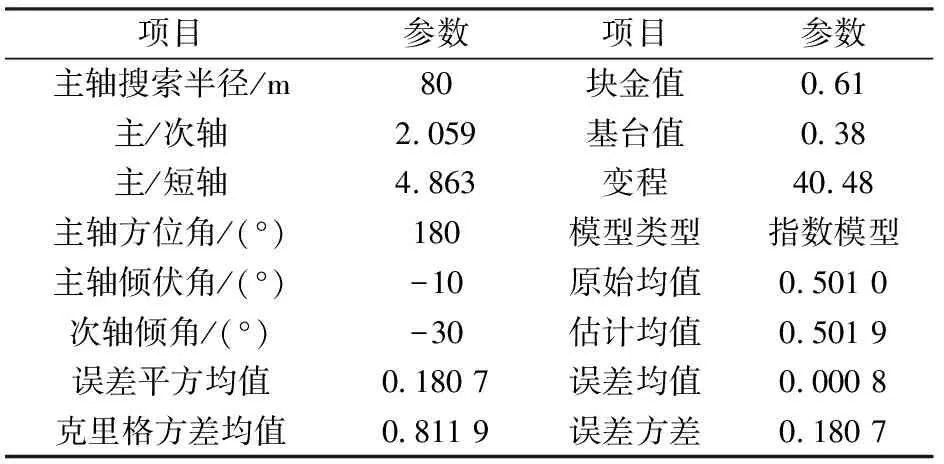
表5 交叉验证表Table 5 Cross validation Table
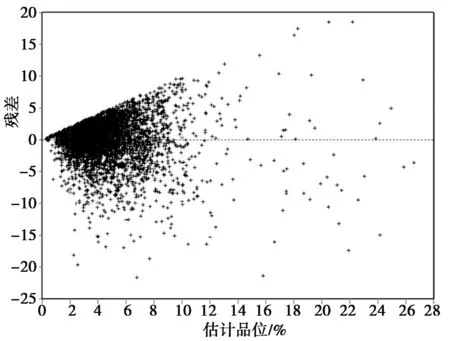
图10 Zn元素样品点估值的残差图Fig.10 The residual chart of Zn samples’ estimation
从表5可以看出,原始均值0.501 0与估计均值0.501 9之差趋于0,误差平方均值0.180 7和误差方差0.180 7相等,说明所选的Zn元素品位模型结构模型较好,变异函数拟合科学合理。从图 10可看出,Zn元素的大部分样品点的散点品位1%~8%,且分布在残差0线(虚线)附近,说明残差值较小,与2.2节中Zn元素的样品点分位数区间统计结果相吻合,故可以获得较好的估值效果。
2.5 搜索椭球体
搜索椭球体是一个代表各向异性的体,它与待估块体的中心重合。一般情况下,椭球体的长轴方向与矿化域走向一致,次轴和短轴则分别与矿化域的倾向方向和厚度方向一致[1]。搜索椭球体的大小由各个轴向的直径决定,而各个轴向的直径由两个因素决定,即与待估块相邻的最近工程之间的距离和矿化域各个方向的变异性。
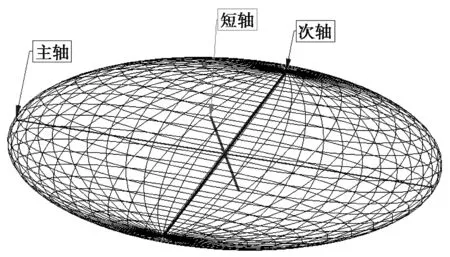
图11 椭球体示意图Fig.11 Schematic diagram of ellipsoid
结合铜曼矿区矿体形态特点、变异函数模拟结果,搜索椭球体参数设置如表6所示。
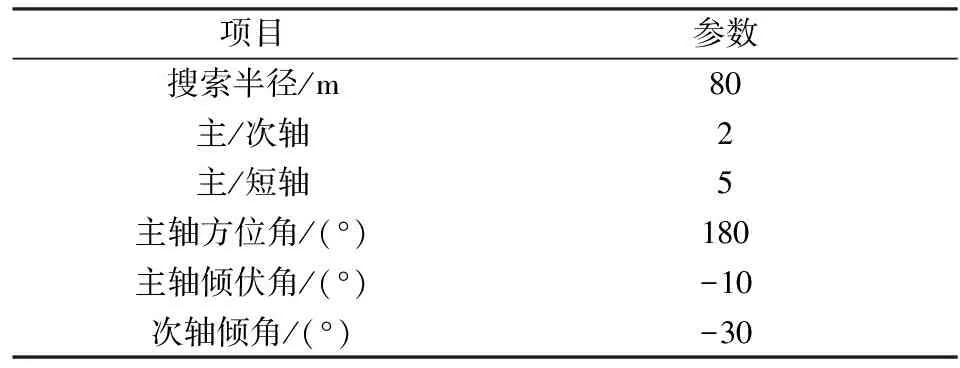
表6 搜索椭球体参数Table 6 Ellipsoid’s parameters
2.6 克里格法
1951年,Krige提出了一种为样品点赋值,让块体品位成为样品分析结果的线性组合,使样品分析结果与权重渐近的方法,1963年Matheron将这种渐近的估值方法概括命名为“克里格法”[12]。一般来说,克里格法是一种寻求最优、线性、无偏内插值估计的方法。它是在考虑了样品信息的大小、形状与待估值点之间的空间分布位置等特征以及区域化变量的空间结构信息的前提下,给每个样品值分别赋予一定的权重系数后,用加权平均法评估待估值点的方法[13]。克里格法是一个获得未知变量的估计方差最小化(最佳线性无偏估计)的随机过程。克里格法估值中,普通克里格法是资源储量估算中较为常用的方法[1]。普通克里格法的估算公式如下:
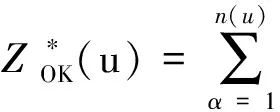
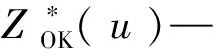
克里格法估值参数如表7所示。
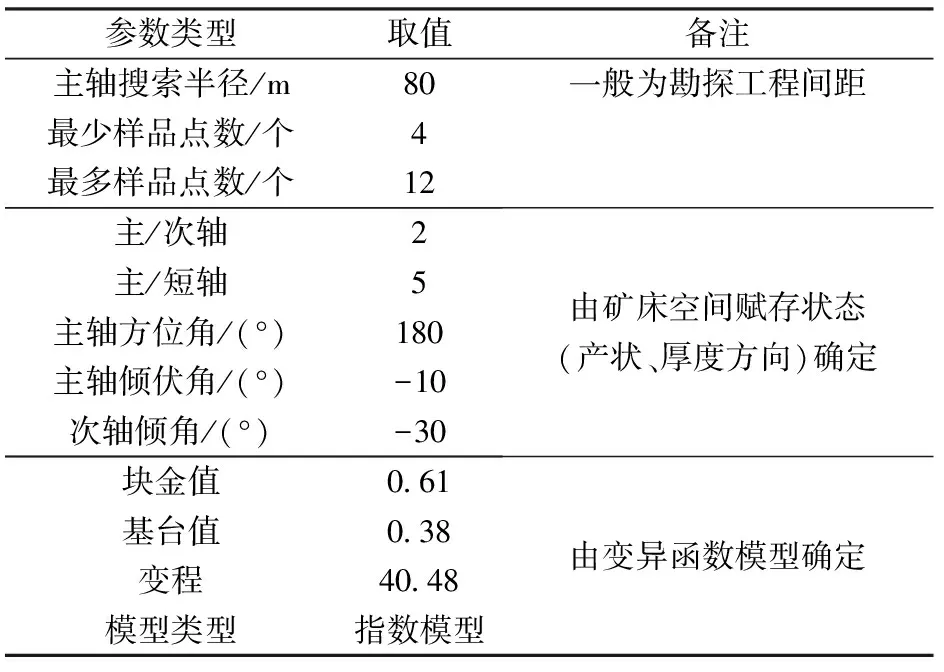
表7 克里格法估值参数Table 7 Estimation parameters of Kriging
2.7 估值结果
应用普通克里格估值法对铜曼矿区进行储量估算,截至2016年末,铜曼矿区内工业矿石共计7 979.50万t,平均Zn品位4.19%。为验证估值结果的可靠性,将普通克里格法的储量估算结果与传统储量估算结果进行对比,对比情况如下。
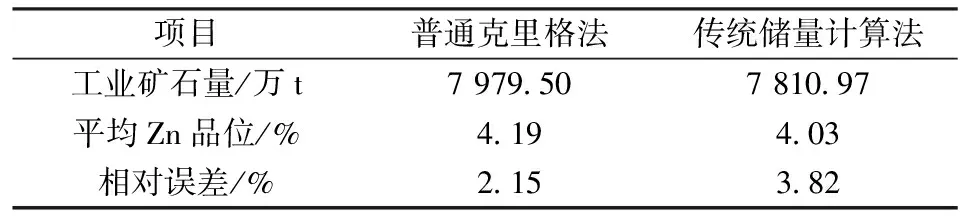
表8 普通克里格法与传统储量计算法估值结果对比Table 8 Estimation results comparison between ordinary Kriging and traditional method
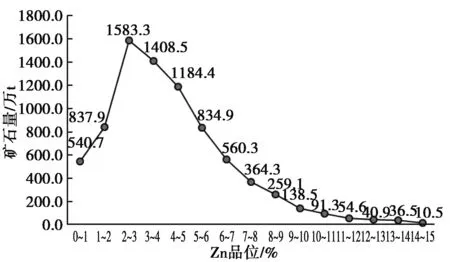
图12 Zn元素品位—矿石量曲线图Fig.12 Grade-reserves curve diagram of Zn samples
由表8可看出,普通克里格法的储量估算结果与传统储量估算结果相对误差在合理范围内,无显著性差异。从图12可看出,普通克里格法的估值结果中Zn元素的品位—矿石量曲线图与图5(a)中Zn元素样品点分布规律图基本吻合,说明克里格法估值结果可靠。
3 结论
本文基于3DMine三维矿业软件,对铜曼矿区建立了三维地质模型,阐述了普通克里格法储量估算应用过程中样品点统计、参数的选取、变异函数拟合、椭球体参数的确定过程。利用普通克里格法对铜曼矿区矿体储量进行了估算,估算结果表明基于3DMine软件的普通克里格法储量估算结果相对准确,可以作为矿山资源储量管理和开发利用的依据。此外,普通克里格法估算方法能充分利用样品信息,相比传统的手工计算方式,可提高工程技术人员工作效率,值得推广应用。
