降雨条件下含裂缝的边坡数值模拟分析

李全文，常金源，，徐文刚，杨 成

(1.绍兴文理学院，浙江 绍兴 312000；2.浙江省工程勘察院，浙江 宁波 315012；3.华东勘测设计研究院有限公司，浙江 杭州 311122)

降雨型滑坡的特点与降雨过程联系密切，而降雨过程中雨水的入渗和在坡体中的渗流是决定滑坡稳定性的主要因素。对于降雨敏感的滑坡，水在边坡稳定性评价中具有关键性的作用。水会使得组成边坡的岩土体物理力学指标弱化。这种弱化现象由两部分组成，一是改变岩土体的力学性质，如c、φ值的降低，二是改变了岩土体的力学状态，如孔隙水压力(u)的增高降低了有效应力(σ′)的水平。

对于均质完整的土质斜坡，雨水入渗和坡体内渗流均通过斜坡表面的非饱和、饱和渗流完成。如果由于土质斜坡的不均匀变形，在坡表出现了拉张裂缝，因为裂缝可以看作比组成坡体的土体渗透系数大很多倍的“物质”[1]，则雨水入渗会优先沿着这些后天生成的裂缝形成集中的渗流，这些裂缝成为了优势入渗通道。此时降雨入渗将表现出裂隙流和表面渗流的双重特点。

我国东南沿海丘陵地区，坡体表层由于风化作用，多形成松散堆积的残坡积层，在降雨影响下多形成浅层滑坡。此类滑坡的深长比小，分析时常将其作为无限平面滑动型滑坡来研究。如Skempton等[2]建立了平行于坡表的无限边坡模型，并求取了边坡的稳定性安全系数(Fs)表达式；Pradel等[3]将南加利福尼亚作为研究区域，研究了均质边坡在长历时、高强度降雨条件下的浅层滑坡现象，建立了无限平面滑动型边坡模型。本文即以此类型滑坡作为研究对象，建立无限平面滑动型滑坡模型，进而分析评价降雨过程中裂缝对滑坡稳定性的影响。

1 基本原理

1.1 表面入渗的一般过程

1.2 裂隙入渗

降雨过程中，地表径流灌入滑坡后缘裂隙，裂隙中产生静水压力作用。裂隙渗流属于有压入渗，初始入渗压力远远大于表面入渗，因此，其扩展范围也就较之增大。

表1 土性参数[7]

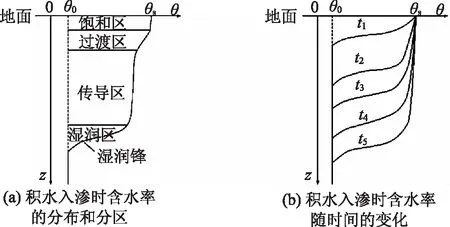
图1 积水入渗时含水率的变化情况

软件中可以用总水头边界条件来模拟裂缝入渗的情况。总水头由压力水头和高程组成，其中高程代表重力分量，数学表达式如式(1)所示[5]。由于裂隙表面的水压力由上到下呈静水压力状态分布，因此用总水头边界用来模拟裂隙中存水时的渗流情况是合适的。与此相对应的是坡面入渗选择压力水头边界，两者之间的差异如图2所示。

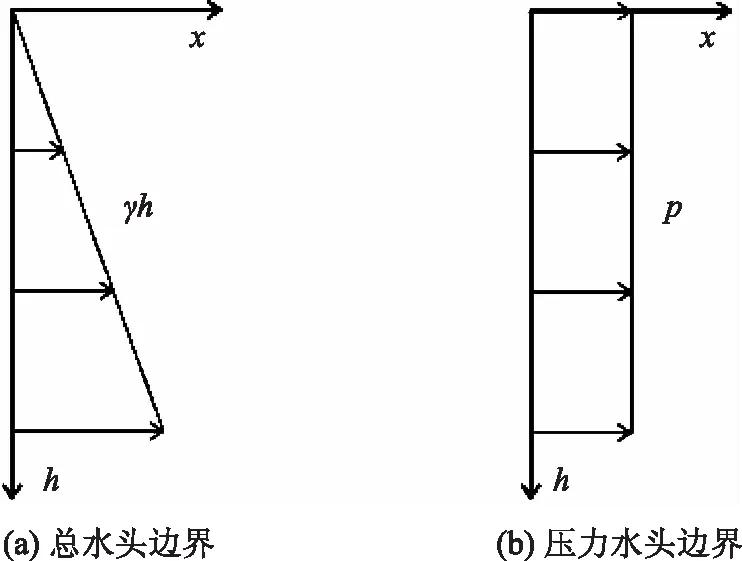
图2 总水头边界和压力水头边界比较

(1)

式中，H—总水头，m；u—孔隙水压力，kPa；rw—水的容重，kN/m3；he—高程，m；u/rw—压力水头，采用长度单位，m。

2 土性参数与模型设计

2.1 土性参数

模型采用粉土，其土性参数见表1，土水特征曲线(Van Genuchen拟合方程[6])和非饱和渗透系数曲线分别如图3、图4所示。坡体为均质，考虑较潮湿的环境，其基质吸力设为-10kPa。

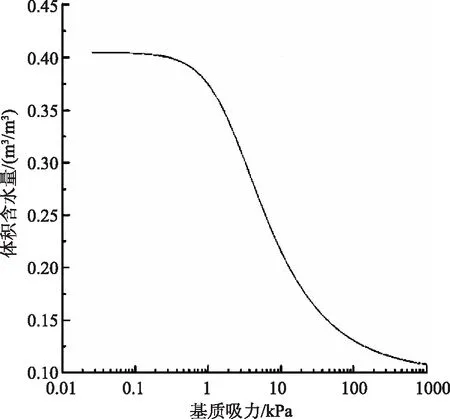
图3 粉土土水特征曲线

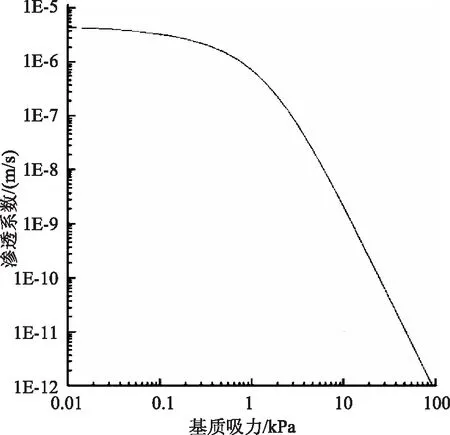
图4 粉土非饱和渗透系数

2.2 模型设计

裂隙的存在可以大大扩展饱和带的范围。因此为了解存在裂隙情况下的边坡降雨入渗和渗流过程，设计数值模型如图5所示。裂隙入渗边界根据裂隙的高度设置总水头(head)压力，如左边裂隙的最高点为(8，10.5)(单位m，下同)，则在裂隙上施加10.5m总水头边界，而右边裂隙相应施加8m总水头边界，从而保证裂隙中的水柱由上到下为静水压力状态。

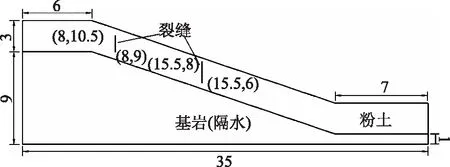
图5 边坡模型

2.3 仅考虑裂缝

(1)不存在地下水位

存在这样一种情况，短历时、高强度的降雨往往使坡表有限深度范围内的土体发生饱和，但是形成的坡表径流会汇集在坡体内的裂缝中，沿裂缝向两边渗流，模拟结果如图6所示。在不存在地下水位的情况下，饱和带沿裂缝向两边扩展，且顺坡向扩展范围较大。饱和带的扩展一方面增加了坡体的自重，另一方面也降低了底部土体的强度，这两者均会使坡体的Fs降低。

可以分别计算不同时间下坡体的Fs值，如图6(c)所示。由图可以明显看出，曲线呈曲折状，特别是5hr左右的时候Fs下降迅速，原因是由于中部裂隙的饱和带扩展到土岩界面，造成底部土体强度降低。经过24hr的渗流，坡体Fs由原来的2.795变为2.378，降低了0.417。这只是考虑裂隙渗流的情况，并未考虑降雨和由于裂隙的存在造成坡体结构的不连续。由于模型为有限元模型，故无法考虑裂隙的张开情况，同时由于软件自身功能的限制，无法在裂隙上施加静水压力的作用。以上的两个限制，造成计算得到的坡体Fs应该比实际情况要高。

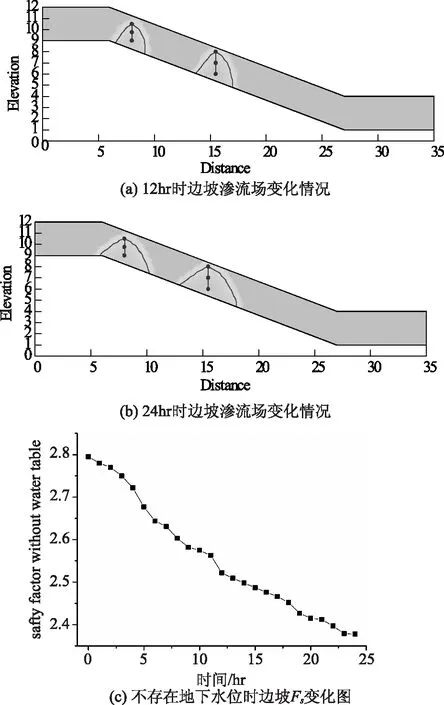
图6

(2)存在地下水位

有地下水位的情况，饱和带的扩展和不存在地下水位的情况有着明显的差别。前者饱和带边界近似一个金字塔形，两边为与地下水位线相切的下凹曲线，沿坡向扩展半径较大，主要使地下水位抬升；后者类似纺锤形的上半段，顶部平滑，两边曲线为上凸曲线，扩展半径小于前者。这也反映了两种不同边界条件下的渗流结果。地下水位的抬升将会使滑面处的孔隙水压力增大，降低了滑带的有效应力，使得坡体的抗滑力下降。存在地下水位的情况Fs随时间变化情况如图7(c)所示。

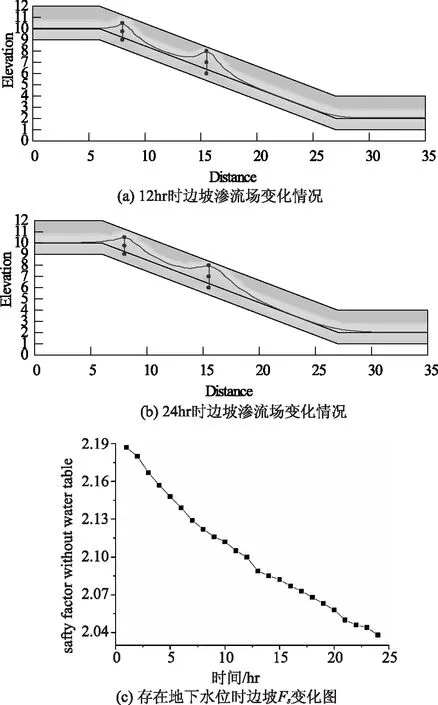
图7

2.4 降雨条件下存在裂缝的情况

如图8所示，考虑存在地下水位。12hr时，裂缝两边的地下水位显著抬升，裂隙底部土体中形成较大的孔隙水压力集中，这会使得导致土体有效应力降低，从而减弱坡体的抗滑性能。在坡体表面形成大约0.3～0.4m厚的饱和带，如图8所示(图中饱和水位线的位置与模型网格划分的大小有关，网格划分越小，水位线的位置表现的越精细)，已经与中部裂缝形成的饱和带贯通。

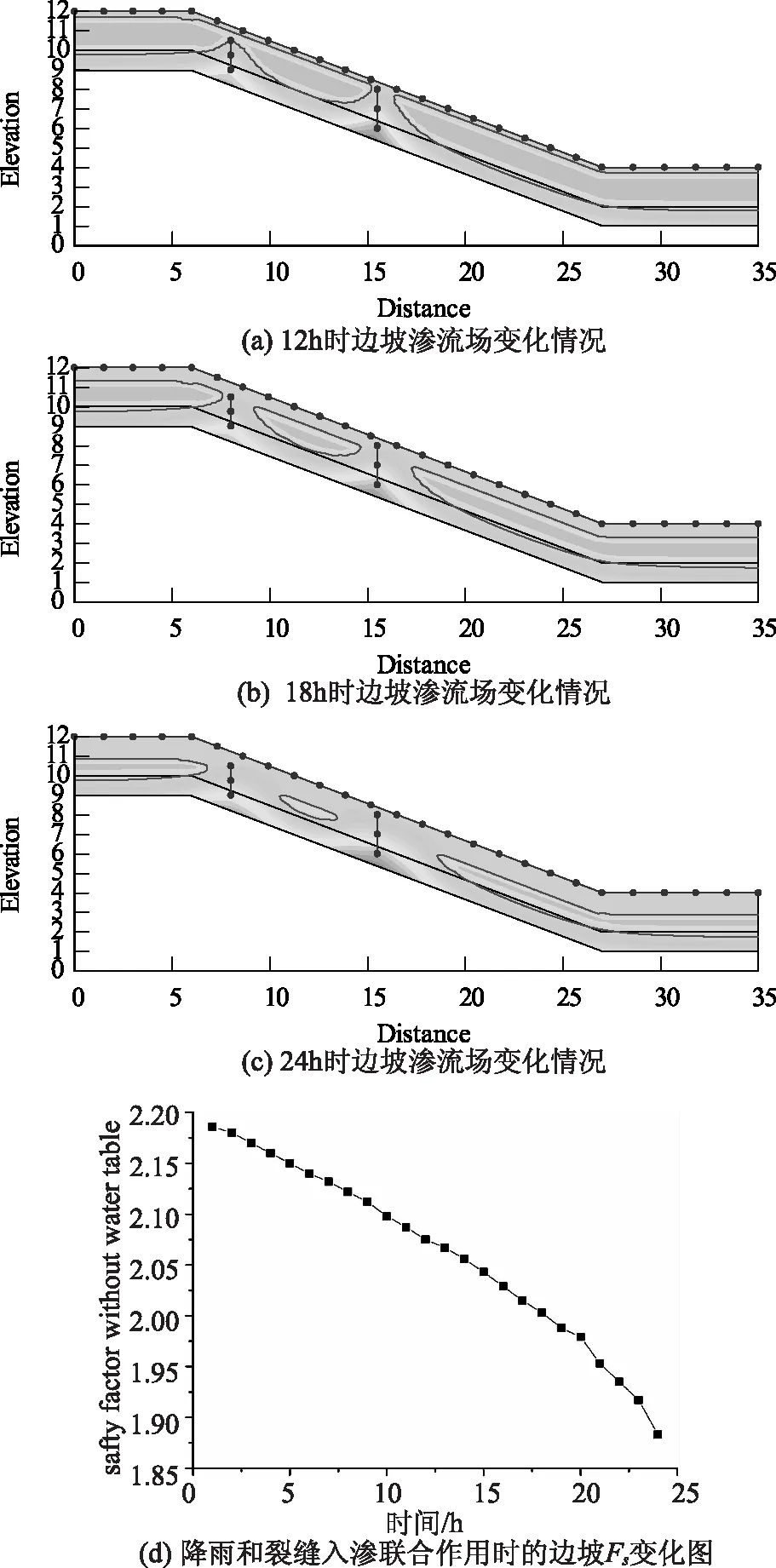
图8 降雨和裂缝条件下模拟结果图

18h时，地表饱和带已经达到约0.8m深度，与两裂缝饱和带大范围贯通，在断面上非饱和带面积逐步减小，饱和带的面积接近断面总面积的一半，坡体的重量继续增加，Fs不断下降。

降雨一天时间，在两裂缝周边形成宽广的饱和带，断面上饱和带面积已经超过三分之二，与此同时，裂缝下部的孔隙水压力集中带的面积也逐渐扩展，最大孔隙水压力继续增加。由边坡Fs图8(c)可知，在20h以后，Fs下降率有较大的增加，原因可能就是滑带底部孔隙水压力值增大，造成土体的有效应力减小。

3 结论

文章以浅层滑坡为研究对象，建立了均质等厚斜坡模型，对不同情况开展了数值模拟研究。结果表明，裂隙作为优势入渗通道，使得降雨能快速渗入到滑面位置，或者与地下水接触，提高了滑面处的有效应力，降低了边坡的稳定性。具体结论如下：

(1)随降雨时间的增长，坡体稳定性Fs逐渐降低，在相同降雨条件下，存在地下水位的情况Fs下降更低。

(2)当有裂缝存在时，入渗由表面无压入渗变为裂隙周边的有压入渗，初始压力水头的存在使得入渗饱和带的面积扩展要快于表面无压入渗，也即，裂隙入渗的影响范围要大于同等条件下表面降雨入渗的影响范围。这也就是工程中需要设置截水沟等排水设施以尽量避免坡体裂缝积水的一个原因。