考虑材料失效准则的吸能装置失效行为与碰撞特性

冯悦，肖守讷，朱涛，杨冰，阳光武，车全伟



考虑材料失效准则的吸能装置失效行为与碰撞特性

冯悦1，肖守讷1，朱涛1，杨冰1，阳光武1，车全伟2

(1. 西南交通大学 牵引动力国家重点实验室，四川 成都，610031；2. 中车青岛四方机车车辆股份有限公司，山东 青岛，266111)

在对广义增量应力状态相关损伤模型(GISSMO)失效准则5个基本特性分析的基础上，以DP800为基础材料，从应变场分布、失效单元应力三轴度和应力−应变关系3个方面验证GISSMO失效准则在仿真过程中预测各向同性韧性材料失效的准确性；在此基础上，以挤压式与压溃式2种机车车辆常用吸能装置为研究对象，对比不考虑失效、考虑V-M应变失效准则，考虑GISSMO失效准则条件下，2种吸能装置的失效行为与碰撞特性。研究结果表明：GISSMO失效准则在描述各向同性韧性材料失效行为方面具有较大的优势；吸能装置在轴向碰撞过程中的应力三轴度处于不断变化中，采用考虑应力三轴度的GISSMO失效准则使得仿真结果更准确；针对压溃式吸能装置，在材料断裂应变较小时，采用GISSMO失效准则的仿真计算中结构压溃过程会出现大面积撕裂等失效行为，降低结构的碰撞力和吸能量，在此类吸能装置设计的材料选择中应选择断裂应变较大的材料。

机车车辆；耐撞性能；吸能装置；失效准则

随着轨道交通装备的快速发展，机车车辆碰撞事故频发，机车车辆被动安全性受到越来越多的关注。在对机车车辆的碰撞研究中，有限元仿真是主要的研究方式。随着对有限元仿真精度要求的提高，人们在碰撞有限元仿真中开始更多关注材料的动态失效行为。目前在机车车辆碰撞仿真中对于材料失效行为的研究较少[1−2]，而在船舶与汽车行业对材料失效行为的研究取得了一定的进展。由于车辆及船舶结构的复杂性，目前碰撞有限元仿真中通常采用壳单元进行建模，并通过单元删除法来模拟结构的断裂失效[3−4]。因此，确定合适的失效准则以判定单元失效状态是影响此类仿真分析准确性的关键环节。失效准则从形式上可分为2种：一种是基于连续介质损伤力学从微观空穴发展而提出的失效准则，另一种是基于断裂应变的半经验性的失效准则。由于第1种失效准则采用的是积分形式，其临界损伤值难以测定，因此在通用的商业软件中并没有得到广泛应用；第2种失效准则由于其表达形式简单且失效参数可通过试验较为方便地测定，因而被广泛地嵌入到通用商业软件，应用于碰撞仿真。目前应用在碰撞仿真中的失效准则主要有等效(V-M)应变失效准则、最大主应变失效准则、厚度方向应变失效准则、Johnson-Cook(J-C)失效准则等。赵效东[4]通过简单的梁受载弯曲破坏模拟对比了在V-M应变失效准则、最大主应变失效准则、厚度方向应变失效准则下的仿真结果，阐述了3种失效准则在碰撞仿真中的缺陷，并提出厚度应变与主应变组合判断结构失效的新型失效准则，通过与试验结果对比证明了厚度应变与主应变组合的新型失效准则的可行性。刘敬喜等[5]基于3种典型舷侧结构缩尺模型的准静态耐撞性试验，采用V-M应变失效准则、主应变−厚度应变失效准则以及RTCL(Rice-Tracey & Cockcroft-Latham)失效准则对模型试验进行数值模拟，研究结果表明：引入应力三轴度的RTCL准则能更准确地模拟不同结构的裂纹产生过程。张志强等[6]针对典型的船体双层壳结构，重点研究极限塑性准则(GL)，RTCL和J-C这3种常用失效准则在碰撞破坏仿真分析中的应用，发现板壳结构在碰撞载荷下，撞击中心的应力三轴度为0.3~0.6，考虑应力三轴度的RTCL和J-C失效准则更能真实反应板的撞击破坏。虽然RTCL和J-C失效准则考虑了应力状态，但其有一定的局限性，即在整个应力三轴度范围内断裂应变都为单调函数，而对于14MnNbq 等金属材料，其断裂应变与应力三轴度并非单调关系，故其使用范围还有待进一步研究[7]。针对上述失效准则的局限性以及碰撞仿真中多采用的各向同性材料模型，NEUKAMM等[8−14]开发并完善了嵌于LS-DYNA中的广义增量应力状态相关损伤模型(GISSMO)。ANDRADE等[15]将该准则应用于描述双相钢材料的失效行为，其结果表明：GISSMO失效准则能够重现多个载荷路径下各向同性韧性材料的断裂行为｡HÖRLING[16−17]分别获得了DOCOL 1200M和DOCOL 900M这2种材料的GISSMO失效准则的参数，其结果表明GISSMO失效准则能很好地预测上述2种材料的失效行为的能力。而随着GISSMO失效准则的推广应用，国内研究者也开始将该准则应用于碰撞仿真。庄华晔等[18−19]最早在汽车领域的碰撞仿真中使用了该失效准则，试验与仿真对比结果表明GISSMO失效准则能够很好地预测各向同性韧性材料失效行为。因此，本文作者对GISSMO失效准则进行深入研究，并与V-M应变失效准则进行对比，研究其对列车常用薄壁管吸能装置碰撞性能的影响。

1 GISSMO失效准则

GISSMO失效准则应力状态相关的增量损伤准则，具有如下5个基本特性。

1) 损伤演变。该特性主要通过损伤累积的方法解决非线性应变路径加载的问题。损伤计算公式如下：

式中：m为平均应力；eq为等效应力；1，2和3分别为第1，第2和第3主应力。

损伤累积的概念在J-C失效准则中也有体现，但其中的损伤累积指数=1，累积为线性累积，而实际变形过程中的累积为非线性的，即当塑性应变接近断裂应变(即接近1)时，同样的塑性应变增量引起的损伤增量会更大，即损伤会加速。显然，GISSMO失效准则中的非线性累积过程与实际结果更相符。

2) 临界塑性应变与应力/损伤耦合。该特性主要用于描述损伤累积与应力减弱之间的耦合关系，即在塑性应变达到临界应变之后，流动应力会因为损伤累积而逐渐减小。决定材料是否发生应力减弱的变量为稳定性变量，其与损伤变量具有相近的累积形式。

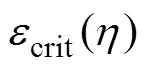
依据式(3)非线性累积，当增大至1时，应力开始减弱，减弱后的应力计算公式为

随着塑性应变增大，稳定性变量逐渐增大，当增大为1时，应力与损伤的耦合关系开始发生；随着损伤变量进一步增大，应力开始减小，当增大为1时，应力减弱为0 MPa。GISSMO准则的此种特性是其他失效准则不具备的特性，使得计算得到的材料应力与真实试验结果更加相符。

3) 网格单元尺寸效应修正。此种特性主要用于修正由应变局部化引起的不同单元尺寸对断裂预测的影响。准则中提出了对断裂应变的修正函数，修正后损伤变量的计算公式如下：

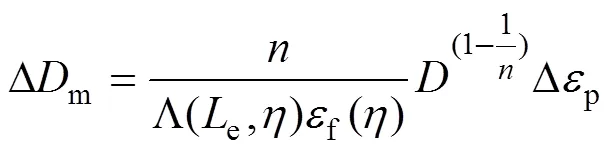
4) 模拟壳单元的弯曲。壳单元在弯曲状态时，一侧承受拉伸载荷，另一侧承受压缩载荷。对于金属材料而言，受拉伸载荷比压缩载荷更容易失效。为了更准确地模拟金属材料的此种特性，准则将对失效的判断施加于单元厚度方向上的每个积分点上。例如，如果单元在厚度方向设置有5个积分点，那么在弯曲工况下，受拉侧的积分点先于受压侧的积分点失效，直到单元所包含的5个积分点均达到失效极限，单元才会被删除。相比于某些方法中只针对壳单元的中间层进行失效评定，此种方法使得单元失效与实际更加 接近。

5) 数值实现。该准则嵌入在LS-DYNA程序中，能通过“MAT_ADD_EROSION”调用。另外与J-C失效准则不同，该准则可以与任何材料弹塑性模型耦合使用，极大地提高了失效准则应用的灵活性。

2 材料参数及验证

DP800属于应变率敏感材料，具有明显的应变率强化效应，其在不同应变率下的塑性应变−流动应力曲线如图1所示[20]。

应变率/s−1：1—2 250；2—1 000；3—500；4—0.01；5—0.001。

对于DP800材料的GISSMO失效参数，ANDRADE等[15]通过不同应力状态下的准静态试验，得出了等效断裂塑性应变、临界塑性应变与应力三轴度的关系，如图2所示。其中失效参数=2，=2.5，且材料应变率对失效参数的影响可忽略不计。ANDRADE等[15]采用已得到的失效参数对汽车的B柱结构进行了碰撞仿真，其结果表明采用了GISSMO失效准则的仿真实验中预测的变形及整体弯曲形式与试验测试结果高度吻合，准确地反映了结构在碰撞中的失效行为，验证了该准则及其参数对于DP800材料失效行为描述的准确性。

1—断裂塑性应变；2—临界塑性应变。

图2 断裂塑性应变及临界塑性应变与应力三轴度的关系[15]

Fig. 2 Relationship between fracture plastic strain, critical plastic strain and stress triaxiality[15]

对于V-M应变失效准则，即等效塑性应变失效准则，因其具有简便性而在碰撞仿真领域得到了广泛应用。等效塑性应变的计算公式为

式中：eff为等效塑性应变；1，2和3分别为第1，第2和第3主应变。

该准则没有考虑不同应力状态对断裂应变的影响，即当单元的等效塑性应变达到等效断裂塑性应变时，单元即从计算中消失。根据其定义，本文将单轴拉伸的等效塑性断裂应变定义为V-M应变失效的阈值，根据试验结果可知V-M等效断裂塑性应变为1。

由于需要采用有限元仿真对不同失效准则的影响开展研究，为确保仿真方法的准确性，分别依据材料的GISSMO失效准则与V-M应变失效准则对简单试样进行仿真，GISSMO准则按文献[15]进行参数设置，V-M断裂应变设置为1，单元类型设置为全积分线性壳单元，厚度方向设置5个积分点，单元边长为0.5 mm。

将断裂前一时刻试样应变场分布的仿真结果与试验结果[15]对比，如图3所示。由图3可以看出：在拉伸、缺口拉伸、0°剪切与45°剪切的应力状态下，通过GISSMO仿真得到的应变场分布与试验结果基本吻合。

(a) 试验结果，拉伸状态[15]；(b) 试验结果，缺口拉伸状态[15]；(c) 试验结果，0°剪切状态[15]； (d) 试验结果，45°剪切状态[15]；(e) GISSMO失效准则，拉伸状态；(f) GISSMO失效准则，缺口拉伸状态； (g) GISSMO失效准则，0°剪切状态；(h) GISSMO失效准则，45°剪切状态；(i) V-M失效准则，拉伸状态； (j) V-M失效准则，缺口拉伸状态；(k) V-M失效准则，0°剪切状态；(l) V-M失效准则，45°剪切状态

采用V-M应变失效准则的仿真结果，除单轴拉伸与0°剪切的应力状态外，其他应力状态下的仿真结果均与试验结果存在较大差异。对于缺口拉伸与45°剪切，在V-M应变失效准则下，断裂前单元的塑性应变明显大于真实应变，实际材料在较小应变时就已经失效。

V-M与GISSMO失效准则下材料的应力−应变关系如图5所示。由图5可知：即使对于单轴拉伸试验，由于GISSMO准则考虑了损伤与应力的耦合，材料的应力−应变曲线展现出颈缩之后的应力减弱现象。

综上所述，本文在材料多应力状态拉伸试验的有限元模型中对于GISSMO失效模型参数的设置是准确的，可以在结构碰撞仿真中采取同样的设置方法。另外，由GISSMO失效准则与V-M应变失效准则的仿真结果进行对比可知：GISSMO失效准则在表现材料失效行为方面比V-M应变失效准则更准确。

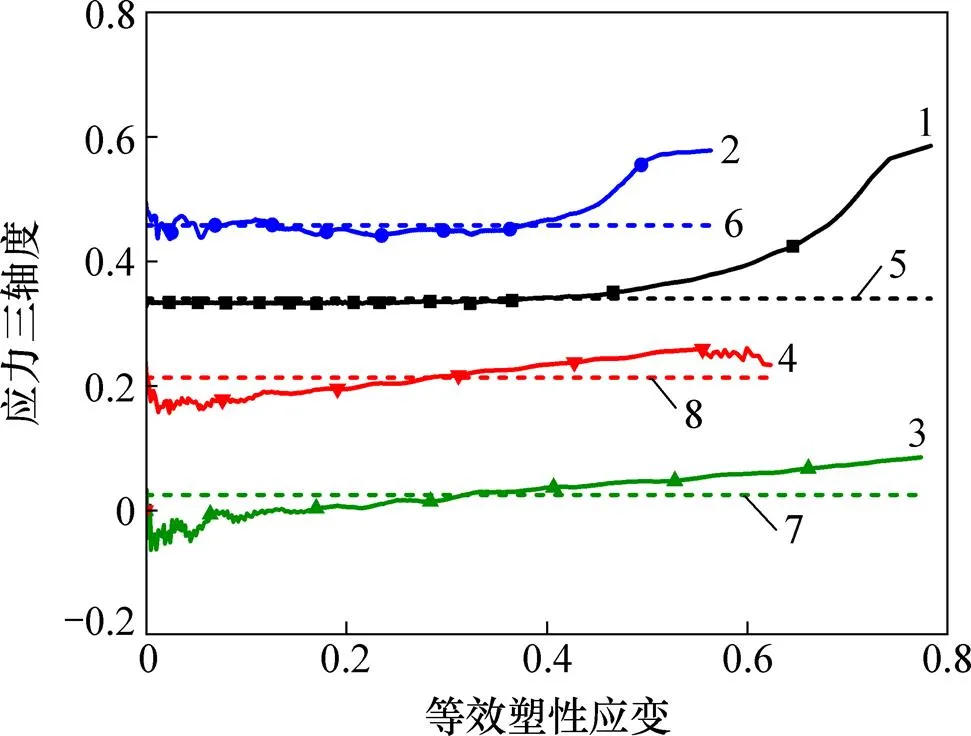
1—拉伸；2—缺口拉伸；3—0°剪切；4—45°剪切； 5—=0.340；6—=0.458； 7—=0.025；8—=0.213。

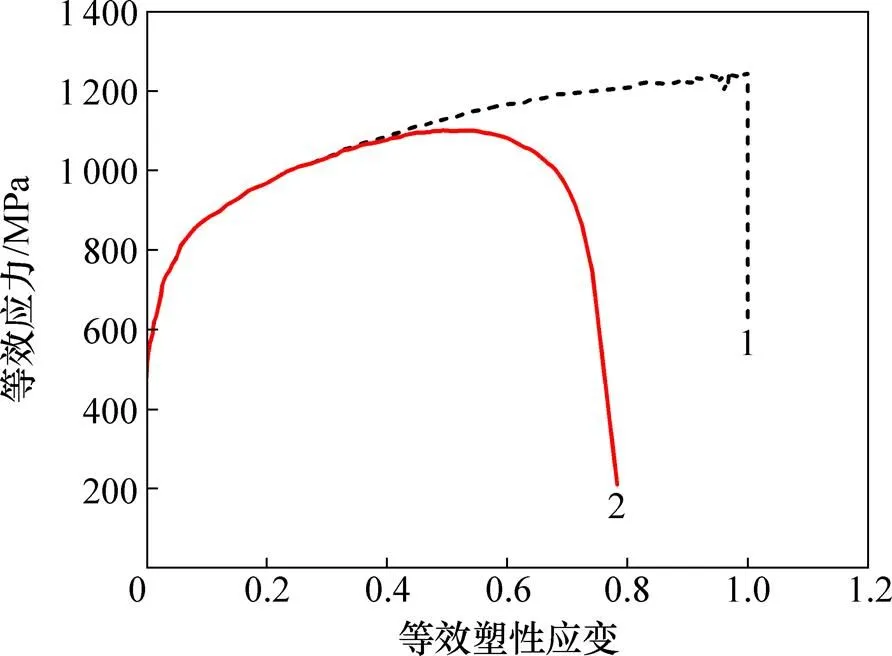
1—V-M；2—GISSMO。

3 吸能装置碰撞仿真

针对列车常用的薄壁挤压式吸能装置与压溃式吸能装置，分别采用不考虑失效，考虑V-M应变失效准则，考虑GISSMO失效准则开展碰撞仿真研究，探究不同类型吸能装置仿真结果受失效准则的影响，以期指导结构设计中对材料性能的需求。

挤压式吸能装置为薄壁圆管，圆管半径为75 mm；压溃式吸能装置为简单薄壁管结构，截面形状分别为圆形、正方形与正六边形，内切圆的半径为75 mm，轴向高度均为400 mm。4组吸能装置的吸能管壁厚均为4 mm，单元边长为2 mm，吸能装置结构示意图如图6所示。

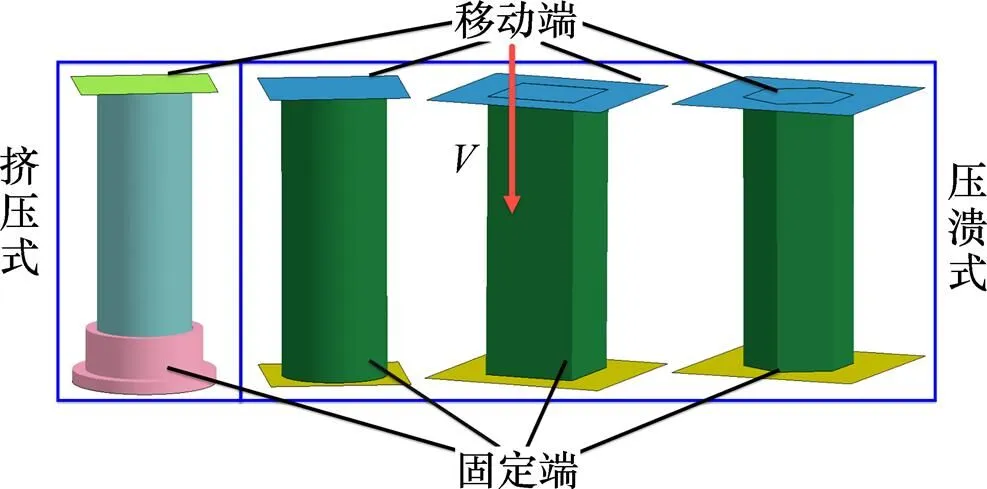
图6 吸能装置结构示意图

图7 GISSMO准则单元边长修正曲线

3.1 碰撞过程中应力三轴度的变化

对于挤压式吸能装置，在不考虑失效时，薄壁圆管挤压完成后的应力三轴度是均匀分布的。挤压式吸能装置应力三轴度分布云图如图8所示。由图8可知：在受到挤压之后应力三轴度均为0.667左右，大于单轴拉伸时的应力三轴度0.333。

对于压溃式吸能装置，在不考虑失效时，不同截面薄壁管压溃过程中的应力三轴度分布如图9所示。由图9可知：在轴向压溃过程中，不同位置处的应力三轴度不同，且处于不断变化的状态。根据应力三轴度的计算公式，对于平面壳单元，应力三轴度范围为−0.667~+0.667。在压溃过程中，褶皱形成的塑性铰附近均会出现应力三轴度的峰值。而对于试验中的单轴拉伸试样，其应力三轴度基本在0.333附近波动。材料在不同应力三轴度下的断裂应变差异较大，如果仅以此种拉伸情况下的断裂特性代表材料在全应力状态下的断裂特性并用于吸能装置仿真必然使仿真结果出现较大差异。

综上可知，对于上述2类吸能装置，在受载过程中的应力三轴度均不是保持0.333不变，以材料在单轴拉伸状态下的断裂应变作为结构变形中的恒定断裂应变是不合理的，因此，有必要对材料的断裂应变受应力三轴度的影响进行研究，同时在结构碰撞仿真中应优先采用考虑应力三轴度的失效准则。

3.2 变形模式

挤压式吸能装置应变分布云图如图10所示。由图10可知：在整个变形过程中，其等效塑性应变的最大值小于0.27，距离材料在对应应力三轴度下的断裂应变还有一定的差距，整个变形过程中均没有出现结构的断裂，故不考虑失效与失效准则的选取均未对结构的变形模式产生影响。

对于压溃式吸能装置，由于变形过程中形成了塑性铰，塑性应变较大，不同失效准则下的变形模式出现明显差异。以截面为正方形的薄壁结构为例进行分析，不同失效准则下结构变形模式如图11所示。

对于未考虑失效的模型NONE，单元可以无限制变形，虽然结构棱边附近单元的塑性应变已经超过1.0，但仍然没有出现单元失效现象。

对于V-M应变失效准则，在结构4条棱边附近的塑性铰处的塑性应变达到同期应变场分布的最大值，由于断裂应变设置为1.0，当局部单元塑性应变达到断裂应变1.0时，单元消失，即裂纹产生。但由于设置的失效标准较高，断裂仅出现在局部边角，结构的整体的塑性铰形成的变形模式未发生明显改变。从宏观变形来看，采用V-M应变失效准则与未考虑失效的变形模式差异较小。

图8 挤压式吸能装置应力三轴度分布云图

(a) 圆形管，15 ms；(b) 圆形管，30 ms；(c) 圆形管，45 ms；(d) 圆形管，60 ms； (e) 正方形管，15 ms；(f) 正方形管，30 ms；(g) 正方形管，45 ms；(h) 正方形管，60 ms； (i) 正六边形管，15 ms；(j) 正六边形管，30 ms；(k) 正六边形管，45 ms；(l)正六边形管，60 ms

图10 挤压式吸能装置应变分布云图

对于GISSMO失效准则，结构发生了大面积的撕裂。结构在变形过程中的应力三轴度较大，而对于DP800材料，应力三轴度超过0.333后再继续增大，将导致断裂应变减少，显然结构变形过程中单元塑性应变更容易超过失效标准，故断裂会大面积发生。断裂出现的初始位置如图12(a)所示。虽然此时单元的最大塑性应变在0.52以内，但前一步计算的应力三轴度基本在0.45以上，应力状态分布如图12(b)所示。根据失效准则，最大塑性应变已经超过了准则中对应应力三轴度下的断裂应变，故断裂的初始位置是准确的。伴随着压溃的持续进行，初始萌生的裂缝会持续扩展，在塑性铰位置完全断裂，并在棱边出现持续的撕裂现象。

由于仿真中使用GISSMO失效准则使得结构失效比较严重，为确保仿真中失效行为是由材料性质引起的而不是仿真的失误，参考汽车用某种金属板材的参数[18]，设置GISSMO准则中材料的断裂应变，同时取消应力和损伤的耦合，断裂应变与应力三轴度关系如图13所示。根据失效准则的算法，此处应力和损伤的耦合设置仅影响失效后的应力是否减弱，不会影响失效行为的出现。新的断裂应变下结构变形模式仿真结果如图14所示。由图14可知：在断裂应变增加之后，结构的失效行为明显减少，说明仿真结果的差异的确是由材料本身的性质引起的。对于DP800这种断裂应变较小的材料在结构压溃过程中会产生比较严重的撕裂行为。

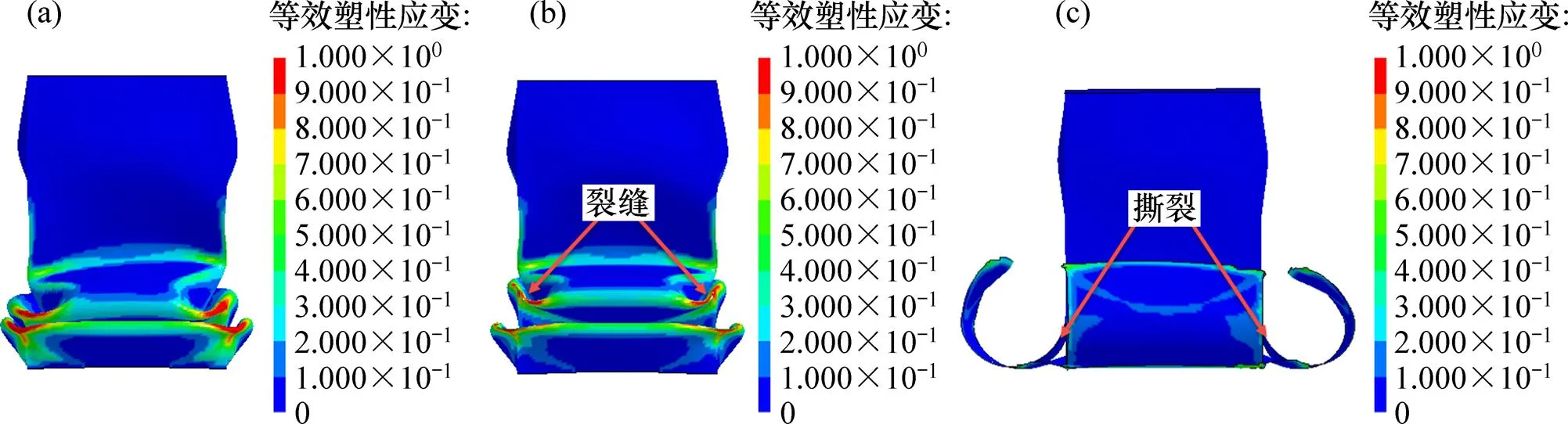
(a) 不考虑失效；(b) V-M失效准则；(c) GISSMO失效准则

(a) 初始断裂位置；(b) 应力状态分布

综上所述，失效准则的选取对变形较大的压溃式吸能装置碰撞仿真中的变形模式影响显著。在材料具备与DP800相似的断裂特性时，与未考虑失效的仿真及V-M应变失效准则下的仿真相比，GISSMO失效准则下结构发生了更大面积的断裂行为，整体变形由塑性铰形成变为撕裂，差异显著。

图13 断裂应变与应力三轴度关系[18]

图14 新的断裂应变下结构变形模式仿真结果

3.3 压溃力与能量吸收

对于挤压式吸能装置，由于变形中的塑性应变较小，未达到材料的临界失稳应变，故未出现损伤与应力耦合导致的单元应力减弱。同时由于失效准则的选取对其变形模式未产生明显影响，故未考虑失效与失效准则的选取没有对结构的碰撞力与能量吸收产生明显影响。

对于压溃式吸能装置，不同失效准则下结构压溃力和能量吸收曲线如图15所示。从图15(a)可以看出：在初始时刻，由于塑性应变较小，断裂尚未发生，3个模型产生的初始峰值力基本重合。随着变形的继续，变形模式的明显差异引起压溃力的不同。在V-M应变失效准则下，局部断裂未影响整体变形模式，变形比较充分，压溃力没有发生明显的变化。但对于GISSMO失效准则，结构的撕裂行为代替了原有的塑性铰的形成。变形过程中的碰撞力来源变为结构棱边的持续撕裂。撕裂过程中的撕裂力比塑性铰依次形成的压溃力更加平稳，但数值更小，故导致了压溃力在峰值之后的急剧下降，并维持在较低水平。对于GISSMO失效准则，由于考虑了损伤累积与应力减弱的耦合，临界失稳应变之后的应力减弱也在一定程度上减弱了碰撞过程中的压溃力。上述2个因素导致了结构能量吸收减少，最终的能量吸收水平仅为原始的20%。

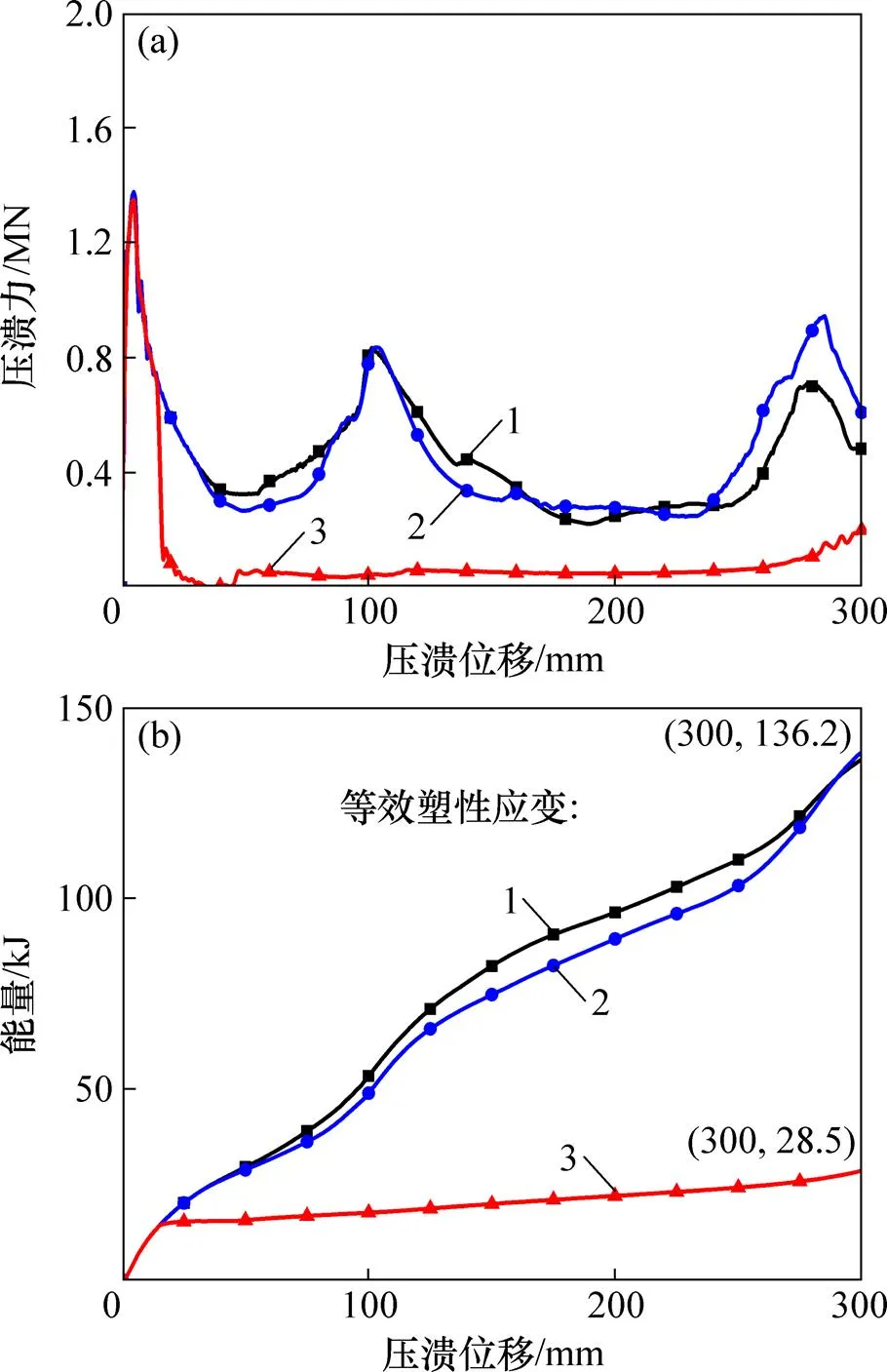
(a) 压溃力−位移曲线；(b) 能量吸收−位移曲线

综上可知：不同失效准则对变形较大的压溃式吸能装置碰撞仿真中的压溃力与能量吸收等碰撞特性影响显著。当材料具备与DP800相似的断裂特性时，与未考虑失效的仿真结果及V-M应变失效准则下的仿真结果相比，采用GISSMO失效准则的仿真中结构发生了更大面积的断裂行为，整体变形由塑性铰形成变为撕裂，结构的压溃力与能量吸收比未考虑失效及V-M应变失效准则下的更小，即对于使用DP800材料的压溃式吸能装置，实际的压溃试验得到的压溃力与能量吸收将明显小于不考虑失效及V-M应变失效准则下的仿真计算值。因此，在进行吸能装置设计中应避免采用具有类似断裂特性的材料，尽量选择断裂应变较大的材料，以保证吸能装置的吸能性能。

4 结论

1) 对于各向同性韧性材料的失效行为，GISSMO失效准则考虑了应力状态、损伤累积、网格尺寸效应以及壳单元弯曲等方面，比V-M应变失效准则考虑更全面，在模拟各向同性韧性材料失效行为方面具有突出的优势，对于此类材料失效行为的研究，建议采用此种失效准则。

2) 不同类型的吸能装置在受载过程中，应力三轴度处于不断的变化之中，仅用单一恒定断裂应变判断材料的失效是远远不够的，应研究材料失效行为受应力状态的影响，并在结构仿真中优先采用考虑了应力三轴度的失效准则。

3) 对于挤压式吸能装置的碰撞仿真，由于变形过程中塑性应变较小，变形模式、压溃力及吸能量基本不受失效准则影响；对于变形较大的压溃式吸能装置的碰撞仿真，基于DP800的材料失效特性，与未考虑失效及V-M应变失效准则下的仿真结果相比，使用GISSMO失效准则的仿真中结构会出现塑性铰的断裂与沿结构的棱边的撕裂等失效行为，结构的压溃力与能量吸收减少，该仿真结果与实际结果更接近，不同失效准则对该种吸能装置的碰撞仿真结果影响显著，结构碰撞仿真中应该优先采用GISSMO失效准则。

4) 对于使用DP800材料的压溃式吸能装置，由于该材料断裂应变较小，实际的压溃试验得到的压溃力与能量吸收将明显小于不考虑失效及V-M应变失效准则下的仿真结果，在结构设计的材料选择中，应该尽量选用断裂应变较大的材料以保证吸能装置的吸能特性。

[1] 朱涛, 肖守讷, 杨超, 等. 机车车辆被动安全性研究综述[J]. 铁道学报, 2017, 39(5): 22−32. ZHU Tao, XIAO Shoune, YANG Chao, et al. State-of-the-art development of passive safety of rolling stocks[J]. Journal of the China Railway Society, 2017, 39(5): 22−32.

[2] 雷成, 肖守讷, 罗世辉, 等. 轨道车辆耐碰撞性研究进展[J]. 铁道学报, 2013, 35(1): 31−40. LEI Cheng, XIAO Shoune, LUO Shihui, et al. State-of-the-art research development of rail vehicles crashworthiness[J]. Journal of the China Railway Society, 2013, 35(1): 31−40.

[3] 赵华, 吴英龙, 王萌. 汽车碰撞仿真研究进展[J]. 哈尔滨理工大学学报, 2012, 17(4): 27−33. ZHAO Hua, WU Yinglong, WANG Meng. The status quo of FEM simulation on vehicle collision[J]. Journal of Harbin University of Science and Technology, 2012, 17(4): 27−33.

[4] 赵效东. 海洋工程结构物碰撞失效准则研究[D]. 哈尔滨: 哈尔滨工程大学船舶工程学院, 2010: 27−69. ZHAO Xiaodong. Research of failure criterion of offshore structural collision[D]. Harbin: Harbin Engineering University. School of Naval Architecture, 2010: 27−69.

[5] 刘敬喜, 崔濛, 龚榆峰. 船舶碰撞仿真失效准则比较[J]. 中国舰船研究, 2015, 10(4): 79−85. LIU Jingxi, CUI Meng, GONG Yufeng. A comparative study of failure criteria in ship collision simulations[J]. Chinese Journal of Ship Research, 2015, 10(4): 79−85.

[6] 张志强, 李华峰, 张咏鸥, 等. 失效准则在船舶碰撞破坏中的应用研究[J]. 舰船科学技术, 2017, 39(1): 56−62. ZHANG Zhiqiang, LI Huafeng, ZHANG Yongou, et al. An application research on failure criteria of collision damage in ship structures[J]. Ship Science and Technology, 2017, 39(1): 56−62.

[7] 陈继恩. 基于应力三轴度的材料失效研究[D]. 武汉: 华中科技大学船舶与海洋工程学院, 2012: 62−63. CHEN Jien. Research of material failure basic on stress triaxiality[D]. Wuhan: Huazhong University of Science and Technology. School of Naval Architecture and Ocean Engineering, 2012: 62−63.

[8] NEUKAMM F, FEUCHT M, ROLL K, et al. On closing the constitutive gap between forming and crash simulation[C]// Proceedings of the 10th International LS-DYNA Users Conference. Detroit, USA: Livermore Software Technology Corp, 2008: 21−31.

[9] NEUKAMM F, FEUCHT M, HAUFE A. Considering damage history in crashworthiness simulations[C]//Proceedings of the 7th European LS-DYNA Users Conference. Salzburg, Austria: DYNAmore GmbH, 2009: 1−9.

[10] HAUFE A, FEUCHT M, NEUKAMM F. The challenge to predict material failure in crashworthiness applications: simulation of producibility to serviceability[C]//Predictive Modeling of Dynamic Processes. Boston, USA: Springer, 2009: 67−88.

[11] FEUCHT M, NEUKAMM F, HAUFE A. A phenomenological damage model to predict material failure in crashworthiness applications[C]//Recent Developments and Innovative Applications in Computational Mechanics. Berlin, Germany: Springer, 2011: 143−153.

[12] EFFELSBERG J, HAUFE A, FEUCHT M, et al. On parameter identification for the GISSMO damage model[C]//Proceedings of the 12th International LS-DYNA Users Conference. Detroit, USA, 2012: 1−10.

[13] HAUFE A, ANDRADE F, FEUCHT M, et al. The forming-to-crash simulation process chain: new challenges and efficient modeling techniques[C]//Proceedings of the International Conference of New Developments in Sheet Metal Forming. Fellbach, Germany, 2014: 1−5.

[14] ANDRADE F, FEUCHT M, HAUFE A. On the prediction of material failure in LS-DYNA: a comparison between GISSMO and DIEM[C]//Proceedings of the 13th International LS-DYNA Users Conference. Detroit, USA, 2014: 1−10.

[15] ANDRADE F X C, FEUCHT M, HAUFE A, et al. An incremental stress state dependent damage model for ductile failure prediction[J]. International Journal of Fracture, 2016, 200(1/2): 1−24.

[16] HÖRLING D. Parameter identification of GISSMO damage model for DOCOL 1200M : A study on crash simulation for high strength steel sheet components[D]. Karlstad, Sweden: Karlstad University. Faculty of Health, Science and Technology, 2015: 1−33.

[17] CHALAVADI S K. Parameter identification of GISSMO damage model for DOCOL 900M high strength steel alloy: Usage of a general damage model coupled with material modeling in LS-DYNA for Advanced high strength steel crashworthiness simulations[D]. Trolatan, Sweden: University West. Department of Engineering Science, 2017: 1−12.

[18] 庄华晔, 田雨苗, 赖兴华. 金属板材不同应力状态断裂试验及断裂模型建立[J]. 汽车工艺与材料, 2016(11): 43−47. ZHUANG Huaye, TIAN Yumiao, LAI Xinghua. Fracture test and fracture model establishment of sheet metal under different stress states[J]. Automobile Technology and Material, 2016(11): 43−47.

[19] 赖兴华, 王磊, 李洁, 等. 铝型材防撞梁的碰撞断裂失效表征[J]. 清华大学学报(自然科学版), 2017, 57(5): 504−510. LAI Xinghua, WANG Lei, LI Jie, et al. Characterization of the fracture of an aluminum alloy anticollision-beam to impact loading[J].Journal of Tsinghua University(Science and Technology), 2017, 57(5): 504−510.

[20] 蔡恒君, 胡靖帆, 宋仁伯, 等.800MPa级冷轧双相钢的动态变形行为及本构模型[J].工程科学学报, 2016, 38(2): 213−222. CAI Hengjun, HU Jingfan, SONG Renbo, et al. Constitutive model and dynamic deformation behavior of 800 MPa grade cold-rolled dual phase steel[J]. Chinese Journal of Engineering, 2016, 38(2): 213−222.

Failure behavior and collision characteristics of energy-absorbing structures considering material failure criteria

FENG Yue1, XIAO Shoune1, ZHU Tao1, YANG Bing1, YANG Guangwu1, CHE Quanwei2

(1. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China; 2. CRRC Qingdao Sifang Co. Ltd., Qingdao 266111, China)

By analyzing the five basic characteristics of the failure criterion of general incremental stress state dependent damage model (GISSMO), DP800 was selected as the basic material, and the accuracy of GISSMO for predicting isotropic ductile material failure behavior during simulation application was verified through three aspects, including strain distribution, the stress triaxiality of failure element and the relationship between stress and strain. Furthermore, the failure behavior and collision characteristics of squeezing and crushing energy-absorbing structures commonly used in the rolling stocks were simulated and compared in conditions of no failure criteria, V-M strain failure criterion and GISSMO failure criterion. The results show that the GISSMO failure criterion has great advantages in describing the failure behavior of isotropic ductile materials. The stress triaxiality of the energy-absorbing structure is constantly changing in the process of axial collision, and the simulation with GISSMO failure criterion, which takes the stress triaxiality into consideration, produces more accurate results. For crushing energy-absorbing structure, when the fracture strain of the material is small, adopting GISSMO failure criterion will cause a large-area failure behavior of the structure and reduction of the collision force and energy absorption. In the design of energy-absorbing structure, a material with a larger fracture strain should be selected.

rolling stocks; crashworthiness; energy-absorbing structure; failure criterion

10.11817/j.issn.1672−7207.2019.02.031

O313.4；U270.2

A

1672−7207(2019)02−0487−10

2018−03−12；

2018−05−11

国家自然科学基金资助项目(U1534209)；国家重点研发计划项目(2016YFB1200404)；牵引动力国家重点实验室自主课题(2017TPL_Z1, 2015TPL_T013)(Project(U1534209) supported by the National Natural Science Foundation of China; Project (2016YFB1200404) supported by the National Key Research and Development Program of China; Projects(2017TPL_Z1, 2015TPL_T013) supported by Independent Research Program of State Key Laboratory of Traction Power)

朱涛，博士，副研究员，从事机车车辆设计与理论研究；E-mail：zhutao034@swjtu.cn

(编辑 伍锦花)