土质边坡降雨入渗深度及饱和区变化规律

刘杰，曾铃，付宏渊, ，史振宁，张永杰



土质边坡降雨入渗深度及饱和区变化规律

刘杰1, 2，曾铃3，付宏渊2, 3，史振宁2，张永杰3

(1. 长沙理工大学 道路灾变防治及交通安全教育部工程研究中心，湖南 长沙，410114； 2. 长沙理工大学 交通运输工程学院，湖南 长沙，410114； 3. 长沙理工大学 土木工程学院，湖南 长沙，410114)

采用饱和−非饱和渗流有限元计算理论，建立一维、二维模型，对不同降雨强度、土质类型、表面吸力以及边坡坡度下的边坡降雨入渗深度和饱和区变化规律进行研究。研究结果表明：对于同种土质而言，初始表面吸力越小，降雨入渗深度越大，降雨入渗深度从大至小对应的土质依次为粉土、砂土和黏土；在降雨过程中，黏土在降雨入渗深度范围内均为饱和区域，而粉土则先在入渗深度范围内出现饱和区，随后饱和区域消散，砂土首先在降雨入渗范围内形成饱和区，随后饱和区下移形成悬挂式饱和区；边坡坡度越大，边坡底部的降雨入渗深度越大，粉土边坡受坡度影响更明显；在降雨作用下，当初始表面吸力为100 kPa时，砂土边坡表面生成饱和区，随后饱和区扩大并下移；而当初始表面吸力为10 kPa时，降雨会导致粉土边坡地下水位上升。

土质边坡；降雨入渗；入渗深度；饱和区

众所周知，边坡稳定性状态与当地的地质活动、天气状况以及工程建设的扰动均密切相关。在以上因素中，减小边坡受强降雨影响所产生的失稳风险是边坡工程中亟需解决的问题之一，而降雨状态下的边坡稳定性则主要由内部渗流状态决定[1−2]。在自然状态下，边坡土体绝大多数呈非饱和状态，且非饱和状态下土体的渗流特征与土体的自身性质、降雨强度以及边坡形态等多种因素有着紧密联系[3−4]。众多学者从多种角度对此进行了研究，如刘晓等[5]对存在夹砂层的边坡采用Green−Ampt模型对积水下渗过程进行分析，发现当砂层的饱和导水率相当大时，能够有效阻止水向夹砂层下层入渗；DORIVAL[6]采用非饱和理论与有限元方法对二维、三维状态下的渗流过程进行了模拟，所得结果与实际结果基本相符。可以认为非饱和渗流理论适用于计算边坡渗流特征。我国DL/T 5353—2006“水电水利工程边坡设计规范”认为在考虑降雨入渗时，降雨直接导致地下水位抬升。王智磊 等[7]也认为虽然地下水位变化对降雨的响应存在滞后效应，但最终仍会随降雨持续而上升。但BANDARA等[8−9]认为，在某些条件下，边坡降雨入渗不一定直接引起地下水位抬升，而会在边坡表面形成一定深度的饱和区，其变化规律受降雨强度和土质特征所控制。付宏渊等[10−11]的研究结果表明软岩以及粗粒土等边坡在降雨条件下会在表面形成饱和区，随着降雨持续，饱和区从坡脚处与地下水位线相接，最后导致边坡内部水位线抬升。针对这2种不同的观点，本文作者基于非饱和土渗流计算原理，采用一维、二维渗流模型进行数值计算，对降雨在何种状态下会导致地下水位上升、何时产生饱和区等进行研究，以便为浅层、深层滑坡产生机理的研究及对边坡排水等设计提供参考。

1 数值计算理论

采用二维有限元渗流理论进行计算。非饱和非稳定渗流的二维控制方程为[12]

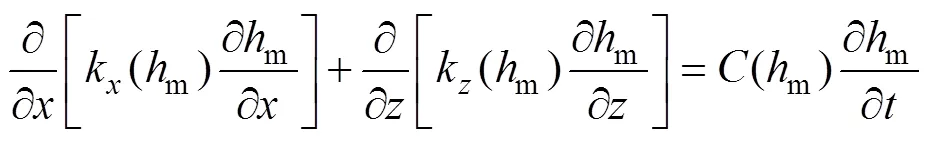
式中：和分别代表水平、竖直方向；m为基质吸力水头；(m)为非饱和土渗透系数函数；(m)为比水容量，即土水特征曲线的斜率；为时间。土体非恒定渗流有限元方程可用下式描述[13]：

式中：[]为单元特征矩阵；{}为节点水头向量；[]为单元质量矩阵；[]为节点流量向量。

2 计算参数与方案

为得到不同土质对渗流特征的影响，选取较典型的长沙湘江沿岸砂土、浙西衢州地区粉土以及湖南南部红黏土进行分析，如图1所示。通过大量室内试验测试得到这3种不同土质的孔隙比与饱和渗透系数，如表1所示。

在降雨强度取值方面，为体现极端降雨对边坡渗流特征的影响，设定降雨强度为10−6 m/s，即24 h内累积降雨86.4 mm(从气象学角度定义为暴雨)，设定降雨时间从一般状态下的20~50 h延长至120 h，从而体现长期强降雨对深部土体的影响规律。

在非饱和土的研究进程中，FREDLUND等[14]提出了一些土水特征曲线的表达式，本文采用VAN GENUCHTEN[15]于1980年所提出的土水特征曲线计算模型和渗透系数函数曲线计算模型：

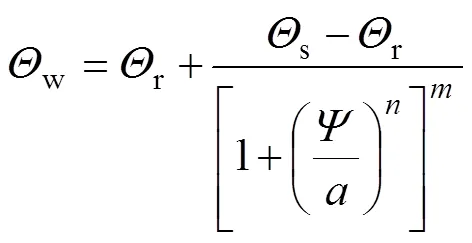
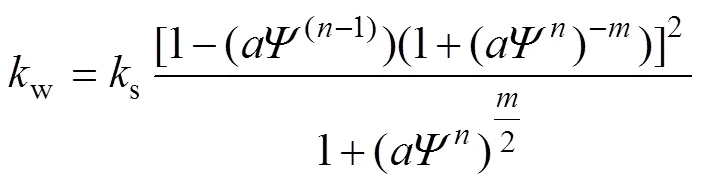
式中：w为含水率；r为残余含水率；s为饱和含水率；w为渗透系数；s为饱和渗透系数；，和为曲线拟合参数；=1/(1−)；为基质吸力。采用式(3)和(4)拟合土水特征曲线与渗透系数函数，结果分别如图2和图3所示。不同土质的土水特征曲线参数如表2所示。

(a) 黏土；(b) 粉土；(c) 砂土

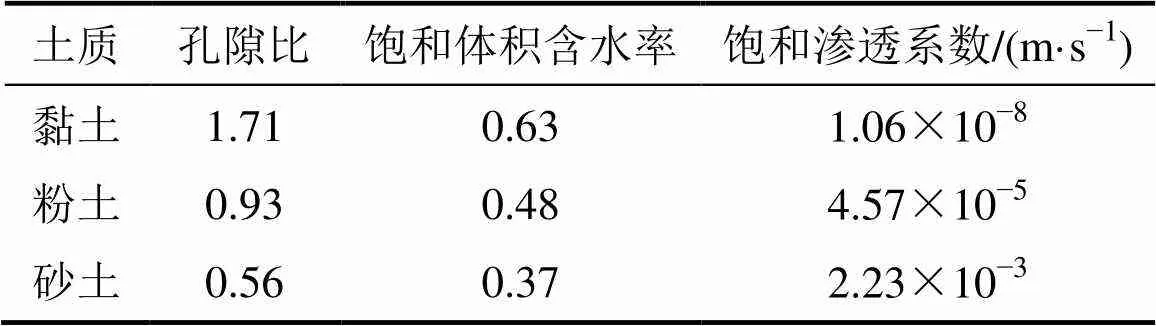
表1 不同土质渗透性参数计算取值

采用专业的岩土工程有限元分析软件Geo-studio进行计算，所建有限元模型如图4所示。一维模型高为10.00 m，宽为3.00 m，0 m处为地下水位线；网格划分为：6 m以下单元高度为0.50 m，6.00~9.00 m范围内的网格高度设定为0.25 m，9.00~9.80 m范围内网格高度设置为0.10 m，9.80~10.00 m网格高度设置为0.05 m。对于二维边坡，设定边坡坡比为1.0:2.0，1.0:1.5和1.0:1.0共3种状况，边坡垂直厚度为10.00 m，各高程的网格密度划分与一维模型的相同。设定最大迭代步数为100次，计算结果表明每个计算步均在100次迭代内收敛。

在一维模型中，以模型中部截面为监测截面，在二维边坡模型的上、中、下部各设定1个截面，用于分析坡度对边坡含水率分布的影响。在分析过程中，首先对模型表面的初始基质吸力进行稳态分析，得到土体内部的初始含水率分布，然后，在土体表面设定单位流量边界模拟降雨过程(当单位流量大于渗透系数时则自动转化为水头边界)，计算时间为120 h。大量前期研究成果表明[16−17]：在进行边坡渗流分析时，可将模型的底部和两侧边界设定为不透水边界。具体的一维、二维计算方案如下：边坡坡比为1.0:2.0，1.0:1.5和1.0:1.0；土质为黏土、粉土和砂土；初始表面吸力为10，100和500 kPa；降雨强度为1×10−6 m/s；降雨时间为0~120 h。

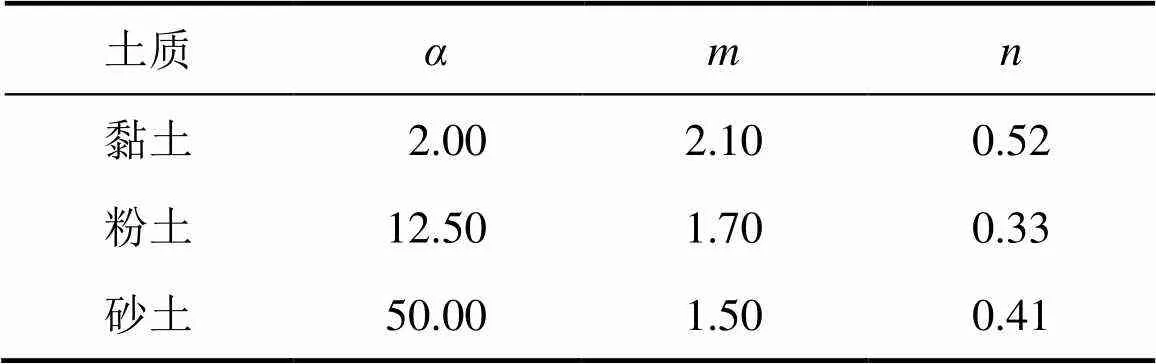
表2 不同土质土水特征曲线参数值

1—黏土；2—粉土；3—砂土。

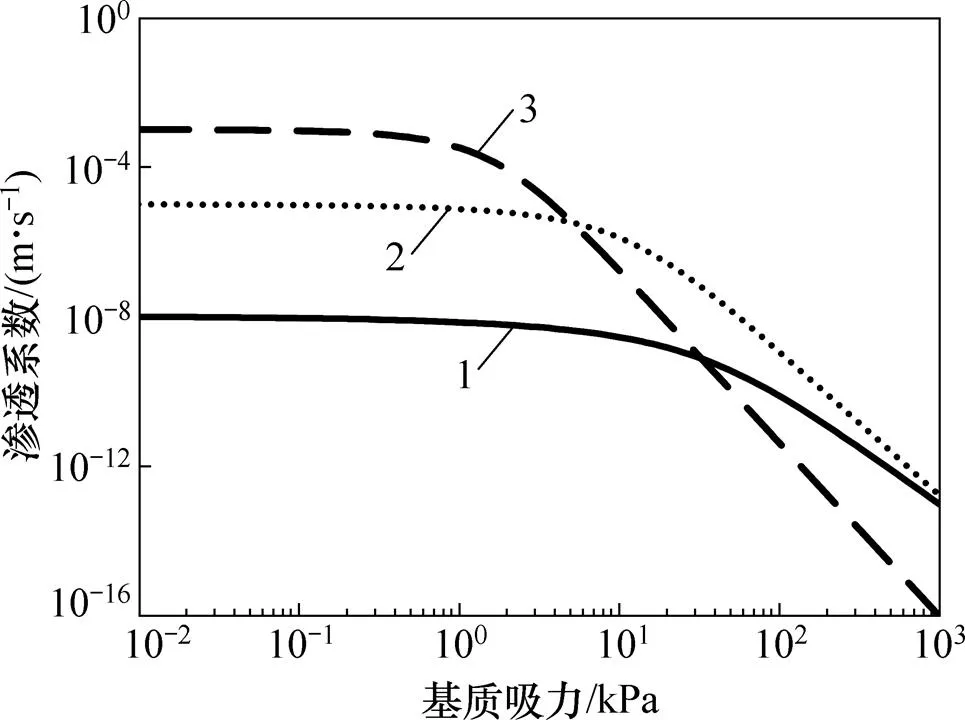
1—黏土；2—粉土；3—砂土。

(a) 一维渗透模型；(b) 二维渗透模型

3 计算结果与分析

3.1 一维分析

通过对一维模型进行计算，从而确定初始表面吸力、土质以及降雨时间等因素对降雨入渗过程及饱和区分布的影响。在分析时将降雨过程中，含水率达到90%以上的区域定义为饱和区[16, 18]，且为了便于分析，定义与降雨强度等值的渗透系数所对应的含水率为等降雨强度含水率。

不同条件下降雨入渗深度与饱和区分布见图5。从图5(a)~(c)可见：在黏土初始表面吸力为500 kPa时，降雨入渗深度并没有随降雨时间的推移而显著增加，降雨120 h后降雨入渗深度约为0.60 m，且在0.60 m深度内均为饱和区；当土体表面初始吸力降至100 kPa时，降雨入渗深度仍较小，且降雨入渗区域内均为饱和状态；当初始表面吸力为10 kPa时，黏土的初始含水率已经基本趋于饱和，但降雨对含水率依然有影响；当降雨时间达到120 h时，降雨入渗深度为1.00 m左右。可见：对于黏土而言，降雨入渗深度较小，且在降雨入渗范围内全部呈饱和状态。这是由于黏土的饱和渗透系数明显小于降雨强度(渗透系数与降雨强度量纲相同)，无论黏土在非饱和状态下或者饱和状态下，其内部水分消散的速度远小于外部供给速度。

从图5(d)~(f)可见：当粉土的表面基质吸力为500 kPa时，降雨入渗深度随降雨时间的增大而明显增大；在降雨24 h时，降雨影响范围内呈饱和状态，但随着降雨时间延长，前期降雨形成的饱和区域逐渐消失，表面含水率逐渐趋于等降雨强度含水率；而当表面基质吸力为100 kPa时，24 h后的降雨入渗深度略有增大，但并未出现饱和区域；在降雨至120 h的过程中，土体表面含水率保持不变，可见此时降雨时间仅对入渗深度有影响；当表面吸力为10 kPa时，土体的渗透系数大于降雨强度，因此，在进行降雨计算时，土体含水率会下降至等降雨强度含水率，此时，降雨不再使表面含水率增加，而是导致地下水位上升。可见：降雨入渗对粉土的影响深度远大于黏土的影响深度；当粉土表面含水率远小于等降雨强度含水率时，边坡表面出现饱和区，反之，则引起地下水位上升。这是由于当土体处于非饱和状态时，渗透系数小于降雨强度，雨水供给速度大于雨水消散速度，导致土体表面出现饱和区域，而此时土体渗透系数逐渐增大，雨水消散速度大于供给速度，导致饱和区域消失，降雨入渗深度不断增大。当初始表面吸力对应的渗透系数大于降雨强度时，雨水则直接下渗。

从图5(g)~(i)可见：在初始表面吸力为500 kPa时，土体表面在降雨后出现明显的饱和区域；随着降雨时间增加，饱和区深度不断增大，在降雨入渗深度范围内土体均呈饱和状态，而且饱和区域与非饱和区域界面非常明显；当表面吸力为100 kPa时，砂土的降雨入渗深度随着降雨时间增加而大幅度增加；降雨24 h时，在降雨入渗深度内的区域为饱和区域，但当降雨持续进行至72 h时，表面含水率开始下降，饱和区域整体下移；而当降雨至120 h后，表面土体含水率达到某一定值不变，且原有饱和区继续下移；当表面吸力降至10 kPa时，降雨会导致砂土上部含水率提高，但并未达到饱和，随后降雨迅速入渗，降雨72 h时，基本达到地下水位线位置，而当降雨达到120 h时，地下水位开始上升。总之，当砂土表面含水率远小于等降雨强度含水率时，降雨入渗范围内的土体呈饱和状态；当表面含水率增加至等降雨强度含水率时，饱和区域开始整体下移；而当初始表面吸力继续减小时，降雨入渗则会很快导致地下水位上升。产生以上现象的主要原因是：当砂土的含水率较小时，饱和渗透系数非常小；当初始表面吸力较大时，入渗的水分难以迅速消散；而当基质吸力逐渐降低时，渗透系数便会迅速增大，导致原有饱和区底部下移，顶部消散，使饱和区域呈现整体下移趋势；当初始表面吸力较小时，短时降雨会使表面渗透系数升至与降雨强度相同，此时，雨水迅速入渗，导致地下水位上升。

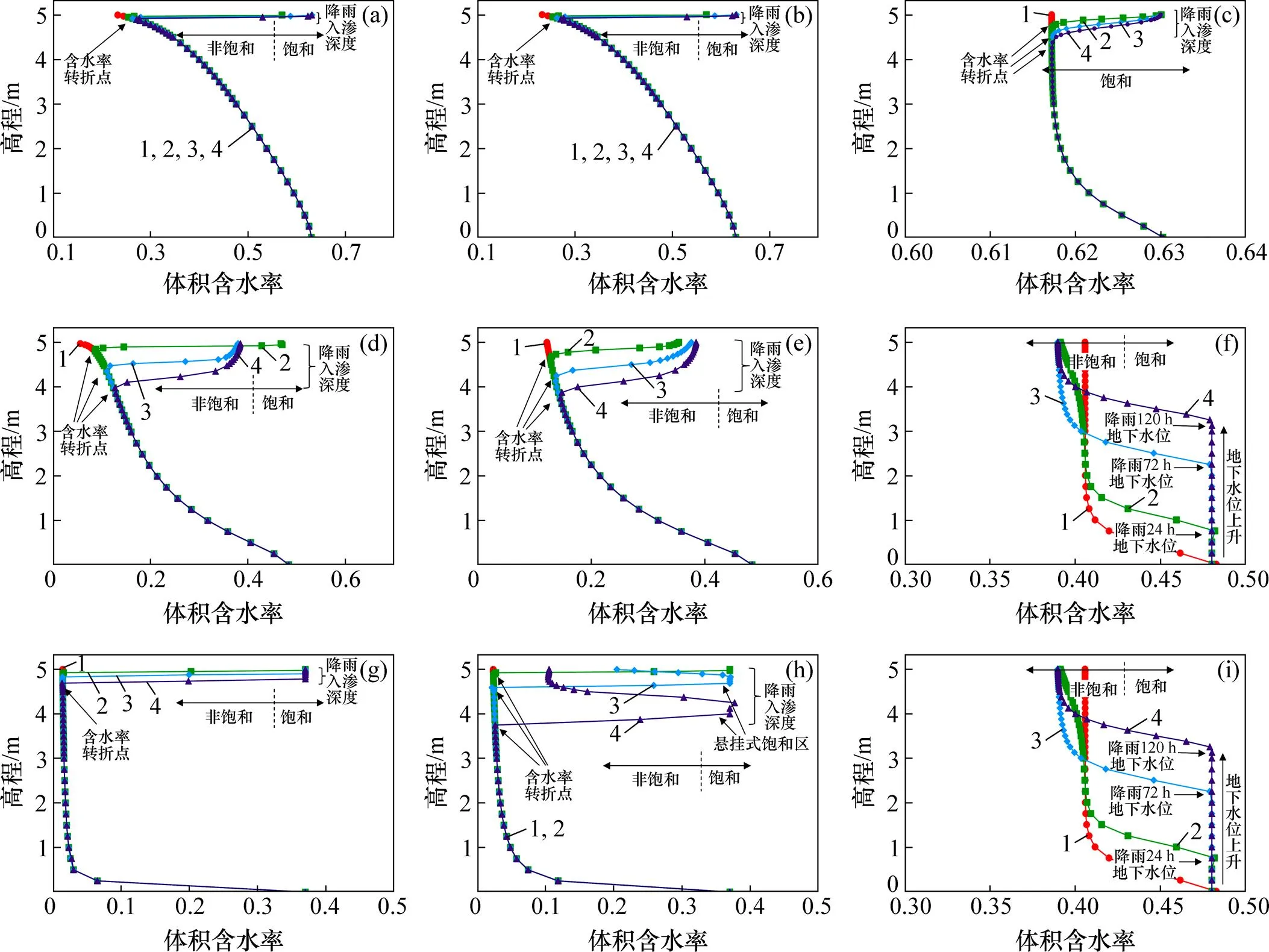
(a) 黏土，初始表面吸力为500 kPa；(b) 黏土，初始表面吸力为100 kPa；(c) 黏土，初始表面吸力为10 kPa； (d) 粉土，初始表面吸力为500 kPa；(e) 粉土，初始表面吸力为100 kPa；(f) 粉土，初始表面吸力为10 kPa； (g) 砂土，初始表面吸力为500 kPa；(h) 砂土，初始表面吸力为100 kPa；(i) 砂土，初始表面吸力为10 kPa

从图6可以看出：随着降雨时间增长，不同土质的降雨入渗深度均会有所增加，且不同时间的入渗深度与土质和初始吸力均密切相关。整体而言，对于任意1种土体，当初始土体表面吸力为100 kPa时，降雨入渗深度均明显大于初始土体表面基质吸力为500 kPa时的降雨入渗深度，这说明在同等条件下，初始表面吸力越小，降雨入渗深度越大。而在同等初始表面吸力、同等降雨时间作用下，降雨入渗深度从大至小的土质依次为粉土、砂土和黏土。

3.2 二维分析

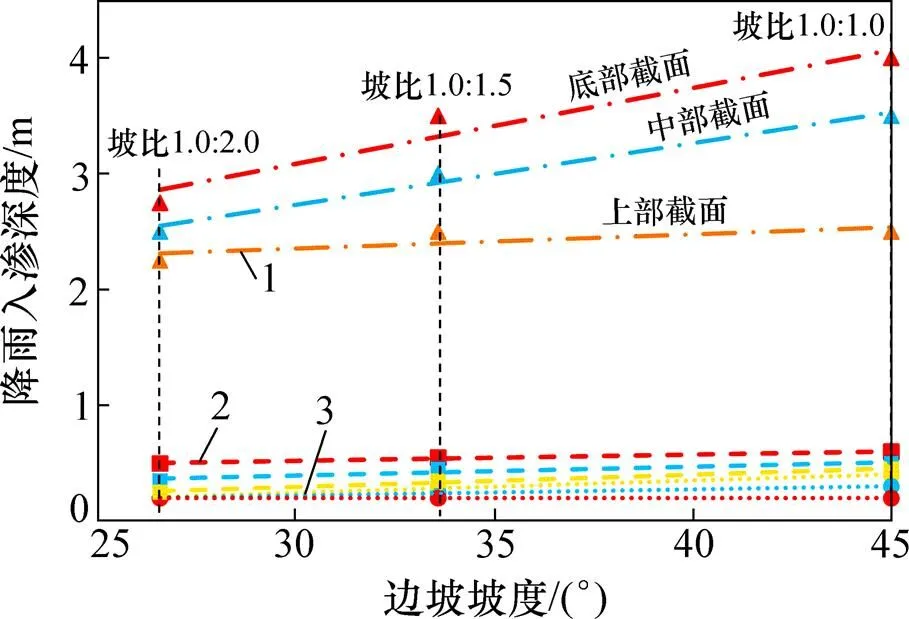
为考虑坡度对降雨入渗深度、饱和区变化状态等渗流特性的影响，建立二维计算模型，得到不同状态下的边坡渗流特征，如图7所示。从图7可以看出：在500 kPa初始表面吸力状态下，降雨120 h时粉土任意截面的降雨入渗深度均比其他2种土质的大，底部、中部截面的降雨入渗深度随边坡坡度的增大而显著增大。对于黏土和砂土，砂土的降雨入渗深度大于黏土的降雨入渗深度，但边坡坡度对各个截面的降雨入渗深度基本没有影响。通过分析一维渗流状态可知出现以上规律的原因为：在表面初始基质吸力为500 kPa时，在3种土质中，粉土的降雨入渗深度最大；而对于不同坡度，当边坡坡度增大时，上部的雨水在重力作用下进一步从上部向下部入渗，导致边坡中下部受降雨影响更加明显。

强降雨导致边坡失稳最重要的原因之一是坡脚处降雨入渗深度增加，引起土体孔隙水压力上升，有效应力下降，进而导致土体的抗剪强度下降，最终坡脚处首先发生滑移[19]。因此，进一步分析边坡底部截面在降雨影响下的含水率分布十分必要。

考虑黏土在不同初始表面吸力以及不同边坡坡度状态下，坡脚处的降雨入渗深度与降雨时间的关系如图8所示。从图8可知：底面降雨入渗深度受边坡初始表面吸力的影响最大；当表面吸力为10 kPa时，降雨入渗深度远大于初始表面吸力为100 kPa和500 kPa时的入渗深度；当初始表面吸力为100 kPa时，底部截面降雨入渗深度降至0.2~0.6 m；当初始表面吸力增加至500 kPa时，底部截面最大降雨入渗深度仅为 0.2 m左右，可以认为此时底面降雨入渗深度受降雨时间影响极小。对比分析边坡坡度的影响可以发现：坡度为1.0:1.0时的黏土边坡底部截面降雨入渗深度比坡度为1.0:1.5及1.0:2.0的边坡的降雨入渗深度大，这种影响在初始表面吸力为10 kPa与100 kPa时最明显；随着初始表面吸力增加，边坡坡度对坡面底部截面降雨入渗深度的影响也逐渐下降；当边坡表面初始基质吸力达到500 kPa时，边坡坡度对底部截面降雨入渗深度基本没有影响。

1—粉土，初始表面吸力100 kPa；2—砂土，初始表面吸力100 kPa；3—黏土，初始表面吸力10 kPa；4—粉土，初始表面吸力500 kPa；5—砂土，初始表面吸力500 kPa；6—黏土，初始表面吸力100 kPa；7—黏土，初始表面吸力500 kPa。

1—粉土边坡；2—砂土边坡；3—黏土边坡。

图8 黏土边坡底面截面降雨入渗深度变化规律

在一维分析中，砂土在初始表面基质吸力为 100 kPa时的渗流规律与其他条件下的渗流规律明显不同，其在降雨持续过程中不仅在土体表面出现饱和区，而且饱和区随着时间的推移不断下降，上、下部均呈非饱和状态，形成悬挂状的饱和区。应将此种状态扩展至二维状态下进行分析，探究饱和区在二维砂土质边坡中的变化规律。

在100 kPa初始表面吸力状态下，砂土边坡饱和区下移过程如图9所示。以边坡坡度为1.0:2.0为例，初始状态下边坡含水率分布与一维状态的边坡含水率分布基本相似，从边坡表面至边坡中部含水率基本保持不变；当降雨持续24 h时，仅边坡表面向下0.2 m处受降雨影响；当降雨达到48 h时，雨水入渗至边坡表面向下0.5~1.0 m处，而且由于存在坡度，边坡上部雨水沿表面湿润区域向下渗流，导致边坡上部受雨水影响明显比边坡底部的小；当降雨72 h时，边坡表面含水率开始下降，明显出现内部悬挂式的饱和区，而且在边坡上部水分下渗的影响下，坡脚处开始形成大面积饱和区；当持续降雨96 h时，悬挂式饱和区逐渐下移，边坡内部降雨入渗深度增加，坡面底部饱和区进一步增大；当降雨120 h时，边坡内部饱和区继续下移，坡脚处的饱和区达到最大。由此可知：受坡度的影响，由坡面入渗的雨水会沿着表面的饱和区从上至下渗流，最终流动至边坡底面处，导致边坡坡脚处饱和区域范围扩大，进而导致边坡易发生浅层滑动。

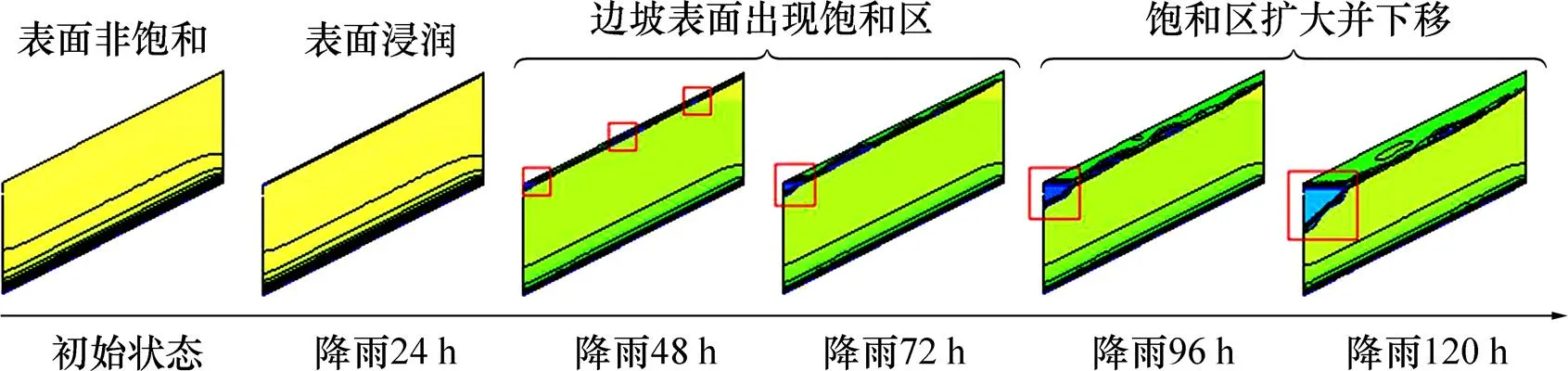
图9 100 kPa初始表面吸力状态下砂土边坡饱和区下移过程

图10 10 kPa初始表面吸力状态下粉土边坡地下水位抬升过程

一维分析结果表明：在粉土的表面初始吸力降至10 kPa时，强降雨会直接导致边坡内部水位线上升，并且不会出现饱和区域。而徐则民等[20]认为强降雨导致的地下水位上升会直接引起边坡深层失稳，因此，对此种状态下的渗流特征进行二维分析也具有重要 意义。

在降雨0~30 h过程中，粉土在初始表面吸力为10 kPa状态下的边坡地下水位上升过程见图10。从图10可以看出：在降雨开始后，地下水位随即明显上升；当降雨12 h时，边坡坡度对地下水位线分布的影响开始显现；在降雨18~30 h期间，边坡坡脚处的水位线高度明显比边坡上部的高；在降雨达到30 h时，边坡坡脚处地下水位升至6 m左右，而边坡上部地下水位高度仅为2 m。在真实状态下，边坡坡脚处必定设有排水措施，可以将入渗的水分排出，但当防护措施不当导致排水效果不明显时，一旦排水状态下的单位流量小于降雨强度，则会引起坡脚处地下水位快速上升，易引发边坡深层滑动。

4 结论

1) 不同土质在不同表面基质吸力条件下，降雨入渗深度差异明显，具体表现为初始表面吸力越小，降雨入渗深度越大。在同等条件下，降雨入渗深度从大至小的土质依次为粉土、砂土和黏土。

2) 黏土在降雨入渗深度内的范围均为饱和区域；粉土在降雨过程前期会出现饱和区，随后饱和区域消散；砂土在降雨前期的入渗范围即为饱和区；随着降雨持续，饱和区逐渐下移，形成悬挂式饱和区。

3) 受边坡坡度的影响，在同等初始表面吸力下，坡度越大，边坡底部的降雨入渗深度越大，且粉土边坡受坡度影响更明显。边坡初始表面吸力越小，边坡底部截面降雨入渗深度越大。

4) 当初始表面吸力为100 kPa时，砂土边坡在降雨过程中逐渐出现饱和区；随着降雨时间推移，饱和区增大并逐渐向坡脚处移动。当初始表面吸力为 10 kPa时，粉土边坡在降雨作用下，地下水位不断上升，且坡脚处地下水位高度明显比边坡其他区域的高。

[1] 连继峰, 罗强, 蒋良潍, 等.顺坡渗流条件下土质边坡浅层稳定分析[J]. 岩土工程学报, 2015, 37(8): 1440−1448. LIAN Jifeng, LUO Qiang, JIANG Liangwei, et al. Shallow stability analysis of soil slopes under seepage parallel to slope surface[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1440−1448.

[2] 周建烽, 王均星, 陈炜.非饱和非稳定渗流作用下边坡稳定的有限元塑性极限分析下限法[J]. 岩土工程学报, 2014, 36(12): 2300−2305. ZHOU Jianfeng, WANG Junxing, CHEN Wei. Lower bound analysis of slope stability subjected to transient unsaturated seepage[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(12): 2300−2305.

[3] 王成华, 万正义, 张成林.非饱和砂土坡面降雨非正交入渗试验与数值模拟研究[J]. 岩土工程学报, 2015, 37(8): 1357−1364. WANG Chenghua, WAN Zhengyi, ZHANG Chenglin. Tests and numerical simulations of non-orthogonal rainfall infiltration on surfaces of unsaturated sand slopes[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1357−1364.

[4] YEH H F, WANG J, SHEN K L, et al. Rainfall characteristics for anisotropic conductivity of unsaturated soil slopes[J]. Environmental Earth Sciences, 2015, 73(12): 8669−8681.

[5] 刘晓, 张杰, 王涛, 等.积水条件下夹砂层土质边坡的稳定性分析[J]. 地下空间与工程学报, 2015, 11(S1): 288−294, 301. LIU Xiao, ZHANG Jie, WANG Tao, et al. Stability analysis of soil slope with sand layer under water conditions[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(S1): 288−294, 301.

[6] PEDROSO D M. A solution to transient seepage in unsaturated porous media[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 285: 791−816.

[7] 王智磊, 孙红月, 刘永莉, 等.降雨与边坡地下水位关系的时间序列分析[J]. 浙江大学学报(工学版), 2011, 45(7): 1301−1307. WANG Zhilei, SUN Hongyue, LIU Yongli, et al. Time series analysis about groundwater level in slope and rainfall[J]. Journal of Zhejiang University(Engineering Science), 2011, 45(7): 1301−1307.

[8] BANDARA S, FERRARI A, LALOUI L. Modelling landslides in unsaturated slopes subjected to rainfall infiltration using material point method[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2016, 40(9): 1358−1380.

[9] SUNG E C. Stability Analysis of unsaturated soil slopes considering water-air flow caused by rainfall infiltration[J]. Engineering Geology, 2016, 211: 184−197.

[10] 付宏渊, 曾铃, 王桂尧, 等.降雨入渗条件下软岩边坡稳定性分析[J]. 岩土力学, 2012, 33(8): 2359−2365. FU Hongyuan, ZENG Ling, WANG Guiyao, et al. Stability analysis of soft rock slope under rainfall infiltration[J]. Rock and Soil Mechanics, 2012, 33(8): 2359−2365.

[11] 曾铃, 付宏渊, 周功科.降雨入渗参数对粗粒土路堤暂态饱和区影响的数值模拟[J]. 河海大学学报(自然科学版), 2014, 42(3): 250−256. ZENG Ling, FU Hongyuan, ZHOU Gongke. Numerical simulation of effects of rainfall infiltration parameters on transient saturated areas of coarse-grained soil embankment[J]. Journal of Hohai University(Natural Sciences), 2014, 42(3): 250−256.

[12] 顾慰慈.渗流计算原理及应用[M]. 北京: 中国建材工业出版社, 2000: 10−22. GU Weici. Principle and application of seepage calculation[M]. Beijing: China Building Materials Industry Press, 2000: 10−22.

[13] JOHN K. Seep modeling with SEEP/W2007 version[R]. Calgary, Canada: Geoslope International Ltd., 2008: 266−268.

[14] FREDLUND D G, MORGENSTERN N R, WIDGER R A. Shear strength of unsaturated soils[J]. Canadian Geotechnical Journal, 1978, 15(3): 313−321.

[15] VAN GENUCHTEN M T. A closed form equation for prediction the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of American Journal, 1980, 44(5): 892−898.

[16] ZENG L, BIAN H B, SHI Z N, et al. Forming condition of transient saturated zone and its distribution in residual slope under rainfall conditions[J]. Journal of Central South University, 2017, 24(8): 1866−1880.

[17] 马吉倩, 付宏渊, 王桂尧, 等. 降雨条件下成层土质边坡的渗流特征[J]. 中南大学学报(自然科学版), 2018, 49(2): 464−471. MA Jiqian, FU Hongyuan, WANG Guiyao, et al. Seepage characteristics of layered soil slope under rainfall conditions[J]. Journal of Central South University(Science and Technology), 2018, 49(2): 464−471.

[18] SHAKOOR A, SMITHMYER A J. An analysis of storm-induced land-slides in colluvial soils overlying mudrock sequences, southeastern Ohio, USA[J]. Engineering Geology, 2005, 78(3/4): 257−274.

[19] 詹良通, 刘小川, 泰培, 等.降雨诱发粉土边坡失稳的离心模型试验及雨强–历时警戒曲线的验证[J]. 岩土工程学报, 2014, 36(10): 1784−1790. ZHAN Liangtong, LIU Xiaochuan, TAI Pei, et al. Centrifuge modelling of rainfall-induced slope failure in silty soils and validation of intensity-duration curves[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(10): 1784−1790.

[20] 徐则民, 黄润秋.山区流域高盖度斜坡对极端降雨事件的地下水响应[J]. 地球科学进展, 2011, 26(6): 598−607. XU Zemin, HUANG Runqiu. The response of the groundwater in vegetated slopes in mountainous catchments to heavy rain events[J]. Advances in Earth Science, 2011, 26(6): 598−607.

Variation law of rainfall infiltration depth and saturation zone of soil slope

LIU Jie1, 2, ZENG Ling3, FU Hongyuan2, 3, SHI Zhenning2, ZHANG Yongjie3

(1. Engineering Research Center of Catastrophic Prophylaxis and Treatment of Road & Traffic Safety of Ministry of Education, Changsha University of Science & Technology, Changsha 410114, China; 2. School of Traffic & Transportation Engineering, Changsha University of Science & Technology, Changsha 410114, China; 3. School of Civil Engineering, Changsha University of Science & Technology, Changsha 410114, China)

1-D and a 2-D models were established to analyze the variation of rainfall infiltration depth and saturation zone of slope with different rainfall conditions, soil types, surface matric suctions and slope ratios based on the finite element calculation theory of saturated-unsaturated seepage. The results show that soil with smaller initial surface suction has greater rainfall infiltration depth, and silt, sand and clay follow the large-to-small order in the rainfall infiltration depth. During rainfall process, the clay is saturated in the rainfall infiltration area, while silt is saturated in the infiltration area at first and then the saturation zone dissipates. As for sand, the saturation zone forms in the rainfall infiltration area firstly, then it moves down and forms a suspended saturation zone. The greater slope ratio leads to greater rainfall infiltration depth in the middle and bottom of slope, and the influence of the slope ratio on the silty slope is more obvious. Under the action of rainfall, the saturation zone forms on the surface of sandy slope and then it expands and moves down. The silt slope with small initial surface suction will directly lead to the increase of groundwater level under rainfall.

soil slope; rainfall infiltration; infiltration depth; saturation zone

10.11817/j.issn.1672−7207.2019.02.026

TU42

A

1672−7207(2019)02−0452−08

2018−05−25；

2018−07−12

国家自然科学基金资助项目(51838001，51878070，51578079，51678074)；湖南省教育厅优秀青年基金资助项目(17B013，15B103)；湖南省研究生科研创新项目(CX2018B528)；长沙理工大学道路灾变防治及交通安全教育部工程研究中心开放基金资助项目(kfj170404)(Projects(51838001, 51878070, 51578079, 51678074) supported by the National Natural Science Foundation of China; Projects(17B013, 15B103) supported by the Outstanding Youth Project of Education Department of Hunan Province; Project(CX2018B528) supported by the Postgraduate Research and Innovation Fund of Hunan Province; Project(kfj170404) supported by the Open Fund of Engineering Research Center of Catastrophic Prophylaxis and Treatment of Road & Traffic Safety of Ministry of Education (Changsha University of Science & Technology)

曾铃，副教授，从事边坡稳定性等研究；E-mail：zlbingqing3@126.com

(编辑 陈灿华)