公路缓和曲线测量定位的几个问题

李益强， 张坤宜,2， 速云中， 张齐周， 侯林锋

(1.广东工贸职业技术学院 测绘遥感信息工程系，广东 广州 510510； 2.广东工业大学 离退休处老教授协会，广东 广州 510090)

1 关于缓和曲线特征模式

缓和曲线是当前测量定位公路路线曲线所涉及的主要内容之一，主要是道路学科用于描述车辆运行曲线的一种专业术语。缓和曲线主要是指位于某点的曲率1/ρ和此点与原点之间的曲线距离lρ，两者之间成正比，并且是均匀增大的曲线。基本公式如下：

或A2=ρlρ

(1)

式中A表示的是缓和曲线参数，也被称之为回旋曲线系数，此公式是针对缓和曲线的特征表达式。

如图1所示，沿直线mn方向，当位于点T1时，缓和曲线的曲率半径为∞；T2与T1之间的弧长表示为lρ，ρ表示的是曲率半径，弧长lρ与曲率半径ρ之间的关系，就可满足公式(1)。通过延伸弧长lρ直到T3点时，弧长表示为l，据公式(1)，可得

A2=Rl

(2)

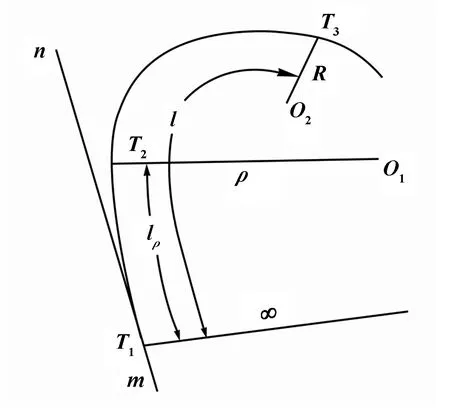
图1 缓和曲线T1-T2-T3

2 关于常规缓圆曲线的缓和曲线弧长

从缓和曲线定义角度来说，公式(1)、(2)并不属于缓和曲线方程，只是概念性的对缓和曲线特征形成的一种表述。对公式(1)、(2)的具体应用方面来讲，因为A本身是未知的，所以单纯使用公式(2)并不能为缓和曲线弧长l的求解提供方便。并且在A、l未知的情况下，将公式(2)用于求解缓和曲线，就会失去解题意义。

虽然曲线弧长在应用公式(2)进行求解的情况下不存在任何意义，但无法使缓和曲线弧长对常规缓圆曲线在高速公路定位中的应用造成任何影响。

图2就是典型的一种常规缓圆曲线图形，整条缓圆曲线由直线MA开始至直线BN结束，经由C、D、B点后，形成由缓和曲线AC、缓和曲线DB以及圆曲线CD所组成的线形结构。常规缓圆曲线主要在单一路线转弯曲线的设计中应用。其中DB弧长l为已知条件、圆曲线半径R、缓和曲线AC也是已知的，且二条缓和曲线具有等距弧长；在数学模式下的线型定位中，部分参数模数为固定的，需要使用规范标准化，例如圆曲线偏移值p以及点位坐标x、y等参数。

图2 常规型缓圆曲线

缓和曲线AC、DB弧长l为已知状态是常规缓圆曲线定位具有的主要特点，使曲线定位计算更加方便。因此，当缓和曲线弧长长度已知的情况下，为了计算方面，在常规缓圆曲线定位中即可使用缓和曲线弧长。

3 关于应用缓和曲线弧长的麻烦

现代交通路线，因为实际地形以及线路等级的影响，多为非常规缓圆曲线，具有多样性的曲线线形结构，曲线组合形状不同，曲线长短也存在较大差异，在立交互通道路工程体现的尤为明显，曲线组合形状缺乏固定模式，复杂多变，所以缓和曲线的弧长长度也就是未知的，所以缓和曲线弧长在非常规缓圆曲线中的实际应用成为了难题。如图1所示，想要将缓和曲线接入到半径为R的圆曲线与直线mn之间，缓和曲线弧长l就需要是已知的。使用缓和曲线弧长开展测量定位工作，首先需将接入弧长l的长度进行精确计算。

公式(2)是对缓和曲线弧长实施计算的传统方法，首先需要设计圆曲线半径R，再对A进行预设，最后求得缓和曲线弧长l。

此种传统的计算方法虽然看似较为简单，但是为什么会在以上叙述中，将缓和曲线弧长在非常规型缓圆曲线中的应用，称之为一个长期存在的难题呢？综合多方面研究分析发现，参数A的预设才是问题与麻烦产生的根本原因。具体表现如下：

(1)反复多次的设定参数A。预设A后，若所求的缓和曲线弧长l无法满足要求的情况下，则为无效预设，为了求得满足要求的缓和曲线弧长l，就需要对参数A进行反复预设。

(1)参数A求得较难。参数A在公式(1)以及公式(2)中均为系数，如果将公式(2)用于求取缓和曲线，就需要保证参数A为已知的。A在道路学科中专业系数，与车辆运行所涉及的多种参数均存在相关性，获得较难，通常情况下需要依靠经验进行设定。在曲线复杂多变的组合形状影响下，导致系数A也同样具有多变性，规范上设置了针对性的系数A限制条件，但是在实际应用过程中较难掌握。

(3)“存在多重、繁琐计算”。在求缓和曲线弧长l时，需要对系数A进行预设，旧货相应增加多种数学方法以及条件限制，最后实施检验考察。当未得出结果，则需要开展多重计算，计算过程也较为繁琐。

(4)存在计算、预测不准的可能。算不准、测不准是缓和曲线弧长早期计算的显著问题，路线断线、错位会经常性的出现，分析此种问题主要产生的原因是，所预设的系数A具有误差，使自动化以及通用性定位等方面的应用产生障碍。

(5)实际应用的便利性较差。系数A的精准预设难度较大，专业人士也很难一次性获取精确的预设值。而当重新定位、调整路线的情况下，非专业人士很难对系统A进行预设，难以实现系数A的设定与应用。

从上述问题说明，在路线曲线定位过程中，系数A的设定是一个历史性难题，对曲线定位使用有关系数A进行设定的方案只能作为权宜之计，而无法良好使缓和曲线定位过程中的难题得到良好解决。

4 缓和曲线弧长方程

缓圆曲线在测地线(大地线)理论下具有密切特征，所以缓和曲线同样具有。因此通过结合缓和曲线圆弧距表达式，对缓和曲线弧长方程使用反分析原理实施推证，可得

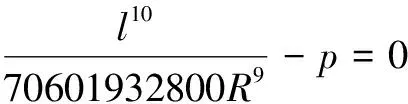
(3)

公式(3)表明，已知半径R、p，缓和曲线长度l就会使方程的要求得到满足。简化公式(3)可得缓和曲线弧长方程，即

(4)

公式(4)中，lo=l2；系数A、B、C、D、E与圆曲线半径R存在明确的关系，即

(5)

公式(4)中，A、B、C、D、E等相关系数，可通过使用公式(5)，求得圆曲线半径R。

图3 缓和曲线弧长方

图3与图2的p，具有位置的相同，但是所代表的意义存在较大差别。其中图2种的p，主要指的是缓和曲线长度l，在导致圆曲线出现的偏移值，属于一种待求参数；而图3中，p代表的是圆曲线和直线之间存在的实际客观距离，属于已知参数，也是导致缓和曲线产生的主要原因，并因此称之为称为圆弧距。从图3中可以发现，圆弧距主要指的是圆弧点d直至x轴，并垂足E所形成的距离。在图3中可了解到，只要已知设计圆半径R和圆心O位置的，即可明确圆心O距离直线ZHx之间存在的距离s，圆弧距p=s-R，因此可依据公式(4)缓和曲线弧长长度l。如图4可见非对称缓圆曲线。

图4 非对称缓圆曲线

随着确定了缓和曲线弧长方程，圆弧距等相关概念的提出，使传统缓曲线长度l与p的关系得以改变。通过进一步将非常规缓圆曲线中的圆弧距p转变为已知参数，同时为了保证缓和曲线弧长长度l的准确性与安全性。但是此种方法圆弧距与非对称缓圆曲线为依据，成为能够取得缓和曲线弧长的以及曲线长度的唯一解。

5 关于缓和曲线弧长方程的应用

非对称型缓圆曲线样式结构具有多样性，在本文中的非对称型缓圆曲线形，仅用圆曲线、直线以及缓和曲线。以图4为例，对缓和曲线弧长方程在定位中的实际应用进行阐述。未知缓和曲线弧长l1、l2的长度，且弧长长度不相等是非对称型缓圆曲线结构具有的主要特点。缓和曲线弧长方程用于定位的具体步骤如下。

5.1 计算非对称缓圆曲线缓和曲线弧长

非对称型缓圆曲线计算基础为缓和曲线弧长方程，缓圆组合定位方法主要为“先有圆弧距p，之后有缓和曲线弧长l”。基本思路：首先以设计半径R为据，按照圆弧距pi实际参数，对缓和曲线弧长进行求解。弧长计算步骤如下：

(1)寻找圆弧距p。图4可获得相应的已知条件，圆曲线有半径R、po点坐标，直线MJD、JDN的点坐标和坐标方位角各有一个，故可以：

(2)通过利用po点坐标分别垂直于直线MJD、JDN的关系，可分别求得po点与直线MJD的距离s1、po点与直线JDN的距离s2；

(3)利用po点坐标垂直于MJD、JDN，可求得垂足E、F点坐标，并能够定位E、F点；

(4)获取圆弧距p1、p2，即p1=s1-R，p2=s2-R。

(5)使用弧长基础方程公式(4)，求缓和曲线弧长的精确值l1与l2。

5.2 非对称缓圆曲线的密切点定位

由图4可知，密切点(主点)A、B、C、D对非对称缓圆曲线结构关系起到决定性作用，所以在非对称缓圆曲线中，关键是要准确定位密切点。

(1)q1、q2可使用偏移值表达式求得，定位A、B点需要以E、F点为基准，用偏移值q1、q2进行定位。

(2)求C坐标，为C点定位。

(3)求CD弧长lCD：

(6)

式中α=αJDN-αMJD，αMJD、αJDN均为直线MJD、JDN的坐标方位角。

(4)求D点坐标(略)并进行定位。

5.3 算例

依据“直线为主”的设计要求，可将非对称圆缓曲线弧长的相关结构参数列出，如图4。表1所列，均为已知点，求垂足E、F的坐标，使圆弧距成为已知条件，之后计算缓圆曲线基本结构参数(m)：R=200，s=204.044，p1=4.044，l1=139.622，q1=69.529；s=202.086，p2=2.086，l2=100.171，q2=49.981，圆曲线弧长l=279.616。缓和曲线弧长l1、l2值得到精确后，即可获得起点A、终点B的坐标及里程等相关的结构参数。见表1。

表1 以已知点求垂足、起点、终点基本参数

6 关于缓和曲线弧长方程的结论

从理论及相关实践试验结果中可发现，缓和曲线弧长方程在路线测量定位中发挥着重要作用，在现代交通路线建设过程中的勘查设计、安全检查等工作中也得到广泛应用，并且可对技术进步发挥促进作用，缓和曲线弧长方程极具历史与现实意义。

(1)公式(4)在现代交通路线建设过程中，是一种较为常用的缓和曲线弧长方程。缓和曲线弧长具有可求性，由此可形成缓和曲线弧长方程，现代交通路线缺少缓和曲线弧长的历史得以结束。

(2)公式(1)、(2)中，系数A具有多种用途，可实现车辆曲线运行分析。但是在求取缓和曲线弧长过程中存在的困扰仍然无法得以完全避免。通过颠倒了长度l与圆弧距p的关系，让传统的统缓和曲线的圆弧距p可得，使系数A求得困难的情况得以有效解决。通过与实际相结合，缓和，遵循“圆弧距对应缓和曲线弧长”的弧长是唯一解求解原则，使缓和曲线弧长求解需要依赖预设系数A的难度得到彻底解决。

(3)应用于现代交通路线的缓和曲线弧长方程，会出现各种形式的缓圆曲线组合定位，改变传统，并建立了创新方法，简化了定位密切点以及计算弧长的相关步骤，易于掌握。

(4)缓和曲线弧长方程应用于曲线设计以及测量定位自动化等方面均具有独特优势，且具有通用性、高精度的特点，具有推广使用价值。