金融安全背景下的证券市场稳定测度新方法

欧阳天皓 卢晓勇

作者简介：欧阳天皓（1988—），男，江西南昌人，南昌大学管理学院管理科学与工程博士研究生，研究方向：金融市场，宏观经济，应用伦理。

摘要：我国证券市场经过数十年的发展，在不断的探索中渐渐成熟，但与发达国家的股票市场相比，还有不完善的地方。如我国证券市场的市值，并没有较好地与经济增长同比增长及契合实体经济的发展。通过研究20022017年的历史数据，使用支持向量机（SVM）预测证券市场的价格变化，通过误差统计分析，得出我国市场（上证交易所）与美国证券市场（纳斯达克综合指数）相比，更具不稳定性的结论。因此，可以利用套利价值（VaP）作为一种直观度量市场成熟度的参考指标。

关键词： 套利价值;有效市场假说;支持向量机;证券市场;SVM; VaP

中图分类号：F831文献标识码：A文章编号：1003-7217（2019）01-0077-07

从20世纪80年代的证券市场试点，到90年代初正式确立，我国股票市场已经有近30年的历史。期间市场有过重大的波动，也经历过重大调整。2000年后我国股市趋于稳定，总体来看，市值的大方向是向上的。股票市场已经成为我国最为重要的投资、融资渠道之一。

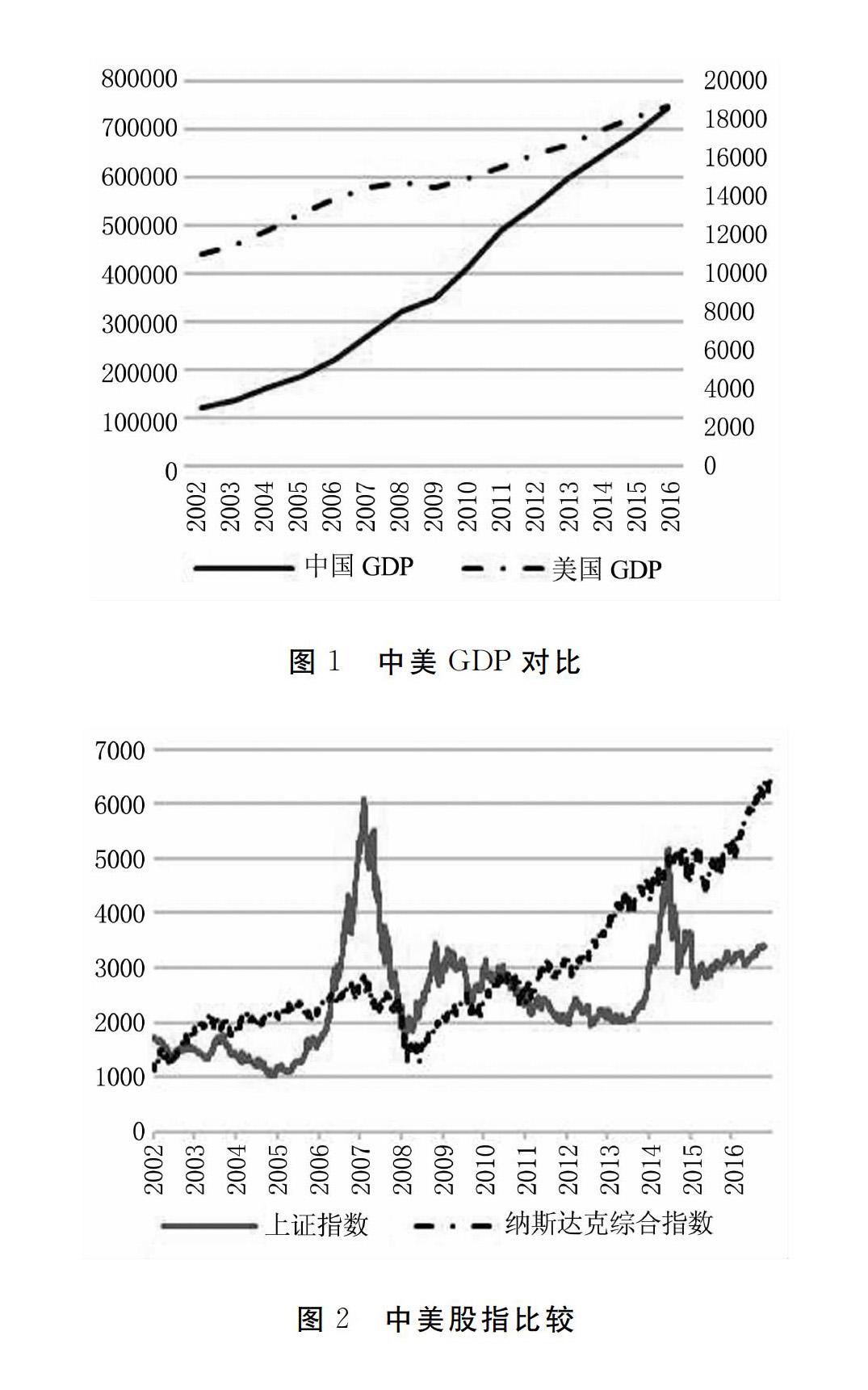
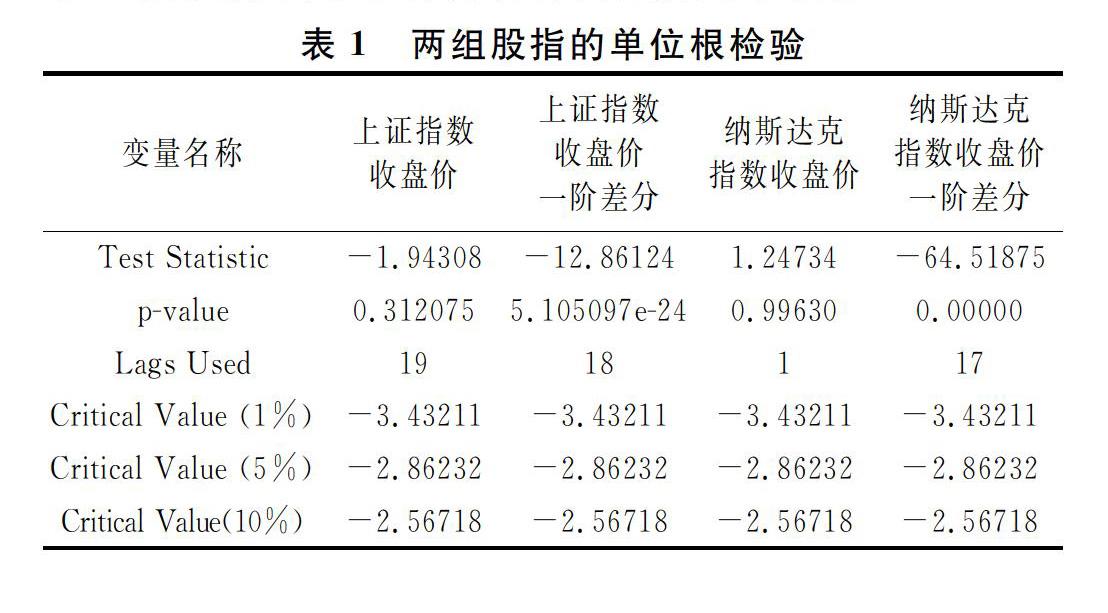
但我国股市由于种种原因，发展得还并不成熟。若以2000年后和中国入世为观察起点，可以发现其一个重要的问题是未能反映经济增长。从图1可以看到，我国GDP自2002年起呈稳步增长的态势，而美国GDP由于2008的金融危机有一个经济停滞的区间，2010年从衰退中走出后，美国经济才继续增长①。图2显示了上证指数与纳斯达克综合指数在相同时间段内的表现②，可以发现美国股指在2008年危机中受到重挫，但随着经济复苏而稳步成长。中国股市在20072008年和20142015年有两个剧烈的牛熊市，表现得非常不稳定。从数值看，美国2016年和2002年GDP的比值约1.7，而中国为7.1左右。股指按同样算法，纳斯

达克指数相对2002年的比值是5.5，同期上证指数是1.7左右。可以发现美国的股票市场走势较好地契合了经济增长态势，而中国股市的成长远远落后于经济增长。

虽然有很多可能的缘由，如政策市因素、其他金融产品吸引了资金等，来解释中国股市近十多年来两个非常突兀的牛熊市，以及总市值增长落后于经济成长。但不容否认的是，我国证券市场的走势表

现确实不如成熟经济体的证券市场那样稳定。而其不稳定性，是投资者（个人或机构）都可能最为担忧的问题。虽然证券市场流动性强，但是涨跌的大起大落及突如其来的行情转换，对投资者的资金安全都是不小的挑战，也不利于长期投资信心的建立。而且金融市场其本身的高流动性也存在风险传导到其他市场（如债券市场、外汇市场等），因此有必要继续对我国证券市场的风险及波动进行细致观察研究。

一、文献综述

对于市场成熟稳定的研究，一直是经济金融研究的热点，很多注重于价格稳定性或稳定的走势。因为对投资者来说，具有稳定走势的市场可以给投资带来稳定的收益。随着对微观理论研究的深入，文献研究更加注重与对市场的模式及运行状态的分析。其中较为重要的是法马（Eugene Fama）在20世纪70年代提出的有效市场假说，其已经成为金融理论中重要部分[1]。有效市场理论把市场按照其有效性进行了划分：从弱式效率（Weak Form Efficiency）到强式效率（Strong Form Efficiency），市场价格对信息的囊括是逐渐上升的，因此基于历史价格信息（在弱式效率下，通过“技术分析”）或内幕信息（在强式效率下）预测未来价格是较难的。但总体来说，每个市场都具有噪音交易者（Noise Trader），若没有的話，每个交易者都具有了充足的信息，则不可能撮合买卖交易，自然价格也不会出现波动。这和股票市场及其他金融市场的高度波动性情况不符。因此，对市场进行预测是可行的一种市场评估方式。可以对市场套利行为进行模拟，进而能在市场成熟度光谱上对不同的市场进行比较。

在金融研究中，计量是一种主流的方法，有很多股票市场价格预测的研究使用计量方法，在此不一一赘述[2，3]。一般来说，股票市场具有剧烈的波动性，也可以称之为非线性。因此线性的计量方法并不能很好地捕捉市场信息，来预测价格未来走势。很多研究把计量方法作为预测效果对比的基准，比如使用较新的人工智能方法，如神经网络方法等[4]。随着人工智能研究逐渐成熟，从20世纪90年代开始，新方法逐渐被用于预测市场价格。在预测股票价格上，Kim使用神经网络（ANN）和支持矢量机方法（SVM）取得了当时较好的效果[5，6]。早期受限于电脑性能，SVM比ANN更具有优势。Kim的文献在预测效率上，SVM的预测准确率就比ANN要高3个百分点。

但是随着电脑性能的提高和算法的进步，2000年前后，ANN算法在预测上逐渐受到重视[7]。如苏治等使用ANN对股票市场进行了预测分析[8]。因为其可以通过部署更多的神经元节点来捕捉更加复杂的模式（以股票市场为对象，就是价格随时间变化的运动模式）。同时， ANN模型其本身的可扩性更加受益于新算法，如进化算法、粒子算法[9，10]，可以在更短的时间内处理更复杂的数据/问题。所以ANN预测效率逐渐超过了SVM方法。同时，很多结合算法也在预测领域取得了良好的效果，如隐马尔可夫模型（Hidden Markov Model，HMM） [11，12]，主成分法[13，14]及决策树法[15]，等等。这些方法都各有千秋，在不同目标或功能上能取得较好的效果：主成分法可以在数据前期处理的过程中，筛去对输出影响不大的维度，可以提升整体的计算速度和精度;而隐马尔科夫模型对模式转变的捕捉效果比较好。面对不同的研究内容，灵活使用模型组合，都能较好地提升预测的效率。

本研究因为使用的数据量比较大且需要进行一步预测（onestep forecast），即每一个交易日都进行预测，故计算量较为庞大。同时一步预测时SVM的预测误差和ANN相比并没有显著的差距，所以使用SVM作为预测方法可以达到一个计算成本和精度的平衡。

二、理论分析框架

对于一个市场是否稳定，很多研究使用线性回归对市场的走势进行分析，对离散点进行统计，若划定范围（方差或方差的倍数）可以得到离散点数量及远离趋势（trend）的具体数值。但是由于金融市场波动性强，而且具有非线性的特点，使用线性方法并不能很好地捕捉、刻画市场的行为模式。因此使用一步预测，通过预测值与实际值的误差，来估计市场价格走势的稳定度。若误差大，则市场更加偏离其历史走势的趋势，更具不稳定性和风险性。

误差统计作为市场稳定性指标，可以很好地在中短期给出市场稳健的评估。此外，加入了套利分析作为一个长期市场成熟的评估指标。

首先，活跃的市场都存在噪声交易者，不然就无法撮合交易且市场价格也无法在波动中进行信息交换。这与现实中的证券二级市场相符合，世界各重要股票市场，成交量很多都达到每日百亿级别，我国的证券市场交易量总体上也呈上升趋势。因此，可以认为股票市场中的价格是有波动的，且具有套利（arbitrage）空间。

其次，一个成熟有效率的市场，其价格是包含丰富信息的，因此即使带有小道消息或内幕消息的投资者入市也难以取得很多获利。所以可以认为，相对于不那么成熟的市场，成熟的“有效市场”其套利空间会比较小。只要市场价格出现波动、漂移，市场就会快速反应，因为市场囊括了丰富、必要的信息，其价格会很快得到修正，回到其“正确”的价格。举例来说，若一个投资者得到一个信息，预估某股票A会有大涨，故大量买入，因此拉高了股票价格。但是市场有充分的信息，判断股票A价格被高估，故卖出，进而使得股价回到其正确区间。市场所掌握的信息是超过、胜于（outsmart）单独投资者的。换一个角度，在一个不那么“有效”的市场，上面所举例的投资者可能根据其信息，把股价炒高在高点获利并卖出，在市场反应过来之前套利。在一个不太“有效”的市场，修正价格过慢以及（或）修正幅度过小。反映在数值上，就是市场价格波动更为剧烈，且预测难度更大。所以通过预测价格变化的误差及通过预测值计算套利空间来考察一个市场成熟有效的程度是可行的。

接下来的问题是如何估计一个市场的可套利程度，这可以通过预测市场未来的价格来完成。通过历史数据，对市场价格进行预测，然后进行模拟交易，统计收益。对证券市场的价格进行估计，然后统计误差，进而可以衡量一个市场的有效程度。到这里似乎工作已经完成了，而不需要考察套利问题了。其实不然。对于资产风险的研究有多种测量角度。20世纪80年代风险价值（Value at Risk，VaR）被发现，基本原理是在一个置信区间内考察接下来一个资产在价格下跌中可能的损失数。这不仅在金融界而且还在学界都成为了一个重要的工具[16]。风险价值对于投资者来说一目了然且简单明了，比如按照VaR计算得出的结论一般是，接下来在95%置信区间内可能会损失15%左右。这样，投资者可以很直观地预估风险进而做出决策。

回到套利问题上，在完成了对市场历史价格的预测评估后，可以对历史区间内一段时间进行模拟，即按照一定的交易规则，进行套利交易模拟，最后统计套利收益价值。若是套利收益小，则市场较为成熟（投机较难获利），反之亦然。通过计算得出这种形式的结论比单纯的误差分析更加直接、明了，便于投资者决策者做参考。类似于价值风险，我们姑且称这种方法为套利价值（Value at Profit，VaP）。综合实验结果、分析市场稳定度可以参考图3。

（二）原始数据介绍

中国证券市场选用上海证券综合指数，即上证指数，从2002年7月1日到2017年12月6日，一共3751个日数据，包含的数据有开盘价、收盘价、最高价、最低价、成交量。美国股市选择纳斯达克综合指数，时间段同样是从2002年7月1日到2017年12月6日，样本容量为3888，包含的数据类别和上证指数一样。需要注意的是，因为美国证券市场节假日比中国的少，年平均250个交易日，稍高与中国224日的年平均交易日。故美国股指数据样本略大于上证指数的样本数量。

（三）原始数据的预处理

在文献综述中谈到，有很多种线性方法被用于资本价格的预测，较为常用的有GARCH、ARIMA等等。但是这些线性方法有一个缺点是其参数的判断与选取较为困难。由于本研究采取的策略是一步预测，即根据一段时间历史数据来预测下一个时间点的价格。因此若采用线性方法，需要每次都进行一次参数估计。而使用SVM，虽然也有参数需要设置，但可以通过模拟测试确定较好的参数，同时参数对实验的影响并不如上述的线性方法那样大。

在处理时间序列上，一般会进行平稳性检验，常使用单位根检验（unit root test 或Adfuller test），若含有单位根，时间序列则不平稳，进行回归分析可能导致伪回归。而对策则是通过逐阶的差分时间序列并进行单位根检验，直到使其平稳。

为了避免可能存在的伪回歸，我们对股指进行了单位根检验。由表1可见，经过一阶差分的股指数据的ADF值都小于显著值，而且pvalue也在显著范围内。这个结果和经济研究中的一般经验相符，即经济时间序列一阶差分后一般都会平稳。需要注意的是，这里只是对收盘价做了检验，意在用来验证时间序列性质，因此并没有对股票数据中的其他变量做检验。但是在后面的预测部分中，我们分别对原始数据和经过差分的数据进行对比，结果显示一阶差分的误差确实比原数据要小很多。

具体规则参考了“T+1”方式，规定为当日只能进行一次交易（因为只使用了日数据，所以无法提供交易日内更多的价格走向信息），可以是买，抑或是卖，价格则使用股指的点数。假如买入后的第二日，股指并没有上升到预测的最高价，则当日不交易，“空白交易日”加一记为“1日”。当“空白交易日”为3日时，则按收盘价卖出。反之，假如手中并没有买入“股指”，且预测的最低价都比实际最低价要低，就不交易并等待。当连续2日没有买入，即“空白交易日”为2时，第三日则以收盘价买入。当然，每当进行买入或卖出时，“空白交易日”就清零。这样设置的目的是模拟套利者的行为模式，即频繁地寻找机会“低买高卖”。通过收益来衡量两个市场的成熟程度。因此我们希望交易尽可能地覆盖所有交易日。最后统计套利空间是简单地把最后一日交易日的净资产除以起始位置的净资产，若最后一日持有的是股指，资产按当日最高价与最低价的中间值来计算。

具体预测的统计见表2。由于两组指数属于不同国家，市场特征不一样，直接对比误差并不合适。因此预测误差使用相对误差，即预测误差/当日指数平均点位。

四、讨论

从表2可以看到，上证指数的预测误差是大于纳斯达克综合指数的，所以其风险性是大于美国市场的。我们把相对误差之和称之为绝对稳定性，根据表2数据，上证指数的绝对稳定性是低于纳斯达克指数的。但是，上证指数的套利收益小于纳斯达克综合指数。这是否说明，因为上证指数的套利空间比纳斯达克综合指数小，所以中国的证券市场更加成熟呢？

其实不然，从平均振幅来看，振幅越大，则预测准确的难度就越大，这是显而易见的，这就像射箭，站得离箭靶越远就越难以射中靶心。但是，振幅越大，则套利投机的机会和利润就更高。在这里，振幅带来的两个作用是相反的，并不能帮助我们很好地处理振幅和收益的关系。但是，套利模型中的规则并不允许在日内进行买和卖。所以日内振幅并不影响收益。真正影响的是两个交易日之间的价格数据。而在交易模拟模型中，买和卖可能横跨2到4个交易日。所以可以暂时不考虑日内振幅对收益的正影响，而专注于振幅对收益的负影响。

但是，忽略股票市场波动对收益的影响是否安全呢？舒维特（Schwert）考察了19世纪中叶到20世纪80年代的美国证券市场[21]，发现股市波动并不完全按照各种宏观经济指标的波动幅度而波动，只有微弱证据能支持经济波动可以用来预测股票波动，同时股票市场更加受到金融杠杆的影响（如利率等），而市场交易行为直接影响股市波动，比如当月交易日多的话，股市波动就更大。舒维特着重关注了大萧条（Great Depression）时期，发现股市波动并没有预想的那样激烈，他认为这是由于对未来的不确定性导致股市交易变得更谨慎。所以，在大萧条这样悲观下行的基本面下，股市的波动却并没有按照同样剧烈幅度而波动。汉密尔顿站在经济周期的视角上，对战后到20世纪90年代的股票市场进行分析也得出了类似的结论[22]。因此，我们可以假设股市的波动同时受到经济周期和投资行为（风格）的影响。针对不同股票市场波动情况的差异，可以用不同国家在经济周期中位置的不同来解释，也可以用市场交易的风格来解释。其中，即使处于经济周期中衰退的时段，股票市场也并不一定随着一样的比例而波动。所以不同股票市场的波动可以认为是相对独立的，因此在分析比较不同市场预测效率时，可以把波动元素进行合适处理。

再回到表2中两组指数，直观地看，振幅对预测误差有明显的正向作用，即振幅越大，誤差就越大。如果对两组指数，分别把其中各个指标额度平均预测误差求和后再除以其相应的振幅，这样得到的结果我们称之为相对稳定度。计算后，上证指数的相对稳定度是3.14，纳斯达克指数是3.33。即在同样的振幅下，纳斯达克指数相与上证指数预测难度是基本相同的。

从套利空间来看，从收益着手建立表3。因为模拟交易并不需要预测开盘和收盘，故排除开盘收盘的预测误差。最高价、最低价的平均相对误差统计见图4与图5。考虑到上面论证的振幅对收益的负作用，我们可以把平均振幅作为补偿项，然后乘以收益。可以看到，上证指数经过调整后，上证指数的收益要大于纳斯达克指数。同样，收益乘以误差补偿项也可以用来做参考，上述两种调整后的值都可以称作相对套利空间。最后需要注意的是，上证指数的交易日和实际交易次数都要小于纳斯达克指数，所以整体的套利空间还要更大，这对于上证市场的成熟度不如纳斯达克市场这一推论，也是一个值得关注的佐证。

对于证券市场稳定性的整体评估应该以绝对稳定性为主要观测指标，因为其能观察、评估市场运行的平稳度，即价格的波动性;而把相对稳定度作为次要观测指标，是因为其剔除了平均振幅对预测误差的影响;VaP考察的是市场的成熟程度，可以作为次要参考指标。

五、小结

本文在金融安全的背景下，考察了我国证券市场是否运行稳定，选取了上证指数作为研究对象，以及纳斯达克综合指数作为参照对比。使用支持向量机作为预测工具，对上述指数使用窗口滑动法进行预测，并得到价格的预测数据，结果表明：（1）上证指数整体的稳定度是大于纳斯达克指数的（绝对预测误差较大），这说明我国股市整体波动不容易预估，而随之而来的风险也更大;（2）在考虑到上证指数平均振幅大于美指的情况下，我们对预测误差进行了处理，得到两个市场的相对稳定度大体相等的结果;（3）通过套利空间分析，上证指数的套利价值要大于纳斯达克指数，说明总体上我国证券市场没有美国股市成熟。最后，在金融安全的大背景下，对于证券市场稳定的判断应该以绝对稳定度为主要参考指标，相对稳定度和套利价值则作为次要参考指标。

上述结论不仅对于投资者，而且对决策者同样有参考价值。本文基于成熟市场的行为模式，通过对比中国股市和发达、成熟的美国市场，对两个市场稳定性进行数值上的比较。后续研究可以加入多个其他市场（周边的市场，如韩国，或其他新兴经济体的证券市场）进行对比分析，可能对我国证券市场安全稳定有更深入的理解。通过在数值上对比不同市场的稳定度和成熟度，对于决策者，可以作为何时推进后续管理政策或推进节奏的参考与佐证。

最后，从试验方法上看，虽然SVM预测效果比较良好，后续研究可以加入遗传算法，使得SVM的参数的选择在时序上更为动态进而能提升整体的预测效率。针对VaP，后续可对其模拟规则予以丰富、完善，使其更加接近套利者的投资思路或状态。

注释：

①  左纵轴单位是亿元人民币，右边则是十亿美元。数据来源：国泰安数据库，圣路易斯联邦储蓄银行。

② 左纵轴是上证指数的标度，右边是纳斯达克综合指数。上证指数数据来源为国泰安数据库，纳斯达克综合指数数据采集自雅虎财经。

参考文献：

[1]Fama E F. Efficient capital markets： a review of theory and empirical work[J]. Journal of Finance， 1970，25（2）， 383417.

[2]Hamilton J D. A new approach to the economic analysis of nonstationary time series and the business cycle[J]. Econometrica， 1989，57（2）， 357384.

[3]Rotemberg J J. Prices， output， and hours： an empirical analysis based on a sticky price model[J]. Journal of Monetary Economics，1996，37（3）， 505533.

[4]刘海玥、白艳萍.时间序列模型和神经网络模型在股票预测中的分析[J].数学的实践与认识，2011（4）：1419.

[5]Kim K J， Han I. Genetic algorithms approach to feature discretization in artificial neural networks for the prediction of stock price index[J]. Expert Systems with Applications，2000，19（2）， 125132.

[6]Kim K J. Financial time series forecasting using support vector machines[J]. Neurocomputing， 2003，55（12）：307319.

[7]Quah T S， Srinivasan B. Improving returns on stock investment through neural network selection[J]. Expert Systems with Applications ，1999，17（4）， 295301.

[8]苏治， 方明， 李志刚.STAR与ANN模型：证券价格非线性动态特征及可预测性研究[J].中国管理科学，2008（5）：916.

[9]黄少荣.粒子群优化算法综述[J].计算机工程与设计，2009（8）：19771980.

[10]沈艳，郭兵，古天祥.粒子群优化算法及其与遗传算法的比较[J].电子科技大学学报，2005（5）：696699.

[11]Hassan M R， Nath B. StockMarket Forecasting Using Hidden Markov Model： A New Approach// International Conference on Intelligent Systems Design and Applications[EB/OL]. Isda '05. Proceedings. IEEE， 2005：192196.

[12]Hassan M R， Nath B， Kirley M. A fusion model of HMM， ANN and GA for stock market forecasting[M]. Pergamon Press， Inc，2007.

[13]李杰，王建中，胡紅萍.基于PCA的BP神经网络股票预测研究[J].太原师范学院学报（自然科学版），2011（3）：6063.

[14]蔡红， 陈荣耀.基于PCABP神经网络的股票价格预测研究[J].计算机仿真，2011（3）：365368.

[15]Tsai C F， Hsiao Y C. Combining multiple feature selection methods for stock prediction： Union， intersection， and multiintersection approaches[J]. Decision Support Systems，2011，50（1）：258269.

[16]Lopez J A. Regulatory evaluation of valueatrisk model[J]. Social Science Electronic Publishing，1997，（1）：3764.

[17]Vapnik V N. An overview of statistical learning theory[J]. IEEE Transactions on Neural Networks，1999，10（5）：98899.

[18]刘志亭，张慧云.上证180指数“周末效应”的实证分析[J].青岛科技大学学报（自然科学版），2006（4）：359362.

[19]陆江川，陈军.基于DellavignaPollet模型的我国股票市场PEAD现象周历效应——以深圳主板市场为证据[J].系统工程，2011（7）：2633.

[20]Leigh W， Modani N， Hightower R. A computational implementation of stock charting： abrupt volume increase as signal for movement in New York Stock Exchange Composite Index[J]. Decision Support Systems，2004，37（4）：515530.

[21]Schwert G W. Why does stock market volatility change over time[J]. Journal of Finance，1989，44（5）， 11151153.

[22]Hamilton J D， Lin G. Stock market volatility and the business cycle[J]. Journal of Applied Econometrics，1996，11（5）：573593.

（责任编辑：铁青）