基于模糊层次综合分析法对隧道施工常见风险的分析
2019-03-06赵轩
赵 轩
(陕西省土地工程建设集团渭北分公司,陕西 咸阳 712000)
0 引 言
我国幅员辽阔,交通建设任务复杂繁重。近年来,随着经济的良好快速发展,隧道建设也在大规模进行之中。由于地质环境、设计指标和人为因素的多种影响,在工程施工及运营过程中不断面临着多种风险,导致较大的人员伤亡和经济损失。因此,开展风险分析评价是避灾减灾的必要手段,对确保工程建设顺利进行并减少国民经济损失具有重要的意义。本文通过广泛收集整理公路隧道施工时期产生的风险情况,对某隧道施工过程中风险进行计算分析,为工程施工建设提供指导及参考依据。
1 风险识别内容
为了较为全面体现出隧道施工建设过程中发生风险的因素,方便隶属度的确定,本文将 40 余次风险发生的统计数据按照等级划分,依次是:围岩级别、开挖面积、埋深、偏压、地下水、不良地质构造、地应力及施工单位综合技术水平情况[1]。等级越高,风险度就越大,风险发生的概率也就越大,并将各影响因素进一步进行了详细等级划分[2-4]。
2 构建风险分析模型
2.1 模糊综合评价法
模糊综合评价在多种因素影响下的全面评价过程中十分有效[5]。模糊综合评价依据既定的评价标准、评价因素的实测值,确定各因素对评价目标的影响力大小,即权值集,然后进行单因素评价得到各单因素的模糊关系矩阵。经过变换后,得到对事物作出评价的评判集,如式(1)所示。

式中:B={B1,B2,…,Bn},Bn为评价对象第 n 评价级别的隶属度,ω 为权值集,r 为各单因素模糊关系矩阵。最后,根据最大隶属度原则,确定目标最终发生概率及程度[6]。
典型隶属度函数有三角函数分布、梯形分布、抛物型分布、正态分布和 Cauchy 型分布,如表1 所示。
对围岩级别,地质构造偏压、不良地质构造、地下水、施工单位技术和管理水平 5 个不便分级的因素,采用 Kaiwowski 等人提出的模糊隶属度评价矩阵进行分级。
2.2 确定各因素权重
本文拟采用层次分析法[7]计算隧道施工建设中风险因素权值集ω。运用 AHP 进行分析时,分以下 4 个步骤。
1)分析系统中各因素之间关系,建立问题的递阶层次结构。
2)对同一层次的各元素关于上一层中某一准则的重要性进行两两比较,构造两两比较判断矩阵。判断矩阵中元素 aij具有如下性质:aij>0,aij=1/aji;aii=1。在确定完判断矩阵后,先计算判断矩阵的最大特征根 λmax和其对应的特征向量,然后进行判断矩阵的一致性检验。一致性指标如式(2)所示。

式中:n 为阶数。
一致性比例计算方式如式(3)所示。

表1 开挖面积、埋深和地应力因素发生概率隶属度函数

式中:RI为平均随机指标,是多次(500 次以上)重复进行随机判断矩阵特征值的计算后取算数平均值。
当 CR<0.1 时,认为矩阵是满足一致性要求的。此时对 λmax对应的特征向量进行归一化处理得到判断矩阵的权重值。
3)由判断矩阵计算被比较元素相对权重。
4)计算各层元素的组合权重,并进行排序。
3 隧道施工中围岩变形风险分析
本节以某隧道工程为例,对施工中发生大变形风险进行估计。
该工程段断面位于 Fd2 断层破碎带中,围岩物质组成为构造片岩、局部夹断层泥化带,岩体破碎呈碎裂状以及散体状结构。围岩级别确定为Ⅴ级弱围岩。地下水以淋雨状为主,在雨季将以股状出水为主,在靠近上、下断层上、下盘会出现较大的涌水现象。
3.1 建立因素集
本文预测的案例工程段围岩级别为Ⅴ级、开挖断面面积 121 m2、最大埋深 130 m、处于断层带中、地下水富集、开挖后主要以淋雨状出水为主、无偏压、地应力无影响。Fd2 断层破碎带岩体极为破碎,片理极其发育,按不良地质影响严重对待。施工单位技术和管理因素按较丰富、技术力量雄厚对待。该工程段断面大变形风险因素如表2 所示。此外,因素集参照风险识别的因素及相同等级划分。
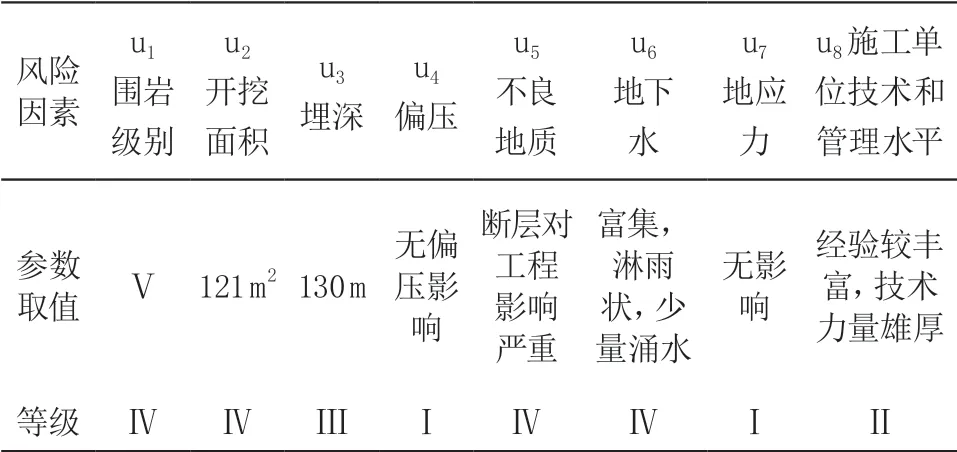
表2 某断面隧道大变形风险因素对照表
3.2 建立评价集
隧道大变形一般以变形量来衡量,由变形量对变形进行等级划分,并用模糊语言建立的评价集T={t1,t2,t3,t4,t5},如表3 所示。

表3 大变形等级划分及结果评价
3.3 确定隶属度 建立后果评价矩阵
通过分析 40 余个隧道施工常见风险的统计资料,对开挖断面面积与不同等级变形的发生次数进行统计,采用统计法得出开挖断面面积的隶属度,对由于资料不完整和不易量化的因素,采用 Karwowski 提出的隶属度矩阵来判断。
通过确定了该隧道大变形的风险因素,对风险因素等级进行了划分,通过查询表1 中的隧道大变形隶属度函数和因素发生概率等级评价矩阵,根据风险评估计算模型,得到风险评价矩阵 R1、R2。

3.4 确定权重
由隧道大变形风险调查表的频数统计,得各因素在 42 次大变形中每项的出现次数,得到出现频率,再将频率归一化,得到客观权重 Ak,如式(4)所示。
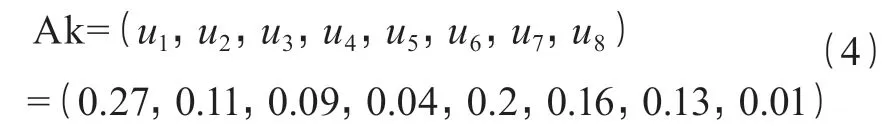
式中:u1~8分别代表围岩级别、开挖面积、埋深、偏压、地下水、不良地质构造、地应力及施工单位综合技术水平对应的客观权重值。
通过 MATLAB 计算出判断矩阵的最大特征值和特征向量,检验判断矩阵的一致性。

因此,判断矩阵一致性可以接受。
将最大特征值对应的特征向量归一化,即得到各因素权重集。
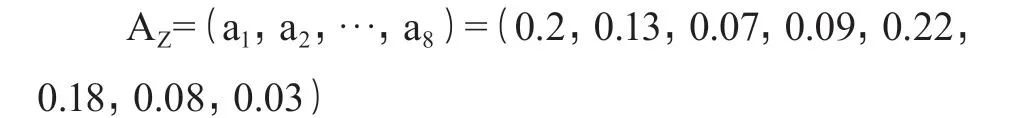
参考专家[4]取 k1=0.3,k2=0.7。

发生概率模糊评价:
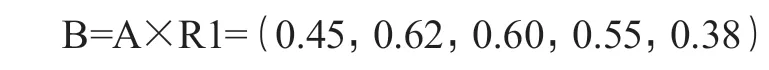
发生后果模糊评价:
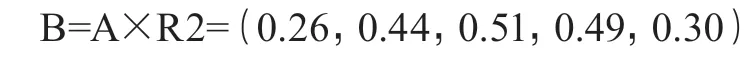
3.5 评价结果
根据最大隶属度原则,该项目隧道 K15+544 处发生大变形风险的概率等级是可能(Ⅱ级),发生后果是严重(Ⅲ级)和非常严重(Ⅳ级)。
根据现场实际情况,该项目隧道 K15+544 处在 5 月 15 日、5 月 17 日和 6 月 5 日发生了三次大变形,并伴随涌水和坍塌现象。最大变形量达到 900 mm,可见评价结论与现场结果基本相符,证明了本文建立的模型的适用和准确性。
4 结 论
本文通过建立模糊层次综合分析模型,针对隧道施工常见风险展开分析。通过广泛收集整理隧道施工常见风险案例资料,结合综合赋权法,将专家意见与客观统计资料相结合,得出最终权重,并验证了模型的适用性和准确性。本文结论有以下几点。
1)隧道施工中发生大变形的成因主要为地质水文条件及设计断面参数,通过模糊数学的案例分析与专家经验结合,可有效辨识风险形成的因素,并确定其权重。通过计算评价,为隧道施工中大变形风险评估提供了依据与参考。
2)建立模糊层次综合分析模型,可有效地判断、预测隧道施工中大变形风险,并可拓展用于类似风险分析中。
3)隧道大变形风险影响因素较为复杂,宜采用定性与定量结合的方法量化其影响程度。对可量化的因子采用隶属度函数进行划分,但定性分析的因子仍需进一步细化其影响程度。
