短波中标称伴流场特性分析
2019-03-06郭春雨赵庆新郝浩浩
郭春雨, 刘 恬, 赵庆新, 郝浩浩
(1. 哈尔滨工程大学 船舶工程学院, 哈尔滨 150001; 2. 哈尔滨工业大学 能源科学与工程学院, 哈尔滨 150001)
船舶在运动过程中,船体周围伴随着一股水流,称为伴流或迹流.根据其成因,可分为摩擦伴流、形势伴流和波浪伴流[1].对于船舶在实际海况下的快速性来说,船舶在风浪中的运营能效对船舶设计具有重要意义,而船尾桨盘面处轴向标称伴流场对螺旋桨设计至关重要,长久以来,研究者们对伴流场的研究较多地集中于时均下的标称伴流场、平均伴流分数及尺度效应的研究[2].第26届ITTC伴流场尺度效应换算专家委员会对已有的换算方法进行了总结[3],其中Sasajima[4]假设伴流由摩擦伴流、波浪伴流和形势伴流线性叠加而成,忽略自由液面效应对伴流场的影响,不考虑形势伴流的尺度效应,对摩擦伴流分数进行摩擦阻力系数的修正得到实尺度的伴流分数.利用Sasajima所提方法或其他方法对时均下桨盘面上的平均伴流分数进行修正虽然存在一些问题,但是已经得到了广泛的应用.
对于实际海况下的实船伴流场来说,除了受到由于雷诺数不相似造成的尺度效应的影响外,还会受到波浪的影响.长久以来,在尺度效应换算或者伴流场计算中,都会忽略波浪伴流分数的影响.但是,也有很多研究者研究了波浪条件下船尾流场的变化.Weymouth等[5]利用软件CFDSHIP-IOWA对Wigley船型在规则波海况中不同的弗劳德数、波长、波幅条件下的纵摇和垂荡运动进行预报,同时对自由表面和边界层进行研究.结果表明,RANS方法在对船舶小幅度运动、附加质量系数和流场的预报等方面具有很高的精度.Simonsen等[6]利用CFDSHIP-IOWA对KCS船型在规则波顶浪航行过程中共振状态下的垂荡和纵摇运动幅值及波浪增阻进行预报.Sadat-Hosseini等[7]利用CFDSHIP-IOWAv4.5程序对KVLCC2船型在迎浪短波和长波工况下的波浪增阻和运动响应进行了数值计算(CFD)的验证与确认,文中对长波工况下考虑船舶运动响应的船身边界层在一个波浪周期内的变化进行了相关分析,并对典型时刻下螺旋桨桨盘面所在尾流伴流场,与相应时刻下粒子图像测速法(PIV)测量结果进行了对比验证.吴乘胜等[8]采用基于RANS方法的数值造波技术,对KCS船模在规则短波中顶浪航行时尾伴流场特性进行研究,分析波浪对平均伴流分数的影响,比较了伴流场不同时刻下的速度分布的不同.结果表明, 当波浪存在时,平均轴向伴流分数呈减小趋势,并提出了伴流分数较小的主要原因是波浪的质量迁移现象.
在国内外学者研究工作的基础上,本文使用CFD方法对规则短波顶浪航行下KCS船模的约束模型进行数值计算,采用约束模型的主要原因是由于船舶在实际海况下航行时,遭遇的通常为短波(相对船长),而短波对船舶6自由度运动影响相对长波较小,因此忽略船模姿态变化,并可以为探讨船舶在波浪条件6自由度运动状态下的伴流场特征变化提供约束模型下的对比分析数据.因此,本文主要分析波浪对平均伴流分数、标称伴流场和伴流峰值的影响.这对研究波浪与静水条件下伴流场的差异具有一定意义.
1 数值模型
1.1 控制方程
不可压缩牛顿流体的运动满足连续性方程和动量守恒方程[9]:
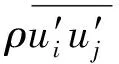
1.2 研究对象
采用国际船舶CFD会议中提供的标准船型KCS的标准模型之一进行静水及波浪条件下的数值计算.KRISO曾对KCS船模在拖曳水池中进行了一系列试验,静水下有详细的阻力、伴流场和自由表面兴波等数据[10].几何模型如图1所示.
船模与实船的弗劳德数相等(Fr=0.26),计算不考虑船舶姿态变化.模型尺度与实尺度的KCS船型参数对比如表1所示.

图1 KCS几何模型Fig.1 KCS geometric model
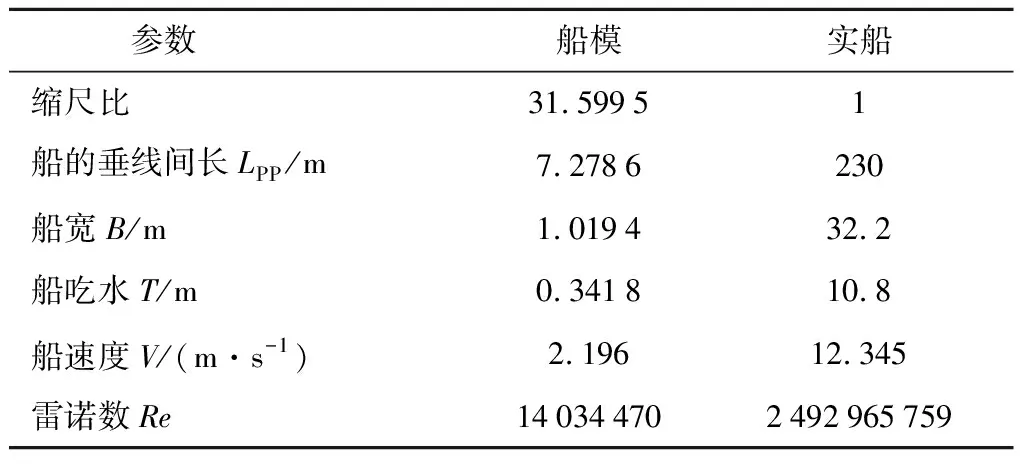
表1 KCS船模主要参数Tab.1 Model parameters of KCS
1.3 计算工况描述
表2给出了静水以及波浪中的计算工况,选取的6种工况皆为短波工况,主要原因是船舶在顶浪航行遭遇短波时,船舶的纵摇运动相对而言较为缓和[1].因此,本文忽略了纵摇和垂荡作用,船舶姿态为固定姿态.
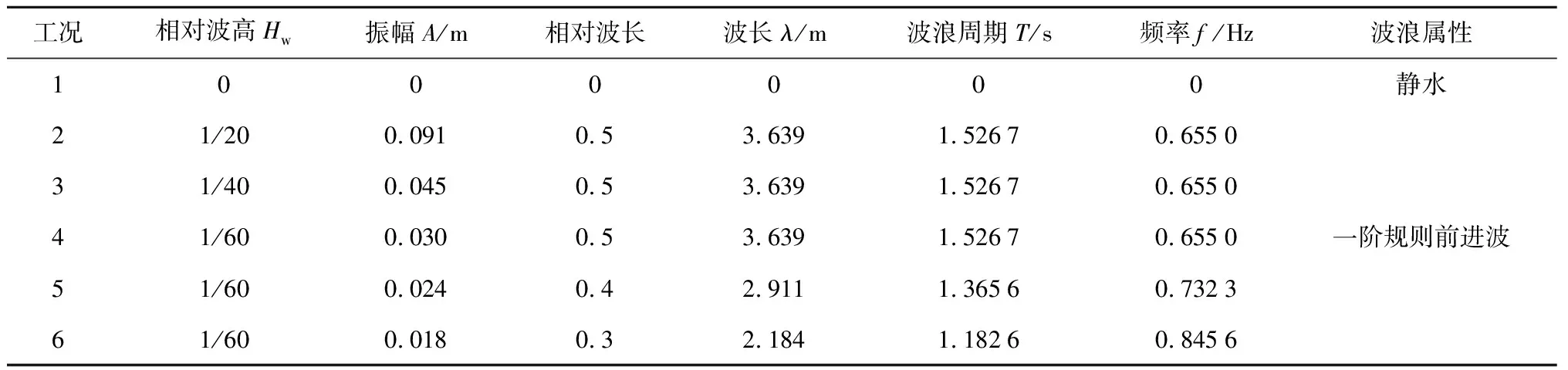
表2 静水及波浪中的计算工况Tab.2 Computational parameters in calm water and in wave
1.4 边界条件及网格划分
以船体中线面上艉柱与基线的交点为原点,计算域的范围取-1.0Lpp≤x≤3.0Lpp,0≤y≤1.0Lpp,-2.0Lpp≤z≤1.0Lpp(其中:x为沿船长方向;y为沿船宽方向;z为沿高度方向),在数值波浪水池的模拟中,采用速度入口条件,模拟波浪场流体的速度分布来产生一阶规则入射波,波面方程为
η=Acos(kx-ωt)
其中:k为波数;ω为圆频率;t为物理时间.造波速度边界为
(3)
式中:U0为流体入口速度.在距Outlet 3倍波长λ范围内设置为阻尼消波区,具体边界条件设置如表3所示.计算域如图2所示.
网格划分采取Star-CCM+中的网格划分工具划分切割体网格(Trimmed Mesh)和边界层(Prism Layer Mesh),边界层厚度为20 mm,边界层数为8层,具体网格参数如表4所示.除了对船首和船尾进行一定的加密,为了保证波浪模拟的精度,需要在单个波高波长的范围内设置不少于一定数目的网格.

表3 边界条件Tab.3 Boundary conditions
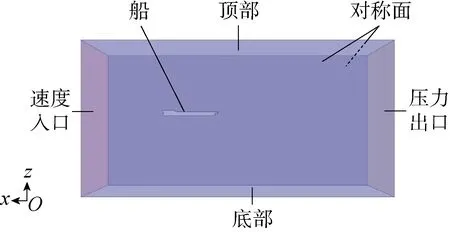
图2 计算域示意图Fig.2 Diagram of computational domain
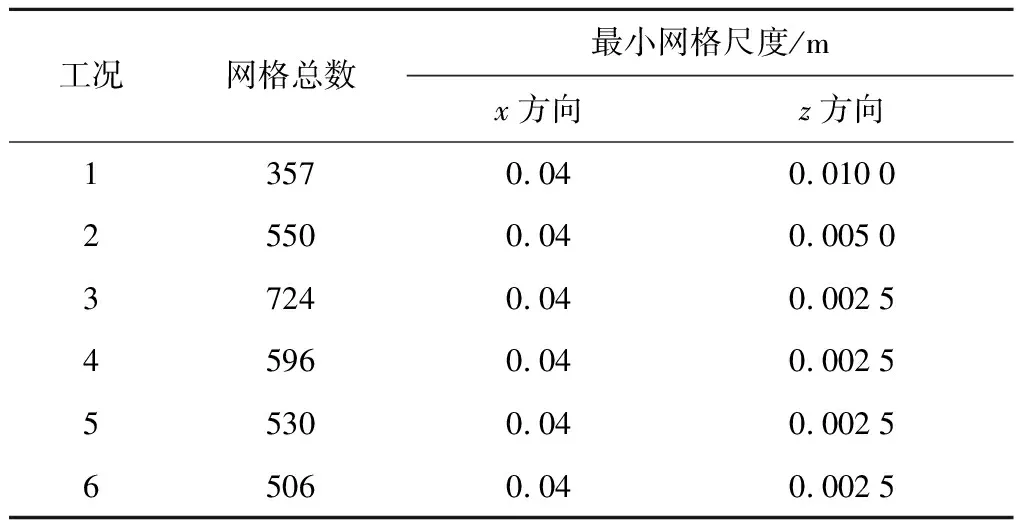
表4 网格参数Tab.4 Mesh parameters
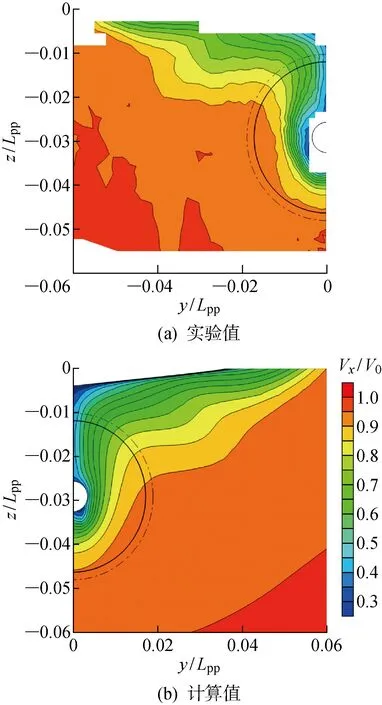
图3 桨盘面处无量纲轴向速度实验值与计算值对比Fig.3 Comparison of non-dimensional axial velocity field at propeller plane
2 计算结果与分析
2.1 静水下计算结果验证
通过上述数值模型对静水中船模进行计算,所得总阻力系数Ct=3.308×10-3,相比于实验值[10]3.557×10-3,误差约为7%,在可接受范围内.图3所示为静水下KCS船模(Lpp=7.278 6 m)桨盘面处无量纲轴向速度实验值与计算值对比.图中:实验值来自于Kim等[10]在2001年发布的实验结果;Vx为伴流的轴向速度;V0为与船速相同的流场进速.可以看出,轴向伴流场的速度分布梯度和范围等都较为一致,数值误差相对较小,满足计算精度要求,可以利用该数值模型的计算结果进行分析.
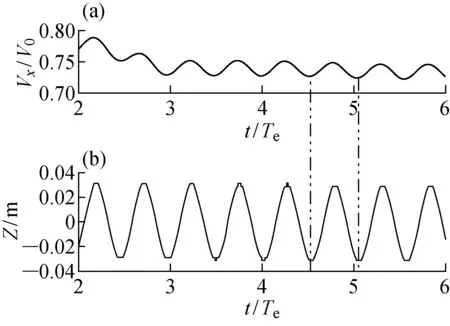
图4 平均伴流分数和入射波高时历曲线Fig.4 Time history of average wake fraction and incident wave height
2.2 波浪工况下计算结果
图4(a)所示为工况4的桨盘面处轴向速度时历曲线,并且在距桨盘面4倍波长处,设置波高仪,得到波高仪时历曲线如图4(b)所示.图中:t/Te为无因次时间;Vx/V0为无因次轴向速度;Z为入射波波高.对于规则波顶浪航行状态下的船尾标称伴流分数时历曲线来说,满足与入射波浪近似相同的周期性变化规律,两者之间的峰值、谷值对应无因次时间基本相同,但峰值与谷值之间存在一定偏差.造成这种现象的主要原因是,数值波浪水池在波浪传播过程中,由于数值耗散,产生了一定的波浪衰减,使两者之间存在偏差.
3 波浪参数变化对伴流场影响
3.1 波高参数对伴流场影响分析
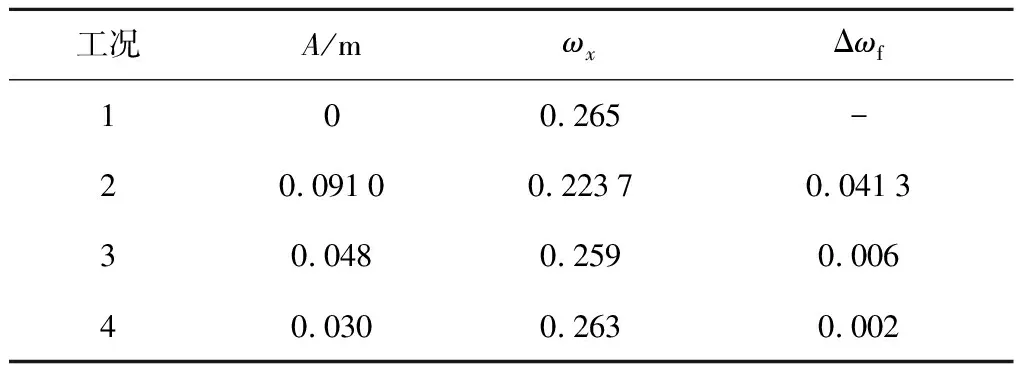
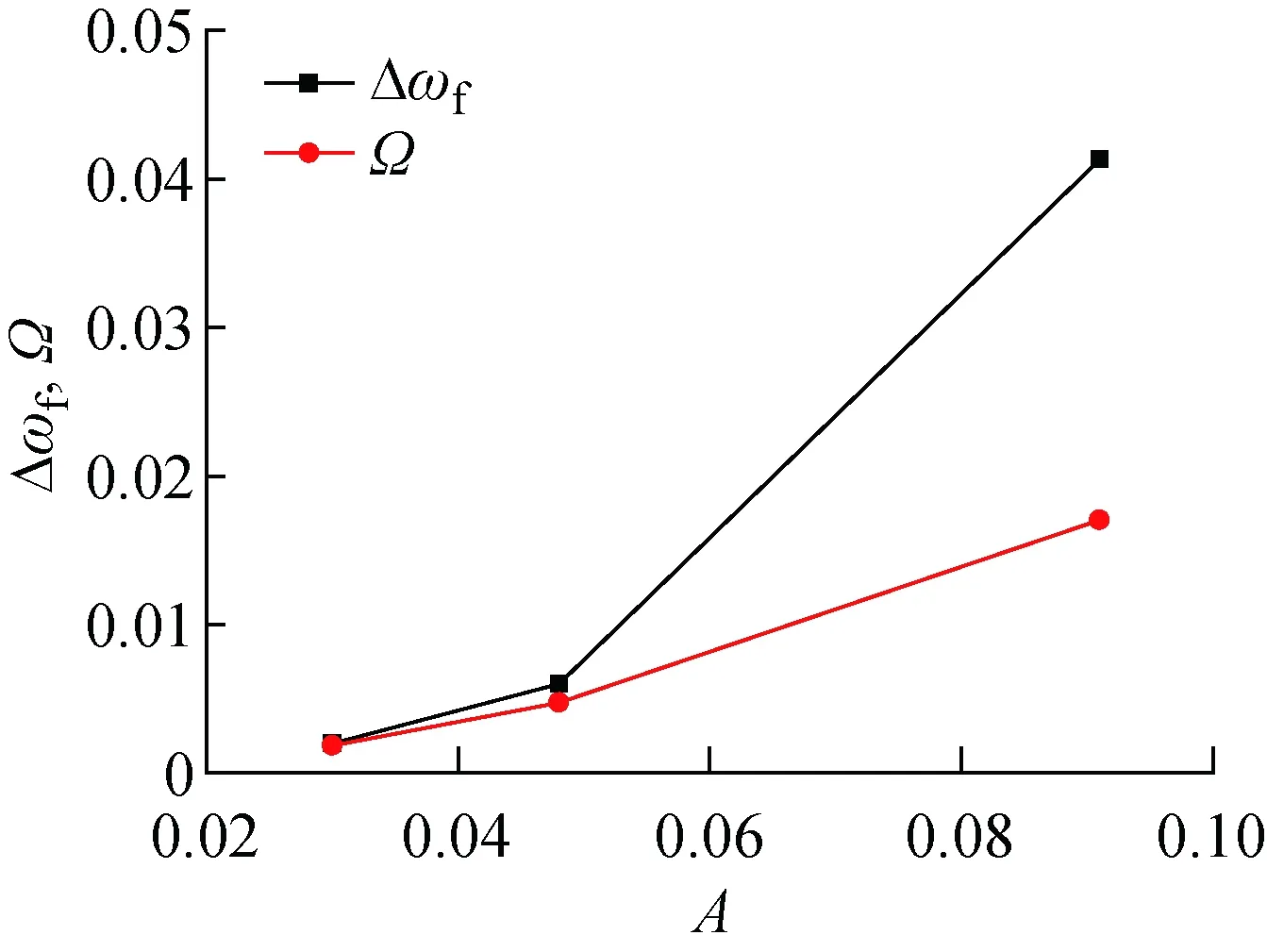
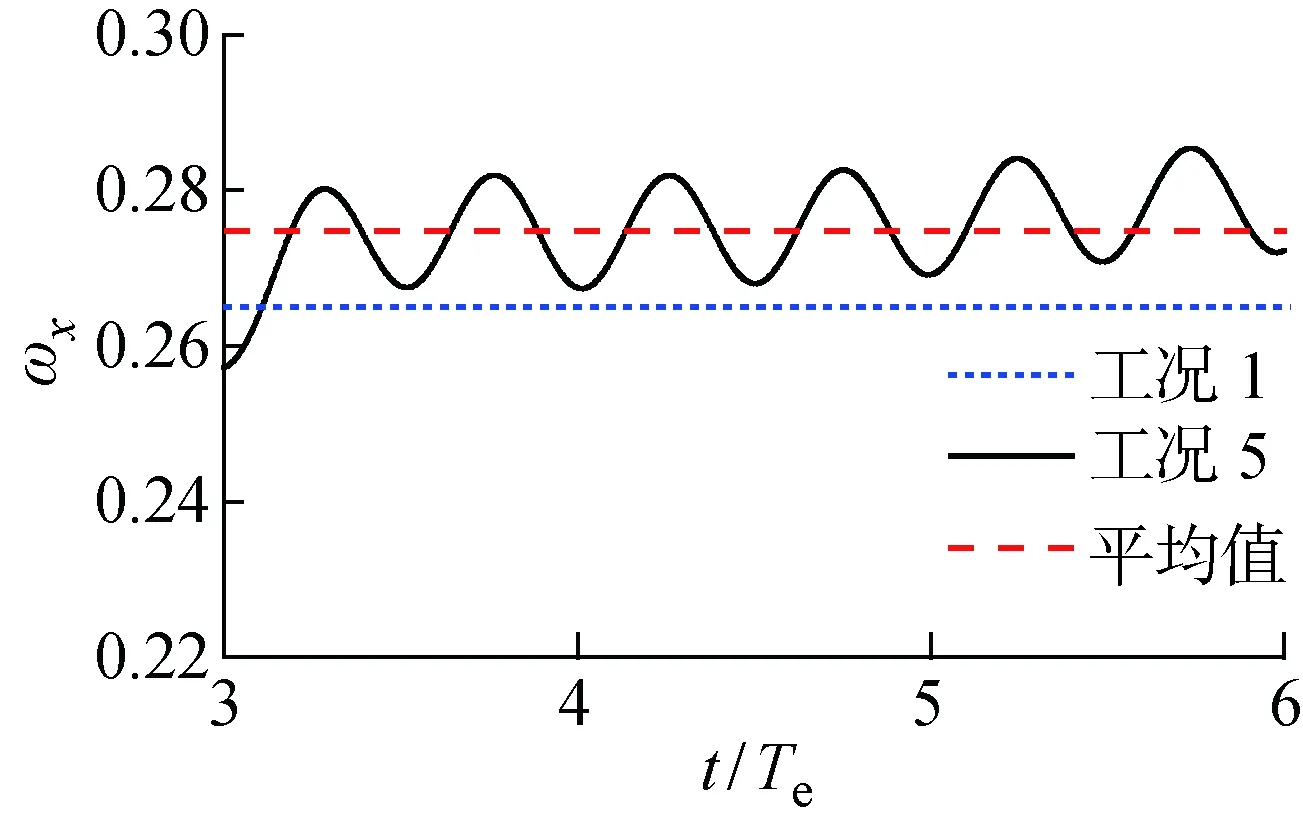
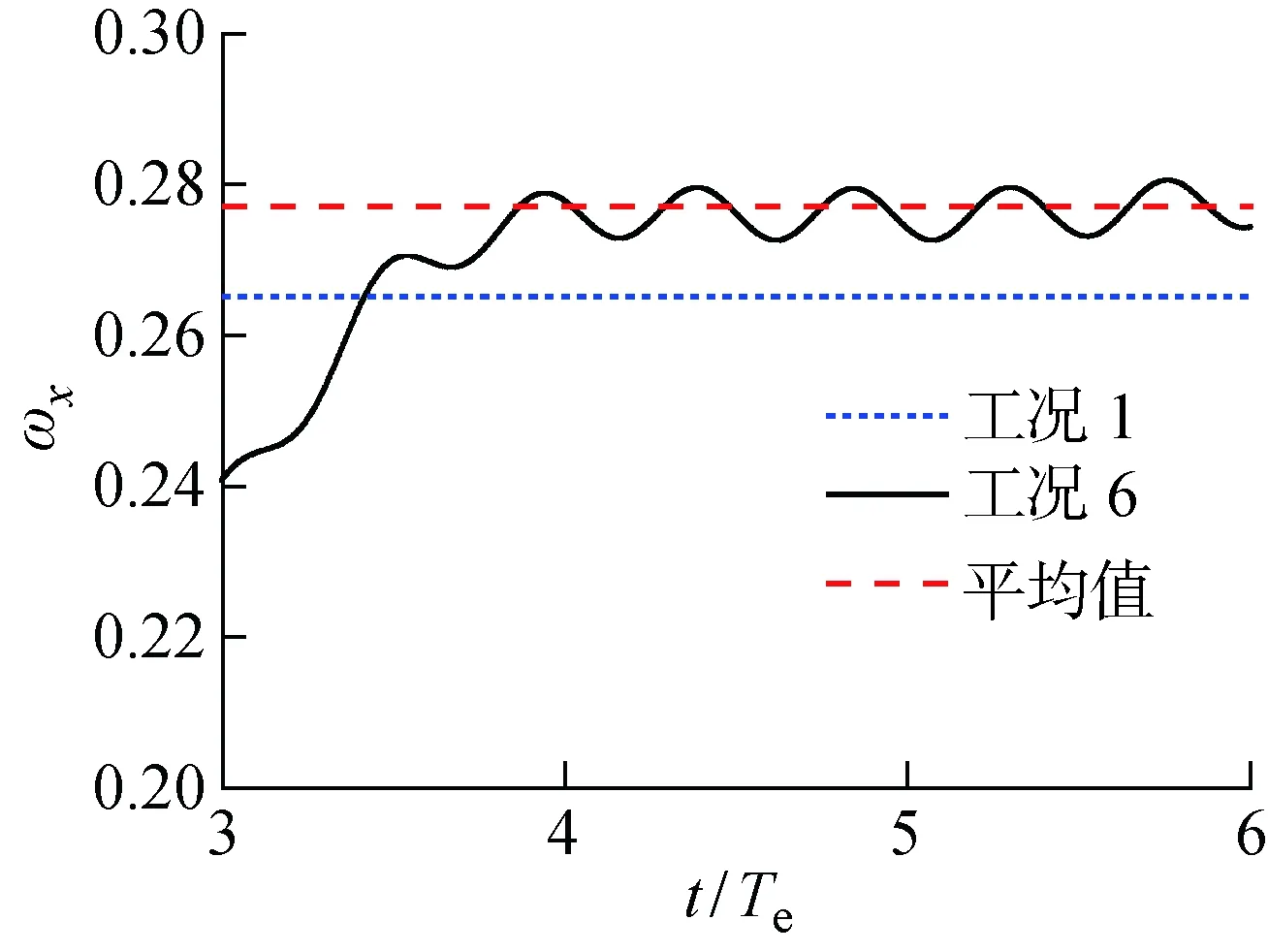
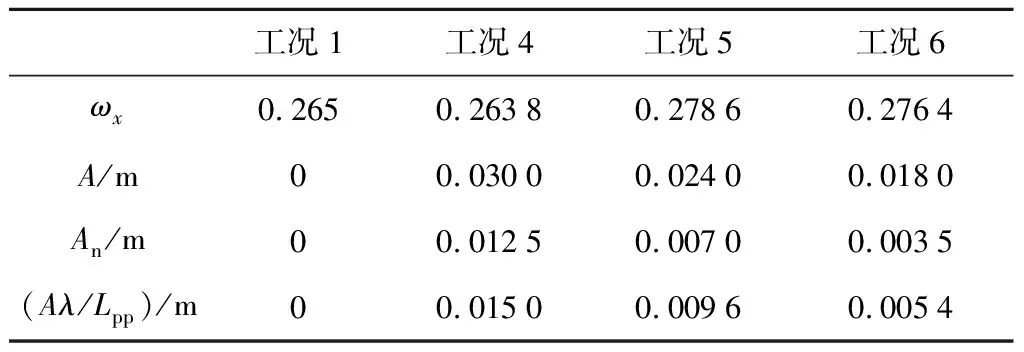
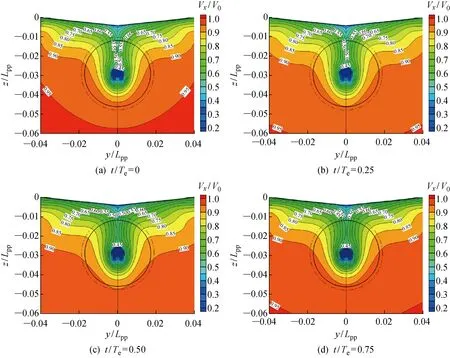
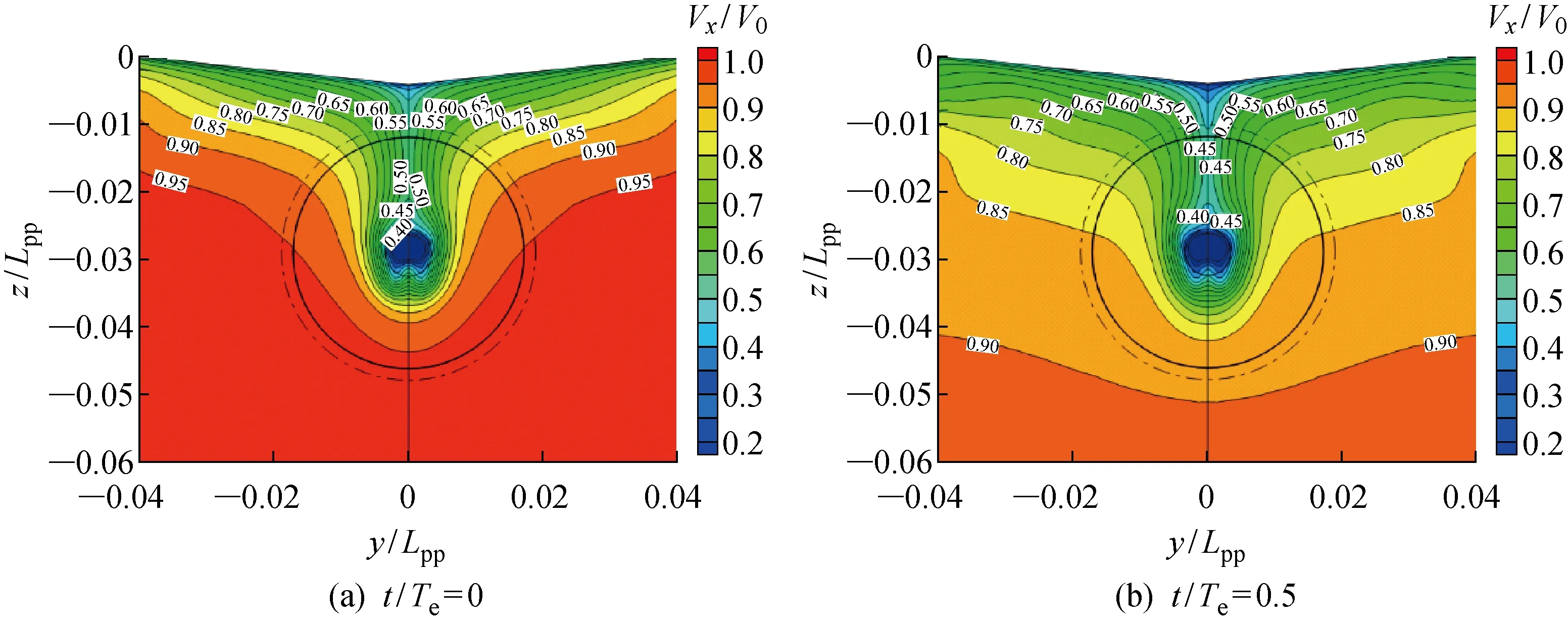
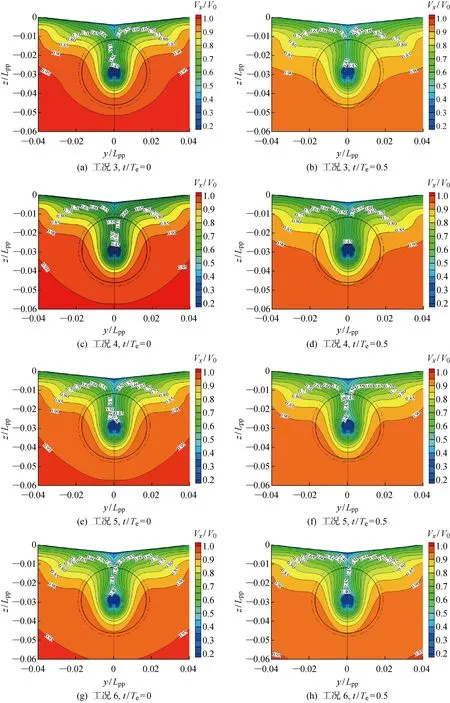
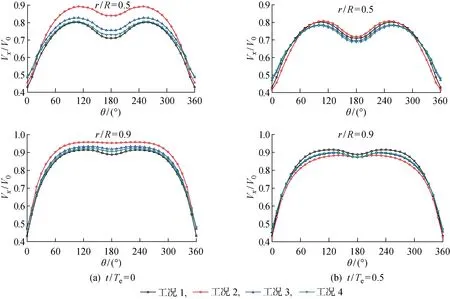
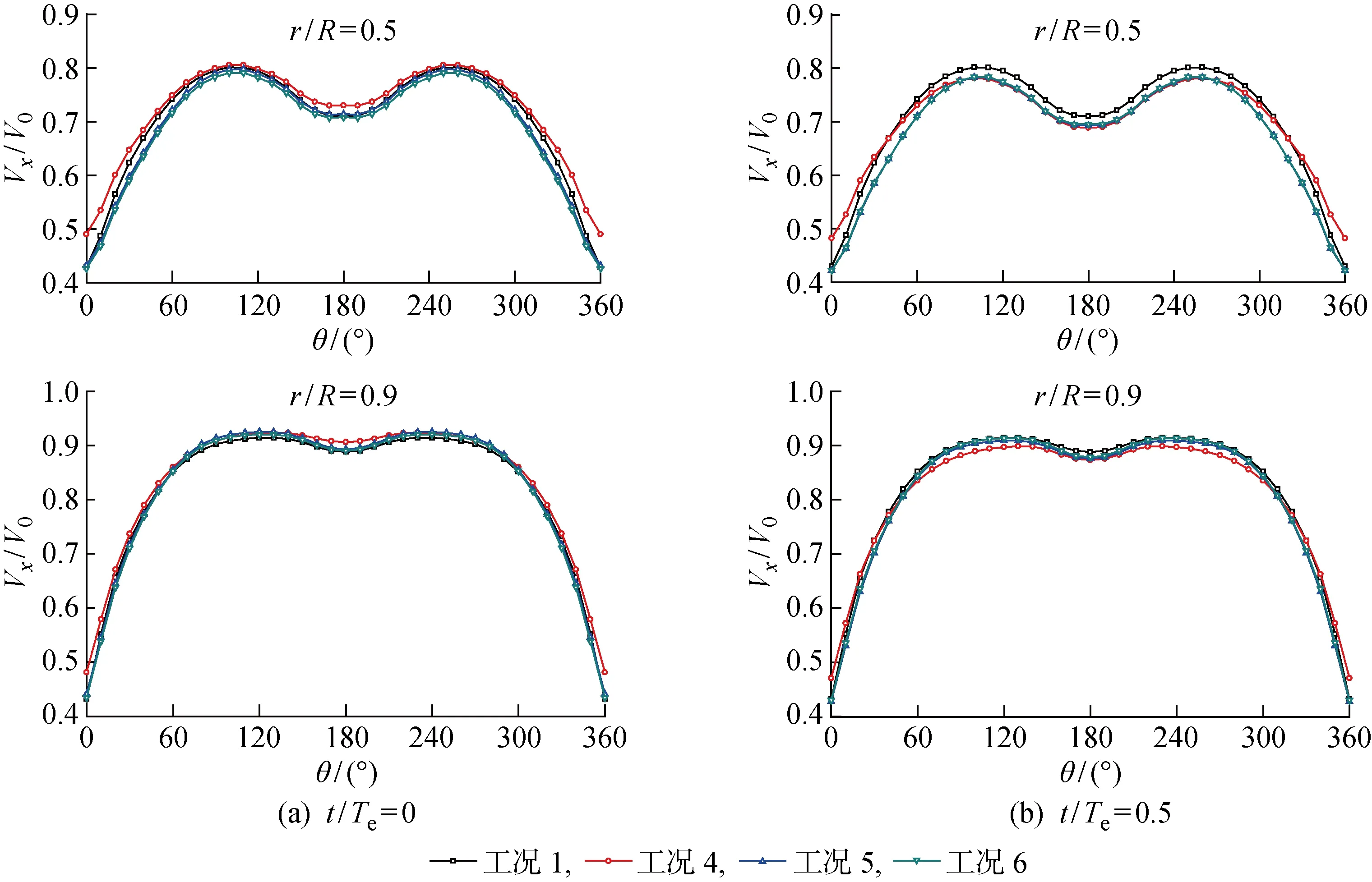
对工况2、3和4计算结果进行对比,分析不同波高条件下对伴流分数的影响,结果如图5所示.由图可以看出,波高对伴流分数的影响作用明显,波浪中水质点的轨圆运动使伴流分数呈现与波浪及水质点运动周期相同的运动,并且伴流分数曲线振幅与入射波浪振幅呈现正相关关系,即波浪振幅越大,伴流分数震荡越剧烈.同时,桨盘面上伴流分数的峰值随振幅增大变化不明显,而伴流分数谷值变化明显.这主要是由于流体质点做轨圆运动时,迹线不闭合,会发生在波浪传播方向的波漂流(Stokes Drift Current)[11],对垂向方向上,区间-∞ Ω=ωA2/2 (4) 由此可见:随着Hw的增大,ω不变,总平均漂移流量Ω增大,对应轴向平均伴流分数ωx变小;随着A增大,伴流分数振幅Aw变大,将会造成明显的波峰不变和波谷明显变小的特点. 图5 随波高变化的轴向伴流分数时历曲线Fig.5 Time history of average wake fraction and incident wave height 表5所示为桨盘面上轴向伴流分数随波高变化.表中:Δωf为带波浪工况下与静水中的轴向伴流分数ωx之差.由表可见,与静水条件下桨盘面处轴向标称伴流分数相比,波长相同时,波浪振幅越大,单一周期下平均伴流分数减小越明显,即波浪伴流分数的绝对值越大.但是,对于工况3和4,即波陡较小时,波浪伴流分数占比很小,这也十分符合研究者们得出的波浪伴流分数很小,可以忽略的结论[1]. 表5桨盘面上轴向伴流分数随波高变化 Tab.5Axialwakefractioninpropellerdiskwithvariationofwaveheight 工况A/mωxΔωf100.265-20.09100.22370.041330.0480.2590.00640.0300.2630.002 由图6可知,在入射波浪振幅A较小时,波浪伴流分数绝对值与总平均漂移量Ω近似相似,当波浪振幅A增大后,桨盘面上的波浪伴流分数绝对值远大于区间-∞ 图6 伴流分数变化量与总平均漂移量对比Fig.6 Comparison of variation of wake fraction and the average total drift 波浪波长的变化会造成流体质点运动的周期不一致,并随λ减小,ω增大,当波陡Hw/λ=1/60不变时,振幅随波长减小而减小,对于二阶Ω,Ω∝λ3/2.可见,随着波长的减小,总平均漂移量呈指数减小.但是,由图6可知,当Hw/λ=1/60和λ/Lpp=0.5 时,总平均漂移量占比已经很小,当波长再减小时,总平均漂移量对伴流场的影响基本可忽略不计. 由图7和图8可知,在相对波陡不变的情况下,随着波长和振幅的减小,伴流分数不再减小并相对增大.可见,当二阶Ω较小即可忽略时,由于船尾流场的复杂变化,伴流场不再满足平均伴流分数减小的趋势,反而略大于静水.取多个周期下振幅的平均值An,如表6所示.可以看出,平均伴流分数时历曲线的振幅An也随着波浪振幅A的减小而迅速减小,并且该减小量与波长船长比λ/Lpp密切相关.由表6的对比可知,An与Aλ/Lpp十分接近. 图7 工况5的轴向伴流分数时历曲线Fig.7 Time history of axial wake fraction in Condition 5 图8 工况6的轴向伴流分数时历曲线Fig.8 Time history of axial wake fraction in Condition 6 表6桨盘面上轴向伴流分数随波长变化 Tab.6Axialwakefractioninpropellerdiskwithvariationofwavelength 工况1工况4工况5工况6ωx0.2650.26380.27860.2764A/m00.03000.02400.0180An/m00.01250.00700.0035(Aλ/Lpp)/m00.01500.00960.0054 对一个波浪遭遇周期内每 0.25 个周期时刻的伴流场进行探讨,选取工况4情况下不同时刻对应伴流场如图9所示. 定义波峰位于桨盘面位置处时为t/Te=0时刻,此时流体质点轨圆运动速度方向与进速方向相同,桨盘面上的轴向速度大于静水中的轴向速度.桨盘面上平均伴流分数处于最小值,伴流速度场表现为速度等值线明显收缩,速度梯度变大,并且从速度场变化可知:由于形势伴流在外半径处数值较小,波浪对形势伴流作用区域影响明显,波峰处于桨盘面位置时,形势伴流和波浪伴流耦合后作用区域面积明显减小;当波谷行进到桨盘面位置时,即t/Te=0.5 时,流体质点轨圆运动方向恰与流场进速相反,且与波峰下速度大小相同,方向相反,这会削减了伴流轴向速度分量,此时伴流场平均伴流分数最大,形势伴流和波浪伴流耦合部分作用范围最广,速度梯度最小.当t/Te=0.25,0.75 时,此时处于波面方程η=0处,这2个位置处流体质点沿垂向方向上的速度分量最大,此时对轴向上的伴流速度场影响最小,理论上轴向速度场应与静水中完全一致. 由图9可知,对于单个周期内桨盘面处的标称伴流场变化来说,只有当波峰和波谷位于桨盘面位置时,即t/Te=0,0.5 时轴向标称伴流场的变化最为明显,当桨盘面处于波面方程η=0位置处时,轴向标称伴流场与静水中基本一致.因此,图10和11仅列出5种不同的波浪工况下t/Te=0,0.5 时刻的无量纲轴向标称伴流场速度分布云图.由图10和11可知,在不考虑船舶姿态变化的影响时,振幅对伴流场影响十分明显,如果不考虑二阶以下项,流体质点的轨圆运动轴向方向上的速度分量表达式为 u=ωAekycos(kx-ωt)+ωkA2e2ky (5) 可见波浪环境下,即使波陡较小时,一个周期内伴流场变化也较为明显.由式(5)可知,流体质点轴向速度大小与振幅有直接关系,振幅越大,波峰波谷处伴流场变化越剧烈,可以明显看出工况2,即波浪振幅最大时,波峰处于桨盘面处时伴流场收缩最剧烈.随着波陡减小,伴流场的收缩效应变小. 图9 工况4的一个波浪遭遇周期下轴向伴流场变化Fig.9 A wave encounter period with axial flow variation in Condition 4 图10 工况2典型时刻下轴向伴流场Fig.10 The typical time with axial flow in Condition 2 图11 工况3~6典型时刻下轴向伴流场Fig.11 The typical time with axial flow in Conditions 3—6 由图11(c)~(h)可知,当波长变小波陡不变时,伴流场几乎无变化.可见,波陡作为决定波动性质的主要因素对伴流场的作用也是如此.当波陡不变,但波高随波长呈一定比例减小时,可看到桨盘面下方的伴流场受到一定影响,这主要是由于波浪中流体质点的轨圆运动离自由表面越远的位置处运动越小,一般认为在无限水深环境中λ/2位置处,其运动可忽略.因此,当波长减小时,处于相同深度的桨盘面的标称伴流场,受到波浪的影响减弱.可以认为,船舶短波航行中,波长对桨盘面上方的速度场影响较大. 图12和13所示为典型半径处无量纲轴向速度的周向分布.横轴θ=0° 时为桨盘面处12点钟方向,每隔10° 取一个速度点,纵轴为桨盘面位置处无量纲的轴向速度.综上所述,波陡越大,流体质点的轨圆运动速度越大,轴向速度分布及伴流峰值受其影响越大,且发生周期性的变化,这意味着船舶在波浪中航行时螺旋桨进流环境与静水中相比变差.由内半径(r/R=0.5)和外半径(r/R=0.9)的轴向速度分布的对比可知,波浪的存在对内半径处的影响明显大于对外半径处的影响;由同一半径处不同时刻的对比可知,波浪的波峰及波谷位于桨盘面位置处时,其对速度场的影响并不完全对称,这与船舶自由表面兴波改变了入射波在船尾的波型分布有关. 图12 不同波陡下典型半径处无量纲轴向速度的周向分布Fig.12 Circumferential distribution of dimensionless axial velocity at typical radius under different wave steepnesses 图13 不同波长下典型半径处无量纲轴向速度的周向分布Fig.13 Circumferential distribution of dimensionless axial velocity at typical radius under different wave lengths 本文利用RANS方法主要对不考虑船舶姿态变化下的波浪伴流场进行了数值计算,通过分析得到的结论如下: (1) 波浪中船尾轴向标称伴流分数呈流体质点轨圆运动相同的周期性变化,但一个周期内平均伴流分数变化相对较小. (2) 波浪伴流分数为负值时主要是由于波浪的二阶Stokes漂移形成的与波浪传播方向相同的平均意义上的质量迁移,并且波浪伴流分数与入射波的圆频率和振幅密切相关. (3) 虽然平均伴流分数的变化较小,但伴流场在一个波浪遭遇周期内的变化实则难以忽略,且当波峰波谷处于桨盘面位置处时,轴向速度场变化最大. (4) 波陡对于伴流场的影响起决定性作用.而当波陡不变波长减小时,对于伴流场形态影响并不明显,波长船长比主要影响了桨盘面下方位置处的速度.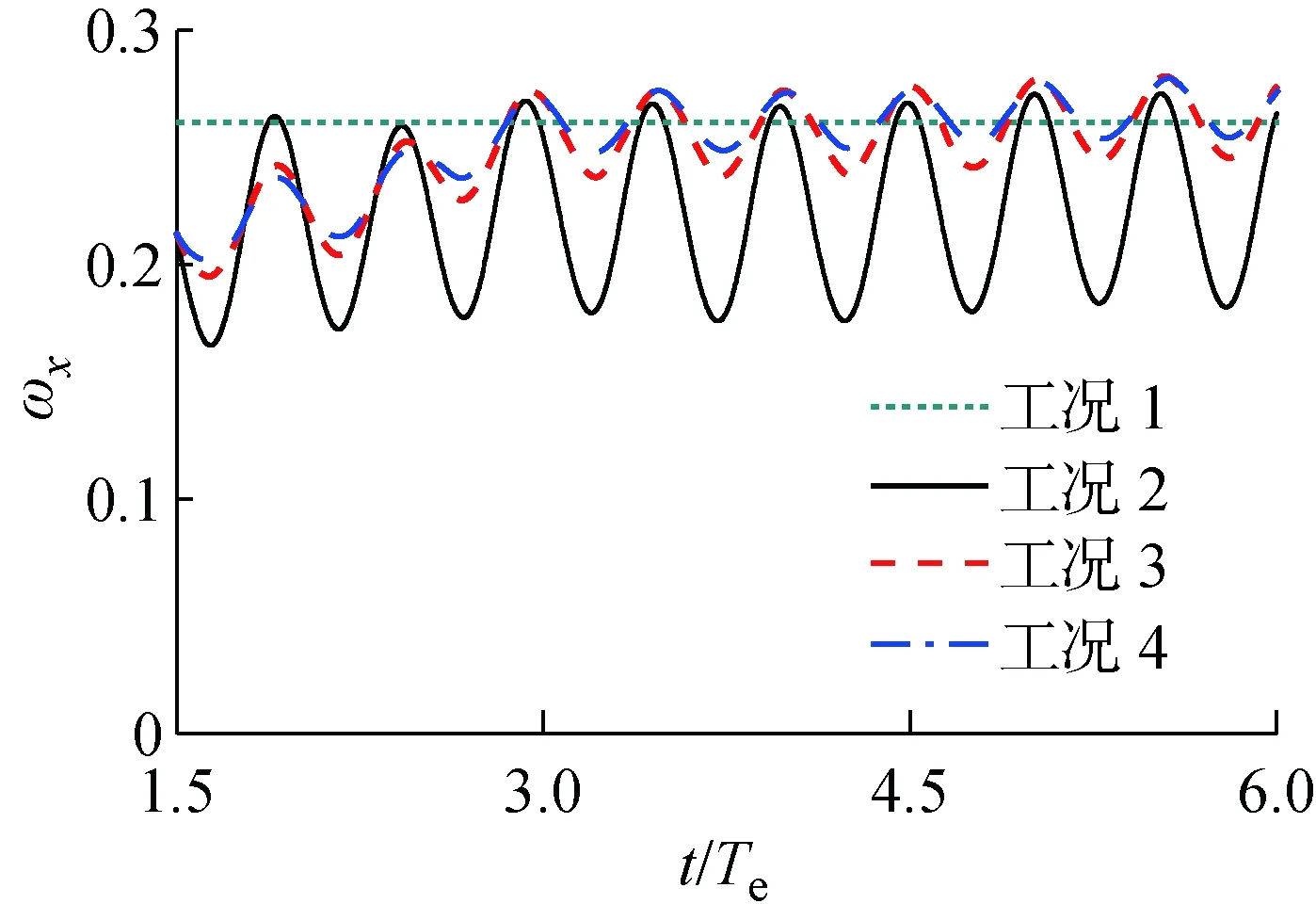
3.2 波长参数对伴流场影响分析
4 伴流场周期性变化分析
5 结论
