摆头转台型五轴机床旋转轴运动误差测量与辨识

郭世杰 姜歌东 梅雪松

(1.内蒙古工业大学机械工程学院， 呼和浩特 010051; 2.西安交通大学机械工程学院， 西安 710049)

0 引言

与三轴机床相比，五轴机床有两个旋转轴，因此它可以同时调节刀具相对工件的位姿[1]，由此可提高加工效率并提升加工表面质量[2]。然而，两个旋转轴也为机床引入了更多的误差源，其中几何误差占机床总误差的40%～50%[3-4]。几何误差是决定机床准静态精度的重要因素，几何误差是几何精度的直接体现，通过实施误差补偿技术可有效保证和提升机床几何精度[5]。误差补偿技术由几何误差建模、误差测量及辨识、误差补偿3部分组成[6]。几何误差测量及辨识是利用几何误差模型实施误差预测的关键，也是进行误差补偿的前提，因此针对五轴机床旋转轴几何误差测量及辨识，国内外众多学者展开了较多的研究[7-10]。几何误差分为运动误差(位置相关几何误差)和位姿误差(位置无关几何误差)两类[11-12]，前者主要源于制造过程，后者主要形成于装配过程。基于多轴同步运动驱动球杆仪(DBB)可实现圆轨迹测量，利用几何误差与圆测量轨迹之间的映射关系，可辨识摇篮式五轴机床旋转轴的位姿误差[13-14]。将DBB安装于旋转轴误差敏感方向上，通过旋转轴单轴运动，可实现旋转轴运动误差辨识[15-18]。在此基础上，设计一次安装状态下的空间轨迹测量，可有效避免安装误差对测量结果的影响[19]。与需进行多组测量轨迹的测量方法相比[20-21]，基于激光跟踪仪[22]及R-test[23]的误差测量方法测量路径较为简单，但需要建立较为复杂的辨识模型。

上述研究对降低旋转轴几何误差的影响起到了重要推动作用，然而机床结构的差异性致使现存测量方法通用性弱。DBB与激光干涉仪、跟踪仪及R-test仪相比成本低，易于实现工业现场的机床几何精度检测[17]，而现有的利用DBB进行旋转轴几何误差的研究主要应用于摇篮式五轴机床，针对摆头转台型五轴机床旋转轴的运动误差测量及辨识的方法较少[20,24]，已有的利用DBB对摆头转台型五轴机床旋转轴运动误差的测量、辨识方法中，装夹次数较多、易受安装误差累积效应的影响。

鉴于此，本文以摆头转台型五轴机床为研究对象，在已有研究基础上提出一种基于DBB的五次安装测量、辨识方法。首先，依据摆头转台型五轴机床旋转轴空间结构特点，对旋转轴运动误差在其局部坐标系下进行表征并建立运动误差测量模型。其次，利用DBB测量过程对误差敏感方向的特征，建立DBB的安装模式并将DBB相同的初始安装位置的测量模式合并，构造基于DBB测量的五次安装法，基于DBB测量值辨识摆头转台型五轴机床2个旋转轴的12项运动误差，通过减少安装次数提升测量及辨识的准确性和精准度。最后，根据所提出的五次安装法旋转轴运动误差检测方案，运用DBB在摆头转台型五轴机床上进行实验，利用辨识结果进行误差补偿前后的精度对比，以验证该方法的有效性与可行性。

1 五轴机床旋转轴运动误差建模

1.1 旋转轴的运动误差

摆头转台型五轴机床结构如图1a所示。摆头转台型五轴机床结构由X轴、Y轴和Z轴3个直线轴，以及C轴和B轴两个旋转轴组成。旋转轴几何误差中的运动误差与运动轴的指令位置相关，即运动误差随着指令位置发生改变。因此C旋转轴及B旋转轴的运动误差可表达为旋转角c及b的函数。旋转轴的6项运动误差如图1b所示。其中，δi(j)表示位置误差，εi(j)表示角度误差，相应的j表示位置坐标，i表示误差所在方向。

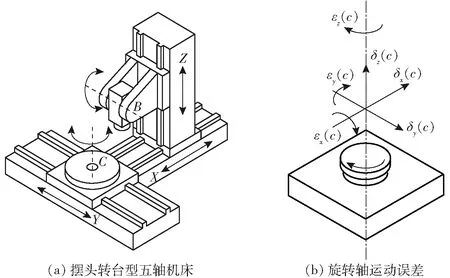
图1 机床结构及运动误差示意图Fig.1 Schematics of machine tool and motion errors

图1a中的摆头转台型五轴机床的B旋转轴具有6项运动误差，分别是X、Y、Z方向的位置误差δx(b)、δy(b)、δz(b)和绕X、Y、Z轴角度误差εx(b)、εy(b)、εz(b)。对C轴而言，6项运动误差分别是3项位置误差：δx(c)、δy(c)、δz(c)和3项角度误差：εx(c)、εy(c)、εz(c)。

1.2 摆头转台型五轴机床测量坐标系的建立

由于运动误差表征运动轴在理想轴线位置方向上的运动偏差，因此依据多体系统理论进行误差建模时，将旋转轴所包含的运动误差在所对应的运动轴的局部坐标系下进行定义和描述，这与运动误差的本质特征相符，也与运动误差表达时矩阵相乘的运算规则相对特征体局部坐标系进行定义的形式一致。

定义机床坐标系位于工作台中心，B轴坐标系XbYbZb与主轴坐标系XsYsZs重合。Y轴坐标系XyYyZy、X轴坐标系XxYxZx、Z轴坐标系XzYzZz建立于各组成轴上，以上局部坐标系方向与参考系XRYRZR一致。C轴和B轴的测量坐标系XcYcZc、XbYbZb与各局部坐标系之间位置关系如图2所示。对摆头转台型五轴机床而言，通过将旋转轴的运动误差固结于所建立的局部坐标系下进行描述，可实现在各旋转轴局部坐标系下的轨迹测量，易于误差建模和辨识的进行。

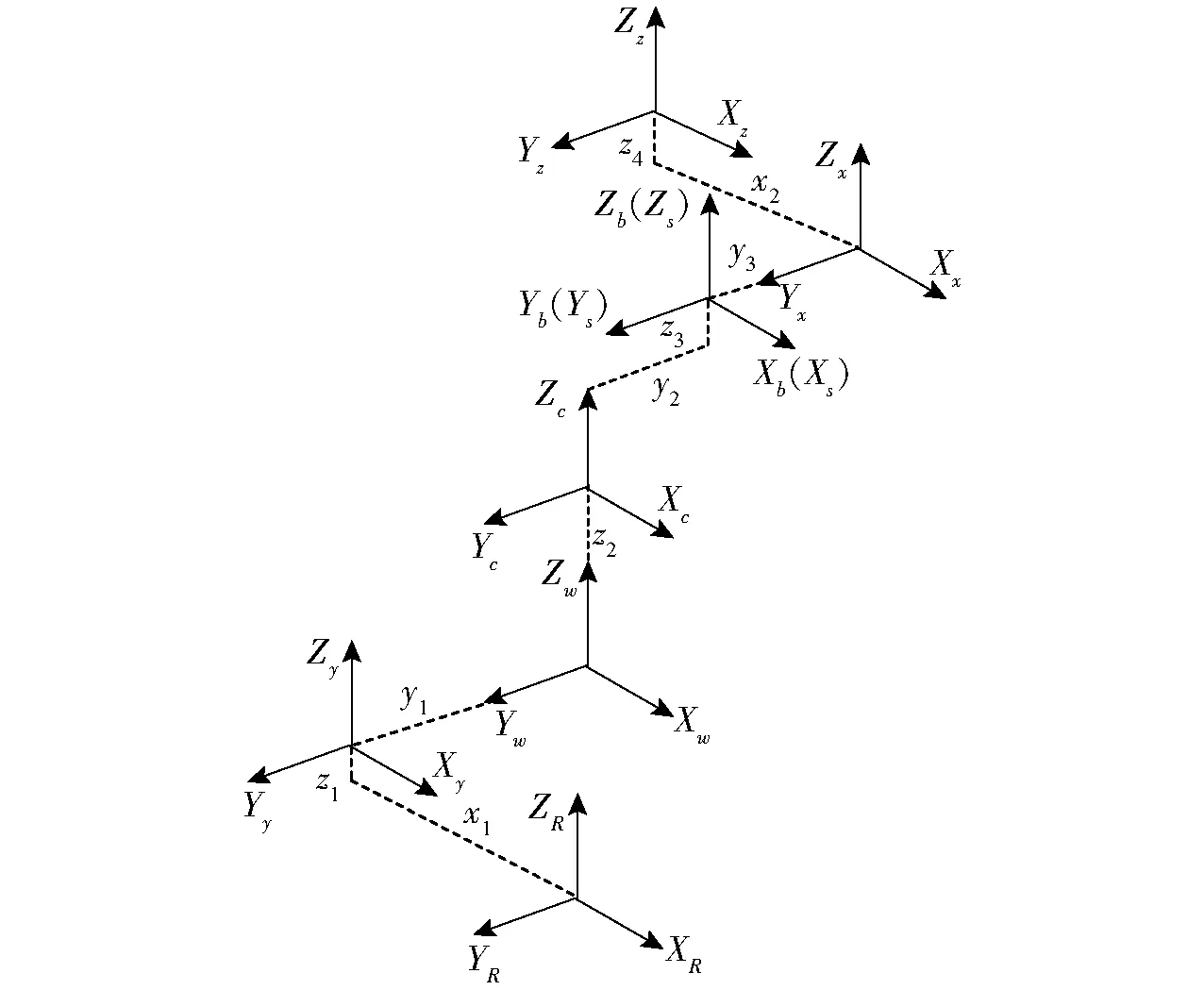
图2 旋转轴局部坐标系示意图Fig.2 Structure schematic of local coordinate systems

1.3 摆头转台型五轴机床旋转轴运动误差测量模型

DBB是检测机床精度的有效工具，在具有圆弧插补功能的数控机床上，可通过多轴联动或主轴端旋转轴转动带动主轴端DBB支座运动，驱动工作台带动安装其上的DBB支座运动，圆运动过程中可伸缩杆检测两接触球球心间距离相对圆运动半径的误差，并形成圆运动的误差轨迹，结合几何误差模型可实现误差解耦及误差项的最终辨识[1,13]。由五轴机床空间几何误差的齐次表达形式可知，五轴机床的特征体i和相邻低序体单元j之间的位置关系可由齐次变换矩阵表示为

(1)

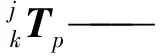
球杆仪的接触球O2和O1在测量坐标系中的位置为Po2=(x2，y2，z2)T，Po1=(x1，y1，z1)T。不考虑运动误差对旋转轴精度的影响时，小球Oj的理想变换矩阵为

(2)

当旋转轴C运动而转动轴B保持静止时，与角b相关的矩阵是单位阵；类似的，当旋转轴B运动而旋转轴C保持静止时，与角c相关的矩阵是单位阵。考虑旋转轴的运动几何误差影响机床精度，小球Oj在实际状态下的变换关系表达为

(3)

利用旋转轴驱动球杆仪实现圆轨迹测量时，DBB的接触Oj的理想位置和实际位置为

(4)

(5)

将式(3)代入式(4)，式(2)代入式(5)，可确定理想状态下DBB接触球之间的距离iL和实际状态下接触球间距离aL，其表达形式为

iL=iPo2-iPo1

(6)

aL=aPo2-aPo1

(7)

DBB接触球之间的长度变化值在3个方向是空间误差向量，可以表示为

[ΔxΔyΔz1]=aL-iL

(8)

将式(6)、(7)和齐次变换矩阵代入式(8)可确定误差向量的具体表达式。对C轴运动几何误差进行测量时，需保证主轴端接触球不受B旋转轴运动的影响，以此实施圆轨迹测量可以得到C轴的空间误差向量，结果为

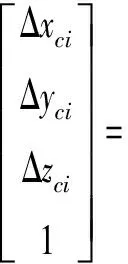
(9)

式中，下标i表示测量模式，下标j表示安装位置。

类似的，对旋转轴B的运动几何误差进行辨识时，将相关的误差矩阵代入式(8)后，可得B轴误差向量表达式为

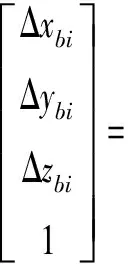
(10)

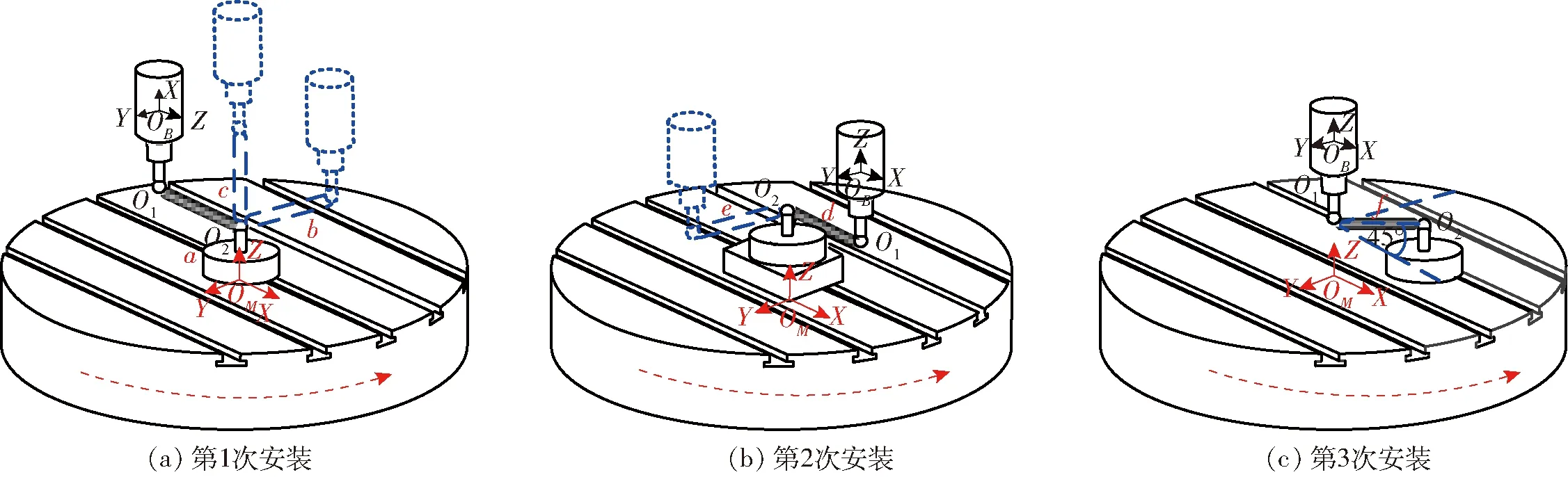
图3 辨识C轴运动几何误差的安装测量模式Fig.3 Installation and measurement modes for identifying motion errors of C axis

2 基于五次安装法的运动几何误差测量及辨识

基于五次安装法的PDGEs测量及辨识的基本思路是：通过设置DBB的接触球在测量坐标下的初始位置，保证旋转轴相同初始安装位置下的圆轨迹测量相继进行，然后改变DBB的安装位置实施下一安装位置下的轨迹测量。利用旋转轴单独运动以及直线轴联动可直接实现一次安装不同测量模式之间的切换，在此过程中DBB的磁致伸缩杆不与两个球面支承座分离，其本质属于同一次安装[19,21]。

2.1 C轴的测量模式及辨识

当测量坐标系与旋转轴的轴心位置重合，且DBB的球杆与测量坐标系的轴线平行时，DBB磁致伸缩杆对相应方向的误差最为敏感[11-12,16]。因此可通过设置球杆仪安装位置和方向，实现DBB的可伸缩杆沿旋转轴坐标系的坐标轴方向相对静止，通过上述处理可有效提升测量及辨识效率。此外，为简化辨识过程、提升辨识结果的准确性，需要限制旋转轴B轴与旋转轴C轴同步运动形式的出现，由此可实现B轴的运动几何误差不影响C轴的辨识结果，即通过设置旋转轴的运动形式保证辨识过程中两个旋转轴的运动几何误差测量过程中的线性无关。

通过上述方式可确保主轴端接触球沿刀具链在机床C轴定义的测量坐标系下位置不发生变化，因此只需考虑安装于转台端C轴坐标下的接触球受C轴运动几何误差的影响。由式(9)和式(10)可知，几何误差在3个方向上的误差分量、球杆仪工作台端接触球位置以及几何误差项之间可表达为矩阵形式，利用最小二乘法可准确辨识6项误差，也可通过设计不同测量位置，利用测量坐标系内不同位置的圆轨迹测量数据确定6项几何误差解析解。

由运动误差的矩阵表达形式可知，运动误差与机床的综合几何误差模型无关，仅与测量模型相关。因此需考虑测量坐标系下误差项与DBB安装位置之间的关系，选择合适的坐标位置使上述包含位置坐标的矩阵形式为非奇异矩阵，由此构造出6个线性无关的正定方程。式(9)、(10)中(xi，yi，zi)(i=1,2,…,6)是工作台一侧接触球在C轴坐标(测量坐标)系下的初始安装位置。测量过程中，DBB对使其伸缩杆产生位移变形方向的误差最为明显，因此，可据此设计球杆仪的放置方向。对C旋转轴所设计的DBB安装位置如图3所示。

设置上述3次安装并建立a～f测量模式，此时对C轴的测量需要3次安装。具体步骤如下：

如图3所示，在对DBB实施第1次安装并进行模式a下的圆轨迹测量时，工作台端小球O2安装于转台中心，球杆仪的伸缩杆平行于X轴，主轴端接触球O1与接触球O2距离为DBB的公称长度L。测量过程中，仅有旋转轴C轴运动其他运动轴均保持静止。此时在C轴的驱动下仅有工作台端小球运动，主轴端接触球O1静止。这样球杆仪仅对旋转轴C轴X方向的误差敏感，即仅有C轴沿X方向的误差对测量有影响。在此时测量模式下，球杆仪测量值ΔR与几何误差的关系为

ΔRCa=Δxca=δx(c)

(11)

类似的，在b、c测量模式下进行沿Y轴和Z轴方向的安装时，可实现对C轴沿Y方向和沿C轴Z方向的误差测量。此时，在b、c测量模式下，球杆仪测量值ΔR与几何误差的关系为

ΔRCb=Δycb=δy(c)

(12)

ΔRCc=Δzc=δz(c)

(13)

图4 辨识B轴运动误差的安装测量模式Fig.4 Installation and measurement modes for identifying motion errors of B axis

在对DBB实施第2次安装并进行模式d下的圆轨迹测量时，首先在Z方向上提升工作台端接触球O2与转台中心的距离后，改变B轴与接触球O1的距离后对球杆仪进行安装。与第1次安装下的测量模式a类似，球杆仪的伸缩杆平行于X轴，主轴端小球O1与O2距离为DBB的公称长度L。测量过程中，仅有旋转轴C轴运动，其他运动轴均保持静止。由于工作台端小球安装位置的改变，在Z方向测量坐标系与小球O2的球心位置不重合，除了C轴沿X方向的误差对测量有影响外，C轴沿Z方向的误差也会对测量有影响。由于在测量模式a中已经辨识了C轴沿X方向的误差δx(c)，此时C轴沿Z方向的运动误差可辨识，二者与球杆仪读数之间的关系可表达为

ΔRCd=z4εy(c)+δx(c)

(14)

类似的，在e测量模式下进行沿Y的安装时，可实现C轴沿Y方向的误差测量。此时，球杆仪读数的相对表达形式ΔR可表达为

ΔRCe=-z5εx(c)+δy(c)

(15)

在对DBB实施第3次安装并进行模式f下的圆轨迹测量时，球杆仪的安装如图3c所示。此时主轴端小球位于转台中心上方，DBB的可伸缩杆平行于XOY平面，且工作台端接触球O2的初始位置在X轴与Y轴的角平分线。测量过程中，仅有旋转轴C轴运动，其他运动轴均保持静止。由于工作台端接触球O2的改变，在XOY平面内C轴沿X方向的误差和C轴沿Z方向的误差均对测量有影响，此时影响测量轨迹的误差与球杆仪读数之间的关系可表达为

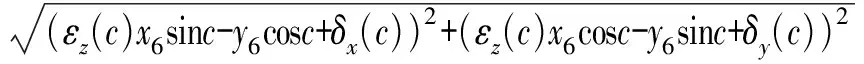
(16)

由式(11)～(16)可知，确定工作台端小球O2的初始安装位置后，δx(c)、δy(c)、δz(c)、εx(c)、εy(c)可由式(12)～(15)确定辨识值，将测量模式a和测量模式b辨识出的几何误差δx(c)、δy(c)的解析解代入式(16)后可辨识出滚转误差εz(c)，由此可辨识C旋转轴的6项运动几何误差。

2.2 B轴测量模式及辨识

由于B轴的坐标系与工作台之间的空间距离较大，无法将球杆仪的磁性底座准确安装于B轴的轴线上，因此对B轴的测量辨识与C轴的测量及安装模式不同。当B轴转动带动主轴端小球运动时，需要通过直线轴与旋转轴的联动方式实现圆/圆弧运动轨迹的测量。

对B轴测量时以B轴的局部坐标系为测量基准坐标系。图4是设计的DBB安装示意简图。在对DBB第1次安装后进行B轴a模式下的测量，主轴端接触球O1安装于距离B轴沿X方向Lb处，工作台端接触球O2在B轴坐标系下的位置是(R+Lb, 0,H1)。DBB第1次安装后的B轴a测量模式下，进行圆轨迹测量过程中B轴顺时针转动，Z轴与X轴通过直线插补形成圆弧轨迹，C轴和Y轴保持静止。

DBB对B轴沿X方向的几何误差敏感，此时接触球O2与O1之间的距离在X轴方向的投影表征了球杆仪长度。几何误差影响下的球杆仪长度变化与误差项之间的关系为

ΔRBa=Lbεy(b)sinb+δx(b)+H1εy(b)cosb

(17)

在对DBB第1次安装后测量模式b下，此时球杆仪对B轴沿Y轴方向的误差敏感。通过B轴的顺时针转动，Z轴与X轴通过直线插补形成圆弧轨迹，C轴和Y轴保持静止。几何误差影响下的球杆仪长度变化值与误差项之间的关系为

ΔRBb=δy(b)+H1(εz(b)sinb-εx(b)cosb)

(18)

在对DBB第2次安装后c测量模式下，几何误差影响下的球杆仪长度变化值与误差项之间的关系为

ΔRBc=H1εy(b)cosb+δx(b)

(19)

在对DBB第2次安装后的d测量模式下，主轴端接触球O1在B轴坐标系下的位置是(R,0,H1)，工作台端接触球O2安装于X轴方向上，在B轴坐标系下的位置是(R,0,H1-R)，此时DBB的可伸缩杆平行于Z轴。几何误差影响下的球杆仪长度变化与误差项之间的关系为

ΔRBd=-H1εy(b)sinb+δz(b)

(20)

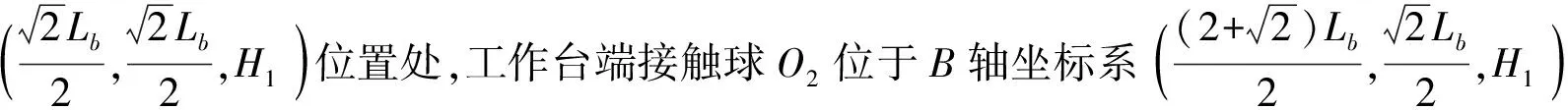
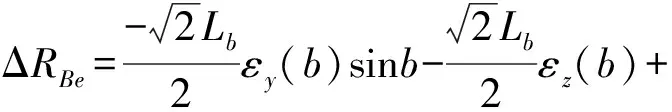
(21)

在对DBB第4次安装后的测量模式f中，主轴端接触球O1安装于B轴坐标下的(0,0,H2)处，工作台端接触球O2安装于坐标系下(0,R,H2)处。DBB的可伸缩杆平行于Y轴方向。此时，几何误差影响下的球杆仪长度变化与误差项之间的关系为

ΔRBf=H2[εz(b)sinb-εx(b)cosb]+δy(b)

(22)

通过测量模式a的辨识表达式(17)和测量模式c的辨识表达式(19)可知角度误差εy(b)的辨识表达式为

(23)

将式(23)代入式(20)，可得δz(b)的表达式为

(24)

将式(23)代入式(19)，可得δx(b)的表达式为

(25)

求解式(21)，可得到角度误差εz(b)的辨识表达式为

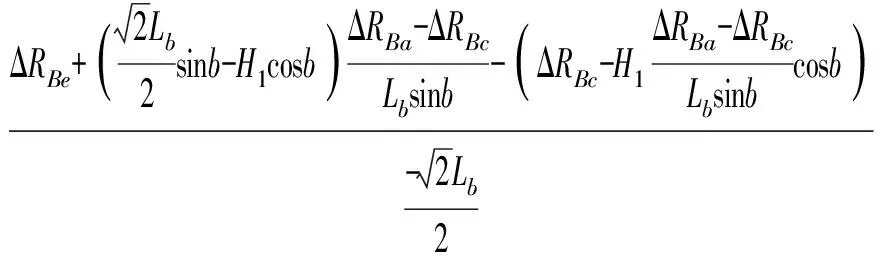
(26)

基于已经辨识的εz(b)，由式(18)和式(22)可辨识出εx(b)，其表达式为

(27)

利用εz(b)的辨识值，可以确定δy(b)的辨识表达式为

(28)

2.3 五次安装法的建立

B轴坐标系中心位置距离工作台表面沿Z向距离较大，这导致构造B轴的运动几何误差辨识方程时DBB的安装位置较C轴多。但依据在相同的初始安装位置可连续实施不同平面内的测量，且球杆仪仅需安装一次的特点，本文将相同的初始安装位置的测量模式合并构造基于DBB测量的五次安装法。

由C轴和B轴所述的DBB安装及测量特征可知：旋转轴C轴的测量模式d、e与测量B轴的测量模式f相比，主轴端接触球和工作台端接触球在机床坐标系下的初始位置存在相似之处。此时可利用旋转轴单独运动以及直线轴联动直接实现一次安装不同测量模式之间的切换。类似的情况在C轴测量模式f与B轴测量模式c、d之间也存在。因此，本研究所提出的测量方法可依据上述特点进行安装次数的简化，基于DBB测量流程如图5所示。

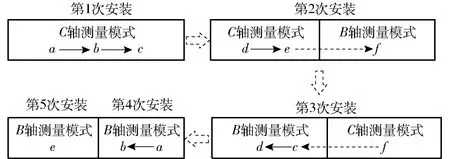
图5 基于DBB测量的五次安装法测量流程Fig.5 Measuring process of five installation method based on DBB

图6 五次安装法实验现场Fig.6 Experimental setup of five installation method

五次安装法与其他方法[19-20]相比可有效减少DBB的安装次数，这样可以节省安装时间，同时可进一步避免安装误差对测量结果一致性的影响。

3 实验验证

为验证所提出的五次安装测量方法的准确性，在如图6所示的五轴加工中心上进行实验研究。在进行旋转轴的运动几何误差测量前，先进行直线轴的几何误差测量及补偿[1,11]，环境温度控制在(20±2)℃内，由此最大程度降低热误差对测量结果的影响。

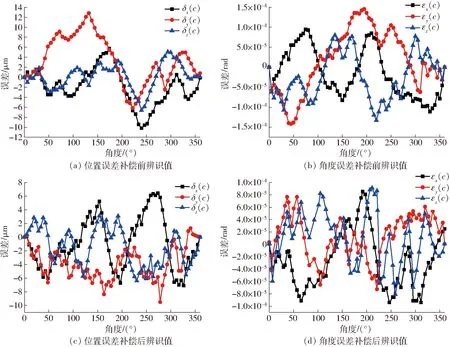
图7 C轴运动误差辨识结果对比Fig.7 Comparison of motion errors of C axis

依据五次安装法建立的测量模式，利用杆仪进行圆轨迹测量。整个测量过程包括DBB的五次安装，其中安装参数Lb=100 mm，R=100 mm，H1=384.67 mm，H2=484.67 mm。C轴安装模式下，B轴静止不动，C轴的进给率500 mm/min，C轴的越程角为180°，顺时针和逆时针的运动行程是360°。B轴运动模式下，B轴的进给率是500 mm/min，B轴的越程角为5°，顺时针和逆时针的运动行程是90°。同一测量模式进行多组数据测量，并保存数据。依据五次安装法测量流程执行完上述的圆轨迹测量后，利用所建立的辨识模型可解耦得到C轴和B轴的12项运动几何误差，辨识结果如图7、8所示，利用辨识值通过逆运算确定补偿值的解析解[8,13]。

由图7可知，误差补偿后C轴的位置误差最大值由12.83 μm降低至9.53 μm，角度误差最大值由1.45×10-4rad降低至7.0×10-5rad。C轴的最低补偿率是15.85%，平均补偿率是48.89%，最大补偿率达到了92.42%。

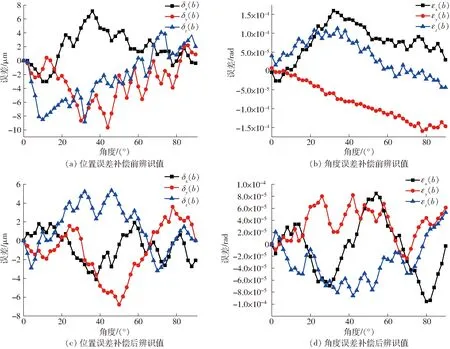
图8 B轴运动误差辨识结果对比Fig.8 Comparison of motion errors of B axis

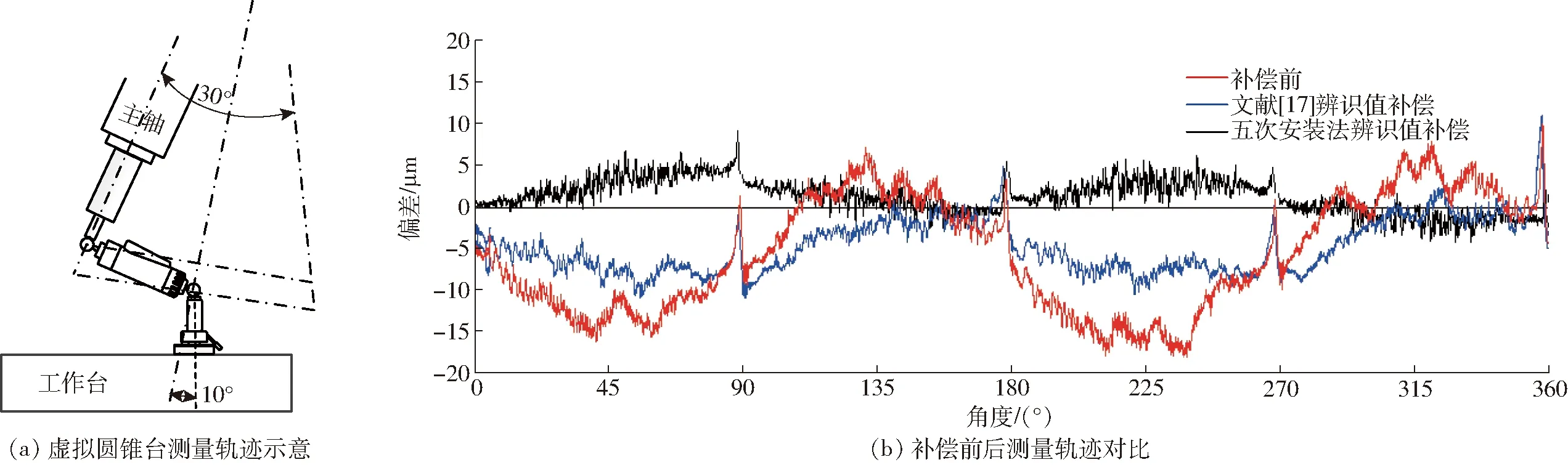
图9 圆锥台测量轨迹及测量结果Fig.9 Measurement track and measurement results of frustum of cone

由图8c和图8d可知，误差补偿后B轴的位置误差最大值由9.65 μm降低至7.11 μm，角度误差最大值由1.6×10-4rad降低至2.0×10-5rad。B轴的最低补偿率是26.45%，平均补偿率是51.49%，最大补偿率达到了87.26%。为进一步验证辨识值的准确性，依据ISO 230-1标准利用五轴同步运动驱动DBB进行虚拟圆锥台轨迹测量[12,25]，并分别进行误差补偿前空间圆锥台轨迹测试(测量轨迹如图9a)，以及依据文献[17]的测量方法(六次安装)和本文的五次安装法确定辨识值，并进行误差补偿后空间锥台轨迹测量，结果如图9b所示。

由图9b可知，运动误差补偿前圆轨迹的半径偏差平均值达9.5 μm，依据文献[17]所提出的测量辨识方法确定几何误差数值实施误差补偿后，圆轨迹的半径偏差平均值为6.8 μm，利用五次安装法进行误差辨识及补偿后，圆轨迹的半径偏差平均值为4.7 μm，降低了50.52%。采用文献[17]的测量辨识方法进行补偿后，半径偏差明显降低，依据五次测量法的辨识值进行误差补偿后，半径偏差分布范围进一步减小。误差补偿实施以后效果显著，机床的精度得到了有效的提升。这说明本研究所提出的误差测量及辨识方法可准确量化摆头转台型五轴机床旋转轴的运动误差数值，较少的安装次数提升了辨识结果的准确性。

4 结论

(1)运用多体系统理论和齐次坐标变换方法对几何误差进行表征，建立了摆头转台型五轴机床旋转轴运动误差测量模型。将旋转轴的运动误差在其相应的局部坐标系下进行表达，无需考虑机床的参考坐标系，符合运动误差仅与旋转轴自身制造精度相关，与轴间装配精度无关的本质特征。

(2)根据目前机床检测精度高、速度快的要求，提出了一种基于DBB的五次安装的摆头转台型五轴机床旋转轴运动几何误差测量、辨识方法。通过设置DBB的接触球在测量坐标下的初始位置，保证旋转轴相同初始安装位置下的圆轨迹测量相继进行，利用旋转轴单独运动以及直线轴联动可直接实现一次安装不同测量模式之间的切换，通过基于DBB圆轨迹测量的五次安装，可实现两个旋转轴的12项运动误差的全部辨识。减少了安装次数，最大程度避免了安装误差对测量结果的影响，提升了测量效率。

(3)依据五次安装法在摆头转台型五轴机床上进行运动误差辨识，利用辨识值实施误差补偿后，C轴的最低补偿率达到15.85%，平均补偿率为48.89%；B轴的最低补偿率是26.45%，平均补偿率达到51.49%，五轴同步运动形成的虚拟圆锥台测量轨迹的半径偏差降低了50.52%，误差补偿后机床精度得到显著提升，说明本研究所提出的误差测量及辨识方法对量化摆头转台型五轴机床的运动误差准确、有效。