多源信息多尺度视角的南京市街道级人口模拟研究

许玲丽，颜梅春

(河海大学地球科学与工程学院，江苏 南京 211100)

人口一直是城市发展的重要因素，精准把握人口分布可为生态环境建设、社会经济政策制定和城市规划提供重要参考[1]。目前传统调查人口数据的方法效率低、周期长，调查结果时效性和空间性差[2]。随着科技的发展，利用大数据和遥感技术探寻城市人口分布逐渐成为热点,分别考虑城市灯光亮度、土地利用类型、交通发达程度、城市建筑类型和布局等，或尝试集成多因素建立相关模型来构建人口估算模型[3-6]。在利用多源数据进行精细尺度的人口模拟，信息的综合利用及适应的尺度和方法等方面都有诸多问题亟待解决[2，7]。

夜间灯光数据能够反映夜晚灯光强度、范围、分布形状，已经广泛应用在城市建成区提取[8]、城市GDP模拟[9]、人口预估、经济发展[10]、城市景观格局分析[11]等方面。如文献[12]基于Landsat 8数据和夜间灯光数据DMSP/OLS，提取鬼城指数来构建不同指数级别人口空间模型；文献[5，13]利用土地分类数据和夜间灯光数据DMSP/OLS对人口空间化模型进行优化；文献[14]在1996年率先提出对DMSP的夜间灯光数据与人口、GDP和耗电数据的空间关系进行分析研究，得出灯光数据与人类活动有着很强的相关性。与DMSP/OLS夜间灯光数据相比，新一代NPP/VIIRS灯光数据具有更高的时空分辨率，在城市人口、经济、社会生活中起着很大的作用[15-16]。但该数据获取的时间偏晚，不能完全反映区域人口活动状况。因此，利用夜间灯光数据结合其他信息可以更客观准确地进行城市人口估算模拟。

国内外有许多基于夜间灯光遥感影像研究人口密度或人口分布的，多数是基于土地利用分类数据进行估算；也有将夜间灯光数据与其他因素的因子结合分析的，但基本上都是基于区县级以上尺度的研究，对于其内部各区域的差异考虑较少。不同区域其开发程度不同导致经济发展情况不同，人口分布状况也不同，因此估算的模型也不同。如今是大数据时代，网络媒体数据极其丰富，商贸、服务行业的数量和分布更是人口分布的侧影，对人口估算有很重要的影响。基于以上原因，本文研究拟从城市的3个尺度，即市级、市郊级和城市化度的层面，以南京市街道级行政区的人口密度和人口总量为基本单元对象，探讨新一代NPP/VIIRS夜间灯光数据、IBI指数和POI数据在人口估算中的作用，以及其影响程度和模型，以拓展城市人口估算的广度和深度。

1 研究区与数据预处理

1.1 研究区域概况

南京市地处长江三角洲地区，是我国东部沿海经济带与长江经济带战略交汇的重要节点城市，辖玄武、秦淮、建邺、鼓楼、雨花台、栖霞、江宁、浦口、六合、溧水、高淳11个区，共有83个街道、17个镇，全市行政区域面积6 587.02 km2，2016年末全市常住人口总量827万人，人口分布具有典型性。

1.2 数据来源与预处理

数据包括：国家基础地理信息中心的南京市行政边界图；南京市2010年人口普查数据(以街道为单元)；2017年大众点评网南京市共37 726个餐饮商家POI数据。

采用来自地理数据空间云的Landsat 8数据(2017.10)，对Landsat 8影像进行数据预处理(如大气校正、辐射校正和GS(gram-schmidt pan sharpening)方法波段融合)，得到15 m分辨率的多光谱数据作最大似然法分类(5类)以备辅助参考。利用NOAA官网的2017年NPP/VIIRS数据进行噪声滤除剔除异常值[17]。南京市的POI、土地利用和夜间灯光分布基本情况如图1所示。

2 研究方法

首先提取建筑用地IBI指数，用IBI指数设置阈值划分市郊,然后根据人口密度进行城市化度分级，最后利用不同数据源及组合分别进行市级、市郊级和城市化度级3个层面尺度的多种关系模拟。具体过程如下。

2.1 建筑用地指数IBI提取

城市的土地利用程度，尤其是城市建成区的建筑用地占比反映了人口聚集程度[5，13，18]。IBI指数是近些年广泛使用的，用于提取城市建筑用地范围[19-20]的建筑用地指数，其计算方法参见文献[20]。通过Landsat 8的OLI数据计算IBI指数，水体值的范围为0～0.5，植被为0.5～0.6,建成区为0.6～1。将提取的IBI指数栅格图分别与南京市遥感影像图、土地利用分类图叠加，契合度好，表明IBI指数提取的城市建筑区精度较高，适用性强，但无法区别建筑用地是城市还是乡村[20]，因此需要进行后续处理。

2.2 基于小面元过滤的市郊划分

区域开发和发展通常是集中连片的，在IBI建筑用地图像中，连片大面积区域为开发程度高的城市市区范围，碎小区域或呈点状分布的区域为开发、发展水平低的农区或郊区范围[20]。进行市郊分级，使用小面元过滤的方法：首先，将建筑用地IBI二值化；其次，运用八邻域算法进行邻域聚类，去除区域图层中的碎小面积的斑点、斑块，得到若干平滑独立的小面元，即连通斑块的像元数；最后，采用ENVI中的过滤工具(Sieve Classes)，设置过滤阈值范围。南京市发展水平较高，开发区域分布范围广，过滤面元的阈值设置较大才能得到较明显的城市分级，7001为建成区阈值，1001为郊区阈值。

2.3 街道城市化程度划分

由于市内夜间灯光辐射值方差大，因此有必要对建成区进行城市化度分级分析。人口密度是城市化程度的主要体现，本文按照人口密度进行城市化程度分级。结合文献[21—22]，对南京市100个乡镇、街道按照人口密度将其分为3个等级，0～2000人/km2为第三等级低度城市化区、2000～10 000人/km2为第二等级中度城市化区、10 000 人/km2及以上为第一等级高度城市化区。低度城市化区主要分布于南京市周边地区，有大范围的农田，开发较晚或未开发。中度城市化区集中于居民区，人口密度和灯光强度中等，不会有灯光值突增或极值的情况。高度城市化区在建成区核心范围内，建筑组团复杂，商业活动点集中且遍布于居民区，人口密度和灯光强度最大且灯光有叠加。

2.4 回归分析

结合POI数据、IBI指数和NPP/VIIRS数据3个指标，与人口数据进行单因素及多因素的线性、幂、指数和对数函数模拟，探求不同因素与人口总量和人口密度间的相关性，同种因素与人口总量和人口密度间不同函数关系的确定性系数，构建人口模拟模型POPi={IBIi,Ni,Pi}，其中，i为街道，POP为人口总量，IBI为建筑指数，N为灯光总值，P为餐饮商家数据。

3 结果与分析

3.1 单因素的相关性分析

统计不同因素的总值与人口总量、均值与人口密度关系，得到不同函数回归模型确定性系数最佳的结果，见表1。

表1基于南京市数据的回归分析统计(t表示总量，a表示密度或均值)

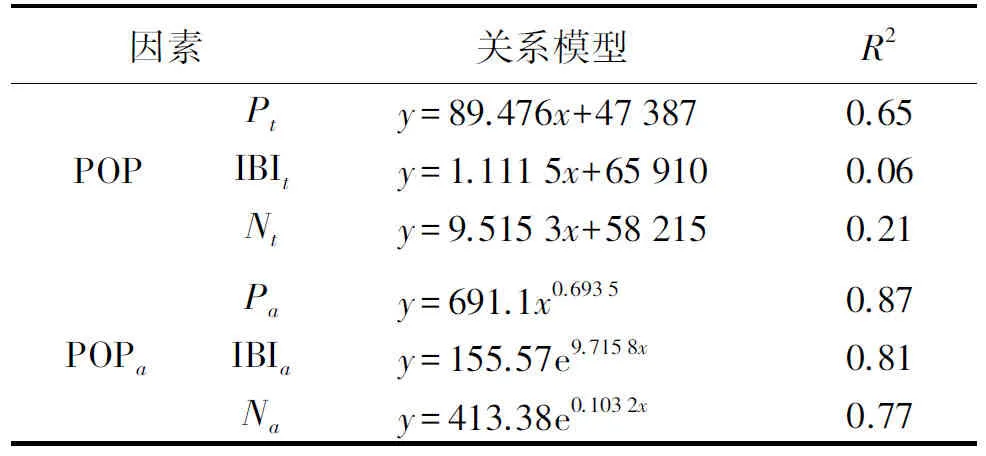
因素关系模型R2Pty=89.476x+473870.65POPIBIty=1.1115x+659100.06Nty=9.5153x+582150.21Pay=691.1x0.69350.87POPaIBIay=155.57e9.7158x0.81Nay=413.38e0.1032x0.77

由表1可见，采用平均值进行回归分析得到的确定性系数R2普遍大于采用人口总数进行回归得到的R2，说明各自变量的平均值或“密度”与人口密度的相关性更强，因为密度更能体现资源分配和利用状况，总量具有模糊性；从单因素来看，餐厅和商家数量最能体现人口数量和人口密度，因为民以食为天。对于变量是平均值(如餐厅商家分布密度)的，线性关系都不是最合适的，人口密度和POI指数是幂函数，R2为0.87，与IBI指数和NPP/VIIRS均值是指数函数，R2分别为0.81和0.77，因为社会经济活动具有竞争、盲目、随机性和不确定性。

3.2 基于市郊分级的人口模拟

结合IBI指数通过ENVI中的小面元过滤的方法，得到市区街道共80个，郊区街道共20个。分别统计市区、郊区人口与灯光数据，并计算不同区域夜间灯光数据的标准差，辅助分析不同区域内的灯光值的差异，得到人口密度与灯光平均值的函数关系，如图2所示。市区的指数函数模型最优，R2为0.7，郊区线性函数最优，R2为0.86。

由图2可见，建成区(市区)在人口密度较小的区域分布紧凑，随着人口密度增大，数据点开始分散。郊区街道灯光标准差在1以下，该域内灯光强度分布较均匀，除江心洲和长芦2个街道外，数据分布于回归线两侧，灯光亮度小且分布紧凑，线性回归相关性系数高达0.86。郊区的人口密度(线性回归)效果优于建成区的人口密度(指数函数)，主要由于建成区高楼林立，灯光叠加饱和，夜灯数据无法传递实际的灯光数量造成的。

3.3 基于城市化程度分级的人口模拟

分别对研究区内各级城市化度的街道数据进行模拟建模，选择最优的结果，见表2。

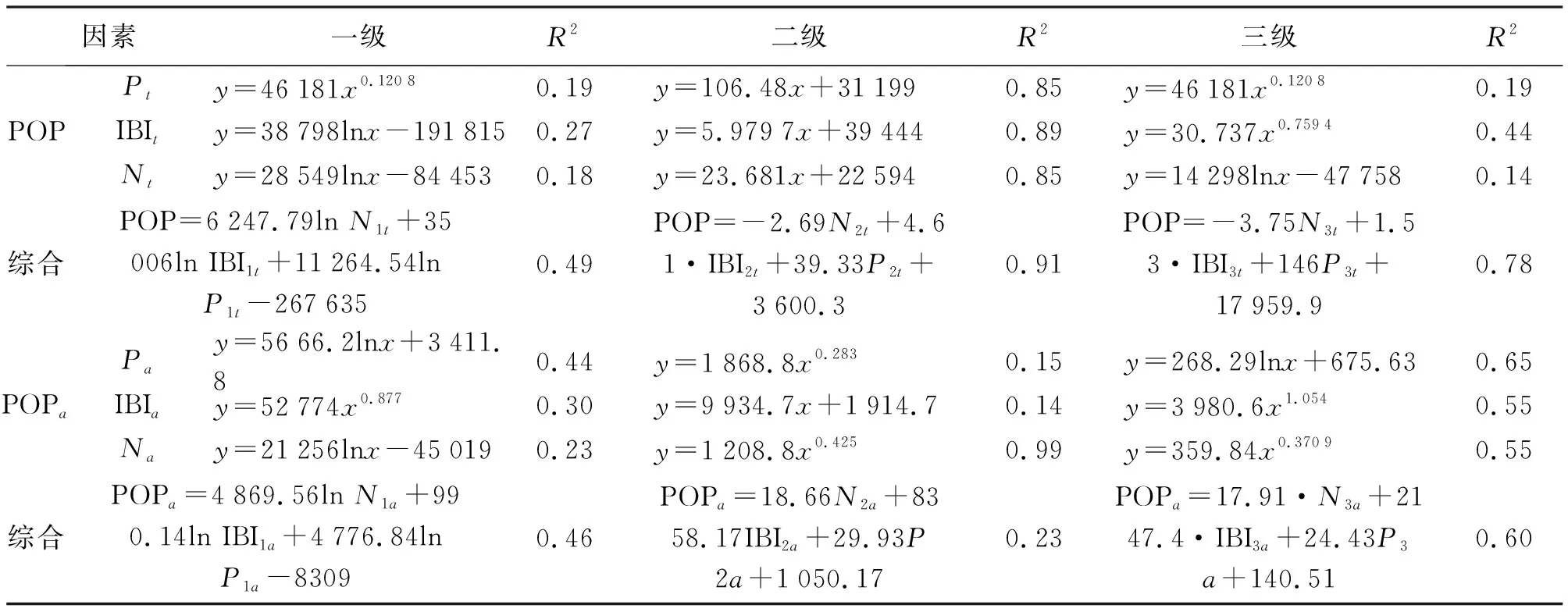
表2 基于人口密度分级数据的分析统计(t和a的含义同表1，数字表示等级)

由表2可知，第一等级即高度城市化区域，各模型的确定性系数均在0.3左右，与人口数据的模拟效果都很差，原因是由灯光饱和、人口的高度集中和商业集聚效应导致；第二等级即中度城市化区域内，基于总数据量的模拟效果更加显著，各种模型的R2均在0.8以上，相关性非常强，原因是城市居住区的人口和设施基本配套且均匀分布；第三等级即低度城市化区域内，基于总数据量的模拟效果都比较差，相较而言，基于平均值数据的回归效果较好，相关性基本在0.5～0.65之间，因为人口和产业都稀疏更容易造成空间上的不对等。其中，POI的密度对人口密度的响应程度较高，相关性更强，原因同前。

不同因素与人口的模型效果都有影响，故综合建立三者与人口数量的多元关系模型，只有二级的人口密度综合模型没有通过0.001显著性检验。由表1、表2可知，二三级总数据、三级平均数据的多元线性回归效果都在可接受范围内，人口总数据在高度城市化街道的最佳对数模型的R2为0.49，中度的线性R2为0.91，低度的线性R2为0.78。说明中度城市化的区域只利用单因素也可以较好地估算人口，多因素更好，高度城市化区域的人口模拟最复杂，仍然面临困难。

城市中心人口密集，商业活动频繁，人口流动量大，受影响因素较多，本文只分析夜灯数据、餐饮店铺数据、建筑用地指数的相关性，未考虑其他主观和不确定因素。人口统计数据是2010年的,与2017年的多源数据存在时间上的出入，但是城市、居住区变化很小，因此对市区、高度和中度城市化区域的结果和结论基本不受影响。

4 结 论

本文以遥感IBI指数、NPP/VIIRS数据和POI数据作为人口响应变量，对南京市作一元线性、指数、对数、幂函数4个模型模拟，根据街道城市化分级、城市和郊区分层分析。结论如下：

(1) 市级。单因素回归分析模型中，3个变量基于平均值的幂函数模型最佳，且POI>IBI>NPP/VIIRS。因此，适于建立餐厅商家分布密度数据幂函数一元回归方程估算南京市人口密度。

(2) 城市化程度。中度城市化区域人口模拟效果最好，不同函数模型效果相近，且IBI指数最佳；城市化程度低的区域适合基于平均值数据的建模；城市化程度高的区域不适合作此分析。

(3) 综合考虑多元线性回归分析中的拟合优度值、方差分析和显著性，可以得到城市化程度高区域适合采用多元对数函数回归模型估算人口密度；城市化程度中等区域适合采用模型的可选范围较广，不同函数的回归模型都较适合，线性模型最佳；城市化程度较低的区域适合采用多元线性回归模型。