喷水推进三体船阻力与自航数值模拟研究
2019-03-06戴原星张志远刘建国王金宝
戴原星 张志远 刘建国 王金宝
(中国船舶及海洋工程设计研究院 上海200011)
引 言
近年来,高性能船舶的发展受到造船界和各国海军的密切关注,三体船是应运而生的一种特种高性能船型。所谓三体船就是由三个船体组成,三个瘦长的船体共享一个主甲板及上层结构,其中间为主船体,两侧并肩各有一个大小相同的辅助片体,主体与片体之间由连接桥连接[1],见下页图1。与单体船相比,三体船甲板面积宽敞,舱室容积增大;瘦长型主船体是为最小阻力和优化航速而设计的。在恶劣海况下,外侧船体为保持较高航速提供了稳性和增加了耐波性。高速三体船采用喷水推进具有明显的优势:相比于螺旋桨推进,喷水推进无附体,阻力小;高速工况下抗空泡性能优越;喷水推进操纵性好。

图1 三体船船体布局示意
喷水推进与三体船的相互作用成为三体船水动力性能的研究热点,研究的主要方法有理论分析、船模试验和数值计算。模型自航试验是船舶在设计阶段预估实船性能的有效手段,但喷水推进由于流道在船体内部,其推力与船体阻力很难分离。随着CFD数值模拟技术的发展,可以有效估算喷水推进与三体船的相互作用的水动力性能。Tomohiro Takai[2]、Frederick Stern[3]、Pablo M.Carrica[4]等基于 Ship-Iowa 并采用重叠网格对水面船舶、潜艇的自航及操纵数值模拟开展了系列研究工作,对URANS方法用于高速轴流式喷水推进船模的自航模拟开展了确认与验证研究;霍聪[5]对目标船在垂直面内三自由度运动及其喷水推进器叶轮随船轴高速旋转的耦合运动进行数值模拟,揭示了流道内部、船体外部兴波以及喷水推进内部的流动特征。本文基于STAR-CCM+软件,开展船模、阻力自航的数值模拟,为喷水推进与高速三体船的总体匹配设计提供参考。
1 基本控制方程和数值模拟方法
1.1 基本控制方程
本文采用数值计算方法中常用的雷诺时均方法进行数值模拟,它将非定常的湍流运动看作时均流动和瞬时脉动流动的叠加。将基本的N-S方程引入Boussinesq假设,得到的流动控制方程为时均形式的连续方程和N-S方程(简称RANS方程)[6]:
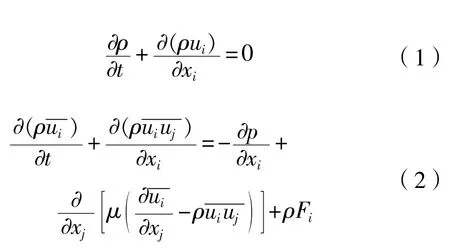
式中 :Fi为体积力,N,包括推进泵旋转过程中流体的科氏力和离心力;p为作用在流体上的压力,Pa;ρ为介质密度,kg/m3;μ为介质的运动粘性系数,选择标准k-ε模型,引入关于湍动能耗散率的方程后形成的两方程模型,对RANS方程组进行封闭。
1.2 VOF多相流模型
船舶计算流体力学往往涉及到对自由液面的模拟,对于喷水推进船的数值模拟,由于喷射的水流直接喷射到空气中,需要考虑到自由液面问题。自由表面问题的处理实际上就是追踪两种介质之间的运动界面,现有的运动界面追踪问题的数值求解方法主要包括 VOF(Volume of fraction)、Level set、波前追踪法(Front tracking method)等。VOF模型是在1981年由Hirt和Nichols[7]提出来,该方法可以处理具有空气和液体具有交界面的稳态和瞬态等问题。VOF模型在整个计算域内对互不相溶的流体求解同一组动量方程,并追踪每种流体的体积分数来模拟多相流。基于VOF方法求解船舶两相流问题时,单位界面通量插值格式有几何重建(Geo-reconstruct)格式、施主-受主(Donnor-acceptor)格式等。几何重建格式假定两相流体在每个计算单元内的分界面为有线性斜率的折线,并用此线性斜率计算流体通过单元界面的对流通量。而施主—受主格式中不同相的界面的方向为水平或者竖直,通量值根据界面的方向及其运动,利用迎风、下风或者两者结合的方法获得。下页图2为两种界面插值格式的对比。
1.3 船体运动
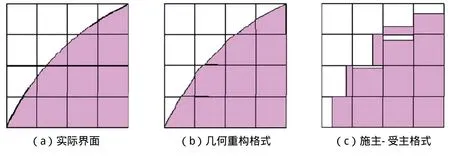
图2 VOF界面插值格式对比
在惯性坐标系中,物体所受到的合力、合力矩,由作用在模型边界上的压力(矩)和剪切力(矩)组成的合力(矩)作用在刚体上,计算出的力和力矩则用来计算模型质心的平动和转动。CFD 根据迭代运算的模型运动来移动网格上的节点,船模可通过计算得到船体表面的受力(矩),根据受力(矩)来调整船体姿态。
延迟函数应用在由于流体流动和重力产生的作用在模型上的力、力矩。释放时间是指在计算开始前的一小段允许流体流动初始化的时间,其长短取决于模型网格的数量等因素。在释放时间内,在流场启动的瞬间,模型周围的压力场与速度场会发生剧烈变化,作用在模型上的力和力矩会使模型产生大幅振动,称为瞬时效应,而应用于力和力矩的延迟时间是为减缓这种瞬时效应[8]。
2 计算模型
计算船模长5.2 m,考虑到船舶的直航运动以及船体严格的对称性,为减小计算量又不影响精度,只对半船模型进行数值模拟,中纵剖面采用对称面边界条件。为保证计算域的进口、出口处流动均为定常状态,计算域的进口、出口分别为船长的2倍、5倍,计算域底部和顶部分别为船长的2.5倍与1.5倍,同时对主体与片体的首部、尾部,水线面,喷水推进器入口进行加密,并设置船行波加密区向靠近船体的方向逐步加密,有利于捕捉兴波及船首尾压力分布,整个计算域网格节点总数为700万,其中流域及进口流道内网格500万,转定子域网格200万,如图3-图5所示。
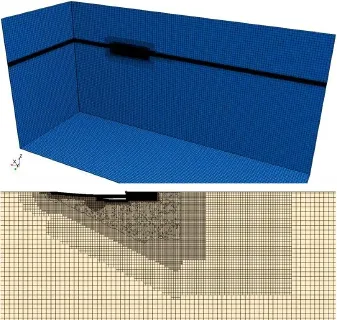
图3 计算区域示意图

图4 船体附近及表面网格
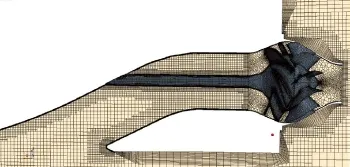
图5 喷水推进器网格
计算中采用有限体积法离散动量方程,采用VOF 方法对自由液面进行捕捉,湍流模型选择标准k-ε模型,压力—速度采用 SIMPLE方法进行迭代求解。动量方程中的瞬态项采用二阶隐格式差分格式,对流项和扩散项的离散都采用二阶迎风差分法。
3 喷水推进三体船阻力数值模拟研究
首先对设计吃水,固定姿态下的船模阻力进行数值计算,再通过6DOF Motion运动模型,释放船模升沉与纵倾两个自由度。因船体表面受力,姿态会进行相应调整,计算实现力的平衡后,船体姿态达到稳定状态。喷水推进三体船阻力数值模拟时,对进口流道的开口进行封闭,与试验状态一致,排除进口流道的影响。
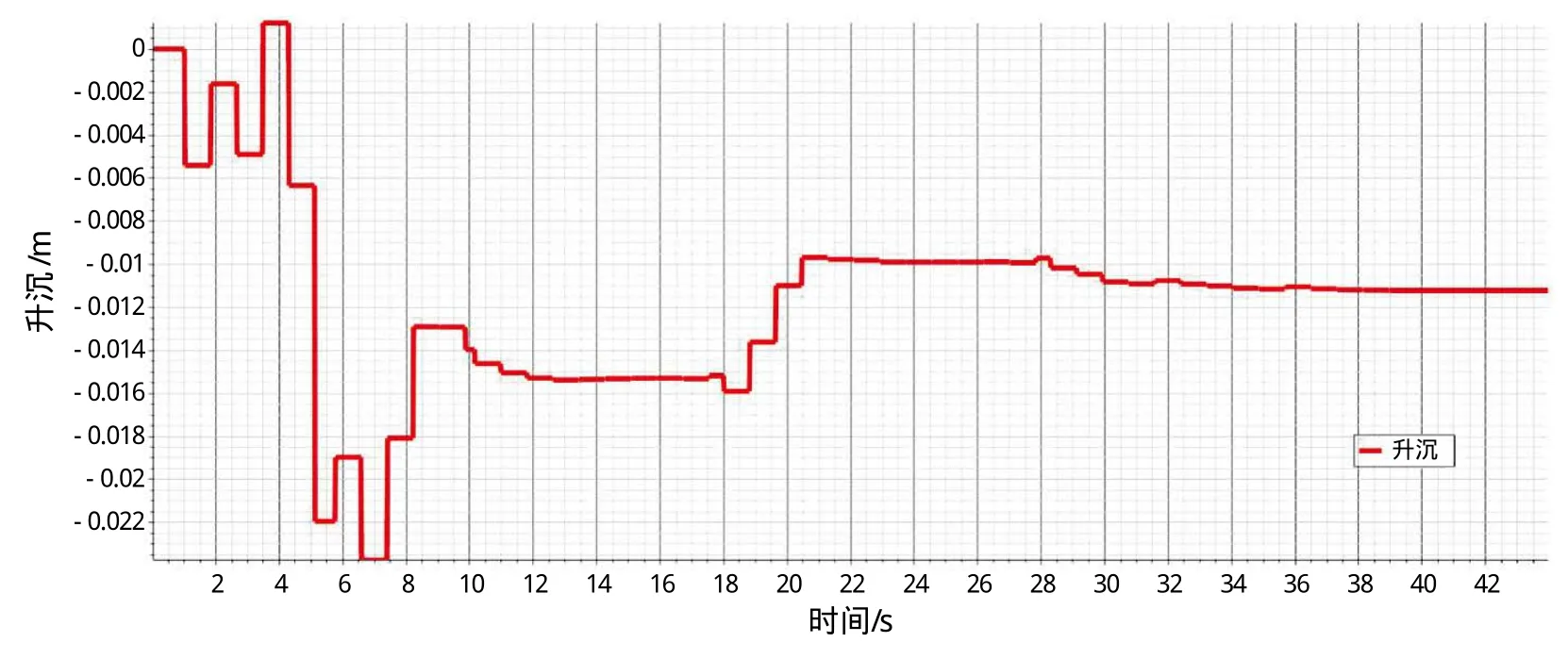
图6 升沉随时间变化曲线
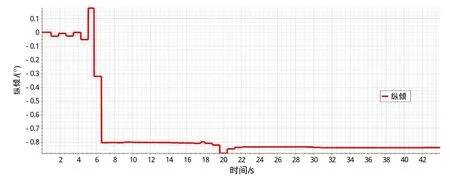
图7 纵倾随时间的变化曲线
对于喷水推进三体船,其姿态(纵倾与升沉)随着傅汝德数的增加而变化,这种变化对引起湿表面积变化,进而影响摩擦阻力,对船体兴波阻力也会产生一定的影响。
计算中为了提升对姿态的模拟精度,相对于初始网格(网格一)针对性的在船体尾部区域,以及船体设置船行波加密区向靠近船体的方向逐步加密(网格二),有利于捕捉兴波及船首尾压力分布。对比升沉与纵倾数值模拟与试验,可以看出网格二对船体姿态的数值模拟更接近试验值,反应在总阻力的计算上更接近试验值,误差在8%~9%。

图8 网格二的加密区域示意图
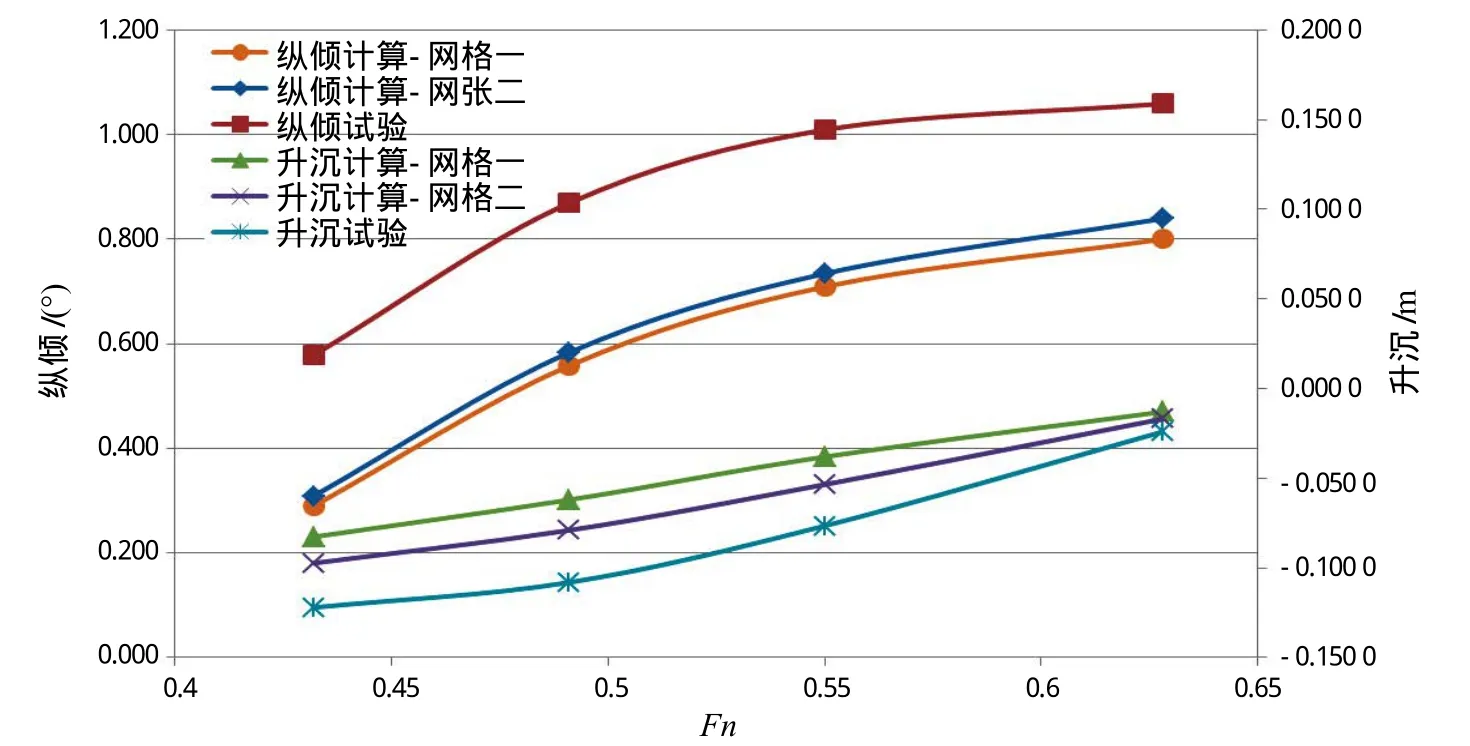
图9 两种网格喷水推进三体船数值模拟姿态对比
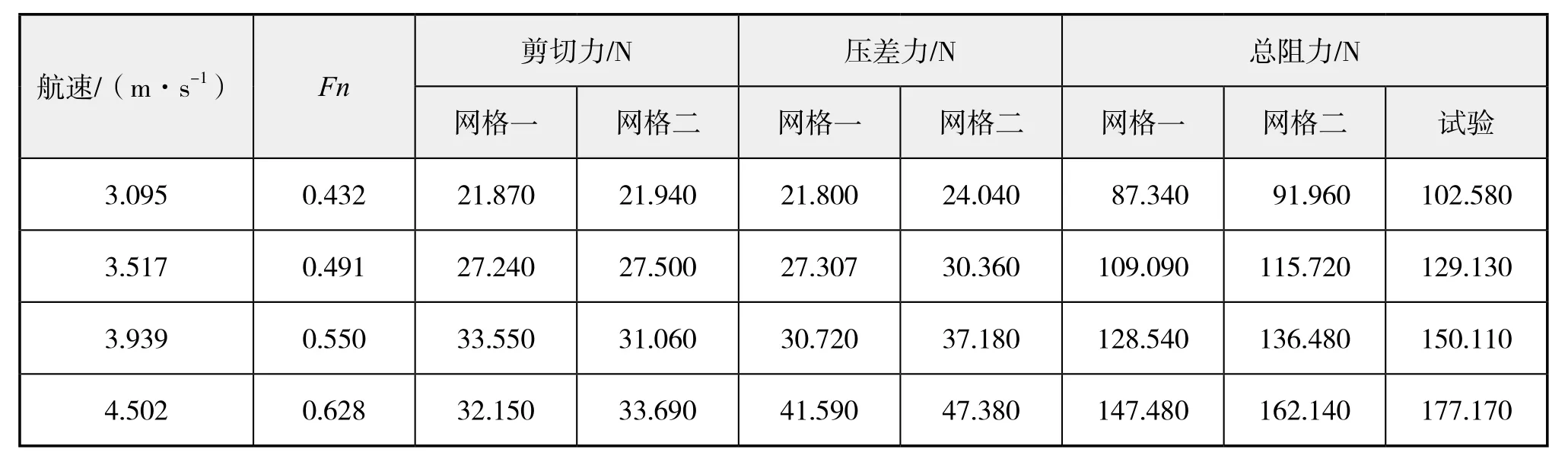
表1 两种网格喷水推进三体船阻力计算对比
为验证是否由姿态误差引起的总阻力误差,计算4.502 m/s 航速下,强制船体姿态与试验值,计算得到总阻力171.6 N,相比于试验值177.17 N,误差3.17%,达到比较好的模拟精度。提升喷水推进三体船阻力的重要内容,还需对姿态的准确模拟。
4 喷水推进三体船自航数值模拟研究
对设计吃水、设计航速工况,喷水推进三体船自航数值模拟,船模的纵倾与升沉姿态设置为自航试验测量值。由于船模自航试验采用的是替代泵,本研究计算中调整喷水推进器的转速,满足喷口流量与试验流量相等,图10与图11分别为初始状态水线与计算得到的自航状态下自由液面与推进器喷射流。
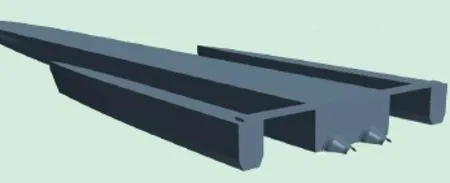
图10 初始状态水线
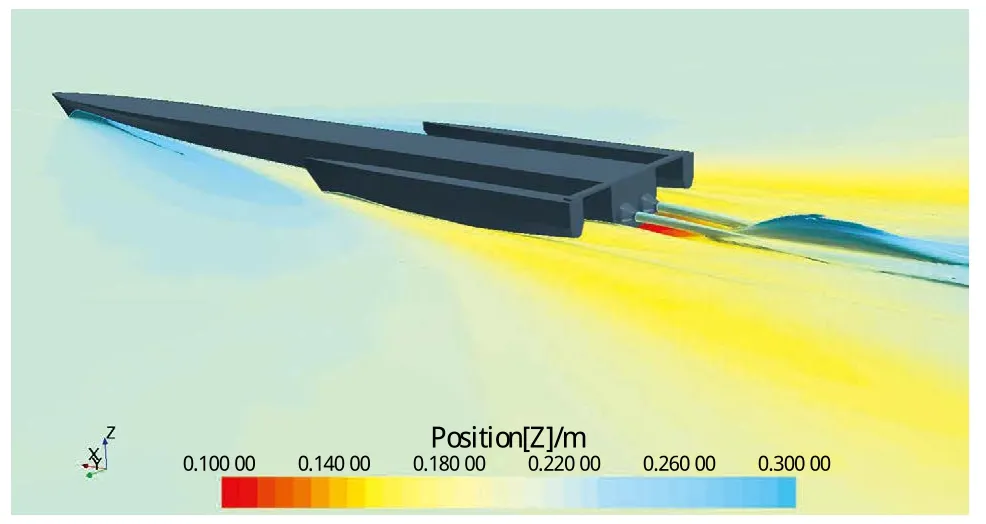
图11 自航状态下自由液面与推进器喷射流
由于喷水推进器的推力由叶轮、进水流道上的力等共同组成,船模试验无法直接测量,一般采用动量通量法获得。图12为喷水推进装置水动力模型的控制体,喷水推进器的推力TJX通过计算进口(1A站)和出口(6站)流量的动量差得到。进口获流区的确定是计算喷水推进器推力的重要步骤,通常定义为进口流道入口前一倍名义直径的剖面处的上游来流被吸入流道的部分,边界层被吸入流道的部分对推进器效率有显著的影响。Cm1为进口获流区的动量影响系数,由边界层速度、压力测量或数值模拟分析得到。表2为数值模拟得到的推进器表面力积分与模型试验进出口动量差计算得到的推力对比,两者误差5.2%。与船模试验相比,数值模拟可以较为精确地得到各部件上的受力,同时也可以得到喷水推进的流场分布。
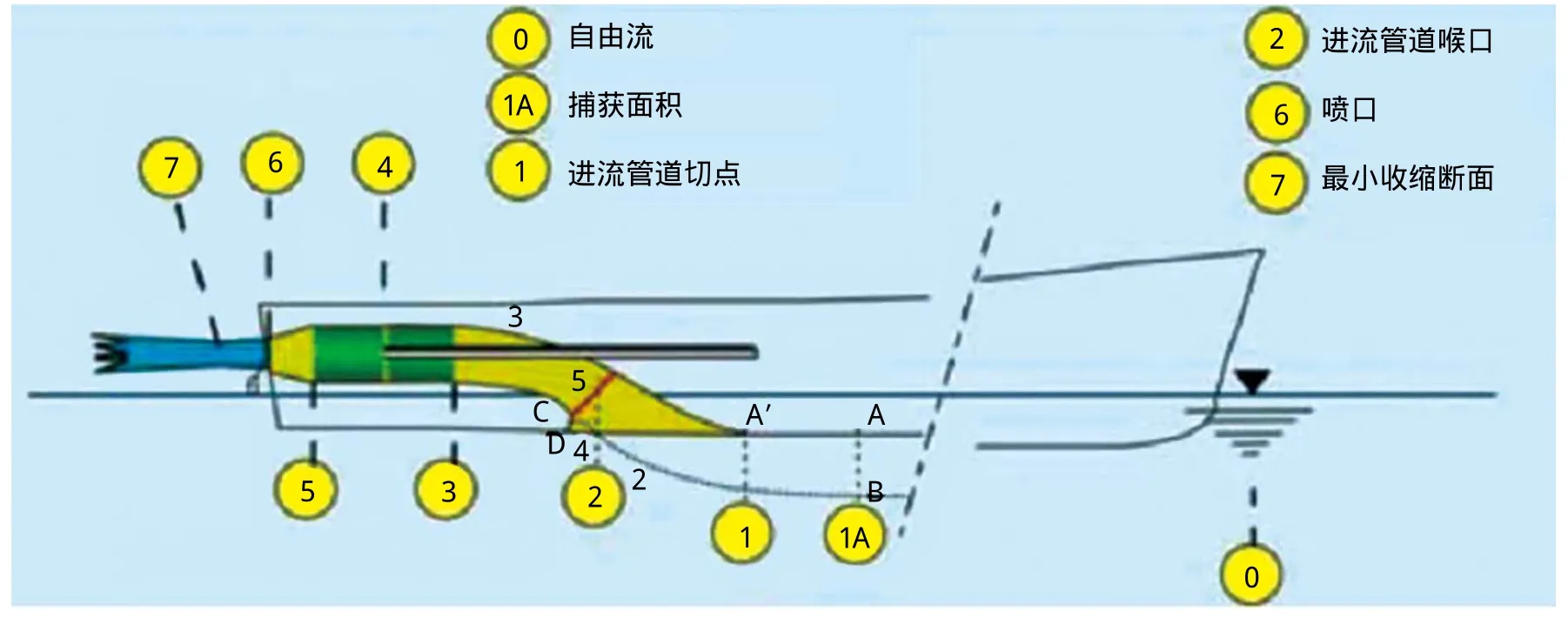
图12 喷水推进装置水动力模型的控制体

表2 数值模拟得到的推进器推力与进出口动量差计算得到的推力
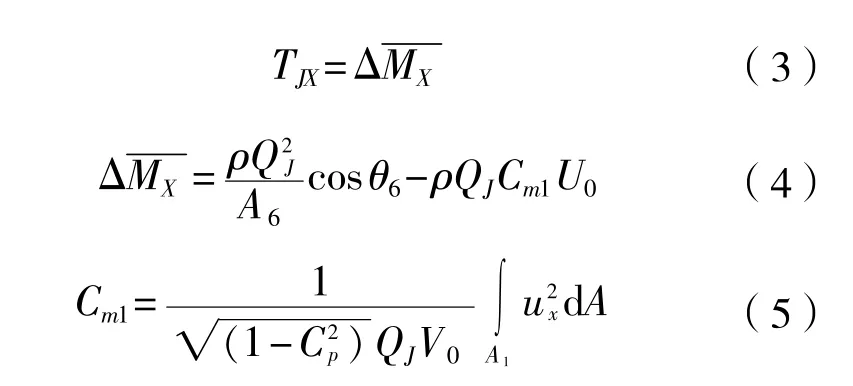
表3为调整姿态与未调整姿态两个状态下推进泵性能对比,下页图13为两个状态下的推进泵入口速度分布。船体边界层及泵抽吸作用对泵前方进流产生影响,带来较大的不均匀度,船体纵倾升沉变化也增加了不均匀度。在相同转速下,调整姿态后推进泵的扬程及力矩都略有增大,效率有所下降。
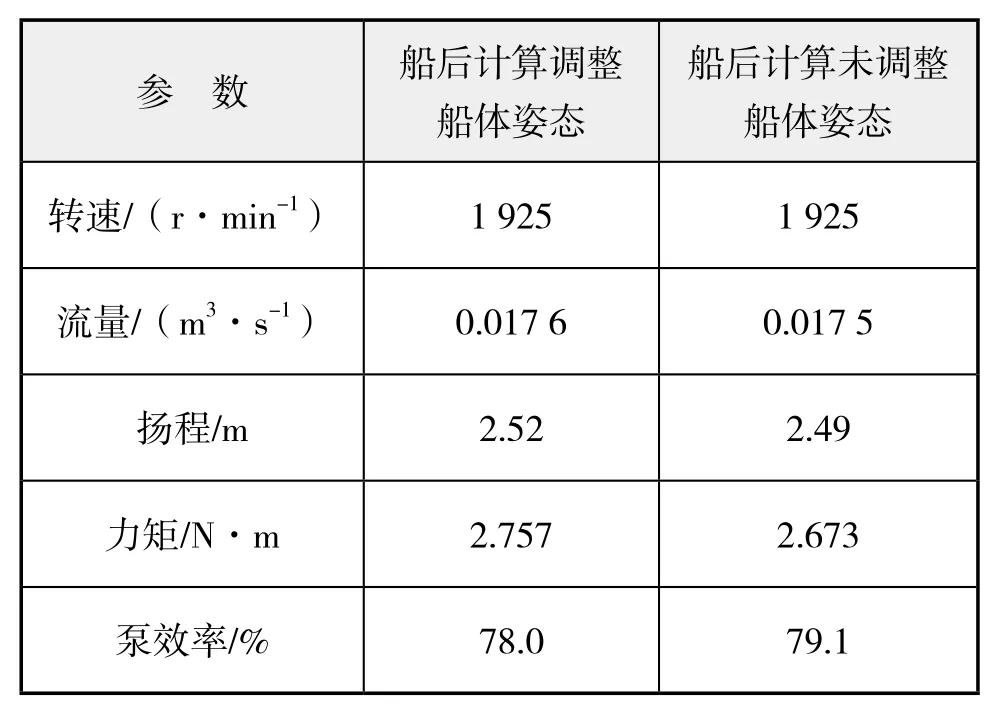
表3 调整姿态(左)和未调整船体姿态(右)推进泵性能对比

图13 调整姿态(左)和未调整船体姿态(右)推进泵入口速度对比
5 结 论
(1)本文基于STAR CCM+软件,采用6DOF Motion运动模型,对包含纵倾与升沉两个自由度的喷水推进三体船模型阻力进行数值模拟,并与模型阻力试验进行对比,该数值模拟方法可以实现模型的多自由度运动,操作便捷,对需要考虑姿态影响的高速舰船快速性预报具有重要的意义;
(2)对于喷水推进三体船,其姿态(纵倾与升沉)随着傅汝德数的增加而变化,这种变化对引起湿表面积变化,进而影响摩擦阻力,船体兴波阻力以及会产生一定的影响,对姿态的准确模拟提升喷水推进三体船阻力模拟精度的重要部分;
(3)在同一航速下的船模自航试验中,船模姿态与阻力试验略有变化,其中自航状态下船模升沉略大于拖模阻力试验状态,主要原因是自航时喷水推进器抽吸作用使改变船底,尤其是尾部的压力分布;
(4)采用数值模拟方法对设计吃水、设计航速工况,喷水推进三体船自航开展定常数值模拟,船模的纵倾与升沉姿态设置为自航试验测量值,数值模拟得到的推进器表面力积分与模型试验进出口动量差计算得到的推力对比,二者误差5.2%,该模型试验证实了数值计算的可信性和有效性。
