约束阻尼结构阻尼效果的有限元预测方法研究

伍先俊

(中国科学院 声学研究所，北京 100190)

机械系统振动消除的方法除减小源振动外，还有隔振和阻尼消振。阻尼消振是在结构覆盖阻尼层来约束结构振动，使得结构振动能量转换为阻尼材料变形的热能，因而消耗掉振动能量的方法。阻尼消振技术在汽车、飞机、铁路运输、船舶中都有应用，特别是结构的共振区，阻尼材料的贴覆能够极大减小振动，降低噪声。

常用约束阻尼结构，是将黏弹性阻尼材料粘合在本体金属板和刚度较大的约束层（通常是金属板）之间，当结构弯曲变形时，本体金属板与约束层产生相对滑移，黏弹性阻尼材料产生剪切应变使一部分机械能损耗的结构。阻尼消振结构有无约束面板的阻尼消振结构和含约束面板的阻尼消振结构，阻尼材料的厚度通常取本体板厚度的2倍左右，选用的约束面板层弹性模量通常远大于阻尼层的弹性模量，厚度为本体金属的1/2～1/4。

对于无约束面板的两层结构和含阻尼面板的三层结构阻尼目前有一些针对梁的简单预报方法[1]，Torvik P J等[2]用复模量描述黏弹材料的本构关系，并用模态应变能法对夹层板进行阻尼振动分析；文献[3]分析提出一种基于GHM模型（由格罗斯曼和哈特(Gross man&Hart,1986)、哈特和莫尔(Hart&Moore，1990)等共同创立的）的有限元计算方法，GHM模型实质是测量了阻尼材料的频域曲线后拟合出阻尼材料的传递函数，文献[4]提出了一种基于GHM模型的有限元理论实现方法，目前的主流商业软件对谐波分析的阻尼处理还是基于复模量的理论，文献[5]根据复模量的理论对多层阻尼圆板的损耗因子进行了分析，选取它们的倒数和为目标函数进行有限元优化设计，不考虑自然频率的导数和对于宽带激励不太适用。本文将对采用有限元法的阻尼因子计算法进行研究，基于模态应变能提出一种新的复合阻尼的快速计算方法，同时结合统计能量分析理论提出一种不同的结构阻尼优化目标函数，并提出基于该函数的有限元优化设计方法。通过经典算例的仿真讨论，验证了基于模态应变能的阻尼计算方法的正确性。对某含约束面板的阻尼层厚度进行了优化设计，最后根据谐波响应分析验证了基于新的阻尼效果评价函数的优化计算的合理性。

1 复杂结构有限元计算理论和步骤

对阻尼结构的阻尼效果分析有谐波分析法和模态分析法，其中谐波分析法可以将阻尼参数代入谐波计算中，直接获得有阻尼响应，是精确的方法。但是谐波计算需要进行整体结构所有自由度的响应，计算耗时长，不适于优化分析。另外一种方法是基于模态应变能的阻尼计算方法，即先计算出各阶模态，通过材料参数和模态变形能计算获得各阶模态阻尼，这种方法比谐波分析计算量小很多。下面将先介绍谐波分析矩阵阻尼模型，然后给出基于模态应变能的阻尼计算方法。

1.1 谐波分析阻尼模型

对于谐波分析的响应，阻尼矩阵可以写为[6]

式中：符号含义如下：[C]结构总阻尼矩阵；α阻尼质量乘子，[M]质量矩阵，β阻尼刚度乘子，g常量结构阻尼因子，Ω激励频率，[K]刚度矩阵，Nm有阻尼材料个数，gj对应于材料j的常量结构阻尼因子，[Kj]基于材料的刚度矩阵，Ne具有阻尼输入的单元，[Ck]单元阻尼矩阵，Ng有科式或者陀螺阻尼的单元个数，[Gl]科式或者陀螺阻尼矩阵（科式或者陀螺阻尼在一般平动结构中不存在，所以本文不予考虑）。

谐波响应分析的方法有完全谐波分析、缩减谐波分析、模态叠加谐波分析和QR阻尼模态叠加分析法。在多种材料的结构谐波响应分析中，要求计算支持配比不同材料的βj，gj和Ck，才可以考虑不同材料阻尼对结构响应的影响，对以上阻尼都支持的有完全谐波分析法或者QR阻尼模态叠加分析法。

完全谐波分析法计算量比较大，QR阻尼模态叠加分析法可以减小计算量，因此本文采用后一方法。

根据动力学方程

对于QR阻尼模态叠加分析法，[K]、[C]可以是非角对称矩阵，QR阻尼模态叠加分析法将[K]矩阵重新排列分出对称部分和非对称部分，通过略去[C]矩阵和[K]矩阵的非对称部分，求得特征值和特征向量，通过以下公式进行坐标变换

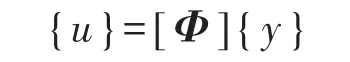
[Φ]为对质量归一化模态振型向量矩阵，{y}为模态坐标，通过以上公式可获得以下式子

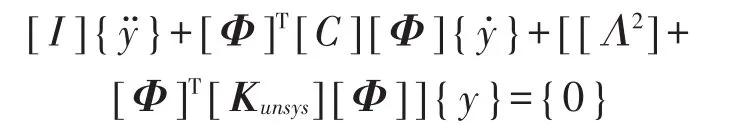
尽管 [Φ]T[C][Φ]和 [Φ]T[Kunsys][Φ]为对角阵，但是模态坐标数目得到减少，计算量得到降低。[Λ2]为对角特征值平方，[Kunsys]为刚度矩阵非对称部分。

1.2 模态阻尼计算

对于具有多种材料，各材料阻尼因子不相同，可以采用基于变形能计算出一个有效模态阻尼因子，在扩展模态时计算单元结果(采用APDL命令MXPAND,NMODE,FREQB,FREQE,Elcalc,SIGNIF，而Elcalc取1表示计算单元结果)

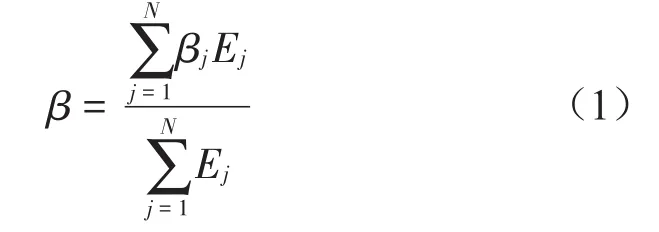
其中：N为材料个数，βj为材料阻尼因子，Ej为对应材料j的模态变形能，Ej={φi}[Kj]{φi} ，{φi}为振型函数，[Kj]对应于材料j的刚度矩阵。

1.3 阻尼评价函数

本文基于统计能量分析的理论，得出一种针对宽带激励的阻尼情形，比较适用于通用场合。受随机激励单自由度振动物体的振速写为[7]

其中：Sf为输入力自功率谱，ωi为单自由振子模态频率，M为被分析结构质量，ηi为单自由振子模态阻尼损耗因子ηi。

多阶模态为多个振动物体，其总的响应为

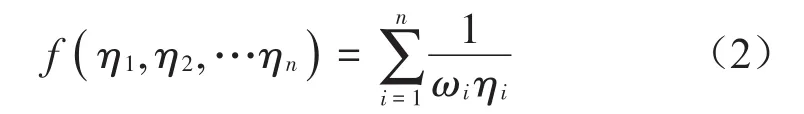
对于多自由度系统，ωi为各模态频率，ηi为模态阻尼损耗因子ηi。

该值越小阻尼效果越好，这种评价与过去的各模态阻尼平均或者倒数和都不相同[5]。

1.4 有限元计算关键过程

有限元分析采用单层实体壳单元代替梁单元，中间层采用实体壳单元，覆盖层采用面壳体单元。各部分单元类型、材料类型、阻尼设置的APDL命令见表1。

Solsh190为3-D8节点实体壳单元，是一种看上去象实体的壳单元，可以模拟从薄到中等厚度的壳结构，薄壳结构无需抽中面，直接划分单元，只需一层Solid-shell单元，并能保证精度。

建立有限元模型，计算模态频率，并扩展获得模态能量值：

2 阻尼计算方法和结果讨论

2.1 对于单层梁计算结果的讨论

图1 自由阻尼约束层示意图

对于两层阻尼结构，损耗因子解析计算式为

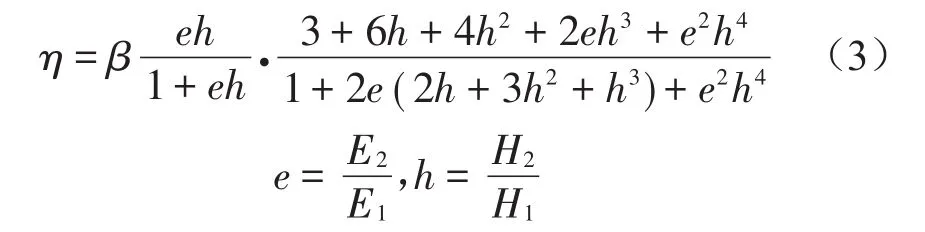
算例：模型基础层采用长0.5 m，截面积为H×B=7 mm×7 mm的铝梁，阻尼材料厚度分别从0.002变化到0.01，阻尼材料弹性模量7×106，密度1 000，泊松比0.4，结构阻尼因子1，两端自由。（为了只比较约束方向模态阻尼，因此约束梁非弯曲方向振动。）

表2是对一个梁结构第1阶模态采用有限元方法和解析方法计算对比，两层阻尼梁解析方法忽略了材料泊松比、梁宽度以及阻尼层质量的影响，在约束层厚度增大时计算误差增大。

有限元计算阻尼层厚度大的结构阻尼因子与解析法差别较大，因此工程中使用解析式（3）需要格外注意。

2.2 对于含约束面板三层阻尼梁计算结果讨论

对于含约束的三层阻尼结构如下

图2 约束阻尼层示意图

表1 各部分单元类型

对于三层梁结构，有以下解析计算公式

对于两端自由梁自然频率计算如下

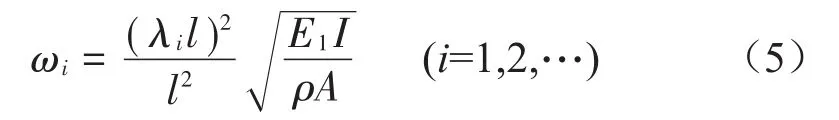
对于两端自由梁，有λ1l=4.73，λ2l=7.85，…λil≈(2i+1)π/2，ρ为梁材料密度，A为梁截面积，I

模型基础层采用长0.5 m，截面为H×B=7 mm×7 mm的铝梁，阻尼材料厚度0.003，阻尼材料弹性模量7×106Pa，密度1 000 kg/m3，泊松比0.4，其结构阻尼因子为1，两端自由，约束层为钢，厚度0.000 5。（为了只比较约束方向模态阻尼，因此约束梁非弯曲方向振动。）

由于约束阻尼层与波长有关系，所以计算前5阶模态（公式（4）计算的模态频率为：147.08 Hz，364.29 Hz，697.31 Hz，1 136.1 Hz，1 680.2 Hz）阻尼大小对比，表3是对一个含约束面板三层阻尼梁结构采用解析法和有限元法的计算结果对比。

有限元计算高阶模态的阻尼因子与解析法差别较大，因此工程中使用解析式（4）需要格外注意。

为了验证有限元计算结果的正确性，采用另外一种方法获得阻尼因子作为验证。即类似于通过实验获得传递函数曲线，通过传递函数曲线辨识阻尼的方法。对于集中点力情况同时计算谐波响应，从而获得传递函数曲线。取距离梁中部0.06 m的位置计算加速度传递函数，传递函数曲线见图3。图中给出了用最小二乘法[8]与以及原始计算获得的传递函数实部和虚部的对比。

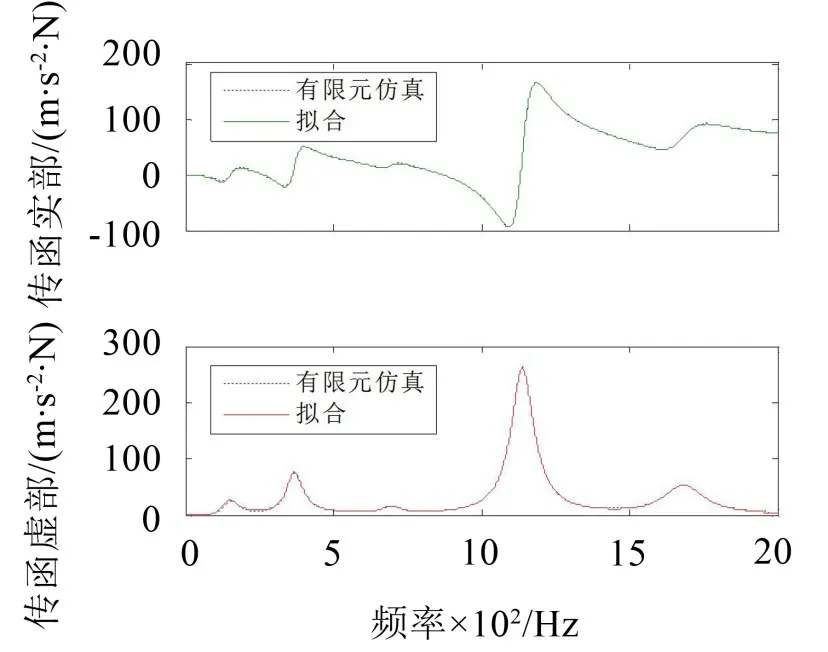
图3 计算获得传递函数和最小二乘拟合传递函数对比

表2 解析方法和有限元计算方法对比

表3 解析方法和有限元计算方法对比

采用最小二乘法迭代法[8]识别出模态频率、阻尼因子和解析解计算的对应数值见表4，可以看出采用有限元传递函数辨识出的各阶模态频率与解析解符合很好，同时各阶模态的阻尼与采用有限元及公式（1）计算结果符合很好，因此验证了采用有限元及公式（1）计算结果的正确性。

说明模态分析得到阻尼与谐波分析得到的阻尼比是对应的，验证了分析结果的正确性。

2.3 板的计算结果和优化

具体优化方法参考文献[9]。

优化解：hd1=0.001，hd2=0.000 69，mas=1.595 5 kg，rs=0.396。为了检验模态阻尼计算结果的正确性，采用完全谐波响应计算优化结果与非优化结果响应曲线对比。

hd1=0.001，hd2=0.000 69，随机取5个点激励，对平板平均速度做平均，优化前后响应谱对比如下图4所示。

表4 传递函数分析辨识获得各阶模态频率和阻尼因子

对一个平板进行优化设计，由于平板模型没有解析方法可以计算，本文先基于模态应变能的阻尼计算方法进行优化设计，然后采用完全谐波分析法进行验证。铝板四端固支，铝平板尺寸：0.5 m×0.5 m×0.007 m，阻尼材料弹性模量7×106Pa，密度1 000，泊松比0.4，其结构阻尼因子为1，约束层为钢。

初始厚度为：APDL设计变量为阻尼层厚度hd1，约束层钢板厚度hd2；阻尼层和约束板总质量限制条件为小于1.6 kg，即以下APDL代码中的状态变量mas小于1.6，以下APDL的目标函数为rs。初始设计hd1=0.002 5 m，hd2=0.000 5 m，而初始设计目标值rs=0.486；

对于优化计算，关键优化代码如下，定义两个优化变量：

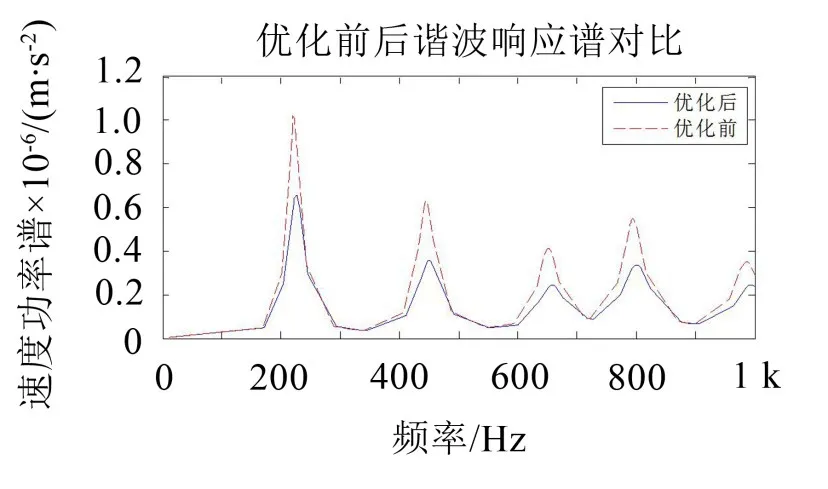
图4 约束阻尼层平板优化前后谐波响应谱对比

从图4可以看出，通过合理分配阻尼板约束层和非约束层厚度，目标值获得了1 dB左右的降噪效果。计算两条曲线下的阴影面积，面积相比按分贝取对数，结果为减振1.1 dB，这与目标函数的变化基本对应，说明采用简化方法的合理性。但是采用简化方法优化计算时长有大幅度降低：一次完整谐波法需要时长80 s；采用模态分析法计算阻尼效果评价函数法需要时长18 s，节省时间量为77.5%；预计对于复杂大模型的计算，优化后速度可提高更多。

3 结语

本文进行了一种基于有限元的阻尼因子计算方法，提出总响应最小的模态阻尼优化计算方法，对三层平板阻尼铺设进行了计算，并采用谐波响应对优化结果的准确性进行了检验。该方法基于商业软件ANSYS提出，具有比较好的工程可操作性，可供实际阻尼优化设计参考。