基于双树复小波变换与引导滤波的红外与可见光图像融合算法*

齐海生，荣传振，肖力铭，岳振军

（陆军工程大学，江苏 南京210007）

0 引 言

图像融合是将多传感器采集的同一场景的图像进行融合，取得信息互补的过程。其中，红外与可见光的融合近年来受到广泛关注，在军事领域起到了非常重要的作用[1]。红外图像成像主要是利用红外热像仪成像获得低光照条件下或者有障碍遮挡的物体的图像，具有良好的探测性能，但红外成像对比度低、纹理细节信息缺失。可见光图像由可见光传感器成像，具有较高的对比度和丰富的纹理细节信息，有利于人眼对场景的认知，但在光照较差或有障碍物遮挡等条件下所成图像效果较差。把红外图像与可见光图像进行有效融合，既能突出红外目标信息，又可以得到可见光图像的高分辨率细节信息，因此被广泛应用于计算机视觉、航天学及军事等领域。

近年来，基于变换域的图像融合方法成为研究热点，寻找适合红外与可见光图像融合的多尺度分解与重构方法成为一个重要的研究方向。小波变换因其多分辨特性能够捕捉信息的奇异点，成为最常见的变换域工具。但是，小波变换方向选择性少，会导致目标边缘不清晰，因此出现了各类改良小波，如脊波变换[2]、曲波变换[3]以及轮廓波变换[4]等。这些改进改善了图像融合效果，但都存在缺憾，如有的不能检测曲线奇异，有的冗余度高、计算复杂，有的不具有平移不变性，融合图像存在振铃现象。近年，在小波变换的基础上发展的双树复小波变换[5]，不仅保留了小波的时频分析特性，还具有近似的平移不变性、多方向选择性（6个方向）以及有限的数据冗余，且计算效率较高，重构效率好，成为当前应用比较广泛的工具。

在红外与可见光图像融合中，还需要充分考虑提取图像显著信息的空间一致性，否则融合图像会出现光影或者重影现象。Li[6]等人提出了一种基于引导滤波的图像融合方法，有效解决了空间一致性问题，但仍存在问题：（1）生成的显著图不能很好地表示图像中的视觉显著特征；（2）图像分解方向单一，不能全方位体现图像各方向的特征。

为此，本文提出了一种基于双树复小波变换和引导滤波器的红外与可见光图像融合算法，对源图像进行分解后，低频子带采用一种改进的基于图像区域能量和的融合规则进行融合，高频子带则结合引导滤波特性，设计基于改进的区域能量和的融合规则，并通过实验验证了算法的优越性。

1 相关理论

1.1 双树复小波变换原理

kingsbury提出的双树复小波变换（DTCWT），相比于离散小波变换，具有优秀的方向选择性、良好的平移不变性、有限的数据冗余、高效的计算效率以及优良的重构效果等优点，从而被广泛应用于各种图像处理工作[7]。DTCWT使用两个单独的离散小波树，其中一路的小波变换作为实部，另一路小波变换作为虚部。两个分解树（树A和树B）平行，假如树A给出实部，树B则定义为虚部。图1为DTCWT的分解示意图。

图1 双树复小波变换

两棵树分别作用于图像的行上和列上，产生双树结构。每一级分解时得到两个低频近似子带分别记作A(j+1,1)和A(j+1,2),同时得到6个不同方向（±15°，±45°，±75°）的高频子带D(j+1,m)，m=1，…，6。该方法比离散小波变换多了3个方向，可提高图像分解与重构的精度，并能够保留图像的细节信息。无论二维双树复小波变换分解层数是多少，总体冗余都是4∶1.

1.2 引导滤波

图像引导滤波器[8]是一种局部线性滤波器。与传统的滤波器相比，图像引导滤波器在保持图像边缘梯度的同时，能够增强图像的细节信息，保留输入图像的整体特征，被广泛应用于图像去噪、图像传输和图像融合。

假设引导滤波器的引导图像为I，输入图像为p，输出图像为q，则在以k为中心、r为半径的窗口Wk中，输出图像与引导图像存在以下线性关系：

式中ak、bk为窗口的线性系数，均为常数，i、k为像素点坐标。从式（1）可以看出， Iaq ∇=∇ ，保证了输出图像q与引导图像I的边缘一致性。下一步是求出线性函数的系数，也就是线性回归，即希望拟合函数的输出值与真实值p之间的差距最小，即式（2）最小：

式中ε是为了防止系数过大而定义的正则化参数。利用最小二乘法对求解式（2），可得出ak、bk的最优解：

uk是引导图像I在窗口中的平均值，σ2k是I在窗口wk中的方差，|w|是窗口wk中像素的数量，p-k是待滤波图像p在窗口wk中的像素均值。对于整幅图像，计算出每个包含像素点i的窗口内的qi值，得到最终的滤波输出图像为：

2 融合规则

2.1 基于改进的区域拉普拉斯能量和的低频融合规则

多尺度变换域的低频系数中包含图像的大部分信息和能量，因此低频系数融合规则的选取非常重要。拉普拉斯能量和（SML）[9-10]反映了图像的边缘特征信息，一定程度上能恰当反映图像的客观情况，但还存在问题：只在水平和垂直方向上计算每个像素点的变步长拉普拉斯能量值，未考虑对角方向。为此，本文采用一种改进的拉普拉斯能量和选取方法，并据此选择图像的低频系数，以获得更好的图像融合效果。

其中，改进的区域拉普拉斯能量和定义为：

其中：

式中w(a,b)为权值矩阵，定义为：

从而，根据该改进方法的低频融合规则：

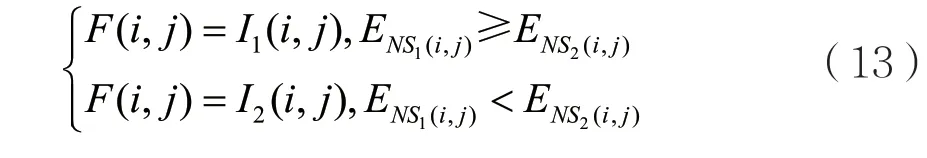
其中，I1(i, j)、I2(i, j)分别为两幅图像的低频分解系数，ENS1(i,j)、ENS2(i,j)分别为两幅图像改进的拉普拉斯能量和，F(i, j)为低频融合系数。

2.2 基于引导滤波的高频系数融合规则

人类视觉系统对边缘、方向以及纹理等比较敏感，基于区域能量的规则可以满足这一要求。因此，本文采用同低频系数相同的方法得到高频系数的加权矩阵。但是，图像中的噪声主要集中在高频部分。为了有效抑制噪声对融合效果的影响，本文应用引导滤波优化高频系数加权矩阵，使得亮度相近的相邻像素值也具有相近的权重，从而满足空间一致性。

首先利用式（6）求取高频系数区域能量，再利用绝对值取大原则得到高频系数加权映射矩阵，最后通过式（14）优化高频系数加权矩阵。

r为窗口半径；Snk,l为第n幅图像的k尺度l方向的加权映射矩阵，作为引导滤波的输入；Cnk,l为第n幅图像的k尺度l方向的系数矩阵，作为引导滤波的引导图；Gr,ε为引导滤波函数。

从而，高频系数的重构可表示为：

3 融合步骤的设定

本文融合采用如下规则：

（1）利用双树复小波变换将源图像分解为低频系数和高频系数；

（2）采用改进的基于区域拉普拉斯能量和取大的融合规则进行低频系数融合；

（3）采用基于区域拉普拉斯能量和取大与引导滤波的方法对高频系数进行融合；

（4）将步骤（2）和步骤（3）中融合后的低频和高频系数，通过逆双树复小波变换重构得到融合图像。

具体过程如图2所示。

图2 基于DTCWT与引导滤波的图像融合流程

4 实验结果与分析

为检验算法特性，对双树复小波变换分解层数进行实验验证，其中低频系数和高频系数均采用本文的方法进行融合，以取得更优的参数，结果如图3、表1所示。由实验结果可知，最优分解层 数为4。

图3 融合图像一

表1 不同分解层数的融合结果对比

在同一种融合策略下，采用不同的变换域对源图像进行分解，通过对融合结果进行比较，说明本文方法的优越性。在不同的变换域下采用不同的融合策略，可以说明本文算法优于其他算法。这部分主要针对红外与可见光图像进行实验比较。具体地，在传统的融合策略（低频取平均值，高频绝对值取大）下选用拉普拉斯金字塔变换（LP）[11]、离散小波变换（DWT）[12]、curvelet变换[13]以及本文方法进行结果比对。为了评价融合结果，采用的客观评价指标有信息熵、互信息量和边缘相似度。

为了使结果更具说服力，对3组红外与可见光图像进行仿真实验，源图像及融合结果如图4～图6 所示。其中，每幅图像中的前两个均为源图像，其余为采用上述算法获得的融合结果。

图5 融合图像三

图6 融合图像四

从3组融合图像来看，4种融合方法均提取到了源图像的互补信息，融合后图像能反映两幅源图像所表达的内容；融合图像中，（c）、（d）图像有明显的块效应，图像整体较为模糊，图像（e）中出现了一些锯齿状纹理，图像（f）的融合效果大大改善，图像自然明亮，对比度适中，区域特征比较明显。

从客观的信息熵[14]、互信息量[15]以及边缘相似度[16]三方面对融合结果进行定量分析，结果如表2所示。

表2 不同算法融合结果对比

从客观评价指标看，本文方法优于传统融合规则下的其他变换域融合方法，能有效保留图像的边缘和轮廓信息，验证了本文算法的有效性。

5 结 语

本文采用基于双树复小波变换与引导滤波的方法对红外和可见光图像进行融合，在融合规则的设定上，图像分解完成后，对低频部分进行基于引导滤波的方法进行融合，高频部分进行基于改进的区域能量和的方法进行融合，并与传统的多尺度分解融合方法进行比较分析。结果表明，本文提出的方法能有效保留源图像的轮廓和边缘信息，主观视觉上融合图像自然清晰，对比度适中，客观评价指标上也优于其他方法。