无线传感器网络基于时空差分阈值Huffman数据压缩

，，

(湖北大学 计算机与信息工程学院，武汉 430062)

0 引言

传感器网络[1]由大量的传感器节点随机部署在空间中组成的，单个节点主要组成模块包括数据采集模块、通信模块、电源管理模块。由于节点的能量、存储、通信距离有限,为了减少节点在数据传输的过程中消耗的能量[2]和节点无休眠的工作消耗的能量，采用了对节点有限时间内自适应采集的数据与数据压缩的方式。该方式不仅减少了相对应数据的传输量[3]，而且减少了节点能量的消耗；此时通过传感器网络中节点不同时刻和不同位置采集的数据具有一定的时空相关性[4]，以及传感器节点对自身采集的数据可以通过硬件功能进行处。然而无线传感器网络中的节点在同一片区域采集的数据具有相对变化较小的特性，对该处理的数据将进行无损压缩[5]，并要求传送的数据(如：温度，湿度)精确到一定程度。本文提出了一种基于时空差分后Huffman的数据无损压缩算法。该方案采用单个节点自身对数据采集和处理，处理后进行编码传输，节点的传输数据大量减少[6]，同时也能将压缩的数据进行还原。因此减少了节点发送的数据量和网络中的通信流量[7]，并延长网络生命。

Steffen[8]提出了一种自适应压缩大型矢量的方案，该方案对节点自身的处理数据要求非常高，然而节点采用的处理方式速度较慢，加大了处理数据的时间，数据不能及时发送，也未达到节约能耗。Ikjune Yoon[9]提出了无线传感器网络能量采集的自适应传感和压缩率选择方案，通过电池的能量情况选择不同的压缩模式。该方案在开始就需要比较对压缩方案进行选择判断，在节点能量较低的情况下采用低压缩率方式，对节点的能量并没有太多的节省。Sunyong Kim[10]提出使用能量回收的无线传感器网络中的数据压缩延长网络寿命,该方案通过簇头对数据进行多级压缩，然而多级压缩过程容易导致树列后节点的能量消耗过快。Francesco Marcelloni[11]提出了一种无线传感器网络监测小节点的高效无损压缩算法，该方案采用的LZW编码这种扩展会产生更高的内存占用，但不会明显影响压缩比，而且对应于较长代码的差异具有非常接近0的概率。

上述文献都考虑到了压缩节点采集的数据，然而并没有真正在将数据量减少的情况下进行无损压缩数据[12]，同时保证数据采集的时效性和数据的无损性。本文通过时空性使用差分器将数据差值，再将差值后的数据与阈值比较后进行Huffman编码，最后节点将无损压缩的数据传递给簇头，再传送给服务器，服务器接收到数据后通过叠加的方式将数据还原。由于服务器是一直供电，当对收到的数据进行还原时并不用考虑服务器的能耗问题，通过实验数据分析，采用差分Huffman编码减小了节点的功耗[13]，同时也提高了数据压缩的比率和网络生命周期,并保证了节点在能量消耗保持相对稳定。

1 数据压缩理论

1.1 数据的时空性

无线传感器网络节点通过传感器采集数据，并通过A/D模型将采集的模拟信号转换成数字信号，节点发送的数据包含节点ID和节点所采集数据(图1)。通过节点采集的数据具有一定的时间相关性，同一节点相邻的两个时刻采集的数据具有一定的关联，当相邻时刻采集的数据不变时，可以减少大量的数据传输；同时，不同的节点间的数据具有一定的空间相关性，当在一定的区域中，不同节点采集的数据具有一定的差异时，根据区域内多个传感器采集的数据进行比较分析，可以将大量一致的数据在矩阵中转换成0后，再进行传输到网关，并可以减少簇头在传输时的数据。此时可以将数据放置在三维空间表示(图2)，节点通过当前时刻的数据与前一时刻的数据进行差值，并将同一簇类节点的数据进行比较，之后采用无损压缩将数据传输给服务器。由于无线传感器网络的数据传输消耗的能量与距离和放大系数有关，传输数据的能量远大于处理数据所用的能量，此时传输数据消耗的能量[14]公式为：

ETX=mEelec+Eamp(m,d)=mEelec+mεdx

(1)

Eelec为采集1bit数据消耗的能量；Eamp为传输时消耗的能量，d表示节点与簇头的距离，ε表示传输时与距离相关的放大倍数；

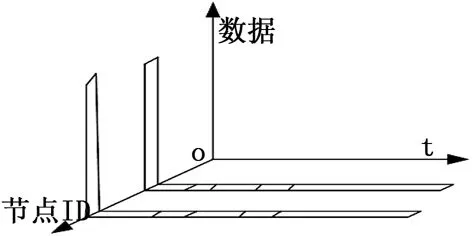
图2 节点的时空性

1.2 一阶差分方程

节点中的每一个传感器采集到的数据不相互影响，通过差分器将现在时刻采集的数据与前一个时刻的数据进行差分(图3)。多个数据同时进行并行处理并获得一个差分值。该差分器的公式为：

yi(n)=xi(n)-xi(n-1)

(2)

而此时xi(n)为单个节点传感器某时刻所采集的数据xi={xi1,xi2,xi3,,,xin},并通过单个节点现在采集的数据与前一时刻xi(n-1)的数据进行差分，并获得yi(n)={yi1,yi2,yi3,,,yin},yi(n)为单个节点所有传感器采集的数据差分后保存的数据；为了保证数据的有效性，同一簇内将对不同的节点进行比较分析，同时消除数据的冗余；这时再将所获得的数据yn进行编码，同时根据yn所产生的数据进行Huffman编码，并确定该值以确定编码长度。

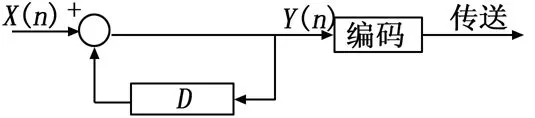
图3 差分器数据模型

此时为单个节点的数据差分，由于多个节点具有多个传感器可以采集多个数据，此文将根据LEACH分层协议[15]，普通的节点将数据传输给簇头，簇头将数据收集后传送给网关，最后在传给服务器。节点将采集的数据转换在矩阵中进行存储，初始数据都为H0(为了方便处理数据已经在服务器接收到数据应为同等大小矩阵，簇内低于规定的矩阵的列数采用零补充，大于列数的簇将舍弃簇内数据差异性很大的节点)。当所有节点部署完毕后并正常工作，第i个节点初次开始采集的数据xi={xi1,xi2,xi3,,,xin}并存储在内部的存储器中并传递给簇头，同时将一个簇内所有节点采集的数据直接传递给簇头，并在簇头中以矩阵H1方式存储，并进行编码传递给网关；此时，每个节点都有了初始的采集数据，而后每一次采集的数据通过与前一时刻采集的数据进行差分(式2)，单个节点差分后的数据为yi(n)，同时簇内有多个节点，并将保存数据存储为Hn。为了保证数据有准确性和数据压缩效率高，并在此设定一个标准的高斯分布(α=0.05)作为数据置信区间的阈值矩阵为HT(图4)，并以此判断差分后的数据是否在阈值范围内；当yi(n)的差值大于阈值，则此时刻节点判断差值大于阈值，节点将重新装载数据xi，同时节点将数据传递给簇头，并重新载入新的节点数据给H1。

图4 数据的存储

而此时的Hn是在某个时刻在一个簇内不同的节点产生的数据并具有一定的空间性，通过于上一时刻的数据差分后，簇头存储的数据可以根据空间性，将矩阵中的数据大部分转换成0，但并不是所有的差分后数据都是0，再次之后对簇头的数据进行数据压缩，这样将大量减少了簇头的数据量，所以将采用时间和空间相结合对数据进行处理。

2 差分后的Huffman数据压缩

2.1 动态Huffman编码

如果基于静态Huffman编码则需要对字符需要两次扫描，而动态Huffman编码是不需要事先构造哈夫曼树和输入扫描符号流；而是一边进行编码，同时开始构造哈夫曼树；这样可以减少处理器消耗的能量和时间。

当初始化编码数时，由于只能对数据流进行一次扫描，所以不能预先知道每一个符号的出现次数和频率。为了对所有符号一致对待，编码树的初始状态只包含一个叶节点，包含符号 NYT(Not Yet Transmitted，尚未传送)，权重值为 0。NYT 是一个逸出码(escape code)，不同于任何一个将要传送的符号。当有一个尚未包含在编码树中的符号需要被编码时，系统就输出 NYT 编码，然后跟着符号的原始表达并重新给予新的编码树。

当输入一个字符时，将会构造一个空的新子树，子树包含NYT符号和新符号的两个节点，并用新的节点取代旧的NYT节点在子树的位置(最初的NYT权重为0)，将旧的NYT取代后，新符号节点的叶节点的权重为1，同时将试图对该父结点执行权重加一的操作。同时，每读取一个字符，首先检查字符是否已经在编码树中；如果不在，则先对空叶结点进行编码，再生成一颗子树，其右分支结点为刚的读入的字符，其左分支结点为新的空叶结点，并用这个子树代替原来的空叶结点；如果在已经编码的树中，则以静态哈夫曼编码的方式进行编码，如图5所示。

图5 动态Huffman编码过程

2.2 时空差分阈值Huffman编码

当节点采集好的数据在自身的内存中具有一定的时效性，通过该内存存储初始的数据作为一个基准，初始时刻的数据直接基于动态Huffman编码进行传输，此后的数据基于前一时刻的数据先进行差分，并存储在矩阵中Hn。对差分后的数据设定一个阈值HT，当进行差分后的数据小于阈值，则节点直接将差分器差分的差值进行编码，如果节点的某一个传感器差分的值大于阈值，则节点将此时的数据直接编码进行传输，并以此数据为基准进行差分，如图6所示。

图6 数据处理过程

为了保证数据传输的没有太多的冗余的数据，每一次数据都要进行差分阈值的比较，而此时采用的阈值使用高斯分布置信区间验证是否能正常通过Hn进行动态Huffman编码。对该差分后的数据进行高斯分布X～N(0，1)的检验思想方式，假设差分后的Hn能通过置信区间，则将数据传输给编码器进行动态Huffman编码；反之，差分后Hn通过不了置信区间，此时，节点将采集到的原始数据进行动态Huffman编码，并将此时刻采集到的源数据压缩后发送给簇头，同时簇头收到数据后，也将采用动态Huffman编码进行传输。然而置信区间往往可以由某参数的显著性水平为α(α=0.05)的检验，得到该参数的置信度为1-α的置信区间[-2,2]，当在置信区间内是，反之。显著性水平α的均值μ的双侧检验出现问题，则高斯分布标准化公式：

(3)

对数据进行差分后减少了大量的数据，在同一区域内分析数据的可靠性之后，并通过动态的Huffman编码对矩阵Hn进行数据压缩，由于每一次的数据都是未知的，通过Huffman编码的动态原则，先编码在调整编码数进行压缩。动态的Huffman编码以默认的概率进行编码，并不断更新元素的概率，从而可以达到高概率出现的分配给小规模的数据流位。

动态Huffman编码是基于动态变化的哈夫曼树,也就是说,对第t+1个字符编码是根据原始数据中前t个字符得到的哈夫曼树来进行的。压缩和解压子程序具有相同的初始化树,每处理完一个字符,压缩和解压方使用相同的算法修改哈夫曼树,因而该方法不需要为解压而保存树的有关信息。压缩和解压一个字符所需的时间与该字符的编码长度成正比,因而该过程可以实时进行。

3 实验仿真

通过Matlab对数据压缩进行处理，为了让实验效果更明显，将采用LEACH协议对节点采集的数据进行压缩，同时引入SINK中继站尽量节省节点的能量。与原有不采用压缩对比，能量消耗相对减少、数据传输效率和网络寿命都相对提高，同时也保证了数据的准确性；并主要分析了WSNs网络的数据传输量，对比网络生命周期等数据；将300个节点随机部署在400 m*400 m的正方形内，BS的坐标为(0,0)。在仿真中，本节通过大量的实验比较同一领域的压缩算法；主要分析WSNs网络寿命和数据传输。WSNs主要参数如表1所示。

通过实验对比分析，当节点采集数据后进行Huffman、动态Huffman、差分动态Huffman三种压缩算法，三种无损压缩算法都对节点的数据进行了压缩，然而前两种算法的压缩效果并未达到理想效果，通过图7可以看出，差分动态Huffman算法在压缩前对数据进行了相对应的融合，在减少了数据的传输同时反而增大了数据量传输，明显可以看出Huffman编码的压缩效果低于差分动态Huffman无损压缩。

图7 三种算法的数据传输

图8呈现了三种算法的能量的消耗，当节点与簇头之间的距离较远时，节点在数据采集后进行数据压缩消耗的能量低于数据传输的能量，当节点采集数据开始时，节点第一次的数据将直接进行动态Huffman编码传输，此后节点通过前一次时刻的数据与现采集的数据进行差分，并将大量的冗余数据抵消，只用将差值后的数据进行动态Huffman编码，再将编码后的数据进行传输。数据传输的数据量越少，则网络消耗的能量就越少。此时整个系统中的能量消耗减少，则总体的剩余能量将相应的减少，图9表示为三种压缩算法的剩余能量对比。图10显示，当采用差分Huffman算法时可以大大减少节点的死亡率并保证了节点的相对稳定性，同时也提高了数据的压缩率，这样将会让整个网络更好地监控该区域的环境。

图8 三种算法的网络能量消耗对比

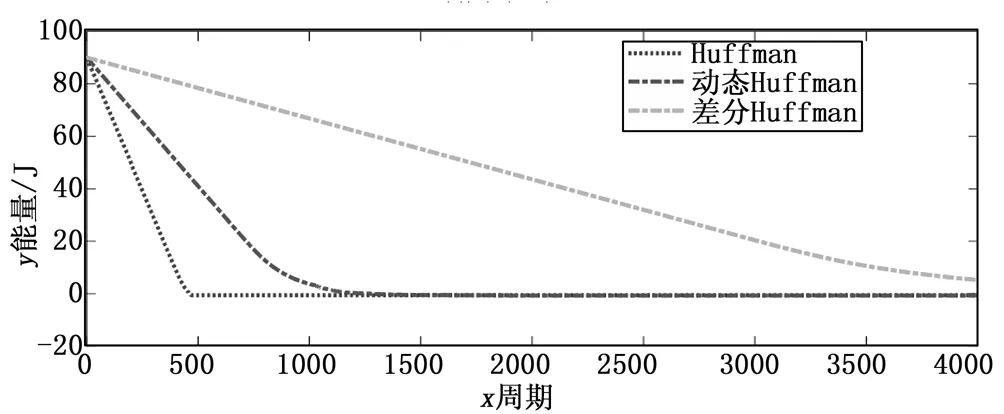
图9 三种算法的网络的剩余能量

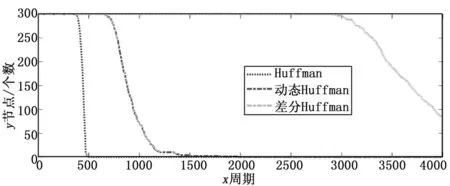
图10 三种算法节点的存活数

在仿真中，为了保证该方案可行性，采用了节点数为100/200/300/400/500个节点部署进行了数据压缩比的分析。通过压缩算法的训练，当节点数越多时，三种算法的压缩率都会提高，而差分Huffman算法的压缩也随之提高。压缩率公式为：

(4)

表2 三种算法的压缩率对比 %

通过表2的数据压缩比率统计当节点数增多时，差分动态Huffman算法的压缩比率是不断增大，传输的数据量相对是不断减小。当直接采用Huffman编码时当节点数增加到某一个值时节点的压缩率将会保持并不在减小，而差分动态Huffman算法确保了节点的数据压缩率、数据的无损性、数据的准确性、节点的节能性，同时保证了网络系统的稳定性。

4 总结

本文主要针对无线传感器网络数据压缩算法进行研究，采用差分器再对数据进行动态Huffman编码。当数据进行减法时将大量的相同数据抵消，只用将差值编码进行传输，极大的节省了数据传输的能量，并将数据传输的准确性也得到了提高，也减少了簇内成员的通信开销，提升了网络的生命周期。然而本文的不足在于没考虑到SINK的运行速度和路径规划。后期将会结合SINK与数据压缩，并提高网络生命周期。