基于压缩感知的遥感成像稀疏重构性能分析

，，，，

(1.空军工程大学，西安 710051； 2.飞行器控制一体化技术重点实验室 中航工业自控所，西安 710065)

0 引言

遥感成像是一种重要的对地信息测量手段，具有平台高、视域广、可连续成像等特点，多年来，其理论与技术在国际上不断得到完善和突破，被广泛应用于环境监测、资源勘探、灾害预报、军事侦察等重要领域。随着时代的发展，信息获取的需求对遥感成像提出了越来越高的要求，使得遥感成像向着多光谱、大视场、高分辨率等方向迅速发展。然而，由此产生的庞大数据量，给数据处理和实时传输造成巨大压力，在很大程度上限制了遥感成像的性能及进一步发展。

压缩感知[1-2](Compressive Sensing, CS)是近年来提出的一种新型信息论，该理论以信号的稀疏性为先验，通过采集远少于信号本身数据量的投影值，然后利用非线性的重构算法精确恢复原始信号。该理论实现了在采样的同时完成数据压缩，能够很好地解决提高采样率和舍弃冗余数据之间的矛盾，在遥感成像领域具有较好的应用前景。信号的稀疏重构[3-4]是压缩感知的核心内容之一，也是压缩感知由理论转化为应用的关键步骤。受稀疏重构算法无法精确求解的限制，当前多数重构算法均采用了近似求解的方式，使得原始图像与重构图像之间存在一定程度的误差。因此，遥感图像稀疏重构性能的优劣直接决定了压缩感知理论能否在遥感成像中的应用。

本文首先针对稀疏重构模型和求解方式，分析了稀疏重构误差的理论来源；接着，针对光学遥感图像分析了图像重构误差产生机理，并给出了图像重构误差的评价指标；最后，通过仿真实验，考察了在不同压缩采样率、不同重构算法下遥感图像重构性能。

1 稀疏重构误差分析

一般地，离散信号x在正交基Ψ上可以稀疏表示为:

x=Ψα

(1)

其中:α为稀疏表示系数，如果系数α中有K个较大或非零值，那么x即为K阶稀疏信号。压缩感知的主要过程是通过一个M×N的测量矩阵Φ对信号进行压缩采样，满足M≪N，得到低维测量值y，即:

y=Φx

(2)

稀疏重构是从压缩数据y恢复原始信号x的过程，也就是:

(3)

理论上，式(3)是一个欠定稀疏优化问题，无法得到精确解析结果，需要针对优化问题寻求近似解法，并在近似求解过程中产生重构误差。目前，稀疏重构算法主要分为两大类：凸优化类算法[5]和贪婪类算法[6]。凸优化算法是将式的l0范数问题转化为l1范数进行求解，即

(4)

同时，在求解过程中，将约束条件转化为惩罚项，构造非约束优化问题，即:

(5)

以Bregman迭算法为例，式(5)的优化求解方法如下。

Bregman算法流程:

输入：测量矩阵Φ，测量值y，稀疏度K；

Step1：定义x和z点之间的Bregman距离为:

Step2：求解优化问题:

考虑l1范数是最接近l0范数的凸函数，因此使用l1范数替代l0范数进行求解是一种常用的方法。然而，这种方法得到的最优解x*是l1范数的优化结果，该结果虽然能够很好地逼近x*→x，但理论上仍然存在一定程度的重构误差。

贪婪算法是根据匹配追踪的思想，迭代地从稀疏字典中选择原子，同时计算相应的表示系数，通过局部优化依次找到最优解，即将式转化为近似求解形式:

(6)

以正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)为例，式(6)的近似求解方法如下。

OMP算法流程:

输入：测量矩阵Φ，测量值y，稀疏度K；

初始化：索引集Γ0=φ，支撑集ΦΓ0=φ，残差值r0=y，迭代次数n=1；

Step1：计算残差与测量矩阵内积gn=ΦTrn-1；

Step3：更新索引集Γn=Γn-1∪{k}，同时更新支撑集ΦΓn=ΦΓn-1∪{φk}；

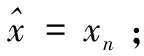
2 图像误差评价指标

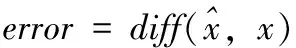
(7)

其中，函数diff(α,β)寻求α与β之间的差别。

(8)

该指标反映了稀疏重构图像对原始图像的逼近程度，PSNR值越大，重构误差越小，重构图像就越接近原始图像。

同时，对于相同图像，稀疏重构误差的大小主要与算法类别和压缩采样率有关。考虑不同算法类别，在凸优化类和贪婪类算法中，各选取两种较为典型的方法进行实现，考察压缩感知稀疏重构对遥感图像质量的影响。其中，凸优化类算法选择内点法[7](Interior Point Method, IPM)和Bregman迭代[8]算法；贪婪类算法选择OMP算法[9-10]和稀疏自适应匹配追踪算法[11](Sparsity Adaptive MP, SAMP)。

定义压缩采样率η为压缩测量过程中，测量次数m与原始图像规模n的比值:

η=m/n

(9)

其中:n=M×N。理论上，压缩采样率越高，对原始图像的信息获取程度越高，稀疏重构结果就越接近原始图像。对所实现的4种典型算法，考察各算法在不同压缩采样率下遥感图像的重构误差。

3 仿真实验分析

针对压缩感知的三个要素，即稀疏表示、压缩测量和稀疏重构，分别进行仿真实验设计。首先，构造离散余弦变换(Discrete Cosine Transform, DCT)基作为稀疏表示基Ψ，针对图尺寸为256×256和1024×1024的遥感图像，分别生成相应大小的DCT稀疏表示基，如图1所示。理论上，不同尺寸的稀疏基对相应尺寸图像的稀疏表示能力相同。

图1 不同尺寸DCT稀疏表示基

其次，构造压缩测量矩阵，选择Toeplitz循环矩阵作为实验测量矩阵，图2显示了一个尺寸为64×256的测量矩阵，其能够对规模是256的信号实现25%的压缩采样率。

图2 Toeplitz循环测量矩阵

最后，分别实现IPM、Bregman、OMP和SAMP 4种稀疏重构算法，完成压缩感知整个过程，并重点评价4种算法下遥感图像的稀疏重构效果。实验数据选取256×256低分辨率均匀场景遥感图像以及1024×1024高分辨率复杂场景遥感图像共50幅，组成图像库进行统计仿真，图3显示了不同类型的遥感图像。

针对每幅图像，分别选取20%、30%、40%和50%的压缩采样率，逐一进行压缩感知并完成不同算法下的稀疏重构。为了更好地显示图像重构误差，选择较低压缩采样率20%，以图3(a)所示遥感图像为例，在4种算法下的重构图像如图4所示。

图4 不同算法下稀疏重构遥感图像

可以看到，在较低压缩采样率下，凸优化类算法(IPM和Bregman)对遥感图像的重构质量总体上优于贪婪类算法(OMP和SAMP)，其重构图像细节更加接近原始图像；而两种贪婪算法重构图像中，对图像细节的还原程度相对较低。这是由于凸优化类算法的优化模型使得结果能够更加接近原始图像，而贪婪类算法则以匹配追踪的方式得到了局部最优解，因此存在相对更大的重构误差。

统计图像库中所有图像在IPM、Bregman、OMP和SAMP四种算法中不同压缩采样率下的算法平均运行时间，其中高分辨率图像截取与低分辨率相同数据量进行时间平均计算，结果如表1所示。结果表明，凸优化类算法较贪婪类算法需要更长的重构时间。其中，在不同压缩采样率下，IPM算法运行时间保持在10 s左右，而Bregman算法随着压缩采样率的提高，运行时间由17.58 s减少到11.83 s，这是由于更多的采样数据加快了算法的迭代收敛速度。相对而言，贪婪类算法的运行时间远低于凸优化类算法，随着采样率的提高，OMP算法的运行 时间由0.64 s增加到3.16 s，而SAMP算法的运行速度更快，在所选择的采样率下，普遍保持在1 s以内。

表1 算法运行时间比较 s

统计图像在不同重构算法和不同压缩采样率下的图像重构误差，计算相应的PSNR值，并降序排列结果，统计结果如图5～图8所示。

图5 IPM算法图像重构PSNR值

图6 Bregman算法图像重构PSNR值

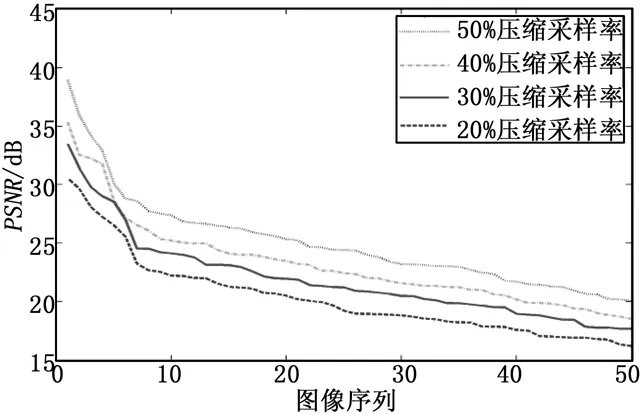
图7 OMP算法图像重构PSNR值

图8 SAMP算法图像重构PSNR值

结果表明，对比4种不同的稀疏重构算法，凸优化类算法对遥感图像的稀疏重构效果整体上优于贪婪类算法。其中，IPM和Bregman算法重构效果较为接近，各压缩采样率下的图像平均PSNR值保持在3 dB以内；OMP算法重构效果相对差，随着压缩采样率的降低，图像重构PSNR值下降较快，SAMP算法优于OMP算法，各压缩采样率下的图像平均PSNR值高约5～6 dB。

总体上，凸优化算法计算精度较高、重构误差小，但计算复杂度较大，当信号规模较大时，数据处理时间相对较长。贪婪算法计算复杂度较低且容易实现，但重构精度不高，在压缩采样率不足时导致图像重构误差较大。

在相同的算法下，图像重构质量随着压缩采样率的增加而提高，表明增加压缩采样率能够很大程度上提高图像重构质量。此外，在较低压缩比20%时，凸优化类算法对遥感图像重构PSNR保持在20 dB以上，而贪婪算法的为15 dB以上，并且通过增加压缩采样率，可以进一步提升稀疏重构性能，在一定程度上验证了稀疏重构在遥感成像中应用的可行性。

4 结论

本文针对压缩感知稀疏重构对遥感图像的影响进行了研究，定量分析了在不同压缩采样率、不同重构算法下的遥感图像稀疏重构效果。结果表明，在所选取的20%、30%、40%和50%的较低压缩采样率下，4种重构算法对遥感图像均能够成功重构，并实现了较好的重构效果。同时，随着采样率的提升，各算法均能够在很大程度上提高图像重构质量。结论成功验证了遥感图像稀疏重构的可行性，为压缩感知理论在遥感领域的进一步应用，以及遥感压缩成像系统的设计提供了实践基础。